I. INTRODUCCIÓN
Las bombas periféricas son máquinas rotodinámicas capaces de desarrollar, por medio de un único rodete, altas cabezas con caudales bajos. Este tipo de bombas incluyen un diseño compacto y la capacidad de funcionar con un npsh requerido bajo. Las bombas periféricas, así como las bombas centrífugas, son bombas cinéticas. La cabeza se alcanza gracias a la cantidad de movimiento proporcionada por el rodete al fluido, la cual se entrega primero como energía cinética, y se transforma después en energía de presión. A pesar de su baja eficiencia (por lo general menos del 50 %), las bombas periféricas pueden ser más atractivas que las centrífugas en algunas aplicaciones, debido a su bajo costo y alta cabeza. Se utilizan en aplicaciones de riego, en las que las grandes cabezas entregadas son necesarias cuando se recorren grandes distancias y los bajos caudales no representan un problema. Otra aplicación importante es el bombeo de agua potable en terrenos rurales, en donde la optimización de estas bombas genera un impacto positivo sobre sus costos de operación.
Hasta hace poco los modelos analíticos se utilizaron exclusivamente con el propósito de predecir las características de funcionamiento, y fueron limitados en representar el complejo campo de flujo dentro de la bomba que requiere una significativa corrección experimental. Actualmente, se implementan modelos que estudian las características de funcionamiento, en función del flujo particular que se presenta dentro de la carcasa.
En trabajos como el de Won Chul Choi et al. [1] se verificó de manera experimental que la cabeza y la eficiencia dependen fuertemente del ángulo de los álabes y su geometría. Esta situación se observó en modelos en los que no solo se puede evaluar su inclinación, sino también su trayectoria (curvos o rectos), además del espesor de los álabes. La geometría particular de los álabes en estas bombas da origen a un tipo de flujo que superpone un movimiento tangencial y un movimiento meridional. Este es un concepto adaptado de la meteorología, en la que se supone un patrón de movimiento norte-sur a lo largo de los álabes denominado “flujo toroidal”. Este movimiento es complejo de detallar mediante un análisis teórico debido a la separación del flujo en el ángulo de los álabes [2].En torno a la optimización en bombas rotodinámicas, Anagnostopoulos [3] desarrolló un algoritmo de optimización que se fundamenta en un gradiente sin restricciones que busca una geometría óptima para el rodete, el cual incluye el estudio de un conjunto de ángulos de los álabes para mejorar la eficiencia. Lo anterior sirve como guía para indicar que los parámetros influyentes en la optimización de este tipo de máquinas se enfocan en la geometría de los álabes y el tamaño del rodete. De esta manera, Meakhali y Park [4] proponen un modelo mejorado que maneja un ángulo de entrada y dos ángulos de salida a fin de lograr que la inclinación de los álabes cree un incremento en la cabeza obtenida; sin embargo, al manejar dos ángulos la ecuación a manipular tendrá un nivel de complejidad mayor.
También es posible abordar la optimización desde la perspectiva del punto de operación de la bomba. Hollemberg [5] formuló un modelo de optimización basado en la relación del número de Reynolds con el desempeño de la bomba, y encontró que al manejar Reynolds más altos se obtienen eficiencias más bajas. Otra forma de abordar el problema de optimización es por medio de un diseño robusto basado en herramientas de diseño estadístico. Bris [6] realizó la optimización de la desviación de la rata de flujo en una bomba reciprocante mediante un diseño robusto con factores geométricos, mecánicos y de condición del fluido de trabajo; a partir de esto genera las alternativas de solución al problema de optimización.
En las bombas periféricas el rodete está formado por una doble fila de álabes espaciados alrededor de su periferia, el cual se aloja en una voluta con un canal característico que facilita el flujo hacia la descarga [7], [8], tal como se ilustra en la Fig. 1.

Fuente: propia.
Figura 1 Partes de la carcasa y rodete de una bomba periférica: Succión, B. Descarga, C. Canal, D. Álabes
El fluido recorre internamente la carcasa que conecta el puerto de succión con el puerto de descarga, tal como se ilustra en la Fig. 2.

Fuente: propia.
Figura 2 La presión producida en una bomba periférica incrementa continuamente desde la succión hasta la descarga: A. Succión, B. Descarga. P. Presión, donde P4>P3>P2>P1
Al girar, el rodete golpea el fluido con los álabes; a causa de esta entrega de energía el fluido puede salir por el puerto de descarga [9]. En la Fig. 3 se resalta que la presión real a la descarga es el resultado de la energía cinética impartida en el rodete, la cual se transforma en energía de presión en la caja espiral, las aspas del rodete y el difusor, a lo que se restan las disipaciones de energía dentro de la voluta tales como la fricción y la recirculación del fluido, debido a la geometría de los álabes.
El desafío de mejorar la eficiencia hidráulica requiere un proceso de diseño inverso, en el cual un número significativo de diseños se deben evaluar. Esto conlleva a formulaciones complejas, numerosos experimentos y la necesidad de tener un software especializado para tal fin. Dado lo anterior, en la presente investigación se desarrolla una metodología que permite modelar el comportamiento de bombas periféricas basado en un desarrollo estadístico, con lo que se logra una formulación sencilla sin perder capacidad de predicción.
II. METODOLOGÍA
El modelo corregido para la curva característica en bombas periféricas se alcanzó con base en la metodología que se describe a continuación. Primero, se desarrolló un modelo a partir de la formulación propuesta por Euler para maquinas hidráulicas; luego, se realizó el montaje y la validación experimental en la cual se corroboró que este modelo presenta discrepancia con la curva real de la bomba. Se procedió entonces a realizar un análisis de las variables que más influencian el fenómeno, basándose en una completa revisión bibliográfica. Una vez se definieron las variables, se realizó un modelo estadístico de regresión con el fin de encontrar factores de corrección que ajusten el modelo al obtenido de manera experimental; obtenidos los factores de corrección, se realizó un análisis de significancia del modelo y, además, un análisis de los errores, en el que se comprobó que con la metodología desarrollada se mejoran de manera notable los resultados obtenidos.
III. FORMULACIÓN DEL MODELO
A. Descripción teórica
El comportamiento ideal de una bomba rotodinámica puede ser descrito con la ecuación de Euler, la cual depende solo de las características geométricas y las componentes de velocidad del fluido en contacto con el rodete. Primero, es necesario encontrar un ángulo beta de salida que, por ser recto, se supone igual al de entrada o muy cercano. Luego, es necesario suponer y validar que en el cálculo de la cabeza teórica no existe prerotación a la entrada, lo cual conlleva a que el triángulo de velocidades no tenga componente tangencial de entrada al rodete en dirección de acción del caudal (Fig. 5). Lo anterior conduce a que el ángulo beta a la entrada debe ser de 90°, debido a que el rodete es totalmente recto y perpendicular a la tangente del radio exterior.
En la Fig. 5 se ilustra el triángulo de velocidades a la salida del rodete. El ángulo beta para la salida se define al tomar en cuenta las tolerancias que se manejan en los procesos de manufactura en este tipo de bombas [10], la cual está del orden de +/- 1°. Se observa que se obtiene un valor asintótico cuando el ángulo beta a la salida es de 90°, lo cual conllevaría a una discontinuidad en el modelo, por lo que se define un ángulo de 89°, el cual está dentro del intervalo especificado por la tolerancia. El valor de 91° para la inclinación del álabe sería válido dentro del rango de tolerancias, pero solo es posible si el álabe está curvado hacia adelante, cuyo caso es solo funcional en ventiladores. Según Stepanoff [11], la ecuación de Euler está definida como:
Donde w es la velocidad de rotación del rodete [rad/s], g es la gravedad [m/s2], r el radio del rodete [m], b2 la altura del álabe a la salida del rodete [m], β2 es el ángulo de salida [°] y q es el caudal [m3/s].
Las características técnicas de la bomba analizada son las observadas en la Tabla 1, y su curva experimental se ilustra en la Fig. 6.
La curva de Euler de la Fig. 6 no representa el verdadero fenómeno físico, ya que no toma en cuenta ningún tipo de pérdidas en el rodete y la voluta. Además, está por debajo de la curva experimental de la bomba, lo que permite deducir que el flujo evaluado en ese instante por la ecuación está produciendo la cabeza descrita. También, las bombas periféricas acumulan flujo que recircula y permanece rotando dentro de los álabes, el cual luego se envía hacia la voluta, por lo que la cabeza teórica debe ajustarse al cuantificar los fenómenos descritos anteriormente. Es por esto que en la ecuación de Euler solo se evidencia el aporte del flujo de agua que entra e inmediatamente sale del rodete, mas no el que recircula en él. Basados en la formulación de Euler, se proponen dos factores de corrección desarrollados a continuación, uno para la cabeza máxima y otro para la pendiente de la curva, la cual para el caso de las bombas periféricas se asemeja a una línea recta.
Un análisis de flujo a la entrada y la salida de la bomba (succión y descarga) debería mostrar la diferencia de caudales, para lo cual se necesitaría un medidor de presión de vacío en la entrada y un manómetro a la salida, con el fin de determinar las presiones en estos puntos y realizar un análisis aplicando la ecuación de energía. Lo anterior esta por fuera del alcance del presente estudio, pero permitiría evidenciar analíticamente el fenómeno expuesto anteriormente.
B. Factor de corrección para la cabeza k H .
Debido a que la ecuación de Euler no satisface el comportamiento de la bomba real, es necesario establecer un factor de corrección para la cabeza máxima y cada bomba, el cual desplazará la curva a un valor de cabeza ideal que corresponda con la cabeza real. Se tomó una muestra de cinco bombas de esta familia con diferentes características, las cuales se ilustran en la Tabla 2. Con este conjunto de datos se realizó una regresión múltiple a fin de estudiar la relación de estos factores a partir de las variables diámetro (d) y revoluciones por minutos (rpm).
Con lo que se obtiene una expresión que corrige la cabeza máxima para la formulación de la ecuación basada en Euler:
Donde kH es el factor obtenido en el proceso de regresión, cuyos resultados se especifican en la Tabla 2. Para la bomba en estudio tenemos la siguiente ecuación:
El comportamiento de esta correlación corregida se observa en la Fig. 7.
C. Factor de corrección para la pendiente k A
El factor kA corregirá los valores de cabeza para cada caudal (pendiente de la curva). De esta manera, la ecuación resultante de aplicar ambas correcciones tendrá la capacidad de predecir el comportamiento de las bombas estudiadas mediante las variables relacionadas con cada factor en particular. Los datos obtenidos de las bombas analizadas anteriormente se relacionan en la Tabla 3. En este conjunto de datos se realizó una regresión múltiple con el fin de estudiar la relación de estos factores a partir de las variables diámetro (d) y altura del álabe a la salida del rodete (b2). La regresión se hizo para la variable (d) de primer orden y la variable (b2) con segundo orden, y se manejó un nivel de confianza del 95 %.
Con lo que se obtiene una expresión que corrige la cabeza máxima y los valores de cabeza para cada caudal basada en la ecuación de Euler:
Donde kA es el factor obtenido en el proceso de regresión, cuyos resultados se especifican en la Tabla 3. Para la bomba en estudio tenemos la siguiente ecuación:
El comportamiento de la correlación corregida se observa en la Fig. 8.
D. Verificación estadística
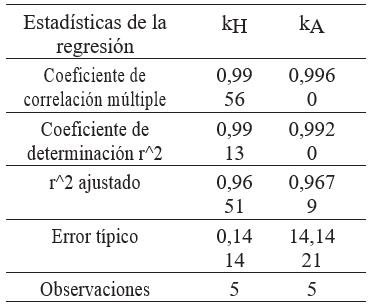
Se formula un análisis de regresión, de modo que se obtienen los resultados presentados en la Tabla 4.
Así, entonces, se valida la relación que existe entre los factores de corrección y las variables propuestas y, con base en los coeficientes de la Tabla 4, se concluye que al menos el 99 % de la variabilidad de los factores de corrección se explican a través de las variables de la regresión.
Las Fig. 9 y la Fig. 10 (curvas de regresión ajustada) muestran gráficamente la alta capacidad de predicción en la que todos los pronósticos para Y son bastante cercanos a los valores de Y. En los gráficos de residuales se observa la variabilidad de la muestra, lo que indica que se trabajaron datos a través de un rango abierto, y proporciona la confiabilidad de esta. Además, se resalta la variabilidad entre kA y kH, en los que, a pesar de esta, los coeficientes de correlación y predicción están por encima de 0,99, con una confianza del 95 %, de modo que indica una clara relación de las variables y su capacidad de describir el fenómeno con el modelo ajustado propuesto.
Se realiza una regresión al tomar los coeficientes presentados en la Tabla 5, de lo que se obtienen las ecuaciones para kH y kA respectivamente:
Tabla 5 Resultados de la regresión: coeficientes para la ecuación de predicción de factores de corrección

Fuente: propia.
La suposición de la influencia de las variables que se analizan es evidente en la expresión resultante. Las variables diámetro (d) y revoluciones por minuto (rpm) tienen influencia debido a que el volumen de líquido almacenado recirculando en rotación dependerá del tamaño del rodete (diámetro), y el tiempo que dure allí dependerá de la velocidad angular de este. También cabe resaltar la importancia de la altura del álabe a la salida del rodete (b2), ya que se relaciona con la cantidad de fluido al que el rodete le imparte energía en un tiempo determinado.
A partir de la expresión corregida de Euler, se hará una mejora de la potencia hidráulica basada en la obtención de una mayor cabeza manejando el mismo nivel de caudal. Lo anterior se logrará al realizar modificaciones geométricas en rangos establecidos de +/- 5 % para la altura del álabe y el diámetro en la curvade Euler. En la Fig. 11 y la Fig. 12 se observa la influencia del cambio en la geometría del rodete sobre la cabeza efectiva en la bomba.
IV. VALIDACIÓN EXPERIMENTAL
Para la validación experimental se realizó el montaje que se ilustra en la Fig. 13. A fin de construir la curva característica de la bomba, se estranguló el fluido con una válvula de bola, se midió la presión de salida a través de un manómetro digital calibrado (con resolución de 0,2 m de h2o) y el caudal con un medidor tipo Venturi.
Con la implementación de un diseño de experimentos se aleatorizaron las variables a analizar; al realizar las corridas en la instalación experimental se obtuvieron los resultados presentados en la Tabla 6.
Los resultados para los datos hidráulicos obtenidos de manera experimental se grafican en la Figura 14.
V. RESULTADOS Y DISCUSIÓN
Se realizaron variaciones para la geometría del rodete. El diámetro se varió por encima y por debajo del valor de referencia con el fin de observar el comportamiento de la cabeza de Euler. Con pequeñas variaciones en el diámetro (5 %) se obtuvo un aumento de cabeza media (para un caudal de 0,0003 m3/s) del 17,29 %, lo que implica que un pequeño cambio en el diámetro del rodete asegura una cabeza mucho mayor. Adicional a esto, se comprueba que, si se disminuye el diámetro, la cabeza obtenida decrece. Esta relación está dada por la fórmula propuesta por Euler, ya que el aumento del diámetro trae consigo un aumento de la velocidad tangencial, que para una bomba con salida radial es el principal aportante en la transmisión de energía.
Es necesario tener en cuenta que al aumento del diámetro aumenta la recirculación del fluido, debido a que tiene mayor espacio para recircular, lo cual ha sido comprobado en estudios como el de Hiroguchi et al. [9]. Cuando aumenta la recirculación disminuyen los gradientes de presión internos, lo que conlleva a que la cabeza efectiva sea mayor (véase la Fig.10). Lo anterior indica que la ecuación corregida propuesta en el presente trabajo puede describir y predecir el comportamiento de las bombas periféricas con un grado de exactitud apropiado.
Se verificó la influencia de la altura del álabe a la salida del rodete sobre la cabeza obtenida para distintos caudales. La influencia de esta variable fue de 3,3 % sobre la cabeza media, lo que se puede explicar -según Stepanoff [11]- ya que la altura del álabe está directamente ligada a un factor que depende de la variación del perfil de velocidad (debido a la fricción en este) a través de la altura del álabe a la salida del rodete, y que es directamente proporcional a esta. En comparación con el aumento dado en la cabeza media por el diámetro, el impacto de b2 no es tan significativo. Por otra parte, el resultado de combinar ambas variables (ancho y diámetro) aumentadas un 5 %, es un incremento en la cabeza media del 20,6 %, lo que entrega una relación de aproximadamente 4:1. Esto deja abierta las posibilidades de realizar trabajos futuros en torno a la optimización de la eficiencia total de este tipo de equipos.
Para el intervalo de análisis, la cabeza máxima obtenida experimentalmente fue de 20,59 m, y la cabeza máxima obtenida por la ecuación propuesta en este trabajo fue de 21,47 m, lo que supone un error del 4,22 %. Se observan errores, pero estos son de tipo aleatorios debido a que se tiene incertidumbre en la medición, además de factores como el tiempo de uso y ajustes mecánicos. Aun así, se valida estadísticamente que los errores en el modelo, comparados con los valores experimentales, son muy pequeños (un error típico del 1,34 %). Además, se realiza una evaluación del comportamiento de las medias y la varianza, en la que se asume que son iguales en el grupo de las cabezas experimentales y las cabezas predichas por el modelo, pues debería suponerse un comportamiento físico muy similar. Lo anterior se corrobora por medio de una prueba de hipótesis (Tabla 7 y Tabla 8) en la cual, para una confiabilidad del 95 % en una prueba de Fisher, el comportamiento de los datos para la cabeza real y la predicha por el modelo ajustado son iguales.
En la Fig. 15 se presenta una gráfica de los efectos del diámetro y la altura del álabe a la salida del rodete sobre la cabeza. La variable respuesta fue la cabeza media. Se realizaron combinaciones a diferentes niveles a fin de verificar la respuesta de la variable dependiente.

Fuente: propia.
Figura 15 Gráfica de efectos medios: Respuestas de la variable cabeza (m) para un caudal de 0,003 m3/s a los cambios de diámetro y b2. Realizado con MiniTab 17.
Como se observa, a fin de obtener una respuesta decabeza en el caudal intermedio lo más alta posible, las combinaciones deben realizarse de diámetro y b2 en sus niveles más altos, con lo que el aumento de estos en pequeñas proporciones (5 % según el presente estudio) tiene efectos significativos en la potencia hidráulica para un mismo caudal.
VI. CONCLUSIONES
Con el análisis desarrollado en el presente trabajo se evidenció cómo en las bombas periféricas existe una relación entre el diámetro del rodete, las revoluciones por minuto y un factor de corrección para la cabeza máxima que se ha denominado “KH”, la cual cuantifica el fenómeno de recirculación del fluido de trabajo en el rodete sin tener en cuenta otras formas de pérdida de presión en el rodete. También existe una relación entre el diámetro del rodete, la altura del álabe a la salida del rodete y un factor de corrección para las cabezas a los diferentes caudales que se ha denominado “KA”, el cual cuantifica las diferencias entre los flujos volumétricos de las bombas centrífugas y periféricas.
Se comprobaron los resultados obtenidos del modelo propuesto a través de validación experimental. Asimismo, se verificó que los pequeños incrementos en las variables geométricas (del 5 %) obtienen un incremento en la cabeza media de alrededor del 20 %, lo cual es una ganancia muy significativa. Este proceso de parametrización se puede mejorar aún más con el uso de CFD, lo cual deja abierta la posibilidad para desarrollar trabajos futuros.
Mediante la ecuación ajustada desarrollada en el presente trabajo se demostró que es posible obtener una cabeza más alta en una bomba al manejar un rango decaudal fijo, para lo cual es necesario variar parámetros geométricos. La cabeza máxima solo dependerá del diámetro del rodete, mientras que en las cabezas intermedias tiene una mayor influencia la combinación de la altura del álabe a la salida del rodete y el diámetro de este.