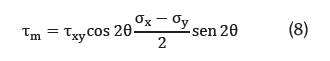INTRODUCCIÓN
En el suelo con determinado grado de saturación (inferior al 100 %) se requiere cierta fuerza para reducir el contenido de agua del mismo; este efecto se puede explicar mediante la succión. Esta tiene dos componentes: la capilar y la adsorbente, y está asociada a la capacidad de un suelo no saturado de absorber o retener el agua de sus poros y generar una tensión interna. La parte capilar depende de la distribución y tamaño de poro; la parte adsorbente está en función de la composición mineralógica de la parte sólida, así como también de la composición química del líquido [1], [2].
Este parámetro está compuesto de dos partes fundamentales: la succión mátrica (asociada a las fuerzas capilares que se generan entre la matriz del suelo y el agua) y la succión osmótica (la presión negativa por efecto de las sales disueltas en el agua). En ese contexto, la magnitud de la succión total corresponde al trabajo total de las fuerzas de capilaridad, absorción y ósmosis. Se ha estudiado experimentalmente el efecto de las componentes de la succión sobre el comportamiento del suelo, y se ha concluido que es representativa la influencia de la succión matricial sobre la respuesta deformacional y resistente del suelo, no siendo así el efecto de la succión osmótica [2]-[5].
La curva característica del suelo expresa la relación entre la cantidad de agua en el suelo y la succión. La cantidad de agua en el suelo generalmente se cuantifica en términos de humedad gravimétrica (w), grado de saturación (S) o humedad volumétrica. Para relacionar la succión y la humedad de equilibrio presente en los suelos se obtiene de la curva característica, que puede ser caracterizada a partir de las trayectorias típicas en secado o humedecimiento, entre las que aparece el fenómeno de la histéresis [2], [6]. En estudios realizados por Vanapalli [7] se reporta que la curva característica depende de varios factores, tales como la estructura del suelo, el contenido inicial de agua, la relación de vacíos, el tipo de suelo, la textura, la mineralogía, la historia tensional y el método de compactación. Adicionalmente, la curva característica se emplea para determinar otras propiedades, tales como la permeabilidad, la resistencia al corte y el comportamiento volumétrico de los suelos parcialmente saturados [8]. En la construcción de las cortinas de presas de tierra se emplean fundamentalmente suelos arcillosos con altos contenidos de finos, que presentan elevados valores de succión.
La definición conceptual de la resistencia al corte de un suelo (saturado o no) es la máxima resistencia por unidad de área que soporta el suelo a lo largo de un plano. En el caso de un medio saturado, la resistencia al corte se rige por el criterio de falla Mohr-Coulomb, que define la resistencia al corte por las variables ', y la variable de estado esfuerzo efectivo [2], [8], [9].
El objetivo de esta investigación fue analizar el comportamiento del factor de seguridad en presas de tierra al incluir directamente el ángulo de succión del suelo correspondiente a un grado de saturación determinado. La hipótesis planteada es que es posible obtener una variación del factor de seguridad con la incorporación del ángulo de succión en el análisis, que no difiere del comportamiento del suelo cuando se incorpora la curva característica en su totalidad. Igualmente, se plantea que es posible establecer una relación entre el ángulo de succión y el ángulo de fricción interna del suelo que se ajuste a las condiciones de los suelos arcillosos y al estado de carga que presente la presa en el momento del análisis.
BASES TEÓRICAS
La envolvente de falla extendida para los suelos parcialmente saturadas toma la forma matemática mostrada en la ecuación 1 [2], [10], [11]:
Donde
c': Cohesión efectiva.
φʹ: Ángulo de fricción interna efectivo.
φb: Ángulo definido por la rotación de incremento de esfuerzo normal respecto a la succión experimentada por el suelo.
En la ecuación 1 se observa que para los suelos parcialmente saturados, la relación de Mohr-Coulomb establecida ofrece la transición hacia la condición de saturación total. En este caso, la succión mátrica toma un valor igual a cero si la presión de poros debida al agua iguala a la presión de poros debida al aire, lo cual ocurre a medida que en el suelo se incrementa el grado de saturación [9].
Según [11], los parámetros de resistencia para los suelos parcialmente saturados se ven afectados por la influencia de la succión, y estos se pueden obtener a partir de los parámetros de resistencia del suelo saturado [1]. Igualmente, plantean que la relación existente entre y viene dada en función del parámetro de Bishop. Aplicando el criterio considerado por [1] se obtiene el ángulo de succión mediante la ecuación 2.
La envolvente de falla extendida de Mohr-Coulomb puede obtenerse en el plano, donde el parámetro φb se considera igual o menor que el ángulo Las presas de tierra son obras de ingeniería construidas para almacenar y distribuir las reservas de agua con el objetivo de obtener beneficios económicos y sociales [2]; siendo característico de estas la red de flujo que se genera en el interior del terraplén que funge como dique. Para referirse a la estabilidad de taludes se emplea el factor de seguridad (fs), obtenido a través de un análisis matemático de diversas variables, entre las que están involucradas la forma de la superficie de falla y las características de los suelos componentes del talud, entre otras. El valor del factor de seguridad se obtiene al realizar la comparación del esfuerzo cortante de falla con la resistencia cortante del suelo, en cualquier plano posible de falla del talud, y debe cumplir siempre como requisito, el ser mayor o igual al valor del factor que se establece por norma o se fija en proyecto [2].
Para obtener el fs mediante el empleo del Método de Elementos Finitos (mef) en el GeoStudio (2018) se establece la ecuación 3 .
Donde
Fr: Resistencia cortante total disponible.
Fm: Esfuerzo cortante total movilizado a lo largo de la superficie de falla.
Al dividir la masa deslizante en dovelas, se obtiene que la resistencia cortante total disponible de cada dovela se calcula multiplicando la resistencia a cortante del suelo en la base por su longitud. Por lo tanto, a partir de la forma modificada de la ecuación de Mohr-Coulomb para un suelo parcialmente saturado, la fuerza de resistencia disponible se muestra en la ecuación 4.
Donde
s : Fuerza de corte efectiva del suelo en la base de la dovela.
β: Longitud de la base de la dovela.
σn: Tensión normal en el centro de la base de la dovela.
El esfuerzo cortante total movilizado a lo largo de la superficie de falla de cada dovela se calcula multiplicando la tensión tangencial movilizada (τm) en la base de la dovela y la longitud de la base (ecuación 5), mientras que las fuerzas en los nodos (f) dependen de la matriz de interpolación de las funciones <N> y los valores de fuerza en los puntos de Gauss {F} (ecuación 6 ).
La fuerza normal resultante y la fuerza cortante movilizada se muestran en las ecuaciones 7 y 8. Ambas dependen de las fuerzas normales (σx; σy) y cortante (τxy) en la base de cada dovela, así como del ángulo positivo formado en el momento de aplicación de la carga (θ).
El paquete de programas recogidos dentro del GeoStudio 2018, comercializados por la empresa GeoSlope International Ltd., se basa en los diversos análisis que comprenden el suelo como componente fundamental. Es utilizado para el diseño y revisión de cimentaciones, análisis de estabilidad de presas, en la determinación de la red de flujo, estabilidad de taludes, terraplenes, entre otras estructuras. Este paquete presenta la posibilidad de calcular el factor de seguridad de taludes en presas de tierra a partir de la implementación del Método de Elementos Finitos [6]. En esta investigación se utilizan de forma acoplada dos de sus componentes: SEEP/W y SLOPE/W.
METODOLOGÍA PROPUESTA
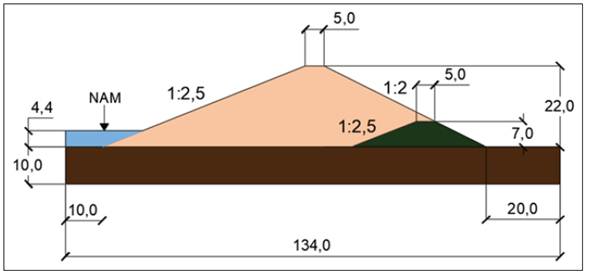
Tras una revisión de la base de datos del Instituto Nacional de Recursos Hidráulicos (INRH), el 69 % de las presas de tierra cubanas son homogéneas; de ellas, el 62 % presenta altura de cortina inferior a veintidós metros y cuyos procesos de construcción y mantenimiento se realizaron con base en la mecánica de suelos tradicional [6]. El modelo analizado es el de la presa de tierra mostrada en la figura 1.
Como material de cortina se usan dos tipos de suelos con clasificación CH (arcillas de alta compresibilidad), pero diferentes valores de sus parámetros físico-mecánicos (tabla 1). En la base se modelan tres suelos con clasificación SC (arena arcillosa). A partir de la combinación de los tipos de suelos en la cortina y la base se establecen relaciones entre el ángulo de succión y de la curva característica de suelo no saturado. La relación de permeabilidad establecida es kx = i2ky [2], [12].
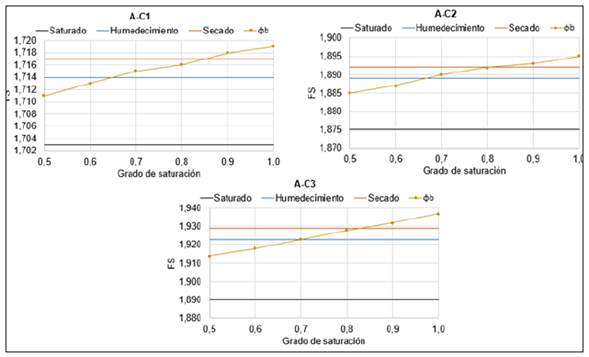
Los resultados de la curva característica correspondientes a los suelos empleados se muestran en la figura 2.
Para la obtención del ángulo de succión (φb), se ofrecen valores en un intervalo entre 50 y 100 % de grado de saturación, pues para menores valores de saturación se ob tienen succiones demasiado elevadas, que pocas veces se alcanzan en la naturaleza [13]. Los resultados correspondientes se muestran en la tabla 2, donde Sr es el grado de saturación.
Las tres bases estudiadas se tienen en cuenta considerando el estado de saturación to tal, mientras que el drenaje fue definido considerando que debe ser un material grueso con alta permeabilidad [14], [15]. La relación de permeabilidad establecida en todos los casos es unitaria [2]. Las propiedades correspondientes se muestran en la tabla 3.
Para los estados de operación y final de la construcción se emplearon los niveles de aguas normales (nan) o muertas (NAM), como se muestra en las figuras 3 y 4.
ANÁLISIS DE RESULTADOS
Para realizar el análisis utilizando el mef, se modela la estructura con la herramienta SEEP/W, donde se realiza la calibración de la malla que se va a emplear. Aunque la modelación tridimensional ofrece una representación más realista del problema en cuestión, para taludes con geometrías constantes y poco complejas un modelo bidimensional presenta resultados adecuados para el análisis de la estabilidad [16] factored based on the spacing distance, corresponds to extending anchors indefinitely in the third dimension. A three-dimensional (3D. Igualmente, se ha demostrado que el factor de seguridad crítico para el análisis tridimensional es más alto que el factor de seguridad bidimensional, independientemente de la estratigrafía y de la pendiente [17], [18].
El GeoStudio 2018 permite implementar varios tipos de elementos, dependiendo de la geometría del modelo en cuestión. Los resultados para la presa de tierra analizada se muestran en la figura 5.
En la figura 5 se observa que para elementos triangulares solamente, el incremento es superior al 50 % en todos los casos respecto a los resultados obtenidos al definir cuadrados y triángulos. Para analizar la variación del factor de seguridad en un punto con las variaciones de los tipos de elemento y de densidades de malla, se muestra la figura 6 [2].
En la figura 6 se observa que el FS disminuye al reducir la densidad del mallado. La variación es de 4 % para ambos tipos de elementos analizados, lo cual no resulta significativo [2]. A partir de una densidad de 0,6 metros, el FS no muestra variaciones; por lo tanto se selecciona una malla conformada por cuadrados y triángulos con una densidad de 0,6 metros.
El deslizamiento de taludes al final de la construcción tiene lugar en el talud aguas abajo y la presión de poros generada se debe al flujo de filtración establecido por el nam de la presa. Los resultados obtenidos en el GeoStudio se muestran en la figura 7.
El análisis del factor de seguridad se realiza en el SLOPE/W, trasladando los resultados del SEEP/W, considerando la curva característica experimental, el ángulo de succión (0b) y la curva de conductividad hidráulica.
Los resultados para el FS considerando las curvas características y de conductividad hidráulica para ambos suelos y las tres bases se muestran en la figura 8.

Fuente: elaboración propia
Figura 8 Resultados del estudio al final de la construcción. (a) Fs para el suelo A con ambas curvas. (b) FS para el suelo B con ambas curvas.
En las figuras 8 (a) y (b) no se observan diferencias entre los fs obtenidos para ninguno de los suelos empleando las curvas características y de conductividad hidráulica. Sin embargo, entre la rama en secado y la rama en humedecimiento existe una diferencia de hasta 5 % para el suelo A y 8 % para el suelo B. Entre el suelo saturado y parcialmente saturado se presenta una diferencia de hasta 10 % para el suelo A y 19 % para el suelo B. Este comportamiento se asocia a las restantes propiedades físicomecánicas de los suelos, como la cohesión y el ángulo de fricción interna. Adicionalmente, el fs aumenta si lo hacen las propiedades de la base; por lo tanto, para las combinaciones con la base tipo C1 se obtuvieron FS inferiores a las correspondientes con la base tipo C3, sin importar si el suelo de la cortina se encontraba saturado o parcialmente saturado.
El comportamiento del ángulo se succión en la etapa de final de la construcción para cada caso, comparando solo con el suelo saturado y la curva característica, se muestra en las figuras 9 y 10.

Fuente: elaboración propia
Figura 9 Comportamiento del FS considerando el ángulo se succión para el suelo A al final de la construcción.

Fuente: elaboración propia
Figura 10 Comportamiento del FS considerando el ángulo se succión para el suelo B al final de la construcción.
En las figuras 9 y 10 se observa que para el suelo A se obtienen valores de FS inferiores a los obtenidos con las curvas para los ángulos de succión considerados dentro del mismo rango. Mientras que para el suelo B los valores de FS dentro del rango ana lizado son superiores a los máximos alcanzados con las curvas características o las curvas de conductividad hidráulica.
Diversos autores [9], sugieren que el valor del ángulo de succión se fije como φb =1/2φʹ o φb = 1/2 φʹ en función del caso analizado. A partir de los resultados obtenidos para estos suelos, se sugiere de forma general φb = 0,7 φʹ que en los análisis al final de la construcción. Dado que cuando φb = φʹ se obtienen valores de factores de seguridad muy superiores a los obtenidos con las curvas características experimentales.
El análisis de la estabilidad de taludes en el estado de operación se considera en el talud aguas abajo y la presión de poros generada es debido al nan en la presa [2]. Los modelos correspondientes, empleando el GeoStudio 2018, se muestran en la figura 11.
Los resultados de los FS en operación, considerando las curvas características y la hidráulica para ambos suelos y las tres bases, aparecen en la figura 12.

Fuente: elaboración propia
Figura 12 Resultados del estudio en operación. (a) FS para el suelo A con ambas curvas. (b) FS para el suelo B con ambas curvas.
Las figuras 12 (a) y (b) presentan el mismo comportamiento que en las figuras 8 (a) y (b). Sin embargo, los incrementos son inferiores al 1 % entre ambas ramas de la curva característica, sin importar el tipo de suelo. Por otra parte, entre el suelo saturado y parcialmente saturado la variación es de hasta 2 % para el suelo A y hasta 4 % para el suelo B; lo que se explica por la presencia de la línea de corriente superior a una mayor altura dentro de la cortina de la presa, lo cual modifica el comportamiento del FS, reduciendo la influencia de las propiedades de los suelos no saturados. En el análisis del tipo de base, el comportamiento es el mismo que para el estado de final de la construcción.
El comportamiento del ángulo se succión en la etapa de final de la construcción para cada caso se muestra en las figuras 13 y 14.
Fuente: elaboración propia
Figura 13 Comportamiento del FS considerando el ángulo se succión para el suelo A en operación.

Fuente: elaboración propia
Figura 14 Comportamiento del FS considerando el ángulo se succión para el suelo B en operación.
En las figuras 13 y 14 se observa que para todos los suelos los valores de factor de seguridad dentro del rango analizado oscilan entre los valores de las curvas características o las curvas de conductividad hidráulica.
Varios autores [9], sugieren que el valor del ángulo de succión se fije como φb = φʹo φb = 1/2 φʹ en función del caso analizado. A partir de los resultados obtenidos para estos suelos, se sugiere de forma general que φb = 0,8 φʹ en los análisis en operación.
CONCLUSIONES
A partir de lo expuesto anteriormente es posible concluir que en el estado de final de construcción con el NAM, se observan incrementos del fs desde 7 hasta 20 % en los modelos estudiados, siendo el fs superior para todos los casos con la base tipo C3.
El incremento del fs en operación es inferior al 4 %. Por lo tanto, la posición de la línea de corriente superior y el nivel de llenado del embalse influyen de manera directa en el efecto de la succión en la estabilidad, sin importar el método mediante el cual se incluya en el análisis, pudiendo ser mediante la curva característica y la de conductividad hidráulica o con el uso del ángulo de fricción directamente.
Es posible utilizar el ángulo de succión como una constante, pero se recomienda que en el análisis de estabilidad al final de la construcción, el ángulo de succión se calcule empleando la relación φb = 0,7 φʹ, mientras que en el estado de operación se utilice la relación φb = 0,8 φʹ.