L. F. SARMIENTO R.^*1, C. C. PIEDRAHITA¹ and C. A. MONTAÑA R².

¹Ecopetrol -Instituto Colombiano del Petróleo, A.A. 4185 Bucaramanga, Santander, Colombia

²Numérica Ltda., Carrera 30 # 14-08 P. 3, Bucaramanga

^* To whom correspondence should be sent

ABSTRACT

In Colombia the areas of greatest petroleum exploration interest are characterized by complex structure with folds and thrust faults where it is important to estimate the thermal effects of faults to evaluate organic matter maturity and hydrocarbon generation processes. Except for a software model recently developed by the French Petroleum Institute (Francois Roure personal communication), current and public domain one dimension models do not consider lateral or downward heat flow, which are of normal occurrence in these areas, in addition such models assume instantaneous fault movement contrary to geologic observations. For balanced cross sections with (1) fault bend folds and (2) fault propagation folds we model heat conduction from the basement and organic matter maturity; outputs of the model are temperature and organic matter maturity at each point of the sections at different times while deformation is occurring. Boundary conditions are: absence of lateral heat flow on the lateral border of the sections, constant heat flow at the bottom of the sections, and constant temperature at the surface of the earth. The heat conduction equation applied to the sections was solved by the finite element numerical method with the ANSYS software. The obtained results for different deformation rates are shown and analyzed. Results show lateral variations of temperature and organic matter maturity. Contrary to one dimensional models, the steady state in two dimensions is reached faster, it is cooler and the temperature inversion is shorter. The less deformation rate the less thermal anomaly. At the topographic peaks temperature and maturity are lower than in the valleys. The fault propagation section presents a depth maturity inversion more pronounced than in the fault bend fold model. Depth maturity inversion intensity depends on the ratio between the deformation time T_d and the time passed just after deformation ceased T_p: T_d /T_p. If this ratio is greater the depth maturity inversion will be greater. This paper shows the possibility to determine the organic matter distribution in a structural section with a known thermal and deformation history.

Keywords: thrust fault, organic matter maturity, heat flow, fault bend fold, fault propagation fold.

RESUMEN

En Colombia actualmente las áreas de mayor interés en la exploración de petróleo están caracterizadas por estructuras complejas con pliegues y fallas de cabalgamiento, donde es importante estimar los efectos térmicos que éstas producen, para evaluar los procesos de madurez de la materia orgánica y de generación de hidrocarburos. Los modelos corrientes en una dimensión no consideran la posibilidad de flujo de calor lateral o vertical hacia abajo, que es de esperar en estas áreas, y suponen desplazamiento instantáneo de las fallas, situación que contradice las observaciones geológicas. En este trabajo se modelan los procesos de conducción del calor proveniente del basamento y de maduración de la materia orgánica para secciones estructurales balanceadas con pliegues formados por diferentes mecanismos: (1) pliegue por flexión de falla y (2) pliegue por propagación de falla. Como resultado se obtiene la temperatura y la distribución de la madurez a medida que transcurre la deformación en cada punto de las secciones. Las condiciones de frontera son: ausencia de flujo lateral de calor en los extremos de las secciones, flujo de calor constante en la base de las secciones, y temperatura constante en la superficie de la tierra. La ecuación de conducción del calor sobre el dominio de las secciones estructurales se resolvió usando el método numérico de elementos finitos, por medio del paquete ANSYS, donde se muestran y analizan los resultados obtenidos para diferentes velocidades de deformación. Los resultados muestran variaciones laterales de temperatura y madurez de la materia orgánica. A diferencia de los modelos en una dimensión, el estado estacionario en dos dimensiones se alcanza más rápidamente, es más frío que en una dimensión y la inversión de temperatura no dura tanto tiempo como en una dimensión. A menor velocidad de deformación menor es la anomalía térmica. En los picos topográficos, la temperatura y madurez son menores que en los valles. La sección con pliegue por propagación de falla presenta una inversión del gradiente de madurez con la profundidad más pronunciada que el modelo de pliegue por flexión de falla. La intensidad de la inversión de la madurez con la profundidad depende de la relación entre el tiempo de duración de la deformación T_d y el tiempo transcurrido después de la deformación T_p: T_d /T_p. Cuando esta relación es mayor, la inversión de madurez con la profundidad es más intensa. Este trabajo muestra la posibilidad de determinar la distribución de madurez de la materia orgánica en una sección estructural, con una historia térmica y de deformación conocida.

Palabras claves: falla de cabalgamiento, madurez de la materia orgánica, flujo de calor, pliegue por flexión de falla, pliegue por propagación de falla.

INTRODUCTION

Areas with thrust faults and related folding include major world petroleum reserves. However, due to their structural complexity they often constitute an exploration frontier. In the Andean countries major exploration areas are structurally complex with thrust faults (Carnevali, 1988; Cazier et al., 1995). As an example, current major exploration areas in Colombia are the Eastern Cordillera foothills (Cazier et al., 1995), the Eastern Cordillera, and the Upper Magdalena Valley. On these areas characterized by a complex structural geology it is important to evaluate with efficiency and detail the thermal perturbation effects produced by thrust faults to model and understand organic matter maturity and hydrocarbon generation processes, as well as the deformation kinematics and the resultant geometry of the structures favorable as petroleum traps.

Several authors have demonstrated both theoretically (Angevine and Turcote, 1983; Furlong and Edman, 1984; Lerche, 1990) and practically with real examples (Edman and Surdam, 1984; Nutten, 1984; Roure and Sassi, 1994) that the thermal effects on the organic matter maturity in thrust faulted areas sensibly differ from areas without thrust faults. If the emplacement of the thrust sheet is fast significant and abrupt, changes of the geothermal gradient will be produced. The bottom of the thrust sheet will be hotter than the rocks immediately below the fault, producing an inversion of the thermal gradient which differs from the monotonously increasing temperature normal gradient. (Angevine and Turcotte, 1983). Immediately after the thrust sheet emplacement heat is transported downward from the bottom of the hanging wall to the top of the foot wall rocks. After achieving thermal equilibrium, the depth thermal inversion disappears. This anomaly of the thermal gradient and the opposite to normal downward heat flow can be responsible for important thermal effects on organic matter maturity and hydrocarbon generation processes (Angevine and Turcotte, 1983). As an example the potential petroleum source rocks of the Villeta Formation in the Upper Magdalena Valley are immature in the hanging wall block while they are mature enough to generate hydrocarbons in the footwall block of the same thrust faults (Rangel et al., 1994). Thermal one dimensional modeling only assumes vertical heat flow and instantaneous displacement of thrust faults, which are conditions not occurring in nature. Oxbourgh and Turcote (1974), Brewer (1981), Furlong and Edman (1984), Edman and Surdam (1984), have studied the one dimensional problem, for example in one well, applying an analytical solution of the heat conduction equation (Carslaw and Jaeger, 1959). However, lateral effects near fault ramps need to be analyzed in two dimensions.

The objective of this paper is to model, using numerical techniques and the ANSYS software, heat conduction from the basement and organic matter maturity during deformation, in the 2-dimensional structural models of thrust faults and associated folds, knowing their geometry and deformation kinematics. Thermal effects produced by thrust faults in the popular models of fault bend fold (Suppe, 1983) and fault propagation fold (Suppe and Medwedeff, 1988) are modeled. The obtained results are analyzed to recognize and characterize thermal and organic matter maturity effects produced by thrust faults.

METHODOLOGY

To model heat conduction and organic matter maturation in structural sections representative of areas of thrusting and folding we applied the following methodology:

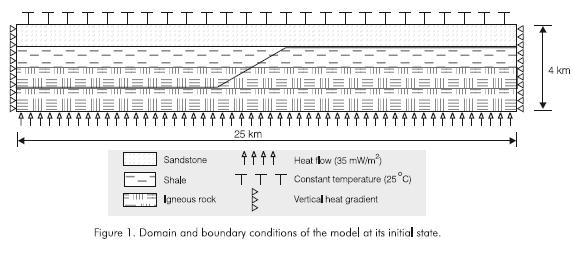
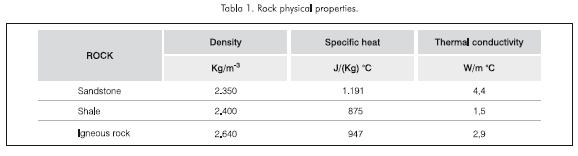
1. Selection and definition of a non deformed stratigraphic section (Figure 1), specifying its geometry, length, thickness, lithology of each rock layer and their thermal properties (Table 1).




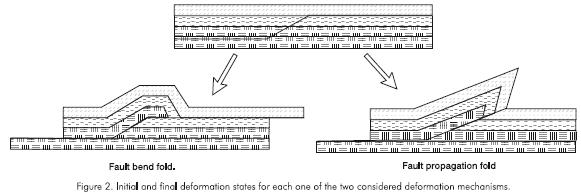
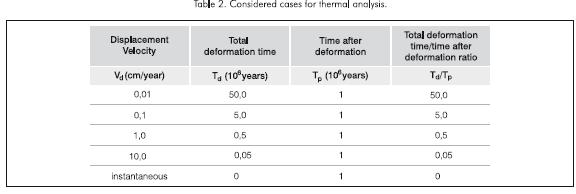
2. Geometric reconstruction of deformation kinematics using the structural balancing technique, in 6 progressive deformation states, from an initial non deformed state to a final deformed state for the fault bend fold (Figure 2) and fault propagation fold (Figure 2) structural models proposed by Suppe (1983) and Suppe and Mewedeff (1988). Velocity of displacement of the left border of the thrust sheet is constant in each model. Deformation states represent the state of the system at constant time intervals. A constant displacements of the left border of the thrust sheet of 1 km occurred during the interval passed between two successive de formation states. Table 2 shows 5 different displacement velocities of the thrust sheet left border that were considered for each model.




3. Heat transport numerical modeling, using the finite element method. Specification of the temperature at earth surface and heat flow from the earth interior and all other boundary conditions (Figure 1). The temperature distribution or temperature field was calculated for each deformation state for the 5 thrust sheet velocity cases above mentioned (Table 2) expecting to identify the rate of deformation effect on the temperature distribution and its evolution trough time

4. Calculation of the organic matter thermal maturity for each one of the studied cases, as a function of its time temperature evolution. In addition we calculated the organic matter maturity at each one of the deformation states for the 5 thrust sheet displacement velocity cases shown in Table 2.

5. Analysis of temperature and organic matter maturity modeled results.

HEAT TRANSPORT MODELING

In the studied problem heat is transported in two different ways:

-By thermal advection, related to matter displacement along the fault trajectory. The displacement of the fault places hot hanging wall rocks over cold foot wall rocks, and creates a depth temperature gradient inversion.

-By thermal conduction, as a result of the previous thermal disequilibrium. This tends to restore the thermal regime on the final geometry. Conduction heat transport is mathematically described by the following differential equation in the 2-dimension case (Carslaw and Jaeger, 1959), with heat sources (f) and without mass transport, isotropic materials, as the studied case (K: thermal conductivity, T: temperature at the point (x,y), C: specific heat, r: material density, t: time):

which is the equation we applied. Boundary conditions are: temperature at earth surface 25 °C (298,2 K), heat flow of 35 mW/m² from the earth interior and heat flow zero along the lateral boundaries of each modeled region (Figure 1). Equation was solved with the ANSYS software (Swanson Analysis Systems Inc., 1994) which is useful to model physical phenomena mathematically represented by differential equations. This software applies the finite element numerical method (Reddy, 1987).

ORGANIC MATTER MATURITY MODELING.

Using the time temperature evolution represented by the temperature distribution results for each one of the deformation states at different time, we calculated the organic matter thermal maturity one million years after deformation enting for the 5 thrust sheet displacement velocity cases given in Table 2. Organic matter maturity was calculated using the maturity integral, which represents the reaction rate integrated over time (Allen and Allen, 1990):

Where C: calculated organic matter maturity level, Co: original organic matter maturation at deposition time (t=0), A: frequency factor, a constant, Ea: activation energy, R: universal constant of gases, T: absolute temperature (K) and t: time. Because our interest was to study the effect of thrust deformation on organic matter maturation, we calculated and analyzed only the increase in organic matter maturation achieved during deformation without considering the original maturity level just before deformation.

We applied the average values for labil kerogen A = 1,58*10^-13 sec-1 and Ea = 208 KJul/mol taken from Mackenzie and Quigley (1988). Calculation was done to each model of the finite elements mesh using a program written in APDL language (ANSYS Parametric Design Language, Swanson Analysis System Inc., 1994). Since the results obtained using this equation are difficult to compare and interpret with commonly used maturity scales, as vitrinite reflectance, conversion of these values to the vitrinite reflectance scale was done calculating maturity of the non deformed section with equation (2) and with the approximate time temperature index (Waples, 1980) comparing the results to observe the equivalence and to finally convert these values to vitrinite reflectance using the equation:

found by Platte River Associates (1994), using correlation between TTI and vitrinite reflectance values presented by Waples (1985).

OBTAINED RESULTS

Temperature in the fault bend fold model.

Temperature distribution for this case is shown in Figure 3. In the non deformed state, temperature varies only vertically monotonously increasing with depth. The geothermal gradient is controlled by rock thermal properties. In the deformed states there are both lateral and vertical temperature variations. Assuming an instantaneous deformation just after deformation a depth temperature gradient inversion is produced below the fold near the fault ramp; this temperature distribution is the result of advection heat transport. After a long time, enough to reach thermal equilibrium, the temperature distribution is steady, the depth temperature gradient inversion disappears and a thermal anomaly remains in the fold region.

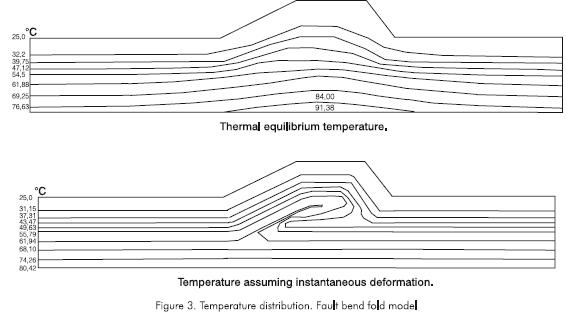
Figure 4 shows the time temperature variation after deformation at some selected points temperature is generally greater at the deeper points than in the shallower points. The footwall points are heated (more intense near the anticline fold), whereas the hangingwall points are cooled (more intense immediately above the fault). The studied model reaches thermal equilibrium after one million years. In contrast to one dimensional models (Oxbourgh and Turcote, 1974; Brewer, 1981; Furlong and Edman,1984; Edman and Surdam, 1984) the steady state in two dimensions is reached faster, it is cooler than in one dimension and the temperature inversion lasts less time than in the one dimension model.

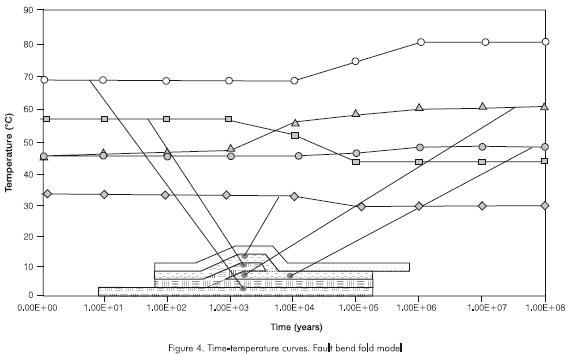
Temperature in the fault propagation fold model.

Temperature distribution in the fault propagation fold model is shown in Figure 5. Results of this case are similar to those of the fault bend fold model. The most significant difference is that immediately after deformation the depth temperature gradient inversion is more pronounced in the fault propagation fold model than in the fault bend fold model. In addition, the isotherms anomaly for thermal long after the ending of that deformation is more asymmetric in the fault propagation model. Temperature at the peaks or topographic convexities is lower than at the valleys or topographic concavities, although this effect was also observed in the fault bend fold model is more intense in the fault propagation fold model.

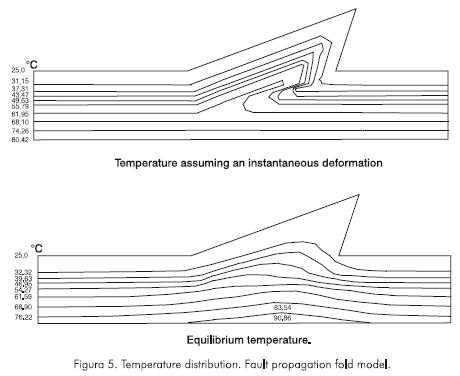
Figure 6 shows the time temperature variation for selected points of the model. As a general trend temperature is higher at deeper points. The footwall points are heated specially near the anticline fold, whe-reas they are cooled at the hangingwall points near the fold, this effect is more intense just above the fault. The studied model reaches thermal equilibrium after one million years. Contrary to one dimensional models (Oxbourgh and Turcote, 1974; Brewer, 1981; Furlong and Edman,1984; Edman and Surdam, 1984) the steady state in two dimensions in this case is also reached faster, it is cooler and the temperature inversion is shorter than in the one dimension model.

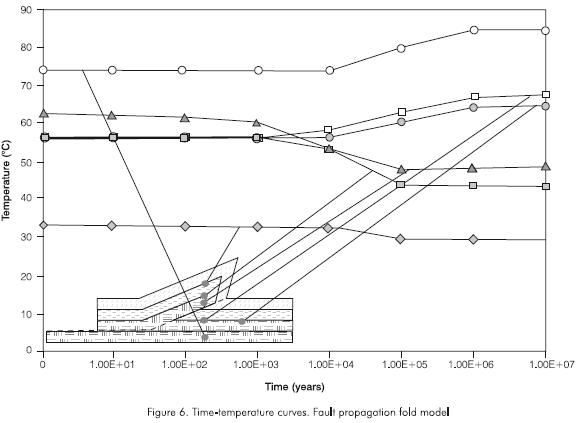
Organic matter maturity in the fault bend fold model.

The organic matter maturity distribution for the fault bend fold model at a 1cm/year deformation rate is shown in Figure 7. This figure shows both the vertical and lateral organic mater maturity variation, but in general maturity increases with depth. This increase is monotonous far away from the fold, but in the ramp zone below the fold, there is a depth maturity gradient inversion after deformation ending. On areas where the stratigraphic succession has been repeated by thrusting, maturity in the hangingwall block immediately above the fault is lower than maturity in the non deformed section, whereas maturity in the footwall rocks near the fault ramp is higher than far from the ramp in the same footwall block. As a general trend, maturity decreases with increasing deformation rate. On the external zone of the anticline fold isomaturity contours tend to follow bedding surfaces, however maturity is a little higher on the anticline backlimb than on the anticline forelimb (Figure 7).

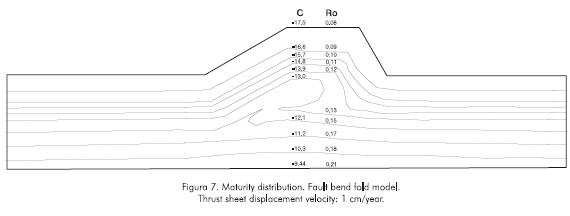
A high maturity is developed in the footwall just below the fault ramp and associated fold. Maturity gradually decreases from this high value with increasing distance from the ramp and from the region where rocks have been structurally repeated.

Topography has an effect on the organic matter maturity distribution. For the same rock layer maturity is lower at topographic peaks than far from the peaks due to a greater heat loss to the atmosphere. Maturity is higher at deep valleys than at other places of a same rock bed.

Figure 8 shows maturity variation with depth immediately after deformation ending for the fault bend fold model for different deformation velocities. Maturity values are higher in the fault ramp zone and associated fold (profile AB) than far from these structures (profile CD). In the region where the stratigraphic succession is not deformed or there is only slip movement along fault flats without structural repetition of rock beds, maturity increases with depth and the depth maturity variation is the same one obtained with the one dimensional modeling. The slope of the depth maturity curve, in the non deformed zone, is related to thermal conductivity rock layers. (the greater conductivity, the greater slope). Comparing maturity profiles for different times it is found, as expected, that maturity increases with time.. A depth maturity gradient inversion occurs in the fault ramp and associated fold zone which disappears far from these structures. Maturity acquired during deformation is lower for higher deformation rates.

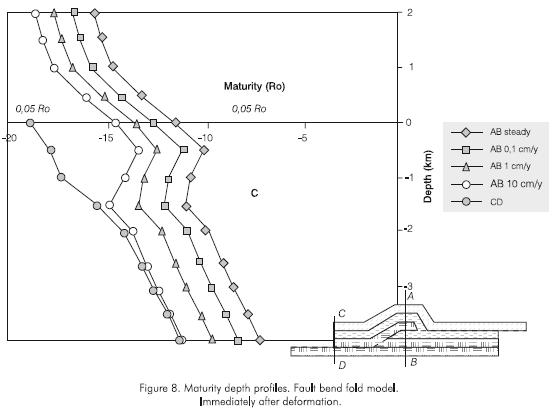
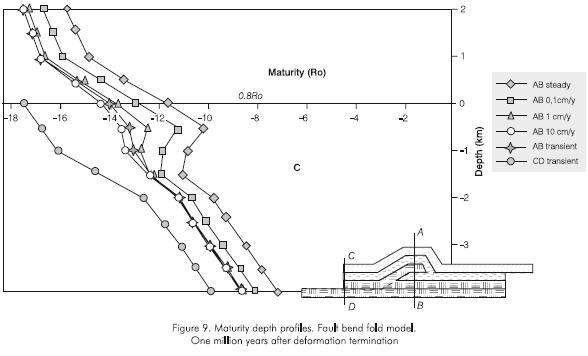
Figure 9 shows the depth maturity profiles one million years after deformation ending for the fault bend fold model. Results show higher maturity on the fault ramp zone and associated fold (profile AB) than far form these structures (profile CD). In the ramp and fold zone at higher deformation rate the maturity acquired during deformation is lower. In this more deformed zone, a depth maturity gradient inversion occurs when deformation rate is small, namely when the time interval during which the deformation occurred (T_d) is much longer than the time interval elapsed after deformation (T_p). Intensity of the depth maturity gradient inversion depends on the ratio between deformation time and time after deformation: T_d/T_p . A critical T_d/T_p value exists below which there is no depth maturity gradient inversion.

Organic matter maturity in the fault propagation fold model.

Figure 10 shows the organic matter maturity distribution at a 1 cm/year deformation rate for the fault propagation fold model. There are both vertical and lateral maturity variations. Maturity increases with depth, this increase is monotonous far from the fold, but in the fault ramp zone below the fold a depth maturity gradient inversion occurs after deformation ending, this inversion is more pronounced in this case than in the fault bend fold model. As a general trend at high deformation rate, lower maturity values.

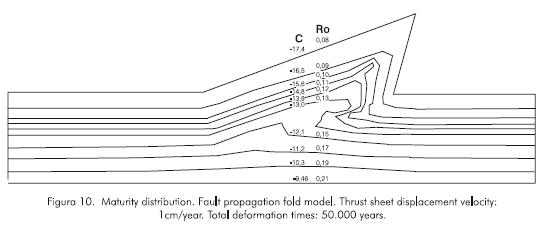
Depth maturity profiles immediately after deformation for the fault propagation fold model (Figure 11) show that maturity values are higher (profile AB) in the fault ramp and fold zone than far from these structures (profile CD). In addition a depth maturity gradient inversion, which disappears far from these structures, occurs in the fault ramp and fold zone,. This maturity gradient inversion is more intense in this model than in the fault bend fold model. At higher deformation rates lower increases of maturity during deformation.

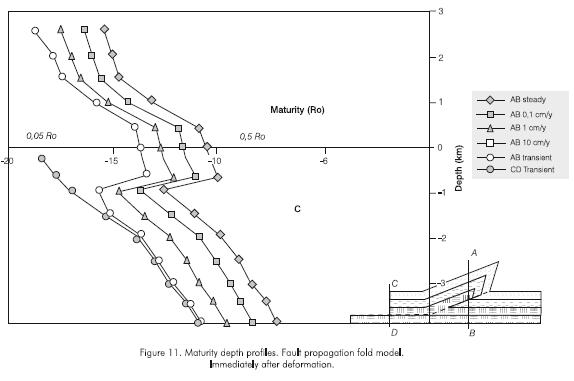
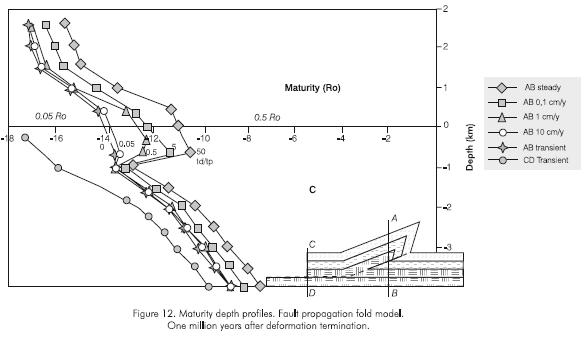
Figure 12 shows the depth maturity curves one million years after deformation ending for the fault propagation fold model. Except for the more intense depth maturity gradient inversion in the fault ramp and fold zone, the obtained results are similar to those of the fault bend fold model: maturity is higher in the fault ramp and fold zone (profile AB) than far from these structures (profile CD). In the fault ramp and fold zone there is a depth maturity gradient inversion when deformation rate is small, namely when the time interval during which deformation occurred (T_d) is long compared to the time interval after deformation (T_p). Intensity of the depth maturity gradient inversion depends on the ratio T_d/T_p between the deformation time interval (T_d) and the time interval after deformation (T_p). The critical T_d/T_p ratio value for no depth maturity gradient inversion is lower in this model than in the fault bend fold model. In the fault propagation fold, model maturity variation in the hangingwall block is more sensitive to time than the footwall block, where maturity variations are less dependent on time.

CONCLUSIONS

• Results show lateral variations of temperature and organic matter thermal maturity. Unlike the one dimensional models (Angevine and Turcote, 1983; Furlong and Edman, 1984), which assume instantaneous deformation, the steady state in two dimensions is reached faster, it is cooler than the one dimensional model and the depth temperature gradient inversion remains shorter than in the one dimensional model.

• Temperature distribution in the fault propagation fold model is similar to those of the fault bend fold model. The most significant difference is that immediately after deformation the depth temperature gradient inversion is more pronounced in the fault propagation fold model than in the fault bend fold model. In addition, the isothermal anomaly for thermal equilibrium elapsed a long time after deformation ending is more asymmetric in the fault propagation model.

• Maturity distribution is similar for the fault bend fold and the fault propagation fold models. The lower deformation rate, the lower thermal anomaly but the higher organic maturity level reached during deformation. At topographic peaks temperature and organic matter maturation is lower than at the valleys. The depth maturity gradient inversion of the fault propagation fold model is more intense than in the fault bend fold model.

• Intensity of the depth maturity gradient inversion depends on the ratio between the time interval during which deformation occurred T_d and the time interval passed after deformation stopped T_p: T_d/ T_p. The depth organic matter maturity gradient inversion increases with increasing T_d/T_p ratio. If T_d/T_p ratio is lower than a critical value there will not be inversion of the depth maturity gradient.

• This paper shows the possibility to predict organic matter maturity distribution of a structural cross section with a known thermal and deformation history. There is also a future possibility to use the model results in an inverse sense: inferring deformation kinematics knowing the thermal history and organic matter maturity.

ACKNOWLEDGMENTS

Francois Roure, Darío Barrero and Mario García for their helpful comments and improving ideas. María Teresa García-Herreros and the editorial committee of this journal also provided helpful suggestions.

REFERENCES

Allen, P. and Allen, J. R., 1990. Basin Analysis principles and applications, Blakcwell Scientific Publications, London , 451 p.        [ Links ]

Angevine, C. L., Turcote, D. L., 1983. "Oil generation in overthrusts belts", AAPG Bull., 67: 235 -241.        [ Links ]

Brewer, 1981. "Thermal effects of thrust faulting", Earth and Planetary Science Letters, 67: 235 -241.        [ Links ]

Carnevali, J. O., 1988. "El Furrial oil field, northwestern Venezuela: First giant in foreland and thrust belts of western Venezuela", AAPG Bull., 72: 78.        [ Links ]

Carslaw, H. S. and Jaeger, J. C., 1959. Conduction of heat in solids, Oxford Clarondon Press, 510 p.        [ Links ]

Cazier, E. C., Hayward, A. B., Espinosa, G., Velandia, J., Mugniot, J. F. and Lel, W. G. Jr., 1995, "Petroleum geology of the Cusiana field, Llanos Basin foothills, Colombia", AAPG Bull., 79 : 1.444 -1.463.        [ Links ]

Edman, J. D. and Surdam, R. C., 1984. "Influence of overthrusting on maturation of hydrocarbon in phosphoria Formation, Wyoming Idaho, Utah overthrust belt", AAPG Bull., 68: 1.803 -1.817.        [ Links ]

Furlong, K. P. and Edman, J. D., 1988. "Graphic approach to determination of hydrocarbon maturation in overthrust terrains", AAPG Bull., 68: 1.818 -1.824.        [ Links ]

Lerche, Y., 1990. Basin analysis, Quantitative methods, 1, Academic Press, Inc., San Diego, 562 p.        [ Links ]

Mackenzie, A. and Quigley, T. M., 1988. "Principles of geochemical prospect appraisal", AAPG Bull., 72: 399 -415.        [ Links ]

Nutten, M., 1984. "The functioning of petroleum systems in recently inverted zones", First Joint AAPG/AMPG Hedberg Research Conference, Geologic aspects of petroleum systems. Abstracts, 15 p.        [ Links ]

Oxbourgh, E. R. and Turcotte, R. L., 1974. "Thermal gradients and regional metamorphism in overthrust terrains with special reference to the eastern Alps", Schweizerische Mineralogische und Petrographische Mitteilungen, 54: 641 -662.        [ Links ]

Platte River Associates, INC., 1994. "BasinMod 1-D for UNIX/Motif, Basin Modeling System", Document Version 4.2. Denver, 395 p.        [ Links ]

Rangel, A. V., Giraldo, B. N. and Sarmiento, L. F., 1994. "Evaluación Geoquímica de la Cuenca del Valle Superior del Magdalena", Informe Final, Ecopetrol Instituto Colombiano del Petróleo, Piedecuesta, 195 p..        [ Links ]

Reddy, J. N., 1987. An introduction to the finite element method, Mac Graw Hill Book Company, New York, 495 p.        [ Links ]

Roure, F. and Sassi, W., 1994. "The functioning of petroleum systems in recently inverted zones", First Joint AAPG/ AMPG Hedberg research conference, Geologic aspects of petroleum systems, Abstracts, 25 p.        [ Links ]

Suppe, J., 1983. "Geometry and kinematics of fault bend folding", American Journal of Science, 283: 684 -721.        [ Links ]

Suppe, J. and Medwedeff D.A., 1988. "Fault propagation folding", Geol. Soc. Amer. Abstr. Prog., 16 : 670 p.        [ Links ]

Swanson Analysys Systems INC., 1994. Reference Manual ANSYS, Houston P.A., USA, 600 p.        [ Links ]

Waples, D. W.,1980. "Time and temperature in petroleum formation: application of Lopatin's method to petroleum exploration", AAPG Bull, 64: 916 -926.        [ Links ]

Waples, D. W., 1985. Geochemistry in Petroleum Exploration, International Human Resources Development Corporation, Boston, 232 p.        [ Links ]