English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
1 INTRODUCTION
Given modern society's high pollutant production, and its associated dramatic impact on life through phenomena such as greenhouse effect, acid rain, and climate change, Colombia has committed to reduce its greenhouse gas emissions by 20% in 2030 [1]. Therefore, it is necessary to shift towards renewable fuels with low environmental impact and highly efficient thermal technologies in the various sectors of the economy such as industry, transport, and residential, among others.
Progress requires an in-depth study of energy conversion using low emission fuels and, in turn, advanced stable and efficient combustion technologies, such as natural gas (NG) combustion, which produces less CO2 than both liquid and solid hydrocarbons, given the nature of NG and its bonded-carbons content. However, NG can be mixed with hydrogen (H2) in quantities that maintain the stability and safety of NG combustion to further reduce pollutant emissions due to the reduced carbon content, up to the elimination of CO2 . Similarly, it improves the combustibility of the mixture, and can extend the useful life of the NG reserves if the H2 is extracted from renewable sources through water electrolysis (green hydrogen) [2]. Currently, H2 can be obtained 100% from renewable sources using only surplus energy to drive Power to Gas systems, providing a feasible alternative associated with this fuel [3].
As a fuel, H2 implies great challenges in terms of storage, distribution, safety, and long-term environmental effects [2], [4], [5]. Due to the implicit disadvantages of H2, such as NOx emissions, fuel mixtures of H2 with hydrocarbons are a route to reducing greenhouse gas emissions. These mixtures have been evaluated for implementation in household burners, industrial burners, the automotive sector, and even in aviation [6-14].
Therefore, to achieve a decarbonization technology transition, the combustion properties of natural gas/hydrogen/air premixes must be studied, considering different atmospheric conditions with respect to altitude due to the effect of air pressure and density on combustion. At lower air densities, there is less oxygen availability, which affects combustion performance. This paper contributes to the state of the art by evaluating the performance of the following properties at the atmospheric pressure of Medellin, Colombia (1500 m.a.s.l.) with different equivalence ratios and hydrogen proportions: adiabatic flame temperature, laminar combustion velocity, ignition delay time, flame thickness, critical quenching diameter, and minimum ignition energy. Furthermore, theoretical properties related to energy availability and interchangeability are compiled for the different fuel blends.
2 STATE OF THE TECHNIQUE
Multiple studies report on the laminar burning velocity for a wide variety of fuels, including mixtures with hydrogen, for the reasons stated in the introduction. Echeverri-Uribe et al. [15] studied, numerically and experimentally, the effect of adding electrolysis products (H2/ O2 ratio 2/1) to methane on the laminar burning velocity and combustion stability. They found that an increase in the H2/O2 content increases the laminar burning velocity, while the thermal flame thickness decreases, concluding that the addition of electrolysis products to methane promotes hydrodynamic instabilities and decreases equidiffusive ones. They used the PREMIX subroutine of the Chemkin PRO software and the GRI-Mech 3.0 kinetic mechanism, finding the numerical results to correctly fit the experimental results at sub-atmospheric conditions.
Pareja et al. [16] analyzed, theoretically and experimentally, the laminar burning velocity of premixed hydrogen/air flames at low pressure, ambient temperature, and different equivalence ratios. In the experimental phase, the flame was generated using a slot-type nozzle burner (5mm x 13.8mm). Experimental observations were made using Schlieren photography. Numerical calculations were performed using the PREMIX one-dimensional premixed flame code from the Chemkin PRO package. For comparison purposes, the simulations considered the mechanisms proposed by Mueller et al. [17] and Li et al. [18], finding the Mueller mechanism a better fit to the experimental results.
On the other hand, Mishra and Dhiya [19] conducted an analytical study of the effect of hydrogen addition to different fuels (LPG, CH4, and acetylene) on the adiabatic flame temperature under rich, lean, and stoichiometric equivalence ratios. They found higher adiabatic flame temperatures with increasing proportions of hydrogen. Moreover, they developed a linear model for calculating the adiabatic flame temperature using the dissociation energy, the specific heats ratio, the C/H ratio, and the equivalence ratio.
Similarly, Hu et al. [20] studied, numerically and experimentally,laminar premixed methane-hydrogen-air flames at atmospheric conditions, finding that the laminar burning velocity increases as hydrogen is added to the mixture. They divided the dominant properties of the mixture as a function of three subgroups, depending on the proportion of hydrogen. Mixtures with less than 60% H2, achieved slightly superior properties as compared to 100% CH4, with linearly increasing laminar burning velocity. Subsequently, mixtures between 60-80% H2 were defined as a transition regime with exponentially increasing laminar burning velocity. Finally, mixtures with more than 80% H2 were defined as the inhibited methane regime, returning to linearly increasing laminar burning velocity. The numerical analysis was conducted using the GRI-Mech 3.0 mechanism, which captured the experimental trend for intermediate and low H2 content in CH4. The behavior of H2 in other hydrocarbons has been reported in the literature. Tang et al. [21] studied, numerically and experimentally, the laminar burning velocity and the combustion characteristics of premixed propane-hydrogen-air flames as a function of the equivalence ratio and the hydrogen content. They found results like those reported for NG or CH4, where increasing H2 content increases the laminar burning velocity, displaces the maximum laminar burning velocity towards richer mixtures, and decreases the thickness of the thermal flame. In addition, for H2 content below 60%, the properties of propane predominated.
Donohoe et al. [22] analyzed, experimentally and numerically, the ignition delay time and the laminar burning velocity for mixtures of natural gas and hydrogen at high pressures, parameterizing the premix temperature, the equivalence ratio, and the hydrogen content. Increases in preheat temperature, pressure, or hydrogen content resulted in a decreased ignition delay time. Similarly, the laminar burning velocity relates non-linearly to the hydrogen addition. Furthermore, the AramcoMech mechanism [13] was shown to approximate the experimental results quite well, with an error of 2% /ms.
Finally, Ren et al. [23] characterized numerically the properties of natural gas mixed with hydrogen, considering from 0 to 40% H2 content under different temperatures and initial pressures (298 and 500 K; 1 and 8 atm). The Chemkin PRO software showed that the adiabatic flame temperature and the laminar burning velocity increase as hydrogen is added to the mixture, due to the generation of H, O, and OH radicals that correlate with the burning velocity. Also, with the same equivalence ratio and hydrogen content, the adiabatic flame temperature and the burning velocity increase as the premix temperature is increased. On the contrary, increased pressure decreases the laminar burning velocity, while increasing the adiabatic flame temperature.
This analysis is a complement to the last work presented, evaluating and characterizing the properties of H2-NG combustion at 0.849 bar and greater H2 content.
Other properties, such as quenching diameter and minimum ignition energy, are predominantly studied experimentally in the literature. Therefore, this work is a comparative and complementary contribution through the numerical study of these variables. The results include an analysis of these properties and a comparison with those reported in the literature.
3 METHODOLOGY
MIXTURES ANALYZED
Combustion properties were evaluated for eight H2-NG fuel mixtures. The volumetric composition of natural gas (NG) distributed through the Sebastopol pipeline to the combustion laboratory of the University of Antioquia, Medellín (298 K and 0.849 bar) was taken from the TGI website [24], as shown in Table 1.
The fuels analyzed were 100% natural gas (NG), 100% hydrogen (H2), and mixtures of 15%-85%, 30%-70%, 45%-55%, 60%-40%, 75%-25%, and 90%-10% H2-NG, respectively. The results refer to the fuels by their volumetric percentage of hydrogen. For example, natural gas will be 0% H2, and 45% H2 indicates a mixture of 45% H2-55% NG. Fuel properties were calculated for stoichiometric conditions, while the combustion properties of the premix were evaluated from poor to rich mixing conditions, covering equivalence ratios from 0.5 to 1.5.
CALCULATION OF FUEL PROPERTIES
Through a stoichiometric balance, assuming complete combustion for an equivalence ratio of one, the following combustion properties were determined for each mixture: theoretical volume and mass of air, volume and mass of combustion products (wet and dry), theoretical volume and mass of CO2, theoretical volume and mass of H2O, flammability limits, specific gravity, heating values, Wobbe index, dew point, and CO2 emission factor. A detailed explanation of this procedure is shown in [25].
Flammability limits, specific gravity, heating values, and Wobbe index were calculated for each mixture as shown in equations ( 1 ), ( 2 ), ( 3 ), and ( 4 ), respectively.
In the equations, y . is the volumetric fraction of component i in the mixture, LII m is the lower flammability limit of the mixture, LSl m is the upper flammability limit of the mixture, d is the specific gravity, PC is the heating value, and W is the Wobbe index* of the mixture. *The Wobbe index is the ratio between the volumetric heating value of a gaseous fuel and the square root of its specific gravity. It is used to calculate how power is affected when a gas fuel is replaced by another.
The dew point is determined as the temperature corresponding to the partial water pressure in combustion products for saturated steam conditions. Accordingly, the vapor pressure is necessary, which depends on the volumetric fraction of the water in the combustion products, as calculated using equations ( 5 ) and ( 6 ).
Hence, saturated steam tables are required for obtaining the dew point. On the other hand, the calculated CO2 emissions indicate the degree of pollutant production with respect to the input power according to the fuel's heating value, as calculated using Equation ( 7 ).
CALCULATION OF COMBUSTION PROPERTIES IN PREMIXED FLAMES
The calculations of the premixed flame combustion properties, such as adiabatic flame temperature, laminar burning velocity, flame structure, and ignition delay time, were performed using the subroutines "Equilibrium", "Premix", and "Closed Homogeneus Batch Reactor" of the Chemkin PRO 18.2 software. Subsequently, calculations were combined with the equations listed in section 4.2.2. below, to simulate the properties of interest for adequate fuel control and thermal system design, such as flame thickness, critical quenching diameter, and minimum ignition energy.
KINETIC MECHANISM
According to [26], a kinetic mechanism is understood to be the set of steps that describe the decomposition of species in a reaction. A combustion mechanism may consist of only a couple of steps, general reactions, or thousands of elementary reactions. For example, the mechanism of Li et al. [18], commonly applied for hydrogen, contains 9 species and 21 steps, exemplifying a very compact mechanism as compared to mechanisms designed for hydrocarbons, which can consist of 57 species and 268 reaction kinetics such as the San Diego Mechanism (UCSD) [27], or 53 species and 325 reactions such as GRI-Mech 3.0 [28].
Consequently, the selection of a mechanism for the numerical characterization of combustion is an extremely complex and important issue, as the considered phenomenon can be over-or-underestimated. In works involving fluid dynamics, such as in [29], [30], and [31], simplified mechanisms such as Westbrook and Dryer or DRM19 are commonly used. On the contrary, works such as [15], [32], [33], and [34], whose simulations do not involve fluid dynamics but are interested in kinetic-chemical variables, use detailed mechanisms such as GRI-Mech 3.0 or UCSD. Therefore, as the present study focuses on kinetic-chemical variables, the GRI-Mech 3.0 mechanism is used to calculate the combustion properties of natural gas mixed with different proportions of hydrogen.
NUMERICAL METHODOLOGY
The adiabatic flame temperature was calculated using the Equilibrium model, with the temperature and pressure of the unburned gases at 298 K and 0.85 bar. The estimated flame temperature was set as 2000 K, with the volumetric composition of the fuel, the oxidizer, the equivalence ratio, and the combustion products assuming complete combustion. This simulation was processed for each of the eight mixtures, with the equivalence ratio covering from 0.5 to 1.5 in 0.1 increments.
The laminar burning velocity and flame structure of each of the mixtures were simulated using the Premix subroutine. The software's default profile was used for the initial temperature profile, and the multicomponent transport properties and thermal diffusivity were activated. The applied meshing conditions are shown in Table 2, with the equivalence ratio also covering from 0.5 to 1.5 in 0.1 increments.
Three continuation ranges were used to define how the computational domain is expanded during the simulation to find the convergence. The first continuation covers the range from 0 to 5 cm and the last one covers a broader domain from -2 to 10 cm, as shown in Table 3.
The ignition delay time was simulated with the Closed Homogeneous Batch Reactor subroutine, calculated under the maximum delta criterion generated for a species, in this case OH. The gas inlet temperature was used as the parameter to determine the variation in the delay time with preheat temperature, covering from 1000 K to 1600 K, in increments of 100 K. These results will be informative for some thermal applications such as diesel engines or mild combustion. Simulations were performed at three equivalence ratios, namely 0.5, 1, and 1.5.
Other properties, such as diffusive thickness, critical quenching diameter, and minimum ignition energy, were calculated using equations ( 8 ), ( 9 ), ( 10 ), and ( 11 ), which depend directly on the simulations conducted previously due to the variables involved.
The diffusive thickness was calculated as the ratio between the thermal diffusivity and the laminar burning velocity as shown in equation ( 8 ), taken from [35], and the thermal diffusivity with the calculation model of transport properties presented in [36].
Given low turbulence operation, according to Lefebvre's theory, the critical quenching distance (dc) was calculated using equation (9), assuming that the absolute turbulence intensity u' is equal to S L . The critical quenching diameter was calculated based on this distance and correlation ( 10 ) from [37].
Finally, the minimum ignition energy was calculated using equation ( 11 ).
4 RESULTS AND ANALYSIS
The properties of the fuel at stoichiometric conditions are shown in Table 4, which shows that less air is required for combustion as the hydrogen content of the mixture increases, thus reducing the volume of the combustion products. The theoretical volume of CO2 is also reduced, due to the reduced proportion of natural gas and, hence, carbons in the mixture, inhibiting the formation of carbon dioxide. The flammability range of hydrogen is quite broad, ranging from 4 to 75. Consequently, the addition of hydrogen to natural gas broadens the range of flammability as compared to pure natural gas, which is clearly evidenced in the results. As hydrogen is lighter than natural gas, its addition tends to decrease the specific gravity of the mixture. Although the volumetric heating value of hydrogen is lower than that of natural gas, its mass heating value is very high given its low density, and that is why hydrogen stores a large amount of energy from a mass perspective. Due to its low density, large volumes are required to store hydrogen in the quantities necessary to generate a given amount of energy.
From Table 4, the Wobbe index tends to decrease with increasing H2 content up to 75% H2, at which point the Wobbe index begins to increase. The Wobbe index is the ratio between the volumetric heating value and the square root of the specific gravity. Consequently, high concentrations of hydrogen decrease the growth rate of the volumetric higher heating value, while simultaneously decreasing that of the specific gravity. These two joint phenomena generate an increase in the Wobbe index in the range of 75 to 90% H2 in the mixture.
Due to the high volumetric fraction of water in the combustion products of high hydrogen content fuel mixtures, the partial pressure of the water in the combustion gases tends to increase.
This increases the dew point for saturated steam conditions, which means that the gases may begin their condensation process at higher temperatures for higher hydrogen content fuels.
The following presents the numerical results of Chemkin PRO simulations. The adiabatic flame temperature is shown in Figure 1, where eight fuel mixtures with different proportions of hydrogen are presented. The adiabatic flame temperature was calculated for equivalence ratios ranging from 0.5 to 1.5, to determine how such characteristic changes as a function of air availability at a pressure of 0.849 bar.
Figure 1 shows that the adiabatic flame temperature initially increases with the hydrogen content of the mixture, reaching a maximum at stoichiometry, after which it decreases more gradually. Chemically, this occurs because the bonds between H2 atoms are more difficult to break, releasing considerable energy when broken during combustion.
When the equivalence ratio is less than one, there is much air taking heat from the reaction. When the equivalence ratio is greater than one, there are resulting species that consume energy, although Figure 1 indicates that this is less than the heat taken away by air during lean combustion. The behavior of the adiabatic flame temperature follows the trend reported in the literature [19] [23].
Through simulation, laminar burning velocity (SJ values were obtained for the same mixtures. This property shows how fast a fuel is consumed or burned. As shown in Figure 2, the burning velocity of hydrogen is much higher than that of natural gas, and behaves in a different way at equivalence ratios greater than one. In addition, as hydrogen is added to the mixture, the point of maximum velocity shifts to the right. In other words, the maximum velocity occurs at higher equivalence ratios, approximately 1.5 according to the trend. These results agree with those found in [15], which analyzed lean and stoichiometric mixtures of water electrolysis products with up to 25% methane, with the burning rate increasing as the proportion of H2 and O2 increases, without exceeding 50 cm/s, as shown in Figure 2. This is consistent with the result shown in [23], finding the same maximum velocity for natural gas for equivalence ratios between 0.7 and 1.3. Similarly, [16] presents a laminar burning velocity analysis for pure H2 in lean, stoichiometric, and extremely rich mixtures (equivalence ratio up to 5), finding values around 200 cm/s for stoichiometric conditions and 250 cm/s for slightly rich mixtures. Finally, [38] presents SL for 30-70, 10-90, and 0-100% H2-CH4 mixtures, where SL increases to 48 cm/s for 30% H2 content, with a shift of the maximum velocity to an equivalence ratio of 1.1. These observations were performed at sea level conditions, showing a similar trend to that of operating at Medellín's conditions.
Figure 3 shows the flame structure for five of the eight mixtures analyzed at 3 different equivalence ratios: 0.8, 1, and 1.2. The behavior of certain species is shown as the position of the flame advance: H2, CH4, CO2 , and O2. The position range covers from 0.95 to 1.1 cm, as significant changes occur at this point, while remaining constant outside this range.
In all cases, CH4 and O2 decrease, which means that they are being consumed to carry out combustion. In addition, as the presence of hydrogen in the mixture increases, the initial concentration of methane decreases. The profile of CH4 indicates that its level drops to zero within this range, which means that it is consumed quickly, while the O2 level is still non-zero within the range, being consumed more slowly until reaching zero outside the range of the graph.
Hydrogen is present in all cases, even when pure natural gas is combusted, suggesting that hydrogen is generated in intermediate reactions. In addition, as the hydrogen content of the initial mixture is higher, its initial level increases. Oxygen exhibits similar behavior, although it is not entirely consumed in that range. Meanwhile, CO2 production is evidenced, initiating at a level of zero and increasing therefrom. Its final levels decrease with rising hydrogen content, until it stops appearing with pure H2, as there are no carbons present. As mentioned above, the same analysis was conducted at three equivalence ratios, finding the same trends in all situations. A higher equivalence ratio implies less air in the mixture, resulting in a lower molar fraction of O2 and, consequently, CO2 production. On the other hand, as the equivalence ratio increases, the fuel content of the mixture is higher, leading to higher mole fractions of H2 and CH4 for a rich mixture, in this case an equivalence ratio of 1.2.
The ignition delay time (IDT) was analyzed using preheat temperatures from 1000 to 1600 K at three equivalence ratios, specifically 0.5, 1, and 1.5, for each of the eight mixtures. Figure 4 shows the IDT, which decreases with increasing hydrogen content and with increasing preheat temperature. The more preheated mixture requires less energy to reach the ignition temperature, reducing the delay time. This behavior is also evident in [39], and it is the typical behavior found in the literature [40].
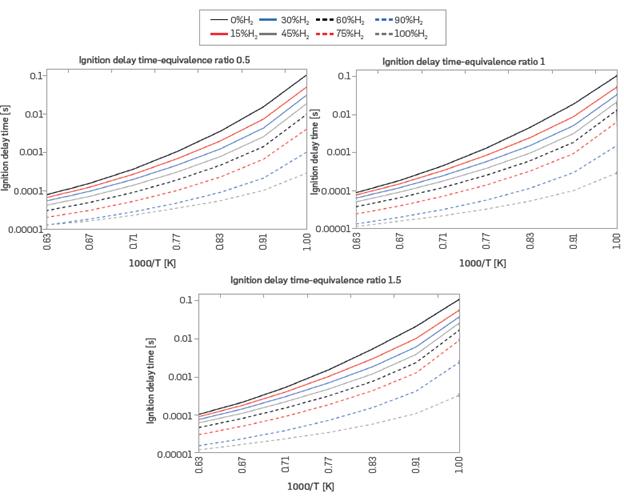
Figure 4 Ignition delay time for different mixtures of H2-NG and equivalence ratios (T = 298 K, P = 0.849 bar)
Furthermore, Figure 4 shows no significant dependence of the IDT on the equivalence ratio. However, IDT's sensitivity to the fuel mixture exhibits dependence on the preheat temperature. At the highest preheat temperatures, for any equivalence ratio, IDT ranges from 0.1 ms for pure NG to 0.01 ms for pure H2. At the lowest preheat temperatures, IDT ranges from 100 ms for pure NG, to 0.1 ms for pure H2. Therefore, at higher preheat temperatures, IDT varied by a single order of magnitude, while at lower preheat temperatures, IDT varied by three orders of magnitude. In other words, IDT shows greater sensitivity to increasing H2 content at lower preheat temperatures.
Figure 5 presents the diffusive flame thickness, which is the distance where there is mass transport from the inside of the flame to the flame front. The diffusive flame thickness decreases as the H2 content of the mixture increases, exhibiting inverse behavior to the laminar burning velocity, which explains the trend in the graph. The addition of H2 shortens the flame, implying that the global thickness and, therefore, the diffusive thickness, will be reduced. The trend is similar to the results obtained in [16], [21], and [41] for mixtures with H2. According to [15], the addition of H2 can increase hydrodynamic instabilities and decrease the equidiffusive ones due to the high diffusivity of H2, resulting in the wrinkled flames phenomenon.
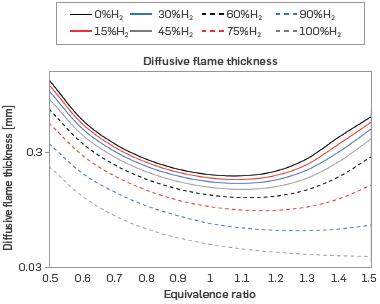
Figure 5 Diffusive thickness for different mixtures of H2-NG d equivalence ratios (T = 298 K, P = 0.849 bar)
The results of critical quenching diameter (CQD) are shown in Figure 6. The CQD decreases with increasing hydrogen content, as the CQD is directly proportional to the critical quenching distance which decreases with increasing laminar burning velocity. Thus, the behavior is inverted to that of SL, as seen in Figure 2. Similarly, the CQD minimum displaces towards rich conditions with increasing H2 content. Therefore, as the percentage of hydrogen in the mixture is increased, the CQD decreases.
It should be added that the literature does not present an exact constant for the calculation of this property using Eqs. 9 and 10 [42]. For example, [43] approximates it as twice the ratio of the thermal diffusivity to laminar burning velocity, while [25] multiplies the ratio by eight, and [44] multiplies by the square root of six. Furthermore, [45] parameterizes this constant under a series of considerations to solve the energy equation in the flame, resulting in multiplication factors of 4, 4.8, and 5.3. However, the CQDs shown in Figure 6 exhibit great similarity to the results reported in the literature for stoichiometric conditions [42], [46], and [47]. Crucially, observable differences may be attributable to the sub-atmospheric conditions in this work, which generate an implicit decrease in the laminar burning velocity and, therefore, the CQD.
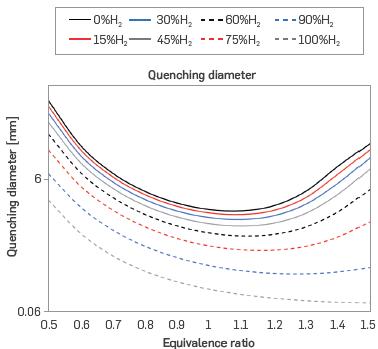
Figure 6 Critical quenching diameter for different mixtures of H2-NG and equivalence ratios (T = 298 K, P = 0.849 bar)
Figure 7 presents the minimum ignition energy (MIE), which behaves similarly to the CQD with both MIE and CQD decreasing with increased laminar burning velocity due to the facilitated ignition of a flame that burns faster depending on the nature and combustibility of the fuel. Consequently, the MIE tends to decrease with the addition of hydrogen to the mixture.
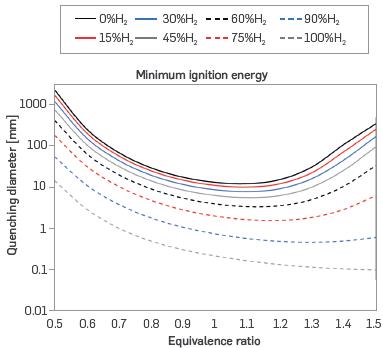
Figure 7 Minimum ignition energy for different mixtures of H2-NG and equivalence ratios (T = 298 K, P = 0.849 bar)
For mixtures from 0% to 60% H2, the MIE decreases with increasing equivalence ratio until reaching a minimum near or just beyond stoichiometry, and subsequently increases with richer mixtures. This turnaround point shifts to ever richer equivalence ratios as the H2 content of the mixture increases, resulting in a monotonically decreasing MIE for pure H2 over the considered equivalence ratio range from 0.5 to 1.5. As described in the literature, hydrogen has the same parabolic tendency as natural gas, but the minimum value of MIE is displaced to very rich conditions. Consequently, the MIE minimum for H2 lies outside the considered equivalence ratio range of 0.5 to 1.5, as can be seen in [41], [42], and [48].
In general, analyzing the results of the numerical calculations, combustion properties such as adiabatic flame temperature, laminar burning velocity, flame structure, ignition delay time, diffusive flame thickness, quenching diameter, and minimum ignition energy did not change significantly with the addition of hydrogen up to 45% by volume percentage, as the results curves remain quite close to the values associated with natural gas.
CONCLUSIONS
This work describes numerically the fuel properties of H2-NG mixture combustion at stoichiometric conditions. Furthermore, Chemkin PRO software was used to calculate the combustion properties of premixed flames at the atmospheric conditions of Medellín, Colombia, with a pressure of 0.849 bar and 298 K temperature at rich, poor, and stoichiometric equivalence ratios. The following presents the conclusions of this research:
Increasing hydrogen content enhances the flammability properties of the fuel, as well as the mass heating values. Furthermore, the adiabatic flame temperature increases with increasing hydrogen content in the mixture, which plays an important role in terms of energy availability. It should be noted that, given hydrogen's low density, its heating values in volumetric terms tend to be very low.
The addition of hydrogen to natural gas reduces CO2 emissions. According to the calculated emission factor, CO2 emissions are reduced by 17.54% for a 45% H2 content mixture. Furthermore, CO2 emissions are reduced by 70.17% for a 90% H2 content mixture and, finally, fully eliminated for the combustion of pure hydrogen due to carbon deficiency.
As the proportion of hydrogen in natural gas increases, the laminar burning velocity increases, which means that the reaction zone and, thus the flame thickness, decreases. Consequently, if hydrogen becomes an accepted fuel, more compact technologies are expected to avoid flame instabilities (flashback and blow off) to improve combustibility and generate efficient combustion with lower pollutant emissions.
This work's results are presented as a theoretical foundation for the development of thermal systems for the combustion of hydrogen-natural gas mixtures at sub-atmospheric conditions, since important safety variables, such as minimum ignition energy, ignition delay time, and critical quenching diameter, are sensitive to changes in fuel composition, equivalence ratio, and atmospheric conditions.
As the combustion properties of the natural gas-based mixture do not change significantly with up to 45% H2 content, the addition of hydrogen to natural gas in low concentrations is proposed as a viable step towards cleaner energy. The overall decreased carbon content of the mixture implies lower CO2 and CO emissions, allowing for the continued use of currently available and active thermal technologies while reducing greenhouse gas emissions.
Future work is recommended and expected to analyze different sub-atmospheric conditions to characterize and compile the properties required for guiding the design and adaptation of technologies to the altitude where the most thermal industrial cities using gaseous fuels are situated. Covering all cities worldwide is not feasible due to the excess computation required. Other models for heavy hydrocarbons and liquid fuels should be explored also to evaluate their viability when mixed with H2 under different atmospheric conditions.
