1. Introducción
La investigación en preparación de películas delgadas semiconductoras empleadas en la fabricación de dispositivos semiconductores requiere trabajar en técnicas de caracterización que permitan determinar propiedades ópticas, eléctricas y morfológicas de los materiales. Por ejemplo, en dispositivos fotovoltaicos uno de los parámetros más importante para determinar si los materiales sintetizados son adecuados para su uso son las constantes ópticas, a partir de ellas se puede establecer el grado de absorción de la radiación solar en la capa absorbente y si la brecha de energía prohibida es la que se necesita para absorberla. En la actualidad se usan celdas solares fabricadas con tecnologías de película delgada por ser más sencillas de fabricar y conllevar costos más bajos, estos dispositivos utilizan energía limpia y renovable que proviene del Sol para generar energía eléctrica mediante el efecto fotovoltaico. El mercado solar fotovoltaico que incluye todas las tecnologías de celdas solares es uno de los de mayor crecimiento y uso en los últimos años en energías renovables modernas y aporta al sector eléctrico mundial un total estimado de 760 GW 1.
Se han desarrollado métodos que permiten determinar las constantes ópticas en películas delgadas homogéneas, algunos requieren de la lectura del espectro de transmitancia, mientras que otros requieren del espectro de transmitancia y la reflectancia 2. R. Swanepoel desarrolló un método para determinar las constantes ópticas en películas delgadas homogéneas 3; luego, con el fin de realizar los análisis para películas delgadas semiconductoras no homogéneas desarrolló uno nuevo 4. Ambos permiten determinar las propiedades ópticas de las películas a partir de datos experimentales del espectro de transmitancia. Teniendo en cuenta que las películas delgadas semiconductoras pueden presentar variaciones en su composición y estructura bajo ciertas condiciones de preparación, desarrollamos un software para calcular constantes ópticas de películas no homogéneas, basado en el método de Swanepoel 4.
Actualmente existe un software llamado COPS desarrollado por nuestro grupo de investigación 5, el cual determina las constantes ópticas en películas delgadas a partir de medidas de transmitancia espectral; sin embargo, este software es adecuado sólo para ser usado en películas homogéneas. También hay aplicaciones como PARAV 6 y Refractor 7, el primero para calcular las constantes ópticas únicamente para películas homogéneas y el segundo para películas homogéneas y no homogéneas con una exactitud <= 2% 7, dichos softwares no presentan facilidad de obtención. Teniendo en cuenta que se han realizado trabajos en los cuales las películas sintetizadas no son homogéneas 8, surge la necesidad de crear una nueva aplicación a nuestro alcance que permita calcular estas constantes en películas tanto homogéneas, como no homogéneas. En este trabajo se desarrolla el software denominado COPS II (constantes ópticas en películas delgadas semiconductoras II) que puede ser usado tanto con películas homogéneas como no homogéneas, esto hace que la aplicación sea más integral. Además, maneja una tolerancia de 10-10, lo que permite tener aproximaciones más exactas.
2. Metodología
2.1 Teoría del cálculo de las constantes ópticas y espesor de las películas
La no homogeneidad en las películas tiene gran influencia en el espectro de transmisión óptica. Según Swanepoel 4 puede presentar una variación lineal en el espesor o algunas irregularidades en forma de rugosidad superficial. Las películas con índice de refracción 𝑛 son depositadas sobre un sustrato transparente, el cual presenta un índice de refracción 𝑠 y un espesor mayor al de la película, el grosor de la película delgada se expresa como:
donde: 𝑑 es el espesor de la película; 𝑑 es el espesor promedio; 𝛥𝑑 es la variación real en el espesor 𝑑.
Es posible transformar el espectro de una película no homogénea a homogénea manteniendo el espesor 𝑑; es decir, el 𝑑 de la película no homogénea es equivalente al 𝑑 de la película homogénea. Swanepoel 4 plantea las Ec. (2) y (3), las cuales relacionan las envolventes 𝑇´𝑀 y 𝑇´𝑚 de una película no homogénea con las envolventes 𝑇𝑀0 y 𝑇𝑚0 de una película homogénea, logrando así, un acople entre ellas.
para los máximos:
para los mínimos:
con
Los valores de los puntos 𝑇´𝑀 y 𝑇´𝑚 referentes a los máximos y mínimos del respectivamente, son obtenidos a partir de las medidas del espectro de transmitancia experimental de la película no homogénea. Con estos puntos se obtiene una curva envolvente tanto para los mínimos como para los máximos.
A partir de las Ec. (2) y (3) se calcula 𝑇𝑚0 y Ө en la región transparente. En esta región 𝑇𝑀0 es igual a 𝑇𝑠
siendo 𝑠 el índice de refracción del sustrato. Los valores de Ө son renombrados como Ө1.
Con el fin de extrapolar la información obtenida de la región transparente a la región de absorción, se traza
Para garantizar que se trabaja en la región transparente se descartan los puntos que presentan desviación ya que indican el inicio de la región de absorción 4.
donde:
Asimismo, el valor de Ө para cada par de puntos máximo y mínimo se calcula a partir de la Ec. (5). Luego, se calculan los valores de 𝑇𝑀0 y 𝑇𝑚0 con base en las Ec. (2) y (3), usando los valores de 𝑇´𝑀 y 𝑇´𝑚 y Ө calculados anteriormente.
Una vez realizada la transformación de la película, es posible calcular el 𝑑, el índice de refracción (𝑛(𝜆)) y el coeficiente de absorción (𝛼(𝜆)).
La ecuación que permite determinar la transmitancia 𝑇 en función de la longitud de onda 𝜆 y de los parámetros 𝛼, 𝑛, 𝑠 de una película delgada homogénea es 3:
donde:
La Ec. (7) a la Ec. (10) dependen de las siguientes ecuaciones:
A partir de los valores 𝑇𝑀0 y 𝑇𝑚0 se calcula el índice de refracción 𝑛, mediante la ecuación 4:
donde:
La Ec. (14) se usa para calcular el índice de refracción únicamente en los puntos del espectro donde existen máximos y mínimos.
Para el cálculo del espesor aproximado de la película homogénea, se grafica
con pendiente 2𝑑 y corte en el eje vertical de −𝑚1. Finalmente, se despeja 𝑑 4.
El error relativo reportado por Swanepoel para el índice de refracción usando la Ec. (14) y para el espesor aproximado 𝑑 usando la Ec. (16) es del 1%.
El coeficiente de absorción se calcula resolviendo la siguiente ecuación de forma iterativa 9:
donde 𝑇exp(𝜆) es obtenido a partir de los datos de transmitancia experimental del espectro, 𝑇cal(𝑘) es obtenido a través de la Ec. (6). La tolerancia es un parámetro variable, el cual se define según el caso.
Por otra parte, los materiales semiconductores utilizados en películas delgadas presentan generalmente un gap directo 10. El valor del gap es determinado usando la Ec. (18).
donde h es la constante de Planck, 𝛼 es el coeficiente de absorción, 𝐸𝑔 es el gap y 𝑣 es la frecuencia de la radiación. Se gráfica (𝛼ℎ𝑣)2 en función de ℎ𝑣, se traza una línea recta en la parte lineal de la curva y se toma el valor del corte con el eje horizontal.
2.2 Implementación de la aplicación
La aplicación tiene como objetivo calcular las constantes ópticas (CO): índice de refracción (n), coeficiente de absorción (α), brecha de energía prohibida (Eg) y espesor en películas delgadas usadas en celdas solares, tanto en películas homogéneas como no homogéneas. Para desarrollar la aplicación de software se utilizó el lenguaje de programación Python. Al ser Python un lenguaje interpretado, se obtienen scripts que pueden ser ejecutados en varios sistemas operativos, pero es necesario que en la máquina dónde se va a ejecutar el script se tenga el respectivo intérprete. En el caso de los sistemas operativos derivados de Unix (Linux y sus versiones), Python viene soportado e instalado en estos; y, para el caso de Windows, se cuenta con instaladores disponibles libremente.
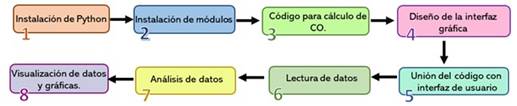
La aplicación tiene como datos básicos de entrada el espectro de transmitancia experimental de la película, para luego usar una metodología que incluye la aplicación de conceptos matemáticos que permiten realizar los cálculos y análisis de datos. En la Figura 1 se encuentra un esquema, en el cual se evidencia el proceso que se siguió para llevar a cabo la construcción del software.
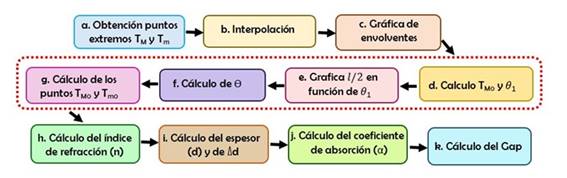
En cuanto a la realización del algoritmo para cálculo de las constantes ópticas, CO en la Figura 1, se utilizaron los pasos mostrados en la Figura 2. La obtención de los K extremos se hace mediante un procedimiento para hallar máximos (T M ) y mínimos (T m ) a partir de la gráfica de transmitancia. Estos puntos extremos alimentan un procedimiento de interpolación que calcula puntos complementarios; es decir, para cada punto máximo de la transmitancia se obtiene un mínimo correspondiente para el mismo valor 𝜆 (en nm), y viceversa. Con los valores y el proceso de interpolación se pueden obtener tanto para los máximos asociados a la envolvente superior T′ M como los mínimos asociados a la envolvente inferior T′ m , un par de vectores de tamaño K (paso c en la Figura 2).
Luego, usando los valores T′ M y T′ m calculados anteriormente, y con base en las Ec. (2, 3 y 4), se calculan los valores T m0 y de Ө en la región transparente Ө 1 . Después, a partir de la nube de puntos resultante de tomar los valores para cada punto extremo de Ө 1 versus l/2 (l/2 en función de Ө 1 ), se obtiene una pendiente y el punto de intersección con el eje vertical (m 1 ) con el fin reemplazar estos valores en la Ec. (5), la cual corresponde a la ecuación de la recta. Ello nos permite realizar el cálculo del valor de Ө. Con este valor, y con los valores de T′ M y T′ m obtenidos anteriormente, se determinan los valores de los puntos T M0 y T m0 utilizando las Ec. (2) y (3) (paso g. de la Figura 2).
En la tercera etapa se procede a calcular los valores del índice de refracción (n), el espesor (d) y su variación (∆d), el coeficiente de absorción y la brecha de energía prohibida (Eg). El cálculo del índice de refracción se obtiene utilizando la expresión en (14). Con el fin de calcular el espesor, primero se grafica l/2 en función de n/𝜆 reemplazando los valores de n obtenidos de la Ec. (14), para luego determinar la ecuación lineal de la misma. Segundo, se iguala el valor de la pendiente de la anterior recta a la expresión 2d y se despeja d. Si la película es no homogénea, es necesario calcular la variación real en el espesor Δd, para ello se despeja la variable ∆d y se reemplaza la pendiente hallada en la Ec. (16).
Una vez obtenido el índice de refracción y el espesor de la película, se realiza el cálculo del coeficiente de absorción usando la Ec. (17). Para ello se utiliza un método de optimización basado en el método de la bisección, que toma como función de costo la misma Ec. (17). Finalmente, para el cálculo de Eg, se gráfica (αhv) 2 en función de hv, se traza una línea recta en la parte lineal de la curva y se toma el valor del corte con el eje horizontal.
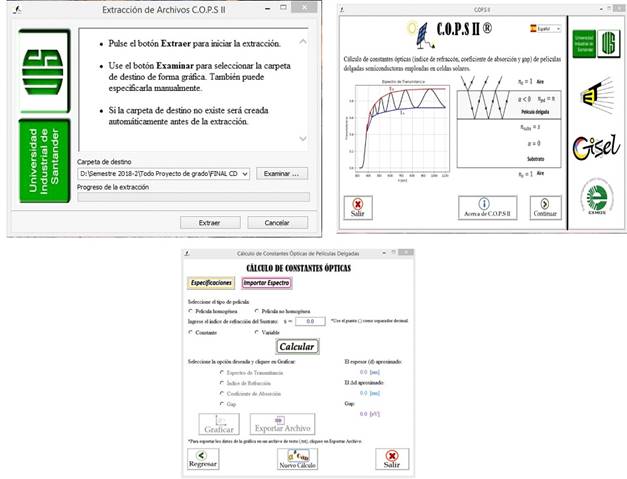
En particular, la aplicación fue diseñada en lenguaje de programación de Python, versión 3.6. Como premisa se tuvo en cuenta que fuera de fácil manejo y muy claro; por eso se cuenta con las especificaciones necesarias para ingresar los parámetros de entrada (ver Figura 3). La aplicación se lleva a un archivo ejecutable .exe; por lo tanto, tiene las mismas características de este tipo de archivos. Los recursos básicos del dispositivo en el cual se puede ejecutar son 4GB de RAM y procesador Intel CORE I3, pero se recomienda usar equipos con recursos superiores para obtener un mejor rendimiento en la ejecución del programa.
En la Figura 3 se presentan imágenes resultantes de la ejecución del aplicativo. Como se observa en la imagen el usuario puede seleccionar el tipo de película, es decir, si es homogénea o no homogénea, el índice de refracción del sustrato, si es constante o variable en función de la longitud de onda. Además, se pueden seleccionar las variables a visualizar, es decir, si desea observar las envolventes tomadas del espectro de transmitancia, los datos de índice de refracción, coeficiente de absorción y brecha de energía prohibida. La información se puede extraer en forma gráfica o de texto. Asimismo, se observan en la pantalla los datos de espesor y Eg determinados.
3. Resultados
Con el software desarrollado COPS II se calcularon las constantes ópticas y el espesor de películas delgadas no homogéneas fabricadas, para lo cual se reconstruyeron los espectros de películas delgadas semiconductoras no homogéneas, usando la siguiente expresión propuesta por Swanepoel 4.
donde:
Las Ec. (20) y (21) dependen de las Ec. (7-10) y (13).
En consecuencia, se realizaron simulaciones en Python partiendo de valores de constantes ópticas previamente calculadas, las cuales, al ser remplazadas en la Ec. (19), permiten reconstruir el espectro. Se tomaron los datos de dos espectros, uno estudiado por Swanepoel 4 y el otro por Caricato 11.
Con el objetivo de simular espectros reales y no ideales, se añadió a los espectros un ruido gaussiano aleatorio con media cero y desviación estándar de 0.0008; ya que el ruido está presente en la mayoría de las muestras experimentales. Aunque se realizaron varias simulaciones, solamente se presentan los resultados de la película de silicio amorfo hidrogenado (a-Si:H) presentada en el artículo de Swanepoel 4 debido a que se cuenta con la información necesaria para comparar los resultados, además este material semiconductor se usa para la fabricación de celdas solares obteniéndose eficiencias alrededor del 14% 12.
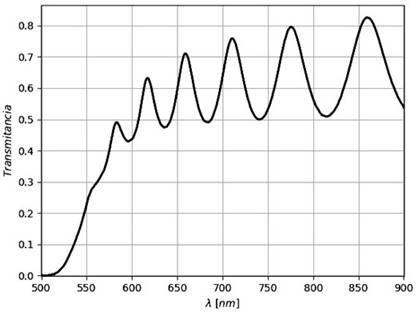
En la Figura 4 se muestra el espectro de transmitancia reconstruido de la película de silicio amorfo hidrogenado trabajada por Swanepoel. Al realizar la comparación con el espectro original 4, se observa la gran similitud que existe entre ellos. El error promedio encontrado al comparar los puntos extremos de los espectros es de 0.12 %, con base en los datos de la Tabla 1.
Tabla 1 Datos espectro experimental y simulado
| lambda (nm) | T-ref. 4 | T-Simulado | Error (%) |
|---|---|---|---|
| 859 | 0.826 | 0.827 | 0.144 |
| 814 | 0.509 | 0.509 | 0.056 |
| 775 | 0.796 | 0.797 | 0.195 |
| 740 | 0.5 | 0.499 | 0.125 |
| 710 | 0.759 | 0.759 | 0.044 |
| 683 | 0.491 | 0.490 | 0.190 |
| 658 | 0.71 | 0.708 | 0.201 |
| 636 | 0.474 | 0.473 | 0.087 |
| 616 | 0.631 | 0.631 | 0.045 |
| 598 | 0.432 | 0.432 | 0.076 |
| 581 | 0.484 | 0.484 | 0.048 |
| 566 | 0.32 | 0.319 | 0.239 |
| Error promedio | 0.121 |
Fuente: propia
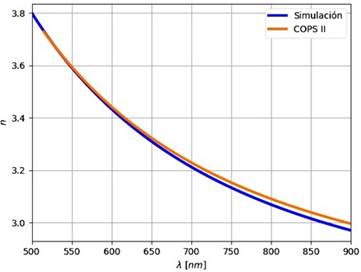
A continuación, se muestran las gráficas de las constantes ópticas simuladas a partir de ecuaciones y las gráficas obtenidas mediante el software COPS II para la película de a-Si:H. En la Figura 5, se representa la gráfica del índice de refracción obtenido mediante simulación con color azul y el calculado por COPS II con color naranja. Al comparar las gráficas se observa similitud entre ellas, el porcentaje de diferencia encontrado es de 0.4%, lo cual indica que el software es eficiente en cuanto al cálculo de esta constante.
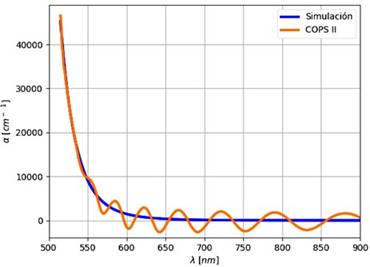
En la Figura 6, se observan las gráficas obtenidas por simulación y por el software COPS II del coeficiente de absorción, se representan con color azul y naranja respectivamente. Se obtiene un porcentaje de diferencia del 4.5%, el cual se debe al método numérico usado. Este, se basa en la iteración de los valores de coeficiente de extinción (𝑘), éste no es preciso para ciertos rangos de longitudes de onda, por lo tanto, las estimaciones dadas por el software presentan un pequeño error en el cálculo de esta constante, sin embargo, este error no afecta el análisis del coeficiente de absorción de la película.
Por otra parte, el software COPS II calcula un espesor de 1005.1 nm el cual, al ser comparado con el valor real de la película (1000 nm) presenta un porcentaje de diferencia del 0.51%. Con base en esto, se infiere que el software COPS II calcula valores confiables para el espesor de películas no homogéneas.
Finalmente, para el 𝛥𝑑 (variación en el espesor), el software arroja como resultado 32.31 nm que al ser comparado con el valor real de la película (30 nm) genera un porcentaje de error de 7.7%. Esta diferencia, se debe a los errores presentes en la determinación de los puntos 𝑇𝑀 y 𝑇𝑚 del espectro.
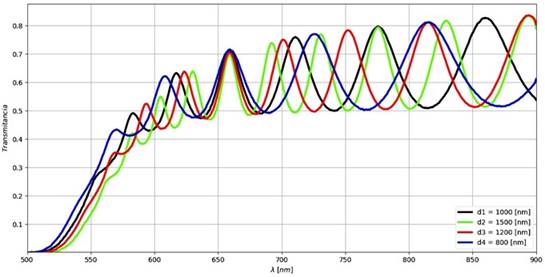
Una vez calculadas las constantes, se realizó un análisis del espectro para observar su comportamiento al presentar variaciones tanto en el espesor como en 𝛥𝑑. En la Figura 7, se muestra el espectro de transmitancia típico de una película delgada no homogénea de a-Si:H con variaciones en el espesor y 𝛥𝑑= 30 nm. En color negro se observa el espectro original con espesor de 1000 nm, al disminuirlo hasta 800 nm (línea azul) el número de franjas disminuye y al aumentarlo hasta 1500 nm (línea verde claro) el número de franjas aumenta.
Se observa que, están directamente relacionados ya que al variar el espesor de la película el número de franjas de interferencia que conforman al espectro de transmitancia también varía. Esto ocasiona que el espectro tenga más o menos puntos máximos y mínimos. Además, al variar el espesor cambia la brecha de energía prohibida Eg del semiconductor, esto se debe al tamaño de grano sobre la superficie de la película, el cual aumenta a medida que el espesor crece y esto hace que se produzca la disminución de Eg13.
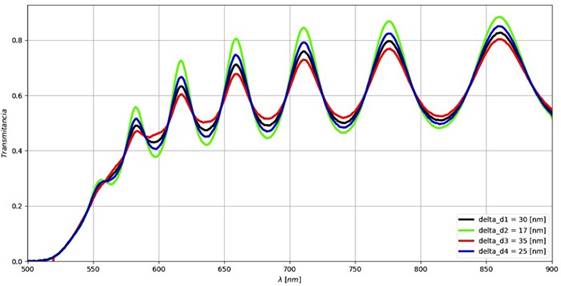
En la Figura 8 se observa el mismo espectro de transmitancia de la Figura 7, pero con variaciones en el 𝛥𝑑 y 𝑑= 1000 nm. En color negro se observa el espectro original cuyo 𝛥𝑑= 30 nm, al aumentarlo hasta 35 nm (línea roja) se observa que la amplitud de las franjas de interferencia disminuye y al disminuirlo hasta 17 nm (línea verde claro) la amplitud de las franjas aumenta. El 𝛥𝑑 indica que existen inhomogeneidades en la película, se observa que este es el responsable en el aumento o disminución de la amplitud de las franjas de interferencia del espectro de transmitancia.
4. Conclusiones
Se desarrolló el software COPS II para determinar las constantes ópticas en películas delgadas semiconductoras no homogéneas. Ingresando diferentes espectros típicos de transmitancia de películas homogéneas y no homogéneas, se encontró que el software presenta aproximaciones de las constantes ópticas con buena precisión con base en los porcentajes de diferencia calculados. En particular los resultados de la película de a-Si:H no homogénea que se estudió muestran que el error promedio encontrado al comparar los puntos extremos de los espectros es de 0.12 %, los espectros del índice de refracción obtenido mediante simulación y el calculado por COPS II son muy similares con un porcentaje de diferencia entre ellos de 0.4% y que en el coeficiente de absorción se obtuvo un porcentaje de diferencia del 4.5% entre el espectro simulado y el calculado. Esto indica que el software es eficiente en cuanto al cálculo de constantes ópticas. Además, el software COPS II calculó el espesor de la película con un porcentaje de diferencia del 0.51 %, siendo muy confiable para establecer el espesor de películas no homogéneas.
También se realizó un análisis del espectro de transmitancia para observar su comportamiento al presentarse variaciones en el espesor de las películas y en 𝛥𝑑, evidenciándose la relación directa entre el espesor y el número de franjas de interferencia en el espectro de transmitancia, y que 𝛥𝑑 es el responsable en la variación de la amplitud de las franjas de interferencia del espectro de transmitancia al existir inhomogeneidades en las películas.