Introducción
La formabilidad es la capacidad que tiene la lámina de metal para dejarse dar forma sin fallar o fracturar cuando es sometida a procesos de manufactura como el estirado y el embutido profundo 1,2,3. Este comportamiento puede estudiarse por medio de algunas propiedades mecánicas intrínsecas del material, entre las que están: la resistencia a tracción σu, el alargamiento total εt, el exponente de endurecimiento por deformación n, la anisotropía normal r y la anisotropía planar Δr. En este sentido, se encuentran trabajos como los realizados por Gedney. 4 y Casadiego et al. 2, que utilizan en su estudio las normas ASTM E8 5, ASTM E646 6 y ASTM E517 7 para caracterizar las láminas metálicas.
También existen ensayos simulativos que permiten determinar experimentalmente la formabilidad mediante la imitación, en cierta medida, de algunas condiciones de operación 8,9,10,11,12. Uno de los más utilizados en la actualidad es el ensayo para determinar las curvas límite de formabilidad (CLF) 13, que permiten hallar el rango de deformaciones máximas de la lámina a través de una prueba que simula el estirado biaxial y el embutido profundo. Este método ha sido utilizado para la caracterización experimental de diversos materiales como se puede apreciar en los trabajos realizados por Vadavadagi et al. 14, Safdarian et al. 15, Anand et al. 16, Pham et al. 17, Gauri et al. 18) y Kosuri et al. 19.
Tal como lo expone Barbosa et al. 1, esta prueba consiste en someter varias muestras de la lámina a embutido mediante un dispositivo compuesto por una matriz prensa chapa y un punzón hemisférico con las dimensiones estipuladas en la norma ASTM E2218 13, para luego medir las deformaciones y con ellas construir la curva.
Estas CLF son utilizadas para determinar qué tan cerca a la falla o al encuellamiento localizado puede estar una chapa durante una operación de conformado, o si una falla en particular es debida al procesado y/o a la pobre condición de la matriz o punzón, contribuyendo en la mejora de la productividad, tal como lo indica Cruz-González et al. 20.
Paul. 21, en su trabajo de revisión, muestra cómo a través de los años otros autores han desarrollado aproximaciones que permiten predecir con diferentes grados de precisión las CLF. Estas ecuaciones empíricas son función de algunas propiedades mecánicas del material y del espesor de la lámina. Como ejemplo, se presenta la predicción desarrollada por el mismo Paul. 21 descrita en Ec. (1), Ec. (2) y Ec. (3):
La Ec. (1) se utiliza para calcular el punto más bajo de la curva donde ocurre una condición de deformación plana FLD0 (Forming Limit Diagram cero) 9,12,13. Este se determina en función de la resistencia a tracción σu, el alargamiento total εt, el exponente de endurecimiento por deformación n, la anisotropía normal r, y el espesor de la lámina t.
Con la Ec. (2)y Ec. (3) se determina el lado derecho de la curva y, por último, la parte izquierda de la curva corresponde a una recta de pendiente -1.
En este trabajo se determinó experimentalmente la formabilidad de láminas de acero inoxidable AISI 304 utilizadas por la industria metalmecánica, principalmente a través de la construcción de las curvas límite de formabilidad en los 3 espesores seleccionados para el estudio. Este material pertenece a la familia de los aceros inoxidables austeníticos, que son los más dúctiles y de mejor formabilidad, con aplicaciones como equipos para procesamiento de alimentos y equipos de procesos químicos y hospitales 10. Estos datos técnicos permitirán a los fabricantes de este tipo de materiales predecir el comportamiento en los procesos de estirado y embutido.
Metodología
El material objeto de estudio son láminas de acero inoxidable adquiridas en el comercio y utilizadas por el sector metalmecánico, en calibres 16, 18 y 20 (1.5, 1.2 y 0.9 mm respectivamente). El análisis químico realizado por Barbosa et al. 22) confirma que los componentes están dentro del rango estipulado para este acero, y de acuerdo al bajo contenido de carbono, las chapas se pueden considerar como grado 304L con características de mejor soldabilidad.
En cuanto a las propiedades intrínsecas, la Tabla 1 recoge algunos datos promedio del trabajo realizado por Barbosa et al. 22 para cada uno de los espesores.
Tabla 1 Propiedades mecánicas de los aceros en estudio.
| Gauge | Tensile strength (σu) MPa | Yield strength (σy) MPa | Total elongation in 50 mm gauge length (εt) % | Strain-Hardening Exponents n | Normal anisotropy r | Planar anisotropy Δr |
|---|---|---|---|---|---|---|
| 16 (1.5 mm) | 666 | 286 | 0.57 | 0.378 | 1.05 | -0.19 |
| 18 (1.2 mm) | 601 | 251 | 0.58 | 0.371 | 0.99 | -0.15 |
| 20 (0,9 mm) | 530 | 253 | 0.63 | 0.393 | 0.93 | -0.11 |
Fuente: Elaboración propia
El método a seguir para determinar las curvas límite de formabilidad fue el especificado por la norma ASTM E 2218 “Standard Test Method for Determining Forming Limit Curves” 13.
Para cada espesor, se fabricaron 8 probetas de 200 mm de largo con anchuras centrales que van desde 25 hasta 200 mm con incrementos de 25 mm, Figura 1. Sobre éstas se construyó un patrón de círculos de 2.5 mm de diámetro con separación entre ellos de 1 mm, mediante grabado láser en una máquina Marca Bodor, Referencia ML20F Gold, con una potencia de 30W, Figura 2.
Las pruebas se realizaron en una máquina universal de tracción/compresión marca IBERTEST, modelo IBMT2-600, a la cual se le adaptó un dispositivo con los detalles geométricos y dimensiones estipulados en la norma ASTM E2218 13, y para lo que se requirieron algunos elementos de acople, tal como se muestra en la Figura 3. Las láminas para cada espesor fueron deformadas hasta la falla tal como se muestra en la Figura 4.

Fuente: Elaboración propia
Figura 1 Geometría de las 8 probetas maquinadas por cada espesor para las pruebas de las curvas límite de formabilidad CLF.

Fuente: Elaboración propia
Figura 2 a) Patrón utilizado. b) Montaje y grabado láser de las probetas.

Fuente: Elaboración propia
Figura 3 Dispositivo para el ensayo de determinación de las CLF, con sus elementos de acople a la maquina universal IBERTEST, modelo IBMT2-600.

Fuente: Elaboración propia
Figura 4 Probetas después del ensayo para determinar las curvas límite de formabilidad.
Posteriormente, con el uso de un estereomicroscopio digital marca MOTIC modelo DM143-N2GG-B, conectado a un PC mediante el software Motic Images Plus 3.0 ML se realizaron las mediciones necesarias para la construcción de las CLF. Inicialmente, se tomaron las medidas del diámetro interno de los círculos sobre las láminas antes del ensayo para tener la referencia sobre la cual determinar los porcentajes de deformación posterior. Al final del ensayo, se realizó una clasificación visual al patrón de círculos que se convirtieron en elipses, clasificándolas de acuerdo a su estado como:
Buenas: elipses que están en la zona de encuellamiento no localizado.
Marginales: elipses que están en las zonas donde hubo un adelgazamiento pronunciado de la lámina (encuellamiento localizado).
Fracturadas: elipses ubicadas en zonas donde la lámina sufrió rotura.
En el proceso de conformado de la lámina el encuellamiento difuso o no localizado ocurre normalmente después de la deformación uniforme a partir del esfuerzo máximo (capacidad de carga máxima del material), seguidamente la deformación es localizada solo en el área de encuellamiento, y finalmente llega la fractura 21
En las elipses seleccionadas se midió la longitud de los ejes mayor y menor, y con ellas se determinaron los porcentajes de deformación correspondientes e1 y e2, de acuerdo a las Ec. (4) y Ec. (5), como se muestra en la Figura 5.
En donde:
W o y L o equivalen al diámetro inicial de los círculos y se puede observar que, si bien la deformación mayor siempre es positiva (𝑒1), la menor deformación puede ser positiva, negativa o cero (𝑒2) 10.
Posteriormente, se determinan los valores de las deformaciones reales en el eje mayor ε1 y el eje menor ε2 mediante las Ec. (6) y Ec. (7).
Los valores de deformación real calculados se llevaron a un diagrama 𝜀1 vs 𝜀2 para trazar la curva límite de formabilidad. En la elaboración de los diagramas se tuvieron en cuenta las siguientes condiciones: cada punto fue identificado como bueno, marginal o fracturado mediante una simbología, como se muestra en las Figuras 7, 8, 9 y 10. En todos los casos, el rango de la deformación 𝜀1, se tomará entre 0 y 0,8, y el de 𝜀2, se tomará entre -0,4 y +0,3.
Resultados y discusión
El análisis metalográfico de las muestras de las chapas de los 3 calibres presenta la misma microestructura, con austenita como única fase con granos entre 15 y 20 micras (tamaño de grano austenítico ASTM entre 4 y 5), y la presencia de maclas 22. En trabajos previos realizados para aplicaciones relacionadas con procesos de conformado de lámina, se menciona que es preferible un tamaño de grano austenítico ASTM de 7 10. En la Figura 6 se puede apreciar a manera de ejemplo la micrografía de la chapa de calibre 16 a 500 aumentos (ataque: HCl y H2O2).

Fuente: Elaboración propia
Figura 6 Micrografía de una muestra de la chapa de calibre 16. La microestructura muestra austenita como única fase. Las 3 chapas muestran la misma microestructura.
En las Figuras 7, 8 y 9 se presentan las curvas límite de formabilidad para los 3 espesores de lámina. Estas fueron trazadas en la vecindad entre los puntos buenos y marginales, tal como lo describe en sus ejemplos la norma ASTM E2218 13.
Para los 3 casos la parte izquierda de la curva a partir de 0 de deformación real 𝜀2, corresponde a una semirecta con pendiente pronunciada y representa los puntos medidos sobre las probetas de 25 hasta 125 mm de ancho. En estas probetas las deformaciones reales menores 𝜀2 son negativas y simulan el comportamiento en un proceso de embutido 10.
Por otro lado, la parte derecha de las CLF tiene de manera general, forma de una curva polinomial, y agrupa los puntos medidos en las probetas desde 150 hasta 200 mm de ancho. Allí, las deformaciones reales menores 𝜀2 son positivas y las probetas simulan el comportamiento de la lámina en procesos de estirado. Por último, la tendencia es a que los tramos derecho e izquierdo de la CLF se unan en el punto más bajo de la misma, cuya deformación real menor de 𝜀2 se encuentra en el rango de 0 a 0,05, condición de deformación plana denominada FLD0 (Forming Limit Diagram zero) 9,12,13.
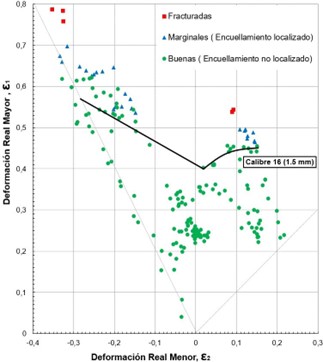
Figura 7 Curva límite de formabilidad de la lámina de acero inoxidable AISI 304 calibre 16 (1.5 mm). Fuente: Elaboración propia
De las figuras 7, 8 Y 9 se pudo determinar que los valores de FLD0 son los siguientes:
Para el calibre 16 está en torno a 0,02 para 𝜀2 y 0,4 para 𝜀1.
Para el calibre 18 está en torno a 0,01 para 𝜀2 y 0,38 para 𝜀1.
Para el calibre 20 está en torno a 0,01 para 𝜀2 y 0,45 para 𝜀1.
Las 3 curvas generadas para las láminas de este estudio tienen mejor comportamiento que los reportados por otros autores. Por ejemplo, Talyan et al. 23, para una chapa de acero AISI 304L de 1.168mm de espesor, con un FLD0 determinó valores en torno a 0,016 para 𝜀2 y 0,36 para 𝜀1. Rufini et al. 24, determinó un FLD0 en torno a 0 para 𝜀2 y 0,285 para 𝜀1 en una chapa de acero AISI 304 de 1.5 mm de espesor.
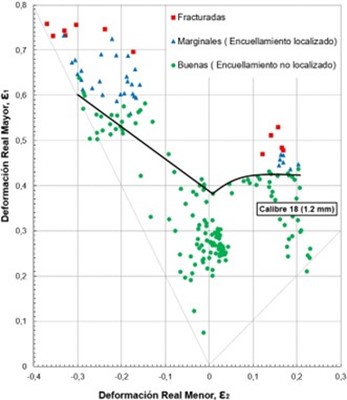
Fuente: Elaboración propia
Figura 8 Curva límite de formabilidad de la lámina de acero inoxidable AISI 304 calibre 18 (1.2 mm).

Fuente: Elaboración propia
Figura 9 Curva límite de formabilidad de la lámina de acero inoxidable AISI 304 calibre 20 (0.9 mm).
A modo ilustrativo en la Figura 10 se puede observar un diagrama comparativo entre las CLF para las 3 láminas objeto de estudio, junto a las predicciones determinadas por medio de ecuaciones de aproximación desarrolladas por Paul. 25.
En el caso de las curvas experimentales se observa que la lámina de calibre 20 tuvo mejor comportamiento que las de calibres 18 y 16, incluyendo los valores del FLD0, cuya curva está más arriba en el diagrama, Figura 10. Lo anterior coincide con los resultados de alargamiento total ε t y del exponente de endurecimiento por deformación n, reportados en la tabla 1, pero no corresponde con lo reportado por diferentes autores en el sentido de que las láminas de mayor espesor tienen mayor área segura en el diagrama límite de formabilidad FLD 9,12,21,25. Este comportamiento puede deberse a que, al tener un espesor tan pequeño, la respuesta al proceso de recocido de recristalización puede ser mejor, lo que se corresponde con un menor comportamiento anisotrópico, Δr más cercano a cero, y por tanto, presenta mejores propiedades intrínsecas 10, es decir, alargamiento hasta fractura y exponente de endurecimiento por deformación, lo que conlleva a un FLDo más alto.

Fuente: Elaboración propia
Figura 10 Comparativo de las 3 curvas límite de formabilidad desarrolladas experimentalmente junto a las predicciones utilizando la aproximación de Paul. 25, para el acero inoxidable AISI 304.
En cuanto a las predicciones, los valores de los FLD0 en términos de deformación real fueron calculados de acuerdo a Paul. 25, tomando como referencia de la tabla 1, los datos de resistencia última ( σ u ), anisotropía normal ( r ), elongación total ( ε t ), exponente de endurecimiento por deformación ( n ) y el espesor ( t ).
Los resultados de FLD0 fueron para 𝜀1 0,327; 0,336 y 0,352 en los calibres 20 (0.9 mm), 18 (1.2 mm) y 16 (1.5 mm) respectivamente, mientras que 𝜀2 es 0 en todos los casos 25. Aquí el comportamiento de las curvas en el lado derecho e izquierdo dependen únicamente de FLD0 para cada espesor.
Conclusiones
La mayor área cubierta por la CLF, el mayor FLD0 y su coincidencia con el mejor desempeño en propiedades como alargamiento total ε t , exponente de endurecimiento por deformación n y anisotropía planar Δ r , permiten inferir que las láminas de calibre 20 tienen mejor formabilidad que las de calibre 16 y 18. Este comportamiento, contrario a lo que se expone en estudios anteriores, puede deberse a que la lámina de este calibre, al ser muy delgada, presentó una mejor respuesta al proceso de recocido de recristalización durante su manufactura, y por tanto un menor comportamiento anisotrópico y mejores propiedades intrínsecas.
La caracterización experimental es indispensable para conocer el comportamiento exacto del material, puesto que las predicciones solo dan una idea general del desempeño y aunque estas se calculan en función de varias propiedades del material, dependen en mayor porcentaje del espesor de la lámina y del exponente de endurecimiento por deformación.
















