Numerical investigation of combustion in a panela furnace using openfoam

García-Sánchez, Gabriel F.; Chacón-Velasco, Jorge L.; Fuentes-Díaz, David A.; García-Sánchez, Gabriel F.; Chacón-Velasco, Jorge L.; Fuentes-Díaz, David A.

doi:10.25100/iyc.v26i1.13410

Services on Demand

Journal

Article

Indicators

Cited by SciELO
Access statistics

Ingeniería y competitividad

Print version ISSN 0123-3033On-line version ISSN 2027-8284

Ing. compet. vol.26 no.1 Cali Jan./Apr. 2024 Epub Feb 26, 2024

https://doi.org/10.25100/iyc.v26i1.13410

Article investigation

Numerical investigation of combustion in a panela furnace using openfoam

Investigación numérica de la combustión en un horno panelero utilizando openfoam

Gabriel F. García-Sánchez¹
http://orcid.org/0000-0001-8207-4713

Jorge L. Chacón-Velasco¹
http://orcid.org/0000-0001-9658-698X

David A. Fuentes-Díaz¹
http://orcid.org/0000-0002-6549-0712

^¹ Research Group on Energy and Environment (GIEMA). School of Mechanical Engineering. Universidad Industrial de Santander. Bucaramanga, Colombia. jchacon@uis.edu.co

Abstract

To develop biomass combustion as a viable renewable energy source it is necessary to improve the furnace efficiency and investigate the potential of agricultural wastes as fuels. Computational Fluid Dynamics (CFD) modeling is a valuable tool to accomplish these objectives, OpenFOAM is a powerful open-source CFD software that has been little used in this type of application. This paper reports the study of combustion in a device of great importance for Colombia, the panela furnace, using a model developed in OpenFOAM. The combustion chamber of a Ward-Cimpa furnace, measuring 2.68 m in width and 3.32 m in height was modeled. This model was validated, by comparing the simulated values of CO and temperature at the furnace exit with data taken from literature, resulting in differences of 13.72 % and 12.23 % respectively. These discrepancies are slightly lower than those reported in other studies about the subject. The model was employed to analyze the effect of the air-flow rate on the combustion performance. The findings indicate that the increase in air-flow causes an increase in combustion activity manifested in higher temperature and CO₂ emissions, which could indicate that in common operational conditions, the furnace operates under deficient air conditions and its performance could be improve by using higher air flow rates.

Keywords: combustion; Modeling; Biomass; Computational Fluid Dynamics; OpenFOAM

Resumen

Para desarrollar la combustión de biomasa como fuente viable de energía renovable es necesario mejorar la eficiencia de los hornos e investigar el potencial de los desechos agrícolas como combustibles. El modelado de dinámica de fluidos computacional (CFD) es una herramienta valiosa para lograr estos objetivos; OpenFOAM es un potente software CFD de código abierto que ha sido poco utilizado en este tipo de aplicaciones. Este artículo reporta el estudio de la combustión en un dispositivo de gran importancia para Colombia, el horno de panela, utilizando un modelo desarrollado en OpenFOAM. Se modeló la cámara de combustión de un horno Ward-Cimpa, que mide 2,68 m de ancho y 3,32 m de alto. Este modelo fue validado comparando los valores simulados de CO y temperatura a la salida del horno con datos tomados de la literatura, arrojando diferencias de 13,72 % y 12,23 % respectivamente. Estas discrepancias son ligeramente menores que las reportadas en otros estudios sobre el tema. El modelo se empleó para analizar el efecto del caudal de aire sobre el rendimiento de la combustión. Los hallazgos indican que el aumento en el flujo de aire provoca un aumento en la actividad de combustión que se manifiesta en una mayor temperatura y emisiones de CO2, lo que podría indicar que en condiciones operativas comunes, el horno opera en condiciones de aire deficientes y su rendimiento podría mejorarse utilizando mayor cantidad de aire. caudales.

Palabras clave: Combustión; Modelado; Biomasa; Dinámica de Fluidos Computacional; OpenFOAM

Introduction

Biomass is one of the most promising options to substitute fossil fuels and reduce greenhouse gas emissions. It has the advantages of CO₂ neutrality, worldwide availability and the possibility of production on demand of power and heat ¹. Combustion is the most popular technology for biomass conversion to energy ²; however, the emission of harmful gases from biomass combustion furnaces is still a significant problem that requires further research ¹. Computational Fluid Dynamics (CFD) modeling is a cost-effective tool to study and optimize the process; which is not a trivial task since successful modeling of solid combustion furnaces requires appropriate sub-models to simulate the relevant combustion, flow and transfer processes, and their interactions, whose complexity affects the accuracy of the results and computational time ³. Due to that, it is a topic that is still under investigation; a full review is given in the papers of Karim and Naser ⁴, Dernbecher et al. ⁵, Bhuiyan et al. ⁶, Khodaei et al. ⁷ and García et al. ⁸^,⁹. Moving grate furnaces have been the most studied systems because they are widely used in industry ⁸; however, fixed bed systems of low power have gained popularity in recent years due to their low operating cost, simplicity and low requirements in terms of fuel preparation and transportation ⁷^,¹⁰^,¹¹. Traditional panela furnace is a kind of fixed-bed device of great relevance for Colombia, which is the second producer of panela (jaggery) in the world after India . Most of the panela production activities continue to be carried out in small-scale units with low efficiency and low quality standards ¹²^-¹⁹, which has meant that in many cases the product is not suitable for export and is destined almost entirely for domestic consumption ¹⁶^,²⁰. Few studies have been published on CFD modeling of traditional panela furnaces, some examples are the works of Mendieta and Sanchez ²¹, Guevara ²² and Quispe ²³, who simulated the sugarcane bagasse combustion in Ward-Cimpa chambers by 1D, 2D and 3D models.

OpenFOAM (Open Field Operation and Manipulation) is a powerful engineering tool developed at Zagreb University that is often used in industrial applications ²⁴. It has significant advantages such as being a free open-source constantly under development with a continuous growing community and including solvers for several applications ²⁵. However, there are relatively few OpenFOAM-based models reported in the literature to study the combustion of solid biomass. Most of the studies of this subject are performed using the software ANSYS®⁸^,⁹. In order to contribute to the study of the combustion in panela furnaces, in the current work, a comprehensive two-dimensional numerical model was developed in OpenFOAM. An eulerian-lagrangian approach was used to simulate the gas and solid particles behavior in a Ward-Cimpa chamber fueled with sugarcane bagasse. The model includes the sub-models: Partially Stirred Reactor (PaSR), k-epsilon and P1 for gas combustion, turbulence and radiation, respectively. The calculated values of CO and temperature at the chamber's exit were compared data taken from literature, showing good agreement between them. The model was used to test the influence of the air-flow rate in the temperature and the emissions of CO, CO₂ and CH₄ at the exit of the chamber.

Methodology

Computational domain

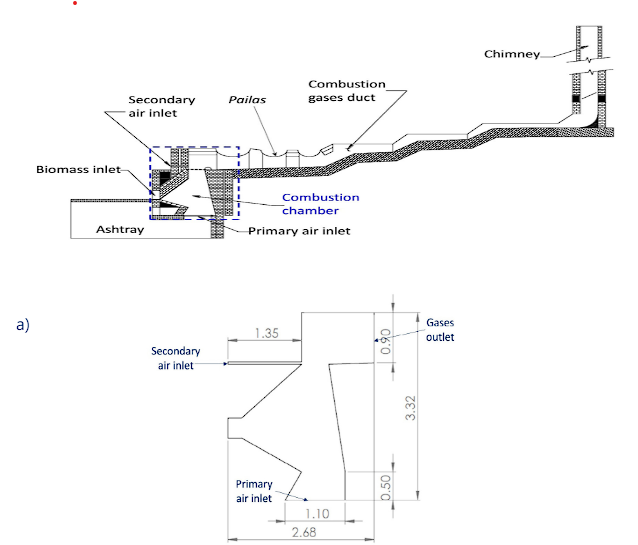
The computational domain is a 2D representation of the combustion chamber within a Ward-Cimpa furnace, as illustrated in Figure 1. In Figure 1a, the entire system ²², is depicted, wherein sugarcane bagasse undergoes combustion within the chamber. The resultant combustion gases flow towards the pailas, where the sugarcane juice is boiled to produce panela. Subsequently, the gases exit through the chimney. The specifically modeled portion of the system (the combustion chamber) is detailed in Figure 1b. The dimensions of this chamber were adopted from Guevara's research ²². The domain was discretized using a structural mesh generated through the tool blockMesh. A mesh convergence analysis was conducted by testing various mesh refinements to find a mesh whose results are independent of the size.

Figure 1 Ward-Cimpa furnace. a) Whole system (adapted from Guevara (22)) y b) computational domain, dimensions in meters.

Fuel and operating conditions

The main properties of the fuel (sugarcane bagasse) were taken from the literature ²²^,²⁶, they are presented in Table 1. Those values were obtained from experimental tests such as the elemental and proximate analyses.

Table 1 Fuel properties

Property Type	Property	Value
Physical	Particle density	317.5 kg/m³
	Apparent density	127 kg/m³
	Diameter	4.01 mm
Chemical	Chemical formula	CH_2.0526O_0.6658
	Moisture	50%
	Volatile fraction	41.25%
	Fixed carbon	8.05%
	Ashes	0.70%
	pyrolysis kinetics parameters	A = 5x10²² s^-1
Ea = 2.67x10⁸
J/kmol
f(α)) = (1-α)
Thermal	Specific heat	2460 J/kg.K
	Emissivity	1
	Pyrolysis Temperature	500 K

The furnace walls are made of firebrick, therefore, adiabatic conditions were assumed at the boundary walls. It is a batch reactor, the biomass fuel fills part of the furnace from the bottom to 1.1 m above, forming the fuel bed. The solid fuel reacts with the primary air from the bottom and the gases released mixture with the secondary air to complete combustion. Three mass flow rates were studied, which are presented in cases A, B and C of Table 2. Case B was used to validate the model by comparing predicted results with design data at these conditions. In cases A and C, the air flow is 30% less and 30% more that in the case B, respectively, with which the effect of the air in the process was analyzed.

Table 2 Primary and secondary air flow rates

Case	Primary air flow rate [kg/s]	Secondary air flow rate [kg/s]
A	0.2067	0.1034
B	0.2953	0.1477
C	0.3839	0.1920

Model description

The model uses an Eulerian-Lagrangian approach for modeling the gas (freeboard) and solid (fuel bed) phases. The governing equations are solved in the gas phase, for which its source terms are determined from the submodels of combustion (c), radiation and particles (p). The latter is decomposed according to the phenomenon that is represented, i.e., the stage of the process (evaporation - ev or pyrolysis - dv), the particle drag force (dr) and thermal convection (cv). Equations 1 to 8 presents the mentioned governing equations and the decomposition of its respective source terms.

Mass:

∂ρg∂t+∇·ρgUg=Sm (1)

Sm=Sp,m=Sp,mdv+Sp,mev (2)

Energy:

∂ρgh∂t+∂ρgK∂t+∇·ρgUgh+∇·ρgUgK-∇·αeff∇h=-∇p+ρgUg·g+Sh (3)

Sh=Sp,h+Sc,h+Sr,h=Sp,hdv+Sp,hev+Sp,hcv+Sc,h+Sr,h (4)

Momentum:

∂ρgUg∂t+∇·ρgUgUg-∇·τg-∇·ρgRg=-∇p+ρgg+Su (5)

SU=Sp,u=Sp,udv+Sp,uev+Sp,udr (6)

Chemical Species:

∂ρgYi∂t+∇·ρgUgYg-∇·Deff∇ρgYi=Sy (7)

Sy=Sp,y+Sc,y=Sp,ydv+Sp,yev+Sc,y (8)

The solver coalChemistryFoam of OpenFOAM was used to solve this system. Table 3 shows the submodels considered to determine the terms of equations 2, 4, 6 and 8. There

Table 3 Submodels used

Terms	Submodel	Expressions of the submodels	References
𝑆^𝑑𝑣 _𝑝,𝑚, 𝑆^𝑑𝑣 _𝑝,ℎ , 𝑆^𝑑𝑣 _𝑝,𝑢 and 𝑆^𝑑𝑣 _𝑝,𝑦	One-component single reaction mechanism	dadt=fαA exp-EaRuT ( 9)	²⁷
𝑆^𝑒𝑣 _𝑝,𝑚, 𝑆^𝑒𝑣 _𝑝,ℎ, 𝑆^𝑒𝑣 _𝑝,𝑢, and 𝑆^𝑒𝑣 _𝑝,𝑦	Equilibrium approach	(10) (11) (12)	²⁸
𝑆^𝑐𝑣 _𝑝,ℎ	Ranz Marshall	Nup=2.0Res12Prs13 (13)	²⁹^,³⁰
𝑆_𝑐,ℎ and 𝑆_𝑐,𝑦	Partially Stirred Reactor model	fmc=c1c0τ=kfmc1 (14) k=τcτc+τmix ( 15) τmix=Cmixkε ( 16)	³¹
𝑆_𝑟,ℎ	P-1	∇·13a+σef∇G-aG=-4agsσT4-4Ep ( 17)	³²
𝑆^𝑑𝑟 _𝑝,𝑢	Drag Force	Fdrag=Udiff0.75mpμcCdρDp2 ( 18) 0.424Res;Res>1000; 241+6Res-23;Res≤1000 (19)	³²

Results

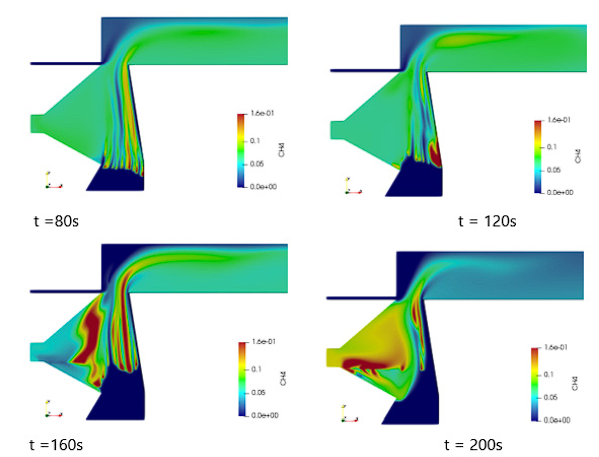
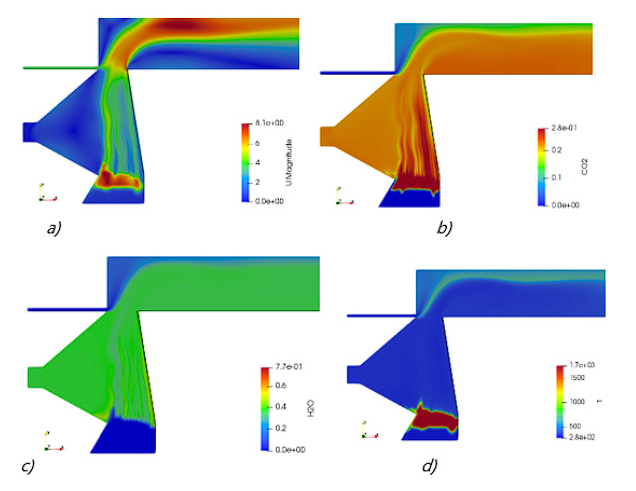
Firstly, case B was simulated; Figures 2 and 3 present results for that operating condition. Figure 2 shows the CH₄ profile at four instants of the simulation and figure 3 presents the velocity, CO₂, H₂O and temperature profiles in the furnace at 100 seconds. Biomass contains a large amount of volatile matter, which is released at the pyrolysis stage, it usually comprises CO, CO₂, H₂, CH₄ and tar ⁷. The zone of volatiles production (such as CH₄ and CO₂) is the zone where the pyrolysis stage is taking place and its movement indicates the progress of the ignition front, which can be seen in figure 2. The three combustion stages (drying, pyrolysis and char combustion) occur from the bottom to the top of the bed. At the bottom, the char combustion occurs by the primary air and above it pyrolysis and drying occur due to the heat received by conduction and radiation from below. The maximum solid temperature is encountered at the lower part of the bed where the moisture has been driven out and more oxygen is available for the char oxidation reaction. The maximum gas temperature is presented near the secondary air inlet, where secondary air reaches the volatiles and completes the combustion. These maximum temperature values are similar to the ones reported in the literature ²²^,²³.

Figure 2 Mass fraction of CH₄ at four different instants.

Figure 3 Results at 100 seconds: a) Velocity, b) CO₂, c) H₂O and d) Temperature fields

Table 4 shows the comparison between the average values of temperature and CO at the furnace outlet obtained in this study and presented in the work of Guevara ²². The outlet temperature and CO mass fraction, taken from the work of Guevara, are design values used to represent the real performance of those devices during its development. The relative error (RE) presented in the table is slightly lower than that reported in other studies about combustion modeling of similar panela furnaces ²¹^,²², which indicates that the model is suitable for the analysis of the device. Many factors affect the solid combustion process; therefore, it is not easy to explain the difference between values in the table; the most significant factor may be the simple combustion model used for the fuel bed. The three stages of the process transfer mass from the particle to the gas phase and are dependent on the particle geometry and complex coal chemistry reactions that break down the solid structure to release gases ³². The present model does not take into account this level of detail; instead, spherical particles are assumed and the user specifies the fraction of mass lost by the particles at the beginning of the simulation. The assumption that fuel particles are spherical introduces a variation in the heat transfer area, affecting radiation and convection within the chamber. Additionally, the fractions of volatile gases included prior to simulation are derived from biomass proximate analysis, conducted under conditions that may differ from those within the combustion chamber. Besides, the thermally thin assumption for fuel particles neglect temperature gradients inside the particle, which affect the surface temperature, that means a less drastic variation of the bed temperature ³³^,³⁴. However, the mentioned simplifications are justified by the reduction in the computational cost of the simulation. More accurate results could be obtained by employing a more detailed reaction mechanism for the three combustion stages and using a finer mesh that enables the consideration of internal gradients and the original shape of the particles. Nevertheless, incorporating these changes would significantly increase the complexity of the model and necessitate higher computational time.

Table 4 Comparison of literature and simulated data

Parameter	Present Work	Literature	Difference	RE [%]
Temperature [K]	1352.33	1205	147.33	12.23
CO [%]	2.99	2.63	0.36	13.72

The temperature and emissions are two key performance indices of fixed bed combustion, the former is an index of the thermal conversion efficiency and the latter is an index of the pollution caused by the device. The combustion air is the main control parameter of biomass furnaces, if the air is less than the stoichiometric amount required, the combustion will be incomplete and only part of the fuel energy will be converted into thermal energy, and if there is too much excess air, there will be a chilling effect on the furnace that decreases combustion efficiency ²⁷. Under low air-flow conditions, there is not enough oxygen to complete the homogeneous reactions and there is a large amount of unburned species. If the air-flow rate increases, fuel conversion increases linearly, followed by a stage of slow increase until it reaches a peak and starts decreasing significantly due to the intensification of the convective cooling effect ⁷. This trend is reflected in the emissions a temperature values.

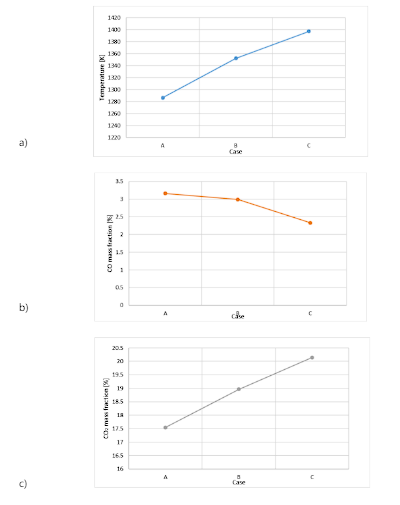
Using the presented model, we calculated the temperature and the average CO and CO₂ emissions at the furnace outlet for the air-flow rates described in table 2 (Cases A, B and C). Those results are presented in Figure 4. As can be seen, an increase in air-flow rate demonstrates an almost linear elevation in temperature and CO₂ emissions, accompanied by a decrease in CO emissions. This is due to the oxygen content, CO is an intermediate product of combustion, more oxygen leads to a more complete process and therefore CO reacts to form CO₂. It indicates that in common operational conditions the combustion is limited by oxygen, i.e, the furnace operates under deficient air conditions. According to the literature ⁷^,³⁵, if the airflow was to increase further, the cooling effect would become more significant, potentially causing a plateau and subsequent decline in CO₂ emissions due to a less complete reaction. We suggest using higher air flow rates to improve combustion, further studies are required to identify the optimum operational point of the furnace.

Figure 4 Temperature and average emissions at the furnace outlet for cases A, B and C. a) Temperature, b) CO and c) CO₂

Conclusions

A comprehensive two-dimensional CFD modeling of solid biomass combustion and associated emission in a Ward-Cimpa panela furnace has been performed. The model was implemented in the open-source software OpenFOAM, using an eulerian-lagrangian approach for the freeboard and the fuel bed. It was tested by comparing the predicted temperature and CO values at the furnace outlet with those obtained from the literature. The relative error percentages for the mentioned values were 12.23 % and 13.72 %, respectively; which are values slightly lower than those reported in other studies about the subject. These predictions could be improved by considering a more detailed model for the fuel bed, especially for the char combustion stage; however, it would increase the complexity and the computational cost.

The model was used to analyze the influence of the air-flow rate in the furnace performance. It was found that there is an increase in the combustion activity with the increase in air-flow rate, which can be seen by the increase in temperature and CO₂ emissions, and the decrease of CO emissions. These results indicate that higher air-flow rates could improve the furnace's performance. Further studies are required to identify the optimal operating point of the analyzed furnace.

Nomenclature

h enthalpy

Kkinetic energy

S source term

Ɛrate of dissipation of turbulent kinetic energy

σ Stefan-Boltzmann constant

α conversion degree

aoverall absorption coefficient

Girradiation

τ residence time in the reactive structure

cspecies concentration

Apre-exponential factor

D _eff effective mass diffusivity

α _eff effective thermal diffusivity

R_gReynolds stress term

U _p particle velocity

m _p particle mass

T _p particle temperature

A _p particle superficial area

h _c convective heat transfer coefficient

h _m convective mass transfer coefficient

T _∞ ambient temperatura

C _m moisture concentration

E _a activation energy

R _u universal gases constant

E _p emission contribution of particles

Nu Nusselt number

Re Reynolds number

Pr Prandlt number

fmreaction rate

Acknowledgment

Funding from Minciencias, Ministry of National Education, Ministry of Industry, Commerce and Tourism and ICETEX, Scientific Ecosystem - Colombia Científica, Fund Francisco José de Caldas, through Contract RC-FP44842-212-2018, is gratefully acknowledged.

Disclosure statement: The authors report there are no competing interests to declare. Data availability statement: The authors confirm that the data supporting the findings of this study are available within the article.

References

1. Mousavi SM, Fatehi H, Bai XS. Numerical study of the combustion and application of SNCR for NOx reduction in a lab-scale biomass boiler. Fuel. 2021;293:120154. [ Links ]

2. Buchmayr M, Gruber J, Hargassner M, Hochenauer C. Performance analysis of a steady flamelet model for the use in small-scale biomass combustion under extreme air-staged conditions. Journal of the Energy Institute. 2018;91(4):534-48. [ Links ]

3. Chaney J, Hao L, Jinxing L. An overview of CFD modelling of small-scale fixed-bed biomass pellet boilers with preliminary results from a simplified approach - ScienceDirect. Energy Conversion and Management. 2012;63:149-56. [ Links ]

4. Karim MdR, Naser J. Progress in Numerical Modelling of Packed Bed Biomass Combustion. In 2014. [ Links ]

5. Dernbecher A, Dieguez-Alonso A, Ortwein A, Tabet F. Review on modelling approaches based on computational fluid dynamics for biomass combustion systems. Biomass Conv Bioref. 2019;9(1):129-82. [ Links ]

6. Bhuiyan AA, Karim MdR, Naser J. Chapter 11 - Modeling of Solid and Bio-Fuel Combustion Technologies. In: Khan MMK, Hassan NMS, editors. Thermofluid Modeling for Energy Efficiency Applications. Academic Press; 2016. p. 259-309. [ Links ]

7. Khodaei H, Al-Abdeli YM, Guzzomi F, Yeoh GH. An overview of processes and considerations in the modelling of fixed-bed biomass combustion. Energy. 2015;88:946-72. [ Links ]

8. García Sánchez G, Chacón Velasco J, Fuentes Díaz D, Jaramillo Ibarra J, Martínez Morales J. CFD modelling of biomass boilers - a review of the state of the art. Respuestas. 2020;25(3):262-273. [ Links ]

9. García Sánchez GF, Chacón Velasco JL, Rueda-Ordoñez YJ, Fuentes Díaz DA, Martínez Morales JR. Solid biomass combustion modeling: Bibliometric analysis and literature review of the latest developments in OpenFOAM based simulations. Bioresource Technology Reports. 2021;15:100781. [ Links ]

10. Buchmayr M, Gruber J, Hargassner M, Hochenauer C. A computationally inexpensive CFD approach for small-scale biomass burners equipped with enhanced air staging. Energy Conversion and Management. 2016;115:32-42. [ Links ]

11. Yin C, Rosendahl LA, Kær SK. Grate-firing of biomass for heat and power production. Progress in Energy and Combustion Science. 2008;34(6):725-54. [ Links ]

12. Ordoñez RA, Hernández CA, Pedraza LF. Modelado de un Sistema de Evaporación de Múltiple Efecto para la Producción de Panela (Azúcar no Centrifugado). Información tecnológica. 2012;23(6):105-20. [ Links ]

13. Arredondo HIV, Janna FC, Santamaría AFA. Diagnóstico energético de los procesos productivos de la panela en Colombia. Revista Facultad Nacional de Agronomía. 2004;57(2):2453-65. [ Links ]

14. Velásquez H, Janna F, Agudelo A. Diagnóstico exergético de los procesos productivos de la panela en Colombia. Revista Energética. 2006;35:15-22. [ Links ]

15. Santamaíia A, Augusto C, Pinzón Pérez J. Diseño de la Implementación de una Adaptación Tecnológica Basada en Energía Solar para la Producción Sostenible de Panela en un Trapiche del Municipio de San Benito Santander; 2016. [ Links ]

16. Montoya C, Giraldo P. Propuesta de diseño de planta de procesamiento de caña para la elaboración de panela. [Medellín-Colombia]: Universidad Nacional de Colombia; 2009. [ Links ]

17. Vargas P, Aurelio M. Procesos de fabricación de panela y su aplicación a proyectos de automatización para el caso colombiano; 2015. [ Links ]

18. Corporación colombiana de investigación agropecuaria, AGROSAVIA. La tecnología del cultivo de la caña panelera. 1999 [cited 2017 Jul 11]; Available from: http://agris.fao.org/agris-search/search.do;jsessionid=C51A611D4E1E0DAC6FD58F2957D643BC?request_locale=fr&recordID=CO2001000510&query=&sourceQuery=&sortField=&sortOrder=&agrovocString=&advQuery=&centerString=&enableField= [ Links ]

19. Prada L, García H, Chaves A. Efecto de las variables de evaporación: presión y flujo calórico en la calidad de la panela. Agroindustria. 2014;16(1):7-23. [ Links ]

20. Osorio G. Manual Técnico. Buenas prácticas agrícolas (BPA) y buenas prácticas de manufactura (BPM) en la producción de caña y panela. 2007. 200 p. [ Links ]

21. Mendieta O, Sanchez Z. Ajuste de un modelo matemático para la combustión de bagazo de caña en una cámara Ward-Cimpa. Ciencia y Tecnología Agropecuaria. 2014;15(2):133-51. [ Links ]

22. Guevara Enciso JI. Modelo computacional de la combustión del bagazo de caña en una cámara de combustión tipo ward-cimpa de una hornilla panelera. [Maestría]. Universidad de los Andes; 2014. [ Links ]

23. Quispe Chanampa CN. Metodología de Simulación Numérica de la Combustión de Bagazo Aplicada en la Cámara de una Hornilla Panelera. Mecánica Computacional. 2014;33(4):245-61. [ Links ]

24. Rückert FU, Lehser-Pfeffermann D, Theis D, Kim JP, Schargen A, Zorbach I, et al. A new Simulation Model for Grate Firing Systems in OpenFOAM. Energy. 2021;216:119226. [ Links ]

25. Kasper R. Particle Simulation with OpenFOAM(r). In Haus der Wissenschaften, Braunschweig, Germany; 2017. [ Links ]

26. Mothé C, Miranda I de. Characterization of sugarcane and coconut fibers by thermal analysis and FTIR. Journal of Thermal Analysis and Calorimetry. 2009;97(2):661-5. [ Links ]

27. García Fernández R. Modelización cinética y optimización de parámetros de combustión en calderas de biomasa. [Doctorado]. [España]: Universidad de Oviedo; 2014. [ Links ]

28. GOH YR, YANG YB, ZAKARIA R, SIDDALL RG, NASSERZADEH V, SWITHENBANK J. Development of an Incinerator Bed Model for Municipal Solid Waste Incineration. Combustion Science and Technology. 2001;162(1):37-58. [ Links ]

29. Ranz WE, Marshall WR. Evaporation from drops: Part I. Chemical Engineering Progress. 1952;48(3):141-6. [ Links ]

30. Ranz WE, Marshall WR. Evaporation from drops: Part II. Chemical Engineering Progress. 1952;48(4):173-80. [ Links ]

31. Nordin PAN. Complex Chemistry Modeling of Diesel Spray Combustion; 2001. [ Links ]

32. Dunn C. Computational modeling of coal devolatilization and soot formation in OpenFoam [Master]. [EEUU]: University of Wyoming; 2018. [ Links ]

33. Gómez MA, Porteiro J, Patiño D, Míguez JL. CFD modelling of thermal conversion and packed bed compaction in biomass combustion. Fuel. 2014;117:716-32. [ Links ]

34. Karim MdR, Naser J. Numerical study of the ignition front propagation of different pelletised biomass in a packed bed furnace. Applied Thermal Engineering. 2018;128:772-84. [ Links ]

35. Patiño Vilas D. Análisis experimental de combustión de biomasa en un quemador de lecho fijo. Universidade de Vigo; 2009. [ Links ]

Notes:

How to cite? García-Sánchez, G.F., Chacón-Velasco, J.L., Fuentes-Díaz, D.A. Numerical investigation of combustion in a panela furnace using openfoam. Ingeniería y Competitividad, 2024, 26(1): e-20313410. https://doi.org/10.25100/iyc.v26i1.13410

Received: December 04, 2023; Accepted: February 16, 2024

This is an open-access article distributed under the terms of the Creative Commons Attribution License