Introduction
Direct current (DC-DC) converters are used in applications that require voltage step-up or step-down, contingent upon the topology of each converter. The SEPIC converter, for instance, facilitates both voltage boosting and bucking, rendering it suitable for renewable energy applications, where it maintains regulation over output DC voltage levels 1. One such converter application is the implementation of Maximum Power Point Tracking (MPPT) in photovoltaic or wind generation systems, accomplished through control strategies 2. Understanding the mathematical models that represent converter dynamics is crucial for designing controllers capable of meeting the specific requirements of the intended applications. A converter may be represented by transfer functions, as in 3,4), where the ratios between duty cycle and output voltage, as well as between the input voltage to output voltage are presented. These transfer functions enable the identification of the converter's response to disturbances in each of its parameters or characteristics. Another representation is the switched model, which comprehensively describes the behavior of a converter and is derived from the operating modes 5-14. This model is useful for obtaining the converter’s small-signal model 4,6,11,13,15,16, which is essential for designing linear controllers 17. In the reviewed literature, most authors obtain models using ideal elements, while in 5,18-20 the authors propose transfer functions and switched models with non-ideal elements, providing models that are more approximate to the implemented circuit. However, they do not provide control actions for the converter.
In converter control, output voltage regulation is commonly implemented 3,7,11-13,15,16,21,22, to ensure that the converter maintains an approximately constant output voltage despite fluctuations in the input voltage supplying the converter or variations in connected load.
As a contribution to the literature review, this article introduces the small-signal mathematical model of the SEPIC converter, incorporating the internal resistances of the inductors. Using this non-ideal model, an analog PI controller is proposed to regulate the output DC voltage.
The rest of the paper is structured as follows. In Section 2, the converter operation modes are presented. Following this, Section 3 demonstrates the converter switched model. Section 4 details the small-signal model. The controller designed for the converter is discussed in Section 5. The simulation results of the controlled converter model, accounting for variations in both input voltages and loads are given in Section 6. Finally, conclusions drawn from the analysis of results and compliance with the specifications defined for the performance of the SEPIC converter are presented.
Operation modes
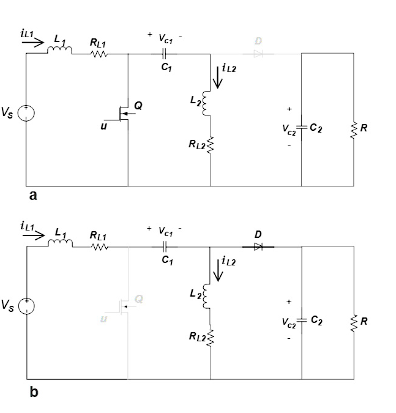
The SEPIC converter can raise or lower the output voltage levels. This feature enables the regulation of changes in DC levels in photovoltaic farms 1. Figure 1 shows the SEPIC converter, which consists of four elements that store energy: two inductors with internal resistances, two capacitors, a MOSFET, a Diode and a resistor.
This converter has two configurations based on the switching states of the MOSFET. When the MOSFET is in the activation state, configuration I is presented, whereas, upon deactivation, configuration II is established, as depicted in Figure 2.
In configuration I, the MOSFET is switched on and current flows through it, the source 𝑉𝑠, the inductor 𝐿1 and the resistor 𝑅𝐿1, As a result, the source charges the inductor 𝐿1. An effect of this activation is that the circuit diode turns off; consequently, condenser 𝐶2 supplies energy to the output resistance. When the control signal deactivates the MOSFET, configuration II appears as observed in Figure 2b. The diode is activated because the voltage at the anode terminal is higher resulting from the addition of the voltages of the source and the charged inductor. By applying Kirchhoff's voltage and current laws in the configurations, the switched model is constructed, as presented in the following section.
Switched model
The switched model of the SEPIC converter is constructed using the state variables, which include the currents 𝑖𝐿1, 𝑖𝐿2 in the inductors 𝐿1 and 𝐿2, respectively, along with the voltages 𝑣𝑐1 and 𝑣𝑐2 accross the condensers 𝐶1 and 𝐶2, respectively.
In Configuration I, the voltages and currents required to obtain the state equations are determined from Eq. (1). For configuration II, the state equations are presented in Eq. (2)
The switched model in state space for the SEPIC converter is constructed by grouping Eq. (1) and Eq. (2). The result is presented in Eq. (3). The control signal 𝑑(𝑡) is 1 when the MOSFET must be activated and 0 otherwise.
To derive the average model, the moving average of Eq. (3) must be calculated, replacing the switching signal 𝑑 with its average, defined as 𝛼. The average model of the SEPIC converter in state space is presented in Eq. (4).
Small-signal model
The small-signal model is defined based on the average model, the converter equilibrium points, and the variations around the operating point in each of the state variables. The following are the steps and equations that enable the calculation of each of these aspects, culminating in the presentation of the small-signal model.
The equilibrium points are calculated by setting Eq. (4) to zero, and solving for each value of 𝑖??1, 𝑖𝐿2, 𝑣𝑐1 and 𝑣𝑐2. The subscript 𝑒 is added to indicate each value of current and voltage at the equilibrium point. These are presented in Eq. (5), enabling the determination of the steady-state response to each state variable of the SEPIC converter.
The tilde ~ indicates the variations around the operation point. Eq. (6) defines the variations around the operational point for each state variable and the switching signal.
The small-signal model is acquired by substituting Eq. (6) into Eq. (4), omitting terms of order higher than one 17. This model is described in Eq. (7).
Controller design
The converter’s design parameters are proposed for a 2-kW load power. The values for inductors and condensers are obtained from Eq. (8). These values are determined to prevent exceeding a current ripple higher than 40% in the inductors, and 1% and 2% in condenser voltages 𝐶1 and 𝐶2, respectively.
The established parameters for the converter are summarized in Table 1. These parameters are used in the converter’s small-signal model described in Eq. (7). With this model, the transfer function 𝐺(𝑠) is obtained, as presented in Eq. (9). This function relates the output voltage 𝑣𝑐2(𝑠) with the switching signal 𝛼(𝑠).
Table 1 System parameters
| Parameter | Symbol | Value |
|---|---|---|
| Load power | 𝑃 | 2 kW |
| Input DC voltage | 𝑉𝑠 | 90 V |
| Switching frequency | 𝑓𝑠 | 50 kHz |
| Duty ratio | 𝛼𝑒 | 0.355 |
| Output DC voltage | 𝑣𝑐2 | 48 V |
| Output current | - | 41.67 A |
| Current ripple in 𝐿1 and 𝐿2 | 𝛥𝐼𝐿 | 10 A |
| Voltage ripple in 𝐶1 and 𝐶2 | 𝛥𝑣𝑐1, 𝛥𝑣𝑐2 | 0.95 V, 0.96 V |
| Inductors 𝐿1 and 𝐿2 | 𝐿1, 𝐿2 | 80 μH |
| Internal resistance in inductors 𝐿1 and 𝐿2 | 𝑅𝐿1, 𝑅𝐿2 | 50 mꭥ |
| Capacitor 𝐶1 | 𝐶1 | 330 μF |
| Capacitor 𝐶2 | 𝐶2 | 680 μF |
| Load (Resistor) | 𝑅 | 1.15 ꭥ |
The controller that improves the dynamic response of the converter is designed based on the root locus technique using MATLAB® RLTOOL. The controller design specifications include a settling time at output voltage 𝑣𝑐2 of 25ms with 0% override.
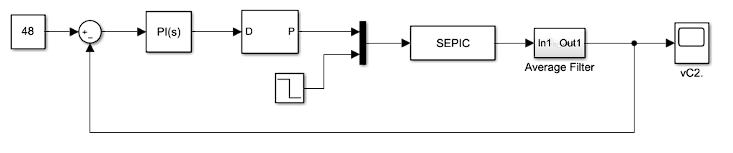
To satisfy the control objective, a PI controller with constants 𝐾𝑝= 0.00035 and 𝐾𝐼= 0.686 is used. By performing the feedback described in Figure 3, the closed-loop response of the SEPIC converter is obtained in the state space representation loaded in the block called SEPIC. The control signals and the input voltage signal 𝑉𝑠 enter this block. Variations in the voltage signal 𝑉𝑠 are enacted through the step signal with amplitudes of 85 and 90 V. The proposed control scheme allows the voltage to be regulated to 48 V.
Figure 4 illustrates the SEPIC converter circuit. Circuit simulation was performed in MATLAB SIMULINK using the TOOLBOX SIMSCAPE. To change the input circuit voltage, a source controlled by a step signal was used.
Due to the switching action of the control signal, a filter is incorporated at the output of the SEPIC converter that obtains the average value of the voltage signal. The simulation results are shown in the next section.
Results
This section presents the simulation results of the SEPIC converter with a 2-kW load using the MATLAB®/ SIMULINK® simulation tool, using the values of the converter parameters shown in Table 1. Figure 5 displays the open-loop output voltage of the mathematical model and the SEPIC converter circuit. At time 80 ms the input DC voltage changes to 85 V. According to Eq. (5), the output voltage of the converter in steady state 𝑉𝐶2𝑒 is directly proportional to the input voltage; therefore, the output voltage is reduced.
The output voltage of the SEPIC converter controlled for the model and the converter circuit using discrete elements is shown in Figure 6. The initial configuration of the converter is established with the parameters in Table 1. At the time instant 80 ms, the input voltage changes to 85 V. The simulation results demonstrate that the settling time for both the model and the circuit is less than 25 ms, indicating that the proposed controller satisfies the design specifications around the operating point.
Figure 7 shows the controller’s output signal. The magnitudes of the control signals for the proposed model and the simulated circuit with discrete elements are less than 0.5 V. Therefore, the controller could be implemented in either an analog or digital manner.
Figure 8 illustrates the controlled converter’s response to load changes. During the 0 to 100 ms interval, the charge corresponds to 1.15 ꭥ; however, from time point 80 ms onwards, it increases by 5%. The simulation results show that the proposed PI controller regulates the output voltage in the face of changes close to the established operating point, specifically in the DC input voltage and the load connected to the converter.
Conclusions
The mathematical model proposed in this article incorporates the internal resistances of the inductors, providing a closer approximation to the physical implementation of the converter. This enhancement enables more precise controller design to meet the desired specifications, as the operational point of the SEPIC converter involves more variables than the associated dynamics.
The model presented can be applied in the analysis of renewable energy systems, energy storage, and systems interconnected to the grid. Such applications require an analysis of the efficiency and performance of control systems in mitigating disturbances caused by the load or the DC power supply.
The simulation results indicate that the proposed controller can be implemented in both analog or digital systems. This is evident as the controller effort signal remains below 0.4 V for the configurations established around the operating point variations.