Artículo de investigación/Research article

Cálculo Computacional de las Propiedades Magnéticas de la Superred MnO/ZnO

Computational Calculation of the Magnetic Properties of MnO/ZnO Superlattice

Miguel J. Espitia-Rico ¹, John H. Díaz-Forero ²

¹Ph.D. en Ciencias Física, Facultad de Ingeniería, Universidad Distrital Francisco José de Caldas, Bogotá-Colombia, mespitiar@udistrital.edu.co

²Ms.C. en Ciencias Física, Facultad de Ingeniería, Universidad Distrital Francisco José de Caldas, Bogotá-Colombia, jhdiazf@udistrital.edu.co

Fecha de recepción: 3 de julio de 2015 / Fecha de aceptación: 11 de noviembre de 2015

Como citar / How to cite

M.J. Espitia-Rico y J.H. Díaz-Forero, “Cálculo computacional de las propiedades magnéticas de la superred MnO/ZnO”, Tecno Lógicas, vol. 19, no. 36, pp. 41-48, 2016.

Resumen

En este trabajo se realizaron cálculos por primeros principios basados en la Teoría del Funcional de la Densidad, con el fin de investigar las propiedades estructurales, electrónicas y magnéticas de la superred MnO/ZnO en la estructura wurtzita. Se utilizó el método Ondas Plana Aumentadas y Linealizadas Potencial Completo (FP LAPW), tal como está implementado en el código computacional Wien2k. Los efectos de intercambio y de correlación entre los electrones fueron tratados por medio de la Aproximación de Gradiente Generalizado (GGA) de Pedew, Burke y Ernzerhof (PBE). El análisis de las propiedades estructurales muestran que el valor del módulo de volumen es alto, por tanto, esta superred es bastante rígida y es buena candidata para aplicaciones en dispositivos que deban trabajar altas temperaturas, altas potencias y en recubrimientos duros. Los estudios de la densidad estados muestran que la superred posee un comportamiento semimetálicos con polarización de espín en el estado base del 100% y un momento magnético de 5 µβ/atomo-Mn, el estado ferromagnético proviene de la hibridación y polarización de los estados Mn-3d en mayor contribución y de los orbitales O-2p en menor contribución que atraviesan el nivel de Fermi. Debido a esta propiedad la superred puede ser potencialmente usada en espintrónica.

Palabras clave: DFT, superred, propiedades magnéticas, momento magnético, ferromagnetismo semimetálico

Abstract

First-principle calculations were performed in order to investigate the structural, electronic and magnetic properties of 1x1 MnO/ZnO superlattice in the wurtzite-type structure. The full-potential linearized augmented-plane-wave (FP-LAPW) method was used, as implemented in the WIEN2k computational code. Exchange and correlation effects are treated using the generalized gradient approximation (GGA) of Perdew-Burke-Ernzerhof  (PBE). The analyze of the structural properties show that the value of the bulk moduli is high, therefore is quite rigid and this feature makes them good candidates for possible application in devices that have to operate at high temperatures, under high power, and in hard coatings. The electronic density studies show that the MnO/ZnO superlattice have a half-metallic behavior with a magnetic spin polarization of 100% and a magnetic moment of 5 µβ/atom-Mn in the ground state. The ferromagnetic state comes from the hybridization of the Mn-3d and O-2p states that cross the Fermi level. This superlattice is a good candidate for spintronic applications.

Keywords: DFT, superlattice, magnetic properties, magnetic moment, half-metallic ferromagnetism.

1. Introducción

El ZnO es un semiconductor de gap de banda directo que cristaliza en la estructura hexagonal tipo wurtzita[1]; posee gran estabilidad química y térmica, excelentes propiedades electrónicas y optoelectrónicas, por lo que el rango de aplicaciones tecnológicas de este material incluye: electrodos conductores transparentes en celdas solares, diodos laser, fotocatálisis [2], dispositivos ópticos [3], en productos cosméticos como pantallas solares [4] y aplicaciones piezoeléctricas en dispositivos de ondas acústicas superficiales [5], [6]. En los últimos años, se ha comenzado a estudiar el semiconductor ZnO para posibles aplicaciones en espintrónica, debido a su excelente estabilidad y a que los dispositivos basados en espintrónica  poseen varias ventajas comparados con los de la electrónica convencional, tales como, no volatilidad, mayor velocidad en el procesamiento de datos, bajo consumo de energía [7].  Recientemente, ferromagnetismo a temperatura ambiente fue encontrado por Karmarkar et al. [8] en ZnO dopado con hierro y sintetizado mediante el método de reacción pirofórica química. Adicionalmente, cálculos por primeros principios, basado en la teoría del funcional de la densidad (DFT) [9] predicen ferromagnetismo en el ZnO dopado con metales de transición. Mera et al. [10] encuentran un comportamiento magnético atribuido al Mn en las películas delgadas Zn1-xMnxO, crecidas epitaxialmente mediante la técnica de deposición por láser pulsado. Estas propiedades magnéticas hacen del ZnO uno de los materiales más promisorios para aplicaciones en dispositivos de espintrónica. Por estas razones, en este trabajo, se estudian mediante DFT las propiedades estructurales, electrónicas y magnéticas de los compuestos MnO/ZnO debido a sus potenciales aplicaciones en espintrónica e inyectores de espín.

2. Metodo Computacional

Los cálculos se realizan dentro del marco de la Teoría del Funcional Densidad (DFT) y usando Ondas Planas Aumentadas Potencial Completo (FP-LAPW) como está implementado en el paquete WIEN2k [11]. Los efectos de correlación e intercambio de los electrones se tratan usando la aproximación de Gradiente Generalizado (GGA) de Perdew, Burke y Ernzerhof (PBE) [12]. En el método LAPW la celda se divide en dos tipos de regiones, las esferas atómicas centradas en los sitios nucleares y la región intersticial entre las esferas no superpuestas. Dentro de las esferas atómicas las funciones de ondas se reemplazan por funciones atómicas, mientras que en la región intersticial, la función se expande en ondas planas. La densidad de carga y los potenciales se expanden en armónicos esféricos hasta lmax=10 dentro de las esferas atómicas, y la función de onda en la región intersticial se expande en ondas planas con un parámetro de corte Kmax = 8/ Rmt, donde Rmt es el radio más pequeño de la esfera atómica en la celda unitaria y Kmax es la magnitud del vector k más grande de la red recíproca. Para asegurar convergencia en la integración de la primera zona de Brillouin se utilizaron 1600 puntos, lo que corresponde a 144 puntos k en la parte irreducible de la primera zona de Brillouin para la fase wurtzita. Las integrales sobre la zona de Brillouin se resuelven usando la aproximación especial puntos k de Monkhorst-Pack. La autoconsistencia se logra exigiendo que la convergencia de la energía total sea menor que 10^-4 Ry. Para la expansión del potencial en la región intersticial, se considera Gmax = 12. Los radios Muffin-tin fueron de 1.6 bohr para el N, 1.85 bohr para el Mn y 2.0 para el Zn. Los cálculos se realizan teniendo en cuenta la polarización de espín, debido a la presencia del átomo Mn. Para calcular la constante de red, el módulo de volumen y la energía de cohesión de la superred, los valores calculados se ajustan con la ecuación de estado de Murnaghan [13], ecuación (1).

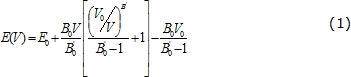
Donde B0 es el módulo de volumen, su primera derivada es B'0, V0 es volumen de equilibrio de la celda y E0 es la energía de cohesión. Con el fin de estudiar la estabilidad relativa de la superred  a una concentración, x de moléculas de ZnO y 1-x moléculas de MnO, se calculó la energía de formación. Para un compuesto ternario la energía de formación se define como la diferencia entre la energía total de la fase ternaria ZnxMn1-xO  y la energía  total de los compuestos binarios en sus estados bases, es decir, ZnO en wurtzita y MnO en NaCl,

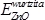
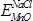
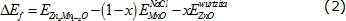
3.Resultados y Discusiones

3.1 Propiedades Estructurales

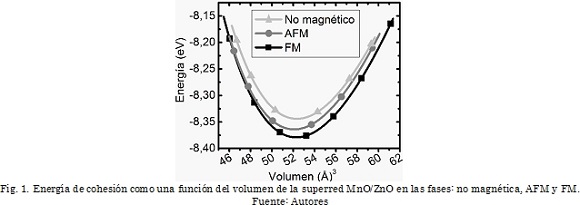
Con el fin de calcular las propiedades estructurales en el estado base, tales como, la constante de red (a0), el módulo de volumen (B0) y la energía de cohesión (E0) de los compuestos binarios ZnO y MnO y de la superred MnO/ZnO en estructura wurtzita, se calculó la energía total como una función del volumen, los resultados se ajustaron a la ecuación de estado de Murnaghan's. Adicionalmente, para determinar la fase magnética energéticamente más favorable, se calculó  la variación de la energía como una función del volumen en las fases: no magnética, antiferromagnética (AFM) y ferromagnética (FM). La Fig. 1 muestra las curvas energía-volumen de las tres fases calculadas para la superred MnO/ZnO. Como se puede ver en la Fig. 1 las curvas con energías más bajas corresponden a los estados  FM y AFM, siendo la diferencia de energía entre los estados FM y AFM (∆E = EFM - EAFM) de 0.011 eV, por lo tanto, la fase ferromagnética es la más favorable para superred. Nuestros resultados y varios resultados teóricos y experimentales son mostrados en la Tabla 1.

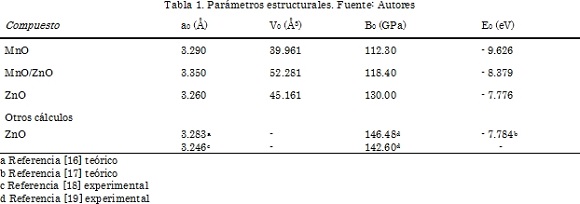
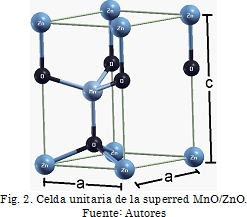
Los parámetros estructurales calculados (a0, B0, E0) en la estructura wurtzita del compuesto binario ZnO son bastante próximos a los resultados teóricos [referencias a y c] y está en buen acuerdo con resultados experimentales, debido a que difieren en menos del uno por ciento (1%) [Referencias c y d]. La estructura de la superred se obtiene colocando un átomo de Mn en la posición del Zn en la supercelda del ZnO. La Fig. 2 muestra la estructura cristalina de la superred obtenida después de la relajación estructural, la estructura obtenida es la estructura tetragonal p3m1(n° 156). Como se muestra en la Tabla 1, el valor del módulo de volumen de la superred MnO/ZnnO es alto, lo que confirma que es bastante rígida, haciéndola una buena candidata para posibles aplicaciones en dispositivos que deban funcionar a altas temperaturas, altas potencias y en recubrimientos duros.

Como se puede ver en la Tabla 1, las energías E0 en los estados base de los compuestos binarios ZnO y MnO son negativas, sin embargo, de acuerdo al resultado mostrado en la Tabla 2, el valor de la energía de formación de la superred  MnO/ZnO es positiva, por lo tanto, la superred es metaestable, esto implica que para poder crecerla es necesario suministrarle energía [14], [15]. El resultado obtenido para la energía de formación es importante, porque conociendo este valor se pueden mejorar las condiciones de crecimiento y por tanto, crecer superredes MnO/ZnO de buena calidad.

3.2 Propiedades Electrónicas y Magnéticas

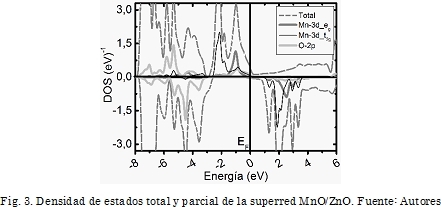
Las constantes de red de teóricas mostradas en la Tabla 1 se usaron para calcular la densidad de estado DOS de la superred MnO/ZnO. La Fig. 3 muestra la densidad de estado total (TDOS) y parcial (PDOS) de los orbitales que más contribuyen cerca del nivel de Fermi.

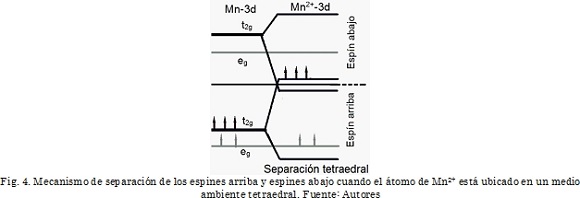
La TDOS muestra que la superred posee un comportamiento semimetálico y ferromagnéticos, debido a que en la banda de valencia cerca del nivel de Fermi, los espines mayoritarios (espines arriba) son metálicos y los espines minoritarios (espines abajo) son semiconductores. La superred posee una polarización de espín del 100% de los portadores de conducción en el estado base. Lo cual es un requerimiento de los inyectores de espín [20], esto sugiere que la superred puede ser eficientemente utilizada como inyectores de espín. La Fig. 3 muestra que en la banda de valencia cerca del nivel de Fermi, la densidad de espín arriba los espines mayoritarios están dominados por los estados Mn-3d principalmente y por los estados O-2p en menor contribución, los cuales atraviesan el Nivel de Fermi. Adicionalmente, de acuerdo con la teoría del campo cristalino, cuando un átomo de Mn reemplaza una átomo de Zn, el campo cristalino tetraedral generado por el ion de O, separa los cinco niveles  energéticos del átomo de Mn-3d en tres estados degenerados de alta energía t2g (dxy, dxz y dyz) y dos estados degenerados de baja energía eg (d_z² y d_x² -_y² ) [21]. Las propiedades magnéticas en la superred son atribuidas al átomo de manganeso en la configuración Mn2+; la Fig. 4 muestra la separación de los niveles del Mn-3d en espines mayoritarios (espín arriba) y espines minoritarios (espín abajo) debido al intercambio, se muestra la separación de los niveles doblemente degenerados eg y triplemente degenerados t2g cuando el manganeso Mn2+ está ubicado en un ambiente tetraedral, no se muestran los espines abajo porque de acuerdo con la densidad de estados DOS (Fig. 3) cerca del nivel de Fermi no hay contribución de espín abajo. El hecho de atribuir la configuración electrónica Mn2+ a la superred MnO/ZnO se puede entender de la siguiente manera. El átomos de Mn tiene siete electrones de valencia {con configuración electrónica [Ar]3d54s2}, cuando el Mn ocupa el sitio del Zn cede los dos electrones del orbital 4s^3+-. De los cinco electrones restantes del orbital 3d⁵ en el átomo de Mn dos ocupan el estado doblemente degenerado eg y dos electrones ocupan el estado triplemente degenerado t2g. Por tanto, en la superred los estados de espín mayoritarios Mn^3+-3d están completamente ocupados, como resultado, los cinco electrones se acoplan ferro-magnéticamente y producen un momento magnético total de 5 µβ/átomo-Mn. La superred posee un comportamiento ferromagnético y semimetálico. Un resultado similar fue obtenido por  Silvia Picozzi y Marjana Lezaic en su estudio por primeros principios de los semiconductores magnéticos diluidos grupo-IV [22].

Por otro lado, de acuerdo con la teoría Jhi et al. [23], la hibridación entre los estados metálicos Mn-3d y los electrones no metálicos O-2p que atraviesan el nivel de Fermi, resultan en un fuerte enlace covalente responsables de la alta rigidez de los compuestos ternarios permitidos.

4. Conclusiones

Reportamos cálculos por primeros principios de las propiedades estructurales, electrónica y magnéticas de la superred MnO/ZnO, usando el método ondas planas aumentadas y linealizadas potencial-completo (FP-LAPW), el marco de la teoría del funcional de la densidad y la aproximación gradiente generalizado (GGA). Se encontró que el valor del módulo de volumen de la superred es alto, por tanto, esta superred es rígida y es buena candidata para aplicaciones en dispositivos que deban trabajar altas temperaturas, altas potencias y en recubrimientos duros. Además, encontramos que la superred MnO/ZnO posee un comportamiento semimetálico con un momento magnético de  5 µβ por celda, el estado base ferromagnético proviene de la hibridación de los orbitales Mn-3d y O-2p que atraviesan el nivel de Fermi. Debido a estas propiedades esta superred es una buena candidata para potenciales aplicaciones en espintrónica e inyectores de espín.

5. Agradecimientos

Los autores agradecen al Centro de Investigaciones de la Universidad Distrital Francisco José de Caldas CUID, por el apoyo económico.

Referencias

[1] S. Limpijumnong and S. Jungthawan, “First-principles study of the wurtzite-to-rocksalt homogeneous transformation: A case of a low-transformation barrier," Phys. Rev. B, vol. 70, no. 5, p. 054104, Aug. 2004.         [ Links ]

[2] H. Wamg, C. Xie, W. Zhang, S. Cai, Z. Yang, and Y. Gui, “Comparison of dye degradation efficiency using ZnO powders with various size scales,” J. Hazard. Mater., vol. 141, no. 3, pp. 645-652, Mar. 2007.         [ Links ]

[3] S. Hong, T. JoS. Hong, T. Joo, W. Il Park, Y. H. Jun, and G.-C. Yi, “Time-resolved photoluminescence of the size-controlled ZnO nanorods,” Appl. Phys. Lett., vol. 83, no. 20, p. 4157, 2003.         [ Links ]

[4] J. Schulz, H. Hohenberg, F. Pflücker, E. Gärtner, T. Will, S. Pfeiffer, R. Wepf, V. Wendel, H. Gers-Barlag, and K.-P. Wittern, “Distribution of sunscreens on skin,” Adv. Drug Deliv. Rev., vol. 54, pp. S157-S163, Nov. 2002.         [ Links ]

[5] Y. D. L. J.Q. Xu Y.P. Chen and J. N. Shen, “Gas sensing properties of ZnO nanorods prepared by hydrothermal method,” J. Mater. Sci., vol. 40 (11), pp. 2919-2921, 2005.

[6] J. Zhou, N.J. Zhou, N. S. Xu, and Z. L. Wang, “Dissolving Behavior and Stability of ZnO Wires in Biofluids: A Study on Biodegradability and Biocompatibility of ZnO Nanostructures,” Adv. Mater., vol. 18, no. 18, pp. 2432-2435, Sep. 2006.         [ Links ]

[7] M. Kaminska, A. Twardowski, and D. Wasik, “Mn and other magnetic impurities in GaN and other III-V semiconductors - perspective for spintronic applications,” J. Mater. Sci. Mater. Electron., vol. 19, no. 8-9, pp. 828-834, Sep. 2008.         [ Links ]

[8] D. Karmakar, S. K. Mandal, R. M. Kadam, P. L. Paulose, A. K. Rajarajan, T. K. Nath, A. K. Das, I. Dasgupta, and G. P. Das, “Ferromagnetism in Fe-doped ZnO nanocrystals: Experiment and theory,” Phys. Rev. B, vol. 75, no. 14, p. 144404, Apr. 2007        [ Links ]

[9] M. H. F. Sluiter, Y. Kawazoe, P. Sharma, A. Inoue, A. R. Raju, C. Rout, and U. V Waghmare, “First Principles Based Design and Experimental Evidence for a ZnO-Based Ferromagnet at Room Temperature,” Phys. Rev. Lett., vol. 94, no. 18, p. 187-204, May 2005.         [ Links ]

[10] J. Mera, C. Córdoba, J. Doria, A. Gómez, C. Paucar, D. Fuchs, and O. Morán, “Structural and magnetic properties of Zn1-xMnxO nanocrystalline powders and thin films,” Thin Solid Films, vol. 525, pp. 13-19, Dec. 2012.         [ Links ]J. Mera, C. Córdoba, J. Doria, A. Gómez, C. Paucar, D. Fuchs, and O. Morán, “Structural and magnetic properties of Zn1-xMnxO nanocrystalline powders and thin films,” Thin Solid Films, vol. 525, pp. 13-19, Dec. 2012.

[11] K. Schwarz, P. Blaha, and S. B. Trickey, “Electronic structure of solids with WIEN2k,” Mol. Phys., vol. 108, no. 21-23, pp. 3147-3166, Nov. 2010.         [ Links ]

[12] J. P. Perdew, K. Burke, and M. Ernzerhof, “Generalized Gradient Approximation Made Simple,” Phys. Rev. Lett., vol. 77, no. 18, pp. 3865-3868, Oct. 1996.         [ Links ]

[13] M. F. D, “The Compressibility of media under pressure,” Proc. Natl. Acad. Sci. U.S.A, vol. 30 (9), pp. 244-247, 1944.         [ Links ]

[14] R. F. Zhang and S. Veprek, “Phase stabilities and spinodal decomposition in the Cr1-xAlxN system studied by ab initio LDA and thermodynamic modeling: Comparison with the Ti1-xAlxN and TiN/Si3N4 systems,” Acta Mater., vol. 55, no. 14, pp. 4615-4624, Aug. 2007.         [ Links ]

[15] S. H. Sheng, R. F. Zhang, and S.S. H. Sheng, R. F. Zhang, and S. Veprek, “Phase stabilities and thermal decomposition in the Zr1-xAlxN system studied by ab initio calculation and thermodynamic modeling,” Acta Mater., vol. 56, no. 5, pp. 968-976, Mar. 2008.

[16] X.-G. Xu, H.-L. Yang, Y. Wu, D.-L. Zhang, and Y. Jiang, “A first-principles study of the magnetic properties in boron-doped ZnO,” Chinese Phys. B, vol. 21, no. 4, p. 047504, Apr. 2012.         [ Links ]

[17] P. C. W. López and J. A. Rodríguez, “Estabilidad y estructura electrónica del ZnO,” Rev. Colomb. Física, vol. 43 (1), pp. 262-265, 2011.         [ Links ]

[18] S. K. Neogi, R. Karmakar, A. K. Misra, A. Banerjee, D. Das, and S. Bandyopadhyay, “Physical properties of antiferromagnetic Mn doped ZnO samples: Role of impurity phase,” J. Magn. Magn. Mater., vol. 346, pp. 130–137, Nov. 2013.         [ Links ]

[19] S. Desgreniers, “High-density phases of ZnO: Structural and compressive parameters,” Phys. Rev. B, vol. 58, no. 21, pp. 14102-14105, Dec. 1998.         [ Links ]

[20] M. E. C. Vargas-Hernández and R. Báez, “Half-metallic ferromagnetism of ZnxMn1-xO compounds: A first-principles study,” Comput. Condens. Matter, vol. 4, pp. 1–5, 2015.         [ Links ]

[21] X. Y. Cui, B. Delley, A. J. Freeman, and C. Stampfl, “Magnetic Metastability in Tetrahedrally Bonded Magnetic III-Nitride Semiconductors,” Phys. Rev. Lett., vol. 97, no. 1, p. 016402, Jul. 2006.         [ Links ]

[22] S. Picozzi and M. Ležaic, “Ab-initio study of exchange constants and electronic structure in diluted magnetic group-IV semiconductors,” New J. Phys., vol. 10, no. 5, p. 055017, May 2008.         [ Links ]

[23]S.-H. Jhi, J. Ihm, S. G. Louie, and M. L. Cohen, “Electronic mechanism of hardness enhancement in transition-metal carbonitrides,” Nature, vol. 399, no. 6732, pp. 132–134, May 1999.         [ Links ]