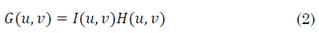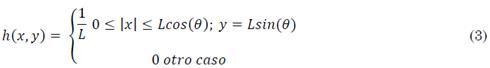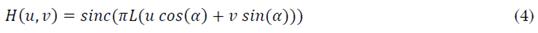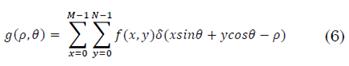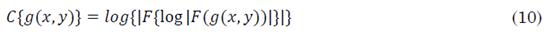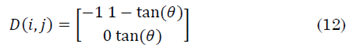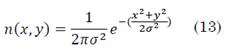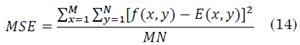1. INTRODUCCIÓN
La reconstrucción de la Función de Dispersión de Punto (PSF) debido a la difuminación causada por movimiento (motion blur) ha sido un tema de interés en diferentes áreas en los últimos años, como lo es en la oftalmología [1] y en las imágenes diagnósticas de ultrasonido [2]. También ha sido estudiado para la estimación de velocidades a partir de una única imagen [3], [4], [5], [6] y en la industria [7]. En los últimos años, muchas investigaciones se han realizado para identificar con mayor exactitud los parámetros de la PSF. Yitzhaky, planteó una metodología para la estimación del ángulo de la PSF por medio de un kernel direccional derivativo tangencial [8]. [9] estimaron el ángulo de la PSF por medio de la transformada de Radon en 2D aplicada sobre el logaritmo de la transforma de Fourier 2D. Además, estimaron la longitud de la PSF al identificar la distancia entre dos ceros sucesivos en el patrón generado por la transformada de Radon [9]. [10] realizaron la estimación del ángulo de la PSF por medio de la transformada de Hough sobre el logaritmo de la transformada de Fourier 2D [10]. Por otro lado, Rekleitis aplicó una familia de filtros adaptativos, como el filtro Gaussiano, sobre el logaritmo de la transformada de Fourier para la estimación del ángulo de la PSF [11]. Aquí se debe destacar que una de las técnicas más mencionadas en la literatura científica en el área del análisis de señales es el Cepstrum [12], [13], [14], [15]. Su dominio puede usarse para la separación de los componentes de la PSF de las componentes de la imagen. Alternativamente, Shah y Dalal formularon una metodología para estimar la longitud y el ángulo de la PSF en el dominio del Cepstrum al que denominaron Cepstrum modificado [16], [17]. También se han usado técnicas de aprendizaje de máquina como las Máquinas de Soporte Vectorial Multiclase (SVM) y Redes Neuronales Artificiales (ANN) para clasificar algunas características de las imágenes para longitudes diferentes de la PSF [18], [19]. Por último, existe un conjunto de técnicas alternativas emergentes basadas histogramas de gradientes orientados [20] y estadística de la imagen [21]. En este artículo, se evalúan con mayor detalle y rigor las técnicas más destacas en el estado del arte para la identificación de los parámetros de la PSF relacionada con la difuminación por movimiento lineal uniforme, considerando el Ruido Blanco Aditivo Gaussiano (AWGN) y sus tiempos de ejecución. Estos aspectos no han sido abordados con rigurosidad en la literatura científica encontrada por los autores.
1.1 Modelo de degradación de la imagen
La difuminación (blur) es una forma de reducción del contenido de alta frecuencia de la imagen que puede ser causado, entre otras causas, por imperfecciones en la lente, turbulencia atmosférica o por el movimiento relativo entre la escena y la cámara (motion blur). Este último tipo de degradación mecánica se puede presentar en forma de translación, rotación o como un cambio de escala [22].
La base de formación de una imagen puede ser explicada mediante la Función de Dispersión de Punto (PSF), la cual puede entenderse como la Función de Transferencia del Sistema Óptico. Esta indica cómo una fuente puntual, monocromática, y coherente de luz resulta en un punto difuminado en el dominio del espacio al pasar por el sistema (Respuesta a la Función Impuso Unitario). Es decir, la imagen resultante real no es necesariamente una copia perfecta de la fuente de luz puntual, sino que esta presenta una difuminación [23]. La degradación de una imagen se puede modelar por (1):
Donde n(x,y) es el ruido y * es la operación de convolución entre la imagen no degradada I(x,y) y la PSF h(x,y). De esta manera, se tiene como resultado la imagen degradada g(x,y) por la Función de Dispersión de Punto h(x,y). En esta investigación, la PSF es la Función de Transferencia que modela la difuminación (motion blur) que afecta a la imagen.
1.2 Estimación de los parámetros
A partir de la definición de una imagen degradada en el dominio del espacio, como se mostró en (1), el modelo se puede expresar como una multiplicación punto a punto en el dominio de frecuencia. Por lo anterior, se puede obtener una definición análoga en el dominio de la frecuencia sin considerar el ruido, como se muestra en (2).
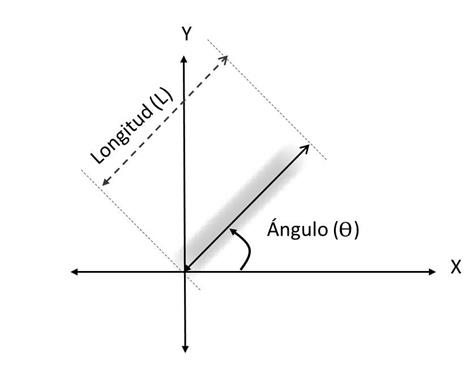
Donde G(u,v) es el resultado de la multiplicación punto a punto en frecuencia (Transformada de Fourier en dos dimensiones) de la imagen no degradada I(u,v) con la Transformada Óptica de Fourier (OFT) H(u,v). Para calcular los parámetros de la PSF se deben considerar las variables como se muestra en la Fig. 1.
Cuando el objeto se mueve a una velocidad relativa constante durante la exposición de la cámara, se produce la difuminación por movimiento. En la escena mostrada en la Fig. 1 se observa una estela de baja energía que contiene información del movimiento relacionada con la longitud de la estela L y el ángulo θ de la misma [24]. La PSF para el movimiento lineal uniforme se puede modelar de forma espacial como (3).
La respuesta en frecuencia de h(x,y), dada por la Transformada de Fourier de la función Rectangular, está dada por la función SINC que se muestra en (4).
En conclusión, si se transforma una imagen degradada por movimiento uniforme al dominio de la frecuencia (Espectro de Potencia de Fourier), es posible observar el efecto de la difuminación sobre la imagen e identificar los parámetros de la PSF. En la Fig. 2. Se puede observar que las líneas paralelas dominantes en el espectro de Fourier de la imagen son ortogonales al ángulo de la difuminación, mientras, la longitud está ligada a la distancia entre las líneas (distancia entre lóbulos laterales de la función SINC). Cuanto más cercanas estén las líneas entre sí, mayor es la longitud de la difuminación [24], [10]. Debido a lo mencionado anteriormente, la tarea de estimación del ángulo se encuentra en la identificación de la orientación de las líneas, y la estimación de la longitud está relacionada con la identificación de la distancia entre ellas. Sí se conoce el ángulo y la longitud de la PSF es posible reconstruir la imagen original por medio de la deconvolución entre la imagen con degradación y la PSF estimada [25], [21]. A manera de ejemplo, la Fig. 3muestra el efecto de la degradación sintética sobre la imagen de Lenna (Fig. 3(a)) en el dominio de la fre-cuencia.
Fuente: autores.
Fig. 2 Función SINC (4). (a) Muestra como calcular el ángulo de la PSF a partir del patrón de Fourier. (b) Ilustra el patrón rotado con un trazo de la Función Sinc (4) sobre la imagen.

Fuente: autores.
Fig. 3 Efectos de la degradación sobre la imagen de Lenna. (a) Imagen original de Lenna no degradada. (b) Imagen de Lenna degradada con una difuminación de 30 píxeles a 50 grados. (c) Espectro de Potencia de Fourier de la imagen original. (d) Espectro de Potencia de Fourier de la imagen degradada. Fuente: autores.
2. METODOLOGÍA
2.1 Estimación del ángulo de la PSF
En esta sección se mostrarán los métodos seleccionados para la identificación del ángulo de la PSF, como: Transformada de Hough, Transformada de Radon, Filtro Adaptativo Gausiano, Filtro Adaptativo Gabor y Cepstrum 2D.
2.1.1 Transformada de Hough
El espacio de la transformada de Hough está basado en la representación Hessiana de una línea (5):
Donde (x,y) son las coordenadas de un punto de la línea a considerar, θ es el ángulo formado entre la línea y un trazo perpendicular de longitud ρ que inicia desde el origen cartesiano hasta la línea de interés. En el espacio transformado de Hough se localiza el ángulo θ como el pico o el punto más brillante.
Para obtener el ángulo de la dirección de la PSF, primero, se debe realizar la transformada de Fourier de la imagen. Seguidamente, sobre el logaritmo de la transformada de Fourier de esta, se realiza la transformada de Hough para obtener la dirección de las líneas paralelas dominantes. Por último, el ángulo de la PSF está dado por 90-θ en grados [10], [26]. La Fig. 4 muestra el resultado de aplicar la transformada de Hough sobre el espectro de Fourier con una imagen degradada con difuminación sintética orientada a 35 grados.

Fuente: autores.
Fig. 4 Transformada de Hough sobre el Espectro de Potencia de Fourier de la imagen de Lenna degradada. (a) Espectro de Potencia de Fourier de Lenna degradada con una longitud de 25 píxeles a un ángulo de 35 grados. (b) Espectro de Potencia de Fourier binarizado con un umbral de 0,6. (c) Transformada de Hough del espectro binarizado.
2.1.2 Transformada de Radon
La transformada de Radon, para este caso, es la proyección del Espectro de Fourier en dos dimensiones sobre una línea rotada a diferentes ángulos θ. Este último parámetro tiene igual significado que el indicado en la transformada de Hough. Cada una de las proyecciones sobre las líneas está representada en la transformada de Radon como picos, que determinan la ubicación de las líneas originales de la imagen; en otras palabras, la transformada de Radon es una integral de línea [9]. La transformada de Radon en el dominio discreto en 2D está definida por (6).
Donde f(x,y) es la imagen, M es el número de columnas de la imagen, N es el número de filas de la imagen, δ es el delta de Dirac, θ es el ángulo formado entre la línea y una línea perpendicular que inicia desde el origen cartesiano hasta la línea, y ρ es la distancia de la línea perpendicular. Para determinar el ángulo de la PSF con la transformada de Radon, primero, se debe realizar la transformada de Fourier de la imagen degradada. Posteriormente, se realiza la transformada de Radon sobre el logaritmo del espectro. El punto más brillante (ρ,θ) en la matriz resultante de la transformada de Radon está relacionado con el ángulo θ de la dirección de las líneas paralelas dominantes [27]. La Fig. 5 muestra el resultado de aplicar la Transformada de Radon sobre el espectro de Fourier de una imagen degradada con difuminación sintética por movimiento orientada a 50 grados
2.1.3 Filtros adaptativos
Los filtros adaptativos son comúnmente usados para la detección de bordes, compresión de imágenes, análisis de texturas, entre otras aplicaciones en el área del Procesamiento Digital de Imágenes (PDI) [28]. Rekleitis expuso un método para determinar la orientación de la PSF a partir de la rotación de un filtro Gaussiano sobre el logaritmo del espectro de Fourier [11]. Para determinar la orientación de las líneas, se promedia la respuesta de energía del filtro sobre el Espectro de Potencia de Fourier de la imagen degradada en cada ángulo; al final, la orientación de las líneas determinantes del ángulo θ de la PSF está determinada en el ángulo donde se haya obtenido la respuesta de energía más alta. El kernel del filtro adaptativo Gaussiano está modelado por (7). Donde; FG representa el filtro, k a , k b y k c son funciones de interpolación, G 2a , G 2b y G 2c son parámetros de la segunda derivada de la función gaussiana.
De forma análoga, el kernel de la parte real del filtro adaptativo Gabor está modelado por (8). Donde; ϕ es la fase, FG es el filtro,  es una función de interpolación, λ es la longitud de onda y K es un parámetro de escala del filtro de Gabor. Para detallar el desglose de los términos de la ecuación del filtro Gaussiano y Gabor, refiérase a [11], [28], [29], [30].
es una función de interpolación, λ es la longitud de onda y K es un parámetro de escala del filtro de Gabor. Para detallar el desglose de los términos de la ecuación del filtro Gaussiano y Gabor, refiérase a [11], [28], [29], [30].
2.1.4 Cepstrum 2D
El dominio del Cepstrum es utilizado para la separación de las componentes de la degradación de la imagen [13]. La transformada de Cepstrum está definida por (9).
Donde g(x,y) es la imagen con difuminación, F es la transformada de Fourier, log es el logaritmo natural del valor absoluto de la transformada de Fourier y F -1 es la transformada inversa de Fourier. Por otro lado, los investigadores Shan y Dalal [16], [17] propusieron un dominio basado en Cepstrum al que denominaron “Cepstrum modificado”, que está definido por (10).
Con la imagen degrada en el dominio del Cepstrum, se realiza la técnica de bit plane slicing para extraer el cuarto bit y así binarizar la imagen. El ángulo en el dominio del Cepstrum 2D puede ser estimado a partir de la transformada de Hough sobre la Fig. 6(c). Por último, el ángulo de la PSF está dado por 180-θ en grados. Los autores presentados en [16], [17] usaron para la binarización el cuarto bit, pero, en este caso, se usó el sexto bit en la binarización, ya que, se obtuvo un mejor resultado.
2.2 Estimación de la longitud de la PSF
En esta sección se mostrarán algunos métodos para la identificación de la longitud de la PSF, como: Función de Auto Correlación (ACF), Transformada de Radon y el Cepstrum en una dimensión.
2.2.1 ACF
La correlación es la relación entre dos (o más) señales; esta se puede usar para determinar la dependencia entre las señales que intervienen. De forma análoga, la Función de Auto Correlación (ACF) cuantifica cuanto se relacionan dos muestras de un mismo proceso. La función de auto correlación está definida por (11):
En este caso, 𝐼(𝑖) es un vector con la misma orientación de la difuminación, I( i+ τ ) es una versión del mismo vector pero con desplazamiento Ƭ. El valor de Ƭ que maximice la función de auto correlación corresponde a la longitud de la PSF [31].
Para determinar la longitud de la PSF a partir de la función de auto correlación se debe realizar la convolución entre el kernel derivativo tangencial propuesto en [8] con la orientación θ sobre la imagen degradada para obtener la derivada direccional. Luego se ubica el ángulo para el cual la energía es mínima. Posteriormente se rota la imagen y se realiza la función de auto correlación sobre cada fila y se promedia. Por último, se ubica el punto donde el valor de la señal sea mínimo para identificar la longitud de la PSF. La ecuación (12) presenta el kernel derivativo tangencial usado para hallar la derivada direccional de la imagen.
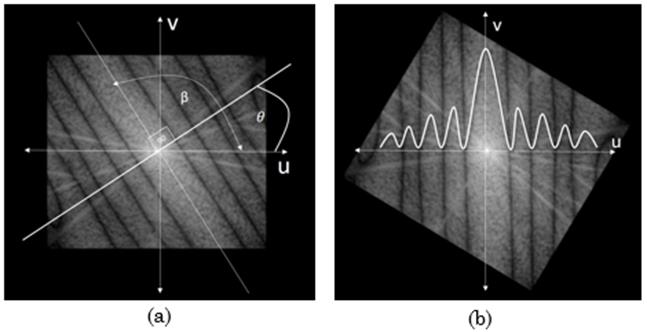
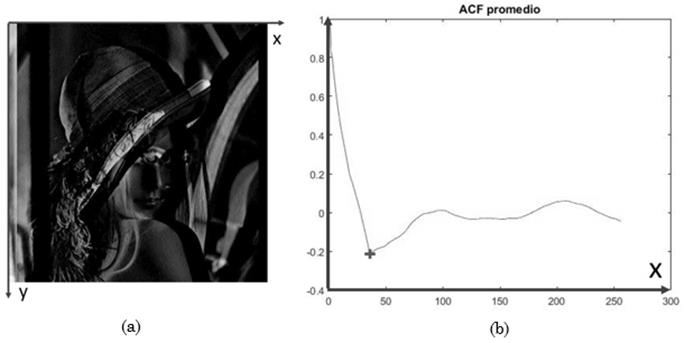
La Fig. 7 muestra el efecto del kernel derivativo tangencial sobre una imagen degradada.
Fuente: autores.
Fig. 7 Método de ACF para esitmación dela longitud. (a) Convolución entre el kernel derivativo tangencial con orientación cero sobre Lenna degradada con una longitud de 35 píxeles a un ángulo de cero grados. (b) Promedio normalizado de la función de auto correlación de cada una de las filas de la imagen (a).
2.2.2 Transformada de Radon
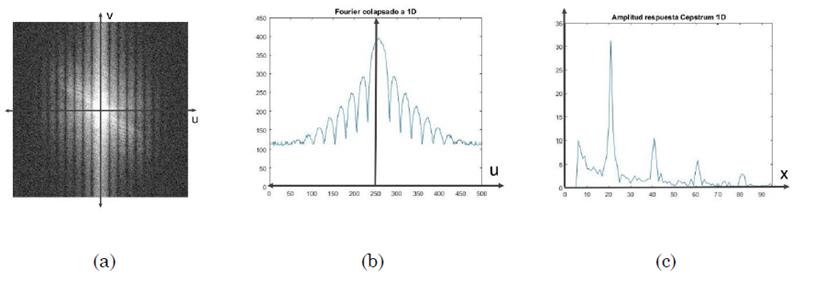
La aproximación a la longitud de la PSF a partir de la transformada de Radon, propone, en primera instancia, determinar la orientación de las líneas del espectro a partir de la transformada de Radon. Posteriormente, rotar la imagen con el ángulo estimado, luego, colapsar el Espectro de Potencia de Fourier 2D sobre el eje u para obtener una representación en una dimensión (1D). Por último, identificar los mínimos relativos a partir de la derivada del espectro 1D y promediar la distancia entre ellos para estimar la longitud de la PSF [32], [33]. La Fig. 8 muestra la relación existente entre las zonas oscuras y los mínimos relativos con orientación de cero grados.
2.2.3 Cepstrum 1D
Para estimar la longitud de la PSF a partir del dominio del Cepstrum, se requiere, determinar la orientación de las líneas del Espectro de Potencia de Fourier por medio de la transformada de Radon. Luego, rotar la imagen con la orientación estimada, para después, colapsar el espectro en 2D sobre el eje u para obtener el espectro de Fourier 1D. Posteriormente, se realiza la transformada de Fourier 1D sobre la señal y se halla el valor absoluto para evitar puntos negativos, en este punto se encuentra la señal en el domino del Cepstrum en 1D; se aplicó una ventana a la señal desde los primeros cinco valores para atenuar el efecto de los contenidos de baja frecuencia, al final, la longitud de la PSF está dada por el punto donde se encuentre el máximo valor de la señal [34]. En la Fig. 9 se puede apreciar la forma de la señal en el dominio del Cepstrum en 1D.
2.3 Evaluación de técnicas
Para la evaluación de las técnicas se utilizó la base de datos de la Universidad del Sur de California (USC-SIPI) [35], de la cual se tomaron 20 imágenes con una resolución de 512x512 con 8 píxeles de profundidad. Esta base de datos es reconocida y ha sido utilizada por más de 30 años en la evaluación de técnicas de procesamiento de imágenes, debido a que las imágenes cuentan con altos contenidos de alta y baja frecuencia y es posible realizar trazabilidad sobre ellas para la reproducción de los experimentos. Mediante su uso, se realizó la evaluación de técnicas de análisis en el dominio del espacio y la frecuencia para la estimación del ángulo y la longitud de PSF. La Fig. 10 muestra las imágenes seleccionadas de la base de datos usadas para la investigación.

Fuente: [35].
Fig. 10 Imágenes seleccionadas de la base de datos USC-SIPI usada para los experimentos.
Para la estimación del ángulo, se evaluaron las siguientes técnicas: Transformada de Hough, Transformada de Radon, Filtro Adaptativo Gaussiano, Filtro Adaptativo Gabor y Cepstrum 2D. Para realizar esta estimación se estableció la longitud de la PSF de 55 píxeles y se hicieron variaciones del ángulo desde uno hasta noventa grados, con incrementos de un grado.
Para la estimación de la longitud, se evaluaron las técnicas: Función de Auto Correlación, Transformada de Radon y Cepstrum en una dimensión. Debido a que la longitud máxima del motion blur que se puede obtener es el valor del tamaño de la imagen (512), se estableció el límite de longitud de 95 píxeles para la experimentación, ya que este valor es mucho menor que el tamaño de la imagen. Para realizar la estimación de la longitud se estableció el ángulo de la PSF en cero grados y se hicieron variaciones desde cinco hasta noventa y cinco píxeles con incrementos de un píxel. Luego se realizó un análisis con los errores absolutos promedio de cada una de las técnicas para la estimación del ángulo y la longitud de la difuminación, además, se elaboró un estudio comparativo entre las técnicas para determinar cuál de ellas presentaba mejores resultados respecto a los parámtros definidos anteriormente.
El algoritmo 1 presenta el paso a paso de la metodología usada para la evaluación de las técnicas para la estimación del ángulo y la longitud de la PSF.
Algoritmo 1. Metodología para la evaluación de las técnicas para la estimación del ángulo y la longitud de la PSF.
Paso 1. Para cada una de las 20 imágenes de la base de datos USC-SIPI.
Paso 2. Repetir desde 𝜃=1 hasta 90, con incremento de un grado.
{
Aplicar difuminación sintética a la imagen con L= 55 píxeles a un ángulo 𝜃.
Evaluar cada método presentado para ángulo.
Computar el error absoluto.
}
Paso 3. Leer nuevamente la imagen.
Paso 4. Repetir desde 𝐿=5 hasta 95, con incremento de un píxel.
{
Aplicar difuminación sintética a la imagen con 𝜃=0 a una longitud L.
Evaluar cada método presentado para longitud.
Computar el error absoluto.}
Paso 5. Realizar una comparación de los resultados de los métodos
2.4 Evaluación de robustez al ruido
El ruido puede estar presente en una imagen desde el mismo instante de captura de la imagen por la cámara debido a sensores defectuosos, errores en la transmisión de la señal por problemas en los canales de comunicación o el ruido térmico generado por los circuitos de la cámara. En esta investigación se considera el efecto del ruido sobre los métodos evaluados. Siendo el Ruido Aditivo Blanco Gaussiano (AWGN), el tipo de ruido más común en aplicaciones prácticas se seleccionó como modelo de ruido para evaluar la robustez de las técnicas frente al ruido [34]. Como el ruido mencionado es de tipo aditivo, se retoma (1).
Donde g(x, y) es la imagen degradada, h(x, y) es la PSF y n(x, y) es el ruido aditivo sobre la imagen. Para este caso, el ruido añadido a la imagen es el Ruido Aditivo Blanco Gaussiano (AWGN) presentado en (13):
Donde n(x, y) es el AWGN, x y y son puntos de la imagen y σ es la desviación estándar del ruido. Por facilidad en el manejo de los datos, el ruido se presenta como una relación señal a ruido, la cual es una medida que estima la calidad de una imagen comparada con la imagen no degradada; entre más alta la relación, el ruido tiene una menor intensidad. La calidad de una imagen se mide a partir del error medio cuadrático (MSE), cuya expresión matemática se presenta en (14).
Donde f(x, y) es la imagen base y E(x, y) es la imagen con ruido, M y N son las columnas y las filas de las imágenes. Debido a que el Error Medio Cuadrático (MSE) depende del escalamiento de la intensidad de la imagen, esta relación es expresada en forma de una función logarítmica en unidades de decibeles para tratar de mantener una escala adecuada [36]. En (15) se presenta la conversión a decibles del MSE.
Donde PSNR es la Relación Señal a Ruido Pico de la imagen en decibeles y MSE es el error medio cuadrático obtenido en (14). Para estimar la robustez al ruido de las técnicas, se degradaron las imágenes de prueba con AWGN en un intervalo de 20dB a 36dB con incrementos de 2dB. Una vez más, se evaluaron las técnicas para la estimación del error promedio del ángulo y la longitud en presencia del ruido.
El algoritmo 2 presenta el paso a paso de la metodología usada para la evaluación de las técnicas para la estimación del ángulo y la longitud de la PSF presencia del ruido aditivo blanco gaussiano.
2.5 Tiempos de ejecución
Para estimar el tiempo promedio de ejecución de los métodos, se tomaron 100 iteraciones de cada algoritmo con una longitud de 55 píxeles y un valor de ángulo de 45 grados sobre la imagen Lenna como referencia. Todos los algoritmos realizados en esta investigación se ejecutaron sobre el programa MATLAB 2015a, en un equipo de cómputo de 64bits, 2GB de RAM con Windows 7 como sistema operativo y procesador Core i3. El algoritmo 3 presenta el paso a paso de la metodología usada para la evaluación de las técnicas para la estimación del tiempo de procesamiento.
Algoritmo 2. Metodología para la evaluación de las técnicas para la estimación del ángulo y la longitud de la PSF en presencia del ruido aditivo blanco gaussiano
Paso 1. Para cada una de las 20 imágenes de la base de datos USC-SIPI.
Paso 2. Repetir desde θ=1 hasta 90, con incremento de un grado.
{
Aplicar difuminación sintética a la imagen con L= 55 píxeles a un ángulo θ.
Repetir desde PSNR=20dB hasta 36dB, con incremento de 2dB.
{
Añadir ruido a la imagen degradada.
Evaluar cada método presentado para ángulo.
Computar el error absoluto.
}
}
Paso 3. Leer nuevamente la imagen.
Paso 4. Repetir desde L=5 hasta 95, con incremento de un píxel.
{
Aplicar difuminación sintética a la imagen con θ=0 a una longitud L.
Repetir desde PSNR=20dB hasta 36dB, con incremento de 2dB.
{
Añadir ruido a la imagen degradada.
Evaluar cada método presentado para longitud.
Computar el error absoluto.
}
Paso 5. Realizar una comparación de los resultados de los métodos.
Algoritmo 3. Metodología para la evaluación de las técnicas para la estimación del tiempo de procesamiento.
Paso 1. Leer imagen.
Paso 2. Aplicar difuminación sintética a la imagen con L= 55 píxeles y θ=45 grados.
Paso 3. Repetir desde i=1 hasta 100.
{
Iniciar toma de medidas.
Evaluar cada método presentado para ángulo y longitud.
Finalizar toma de medidas.
}
Paso 4. Promediar los tiempos de ejecución de cada una de las iteraciones de los métodos.
3. RESULTADOS Y DISCUSIÓN
Los resultados obtenidos en cada una de las pruebas para la estimación del ángulo y la longitud de la difuminación se mostrarán en la Fig. 11, 12, y 13.

Fuente: autores.
Fig. 11 Error absoluto promedio en grados para los métodos de filtros adaptativos Gaussiano, Gabor y Hough para la estimación del ángulo de la PSF.
Fuente: autores.
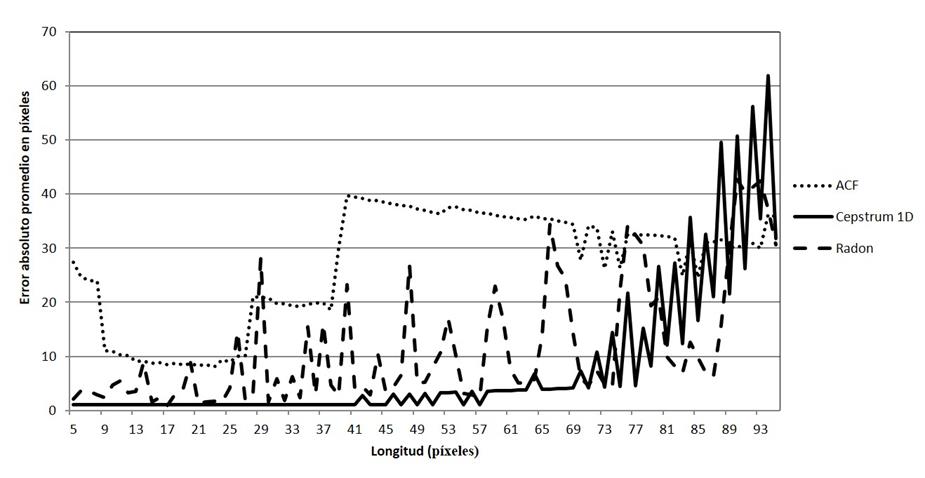
Fig. 13 Error absoluto promedio en píxeles para la estimación de la longitud en imágenes sin ruido.
En la Fig. 11 se puede apreciar que para las imágenes sin ruido los métodos de Hough y el filtro adaptativo Gabor tienen errores inferiores a 2 grados. Pero, el método de Hough presenta un pico en 90 grados que provoca un aumento en su error absoluto promedio.
En la Fig. 12 se aprecia que el método de Radon y Cepstrum 2D tienen resultados muy similares. Estos presentan un error absoluto promedio inferior a dos grados en la estimación del ángulo en todo el rango analizado; adicionalmente, ambos presentan un error absoluto promedio considerable en los primeros ángulos, lo que provoca un aumento en su error. La razón por la cual algunos de los métodos tienen dificultades en 0 y en 90 grados, es porque al momento de realizar la transformada de Fourier de la imagen, se presenta una alta energía en el centro de la imagen debido a los bordes de la misma y llega tener un mayor peso que los demás contenidos de energía de la imagen. Esto se aprecia como una cruz brillante sobre y hacia el centro del espectro de Fourier, aunque se atenúa mediante el ventaneo Hanning.
En la Fig. 13 se puede apreciar que el método con mejor estimación es Cepstrum 1D. Sin embargo, se hace evidente un aumento en el error cuando aumenta la longitud de la difuminación. Lo anterior es debido a la dificultad de ubicar los ceros entre las líneas paralelas en el espectro de Fourier a medida que aumenta la longitud de la difuminación por movimiento, tal y como se ha explicado.
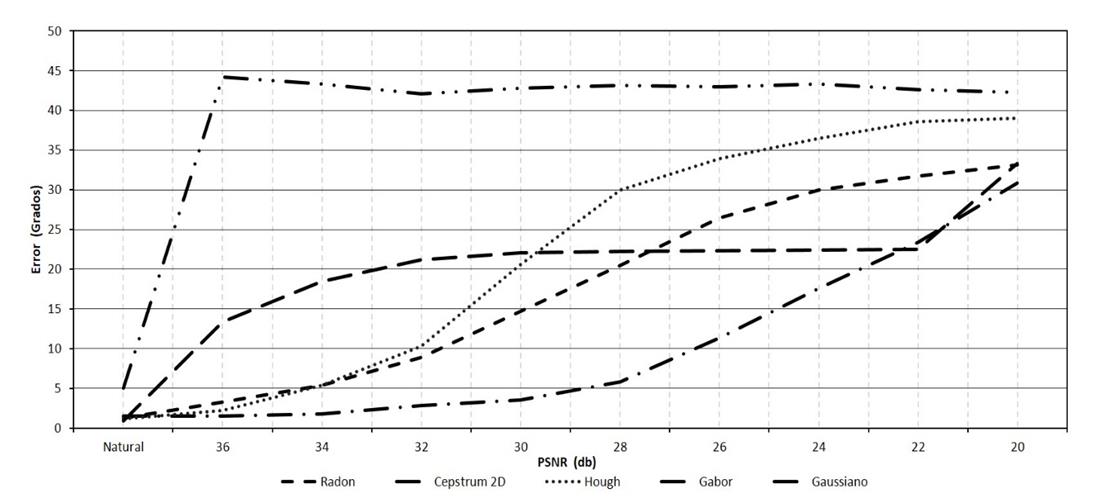
En la Fig. 14 se realiza una comparación de los métodos para la estimación del ángulo en presencia del Ruido Aditivo Blanco Gaussiano (AWGN), en la cual se puede observar que el método con mayor robustez para la estimación del ángulo es el Cepstrum 2D, con un error absoluto promedio inferior a 5 grados con una relación señal a ruido de 30dB.
Fuente: autores.
Fig. 14 Error absoluto promedio en grados para la estimación del ángulo en imágenes afectadas por ruido.
En la Fig. 13 se puede apreciar que el método con mejor estimación es Cepstrum 1D. Sin embargo, se hace evidente un aumento en el error cuando aumenta la longitud de la difuminación. Lo anterior es debido a la dificultad de ubicar los ceros entre las líneas paralelas en el espectro de Fourier a medida que aumenta la longitud de la difuminación por movimiento, tal y como se ha explicado.
En la Fig. 14 se realiza una comparación de los métodos para la estimación del ángulo en presencia del Ruido Aditivo Blanco Gaussiano (AWGN), en la cual se puede observar que el método con mayor robustez para la estimación del ángulo es el Cepstrum 2D, con un error absoluto promedio inferior a 5 grados con una relación señal a ruido de 30dB.
En la Fig. 15 se realiza una comparación de los métodos para la estimación de la longitud en presencia del Ruido Aditivo Blanco Gaussiano (AWGN), en la cual se puede observar que el método con menor error es la técnica de Radon, con un error absoluto promedio inferior a 20 píxeles con una relación señal a ruido de 28dB. No Obstante, se debe destacar que cuando la imagen no presenta ruido, el mejor método para la estimación de la longitud es el Cepstrum 1D con un error absoluto promedio inferior a 8 píxeles.

Fuente: autores.
Fig. 15 Error absoluto promedio en píxeles para la estimación de la longitud en imágenes afectadas por ruido.
En la Fig. 16 se realiza una comparación del tiempo de ejecución de los métodos para la estimación del ángulo. En la cual se puede observar que el método con el que se obtuvo un resultado en el menor tiempo es la técnica del Hough.
En la Fig. 17 se realiza una comparación del tiempo de ejecución de los métodos para la estimación de la longitud. Se puede observar que el método con el que se obtuvo un resultado en el menor tiempo es la técnica de Radon.
4. CONCLUSIONES
En este trabajo se introdujeron algunas técnicas representativas para la estimación de los parámetros de la PSF del desenfoque por movimiento lineal. Los resultados demuestran que el método que presentó el menor Error Absoluto Promedio para la estimación del ángulo es el Filtro Adaptativo de Gabor con un error promedio de 0,84 grados. No obstante, el método de Cepstrum 2D mantuvo un error promedio de 1 grado en el intervalo de 5 a 90 grados con un tiempo de ejecución inferior a 0,1 segundos. De igual forma, esta última es la técnica más tolerante en presencia del Ruido Aditivo Blanco Gaussiano (AWGN) para la estimación del ángulo con un error promedio en 30dB de 3,54 grados. De forma análoga, se evidenció que el método que presentó el menor error para la estimación de la longitud es el Cepstrum 1D con un error promedio de 8,03 píxeles con un error estable de menos de 5 píxeles en el intervalo de 5 a 60 píxeles. Igualmente, se observó que la técnica que presentó con mayor tolerancia al ruido para la estimación de la longitud de la PSF en presencia del Ruido AWGN es la Transformada de Radón con un error promedio en 28dB de 17,69 píxeles. Por último, la técnica que presentó menor tiempo de ejecución para la estimación del ángulo es Hough con un tiempo de 0,019 segundos y para la estimación de la longitud es la transformada de Radon con un tiempo de 0,0003 segundos. Por lo anterior, los autores recomiendan hacer uso de una técnica híbrida que realice el Cepstrum 2D para determinar el ángulo y el método del Cepstrum 1D para determinar la longitud de la PSF. Esta puede utilizarse, entre otras aplicaciones, para la restauración de la imagen degrada por movimiento, aunque que se encuentra fuera del alcance de este trabajo. Todos los métodos evaluados presentan importantes problemas de exactitud en la estimación del ángulo y la longitud en presencia de ruido. Por lo anterior, los autores consideran que se debe ahondar en el estudio de nuevas técnicas que resulten más tolerantes a sus efectos de degradación aún más evidentes si se trabaja con imágenes reales.