1. INTRODUCTION
Turning is one of the most common and useful machining operations performed in factories. Several studies have been developed to improve the machinability of materials and estimate the various cutting parameters using different modeling and optimization techniques to obtain the best machining characteristics (e.g., surface roughness, tool wear, and cutting forces).
Cutting forces are an important variable in machining, as they could indicate excessive wear of the cutting tool. This, in turn, negatively influences the surface roughness of the machined workpiece, its productivity and energy consumption, and the costs associated with the process. In addition, cutting forces are usually employed to calculate the energy consumed during the cutting process, an aspect of great relevance today. However, little research has been conducted to optimize the specific energy consumption in the high-speed turning of medium carbon steel.
In [1], Schulz discussed the advantages of High-Speed Machining (HSM). However, the author also found that one of its unwanted effects is that the tool wear rate often increases.
Likewise, the cutting forces, operation stability, cutting power, and energy consumption in the machining process could also increase.
In recent years, many renowned universities, companies, and international organizations have conducted extensive research on the energy consumption of machine tools [2]. In addition, several researchers have used different optimization techniques to determine the optimal cutting conditions for machining operations, with the aim of minimizing cutting forces and energy consumption. Nevertheless, studies into the high-speed turning of plain carbon steel using different cutting tool materials are unusual.
In [3], tool wear was examined using up to an intermediate cutting speed. Denkena et al.[4] evaluated the changes in chip formation, cutting forces, machining energy consumption, and cutting temperature when significantly increasing the cutting speed.
Nonetheless, these authors did not consider the optimization of cutting parameters in their study. Lin [5] assessed flank wear at different cutting speeds and feed rates when turning AISI 1055 steel (AISI is acronym of the American Iron and Steel Institute).
Davies et al. [6] calculated temperature distributions during the cutting of AISI 1045 steel for a variety of cutting parameters. Iqbal et al. [7] studied the tool-chip contact interface at different turning speeds (from conventional to high speeds) using uncoated cemented carbide inserts. They evaluated the effects of cutting speed on tool rake face contact length, contact area, friction, and chip compression ratio [8]. Later, the same authors investigated the variations in chip compression ratio and contact length at different undeformed chip thickness values [9]. However, they failed to include cutting forces and machining energy consumption.
Moreover, Quan et al. [10] analyzed the influence of cutting speed on cutting heat flux and distribution during the machining of plain carbon steel. Stanford et al. [11] examined the effect of some cutting fluids on tool wear, cutting force, and cutting temperature using up to an intermediate cutting speed. Diniz et al. [12] assessed the effect of coolant pressure on tool life at an intermediate cutting speed. Adesta et al. [13] investigated the effects of negative rake angle on flank wear and surface roughness. Although these authors developed their tests in the high-speed cutting field, they did not analyze cutting energy consumption.
Ozlu et al. [14] performed some high-speed turning experiments using inserts with different rake angles. They calculated the friction coefficient, cutting forces, and total contact length, but they did not consider the optimization of cutting parameters.
Özel et al. [15] examined the impact of insert geometry on cutting forces and surface roughness using intermediate cutting speeds. In addition, these authors used a neural network model to predict surface roughness. For their part, Rajemi et al. [16] assessed the optimum tool life for a minimum energy consumption taking into account the energy budget. However, they considered intermediate cutting speeds. Although Hernández et al.[17] analyzed the effect of removed metal volume rate on flank wear during the high-speed turning of AISI 1045 steel, they did not consider cutting forces nor machining energy consumption in their study.
Furthermore, Stachurski et al. [18] evaluated the effect of insert geometry on cutting force during dry and wet turning. Later, Hernández et al. [19] studied the resultant cutting force variation using HSM. Nevertheless, these two studies did not consider the optimization of cutting parameters.
Qasim et al. [20] optimized the machining parameters over a wide range of cutting speeds and two cutting tool materials to minimize temperature and cutting forces using a Taguchi design and Analysis of Variance (ANOVA). Their study revealed that the most significant factors for cutting forces are feed rate and depth of cut, even though it did not consider energy consumption.
Rahim et al. [21] found that cutting temperature and force with the Minimum Quantity Lubrication (MQL) technique were lower than with dry turning. However, they did not consider the optimization of cutting parameters.
For their part, Xie et al. [2] designed a model to predict specific energy consumption, which was validated in a turning process under conventional cutting speeds. The authors found that specific energy consumption increases with increasing cutting speed. In [22], a model to predict power consumption was developed using the Response Surface Methodology (RSM), Support Vector Regression (SVR), and Artificial Neural Networks (ANNs), while the RSM and genetic algorithms were employed to design optimization models during turning using only conventional cutting speeds. According to the results of this study, power consumption increases with the increase in cutting parameters.
Paul et al. [23] investigated the influence of depth of cut, feed rate, and tool geometry on specific cutting energy and back force during turning at conventional cutting speeds. Singh and Kant [24] introduced an integrated model to predict energy consumption and the corresponding machining parameters using a conventional cutting speed. Moreover, Xie et al. [25] presented a multi-objective optimization model based on surface roughness and energy saving for the selection of the optimum cutting parameters during the turning of a cutting insert at conventional cutting speeds. Abbas et al. [26] employed optimization models to select the optimal cutting conditions during the turning of AISI 1045 steel using uncoated tungsten carbide inserts and considering parameters such as surface roughness, power consumption, and total machining cost. The authors only used a conventional cutting speed.
Makhfi et al. [27] developed an ANN model to predict the influence of cutting parameters on cutting force components using a dataset on hard turning of AISI 52100 steel. The authors first optimized the number of hidden layers and the type of transfer functions in hidden and output layers and compared some algorithms, which were used in the final ANN model.
Karabulut [28] employed ANNs and regression analysis to predict surface roughness and cutting force during the milling of metal-matrix composites. According to the results, the ANN method was able to predict such variables with a low mean squared error.
Dahbi et al. [29] used an ANN approach to model surface roughness, cutting forces, cutting temperature, Material Removal Rate (MRR), cutting power, and specific cutting pressure during the turning of an aluminum alloy under different turning parameters. In addition, the authors selected the best architecture of the network.
Hanief et al. [30] developed a model to investigate the effects of cutting parameters on cutting forces during the turning of red brass using a high-speed steel cutting tool.
In addition, these authors demonstrated that the ANN model was able to predict the cutting forces more accurately than the regression one and that cutting force was largely influenced by feed rate.
Arnold et al. [31] applied a machine learning method with ANNs to determine the specific cutting force in a milling operation. Zerti et al. [32] studied the influence of machining parameters on surface roughness, cutting force, and cutting power during the hard turning of AISI 420 steel. According to the results of the ANOVA for main cutting force, depth of cut was found to have the greatest influence. Additionally, the ANN models proved to be more accurate than the RSM models.
Peng et al. [33] presented a supervised machine learning model to predict specific cutting forces, which was applied in a broaching operation. The results showed that this method provided a more accurate prediction than the linear regression model. For their part, Wenkler et al. [34] designed an ANN method to predict the specific cutting force in a milling operation. Hashemitaheri et al. [35] introduced a support vector regression model and a Gaussian process regression model to predict specific cutting forces and maximum tool temperatures in orthogonal machining. The data were generated using the finite element method.
Curra et al. [36] developed a model to predict specific energy consumption using an ANN during the turning of an AISI 316L steel and compared dry machining with the minimum quantity of lubricants. The authors used a JX1 ceramic as the cutting tool and up to intermediate cutting speeds.
According to this literature review, there are few studies into the turning of carbon steel dealing with the optimal selection of cutting parameters based on cutting forces and energy consumption.
Thus, the purpose of this study is to investigate the effects of cutting tool materials and cutting speed on cutting forces and Specific Energy Consumption (SEC) during the dry high-speed turning of AISI 1045 steel. The cutting forces are experimentally measured and compared with the results of a supervised learning algorithm. The effectiveness of the proposed model is validated based on the accuracy in terms of functional fitting using two performance metrics (mean squared error and the coefficient of determination). The model selected for each insert allowed us to obtain the values of the SEC in each of the established cutting regimes.
2. MATERIALS AND METHODS
2.1 Workpiece material
In this study, AISI-SAE 1045 steel was selected as the workpiece material. Its characteristics are presented in [37].
2.2 Characteristics of inserts
Coated carbide GC4225-P25 and uncoated cermet CT5015-P10 inserts were used during the experiment to calculate cutting forces. Cutting tools were manufactured by Sandvik and their characteristics are specified in [37].
2.3 Machine tool
The workpieces were machined on a MILLTRONICS CNC lathe machine with a maximum spindle speed of 3000 r/min and a spindle power of 9/7.5 kW. The samples had a diameter of 80 mm and a length of 300 mm. The length/diameter ratio was kept lesser than 10 to avoid chatter during machining. The workpieces were mounted between the chuck and the tailstock.
2.4 Formulation
In this study, the dependence between cutting forces and cutting parameters is determined by means of a neural network that represents the functional relationship between them. The following relationships are used to calculate the rotational speed (1) and the test duration (2):
where
n: rotational speed (r/min);
vc: cutting speed (m/min);
D: workpiece diameter (mm).
where
T: test duration (min);
L: workpiece machining length (mm);
f: feed (mm/r).
Since the power consumption of machine tools is dominated by the power consumption of the spindle system, this article will focus on the latter [2].
SEC is the energy consumed by the spindle system when machining 1 cm3 of material. As a result, the model can be expressed as (3) [2]:
Here, Ec represents the energy consumption of the spindle system during the machining process (4); V, the volume of material removal (5); Pi(t), the input power of the spindle system at t (6); MRR(t), the material removal rate at t (7); Pc(t), the cutting power of the machining operation (8); Pu(N), the idle power (9); Pad(t), the additional load loss of the spindle system (10); asp, the depth of cut; and T, the test duration. Functions Pc(t), Pu(N), and Pad(t) are, respectively, given by [2].
Finally, Fr(t) is the resultant cutting force (11); and Fx(t), Fy(t), and Fz(t), the components of the cutting force over time, which will be predicted by the designed model using a supervised learning algorithm.
3. EXPERIMENTAL DESIGN AND SETUP
3.1 Experimental data and software
This study measures the cutting forces of the coated carbide GC4225-P25 and uncoated cermet CT5015-P10 inserts during the dry high-speed turning of AISI 1045 steel at different cutting speeds and machining times.
The cutting depth (asp = 0.5 mm) and the feed (f = 0.1 mm/r) were kept constant during all tests. The experiment was conducted using two cutting tool materials (CT5015-P10 and GC4225-P25), three cutting speeds (vc = 400 m/min, vc = 500 m/min, vc = 600 m/min), and five test durations (T1, T2, T3, T4, and T5). A full factorial design with two replications was implemented to obtain the data [38].
The cutting forces were measured using a piezoelectric dynamometer (manufactured by Kistler) with a data acquisition card PC16024. National Instruments LabVIEW software was employed to analyze the data. Through an interface board, the analog signals obtained with the dynamometer were converted into digital signals.
The software used for data processing was MATLAB 2017b [39], as it offers the possibility to implement specific algorithms and carry out complex designed operations.
From the experimental test during the turning of AISI 1045 steel, data on cutting speed (vc), test duration (T), machining (observation) time (t), number of passes (np), and position of the cutting tool on the workpiece (pc) were recorded for each insert. These data were entered into MATLAB as vectors consisting of five independent variables (vc, T, t, np, and pc) and three dependent variables that denote the cutting forces (Fx, Fy, and Fz).
Table 1 shows the experimental design matrix used in this study and from which the cutting forces were measured.
3.2 Cutting force patterns
Measuring cutting forces in machining operations makes it possible to identify behavior patterns across the different stages of the process (i.e., start, cutting, return, cutting, return, cutting, and so on) until the test duration is completed. Figure 1 shows the cutting force values per record.
Given the need to predict behavior patterns in machining operations, tools that can extract complex linear and non-linear relationships from a data set, without prior knowledge of the phenomenon being modeled, are required. In this regard, regression techniques have proven to be effective in index estimation given their potential for function fitting. In this study, multiple regression and ANN methods were used to model the relationships between cutting parameters and cutting forces.
3.3 Multiple linear regression analysis
Due to the regularities in the distribution of the shear force values, their complexity may prevent one from obtaining a predictive model through multiple regression. This is mainly due to the density of records in each cutting regime and the variability between measurements given uncontrolled process vibrations and other external effects.
However, different models were obtained considering polynomials whose degrees ranged from one to five. In all the cases, the estimation accuracy was found to be insufficient according to the standardized values in the field of study for the two performance metrics employed: coefficient of determination (R2) and Root Mean Squared Error (RMSE).
3.4 Neural network configuration
When considering several designs of Function Fitting Neural Networks (FFNN) (shown in Table 2), the best results in terms of their performance in the processing of the datasets of both inserts were obtained when similar topologies were used.
When designing the model, a manageable number of topologies were considered, and the rest were discarded because of poor performance. From each topology, the 10 best models obtained with the same initial conditions were identified. Finally, a FFNN topology consisting of an input layer with 5 neurons, an output layer with 3 neurons, and a hidden layer with 25 neurons (Figure 2). Here, Ii (1 ≤ i ≤ 5) denotes the neurons of the input layer; Hh (1 ≤ h ≤ 25), the neurons of the hidden layer, where bh represents its bias and wih are the weights of the connections between the input and hidden layers; and Oo (1 ≤ o ≤ 3), the neurons of the output layer, where Bo represents its bias and Who are the weights of the connections between the hidden and output layers.
The combination of the best results considered, as activation functions, the hyperbolic tangent sigmoid and the linear in the hidden and output layers, respectively, as well as the Levenberg-Marquardt backpropagation training algorithm.
The 16 357 records for the CT5015-P10 insert were distributed as follows: 60 % for training, 20 % for validation, and 20 % for testing, as such distribution provided the least error. Similarly, records were uniformly selected: for subsets of five consecutive records, three records, one record, and one record were randomly chosen for training, validation, and testing, respectively.
In the case of the 16 419 records for the GC4225-P25 insert, the distribution that turned out to be the best was 70 %, 15 %, and 15 %. For every 20 consecutive records, 14 records, 3 records, and 3 records were randomly chosen for training, validation, and testing, respectively.
4. RESULTS AND DISCUSSION
After conducting an extensive experimentation to obtain the predictive models, which exhibited the best performances in both supervised learning approaches, the superiority of the model developed with FFNN was confirmed. The complexity present in the relationship between the analyzed variables was not even 90 % described by the polynomial regression models. According to Table 3, such models are a poor fit to the experimental data and are also characterized by high RMSE values.
On the contrary, the FFNN models were found to better fit the behavior patterns of the cutting forces based on the parameters considered, since their support structure is designed to describe the complex variability in the variables under study, as is the case of this research.
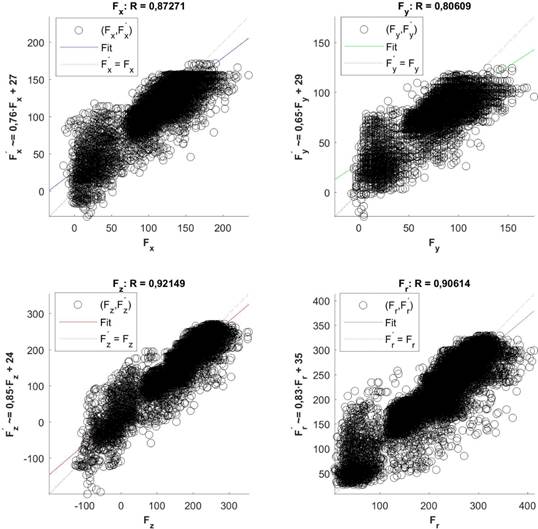
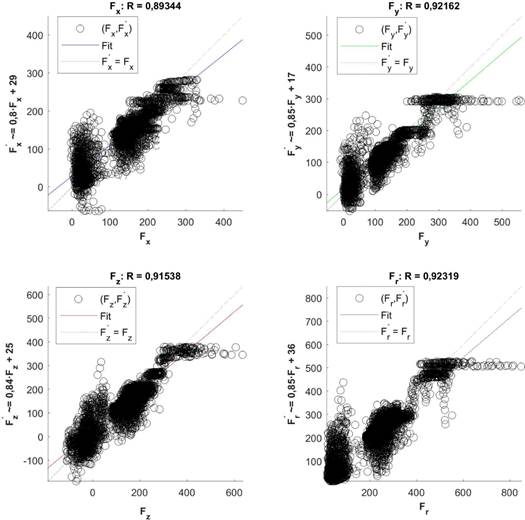
For the designed FFNN models, Figures 3 and 4 show the fitting level of the components of the estimated cutting forces (y-axis) to the components of the experimental cutting forces (x-axis). For each insert, the point cloud is over the equality line, which is confirmed by the fact that the value of the regression coefficient (R) is close to 1.
Source: Authors’ own work.
Figure 3 Regression of FFNN model representing the cutting forces for P10 insert
Source: Authors’ own work.
Figure 4 Regression of FFNN model representing the cutting forces for P25 insert
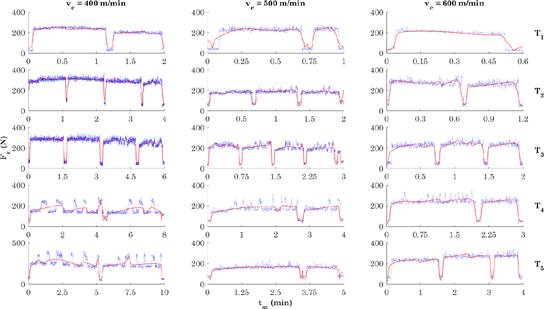
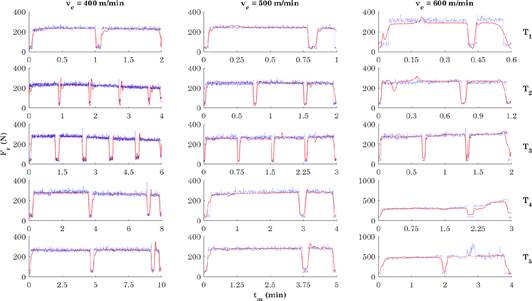
Figures 5 and 6 illustrate the accuracy of the efficiency indexes (i.e., error value or R-adjustment) based on the values of the resultant cutting force. The blue point cloud represents the experimental values; and the red line, the values estimated by the model in each cutting regime under analysis. The cutting speed levels and test duration levels are displayed in columns and rows, respectively.
Source: Authors’ own work.
Figure 5 Model fitting of the resultant cutting force per cutting regime for the CT5015-P10 insert
Source: Authors’ own work.
Figure 6 Model fitting of the resultant cutting force per cutting regime for the GC4225-P25 insert
The observed proximity between the resultant cutting forces led to the SEC values presented in Table 4. According to this table, there is a small difference between the mean values of the experimental and estimated SEC in all the experiment combinations. In addition, in most cases, the values of the deviations induced by the error are smaller for the estimated results. Therefore, the range of values for the estimated SEC constitutes a subset of the range of values for the experimental SEC.
Table 4 Experimental specific energy consumption vs. estimated specific energy consumption
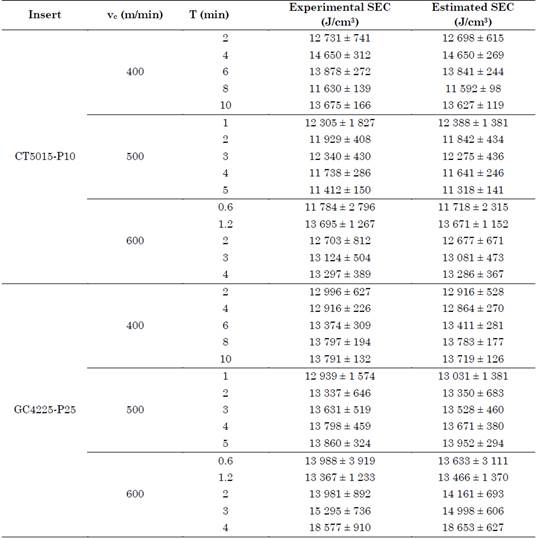
Source: Authors’ own work.
The highest SEC for the CT5015-P10 insert occurred at a cutting speed of 400 m/min with a test duration of 4 min; and for the GC4225-P25 insert, at a cutting speed of 600 m/min with a test duration of 4 min. The lowest SEC for the CT5015-P10 insert occurred at a cutting speed of 500 m/min with a test duration of 5 min; and for the GC4225-P25 insert, at a cutting % higher than that for the CT5015-P10 insert. These results show the complexity of the machining process, which depends on a considerable number of factors.
The coefficients of determination and the root mean squared error of the polynomial models did not exceed 80 % in the representation of the variability of the data. Those of the models developed with neural networks, however, exceeded 90 %, which represents an acceptable performance in the functional fitting of the shear forces. These findings reveal the good level of reliability of the FFNN models in predicting SEC under various machining conditions to further adopt the necessary energy-saving strategies.
These models could support engineers' decision-making by providing them with knowledge-based assistance. As auxiliary tools, they could be used to explore the behavior of different cutting regimes in terms of adopting resource-saving measures.
5. CONCLUSIONS
In this paper, the cutting forces, and the Specific Energy Consumption (SEC) during the dry high-speed turning of AISI 1045 steel were modeled using a function fitting neural network topology. For this purpose, we described the experiments and data sets derived from them, which formed the knowledge base learned by the model developed in MATLAB. The estimation of the SEC under the different cutting conditions proved to be highly accurate, which was corroborated by the values of the performance metrics and the graphical representations.
The cutting forces were experimentally measured and compared with the estimates of the predictive models developed using polynomial regression and artificial neural networks. The resulting models were evaluated based on two performance metrics (coefficient of determination and root mean squared error). The polynomial models were found not to exceed 80 % in the representation of the variability of the data, while the models developed with neural networks exceeded 90 %, which is an acceptable accuracy in terms of the functional fitting of the cutting forces. These results are consistent with those reported in [28], [30], [32], [33].
These findings show the good level of reliability of the FFNN models in predicting SEC under various machining conditions to further adopt the necessary energy-saving strategies.
The highest SEC for the CT5015-P10 insert occurred at a cutting speed of 400 m/min with a test duration of 4 min; and for the GC4225-P25 insert, at a cutting speed of 600 m/min with a test duration of 4 min. The lowest SEC for the CT5015 insert occurred at a cutting speed of 500 m/min with a test duration of 5 min; for the GC4225 insert, at a cutting speed of 400 m/min with a test duration of 4 min. Likewise, the intermediate cutting speed (vc = 500 m/min) produced the lowest SEC values for both inserts. Moreover, the SEC for the GC4225 insert was 8.943 % higher than that for the CT5015 insert.
These results confirm the complexity of the machining process, which depends on a considerable number of factors. Therefore, further work needs to be done with a higher number of replicates and a greater range of cutting speeds, as well as with other cutting tool materials.































