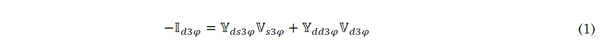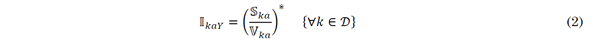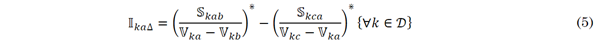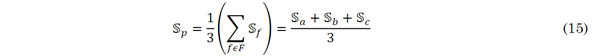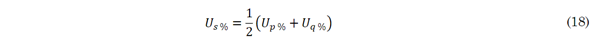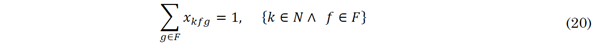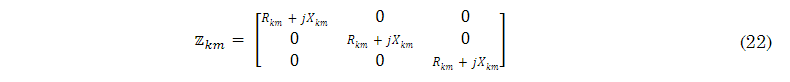1. INTRODUCTION

Electrical distribution networks are the most extensive systems in any country’s general electrical grid ^[1]. These systems are responsible for providing electricity to all energy users in medium- and low-voltage level applications while ensuring reliability, continuity, security, and efficiency ^{[2], [3]}. The general structure of electrical distribution networks has three phases, i.e., three conductors - phases a, b, and c - are used to efficiently distribute energy. Under balanced operating conditions, these networks are very efficient, as they ensure the lowest possible energy losses ^{[4], [5]}. Nevertheless, the real nature of electrical networks is unbalanced, given that (i) the distribution transformers that interface energy users and the grid have single-, two-, and three-phase connections ^{[6], [7];} (ii) due to the length of the feeders, grid construction does not apply the concept of transposition, which is typically used in transmission networks ^[8]; and (iii) the electrical behavior of each node’s users is not balanced, which implies that different current levels are requested per phase ^[9].

The above can cause unbalanced distribution networks to experience higher levels of energy losses and deteriorated voltage profiles in comparison with their balanced equivalents^[10].

To efficiently deal with the issue of unbalanced operation in three-phase asymmetric distribution networks, the specialized literature has proposed multiple strategies, some of which are currently known as phase-balancing or load redistribution problems. Some of the classical and recent solution methodologies for this problem are presented below.

The authors of ^[10] developed a mixed-integer convex model to minimize power losses in three-phase distribution networks, using a quadratic formulation. This optimization model is based on the concept of electrical momentum, which allows the resistive effect of all distribution branches to be included in the value of the expected objective function. Numerical results in the 8-, 15-, and 25-bus grids demonstrated the effectiveness of the proposed optimization model when compared to heuristic algorithms such as a genetic algorithm (GA) or the vortex search algorithm (VSA).

In ^[11] an optimization model based on the general active power imbalance, using a real variable domain representation of redistributed unbalanced loads in three-phase networks is presented. The general mixed-integer convex structure of this model ensures solution repeatability. Numerical results in the 8-, 15-, and 25-bus feeders demonstrated the effectiveness of this proposal in comparison with metaheuristic optimizers such as the sine-cosine algorithm (SCA) and the black hole optimizer (BHO).

The study by ^[8] proposed a specialized GA to reduce active power losses in three-phase asymmetric distribution networks. The main advantage of this approach is that it incorporates single-, two-, and three-phase loads connected to the grid. Numerical results in a 19- and a 37-node grid demonstrated this proposal’s ability to provide a set of feasible solutions to reduce power losses, thus providing more alternatives for the physical implementation of phase-balancing plans.

In ^[12], the VSA was implemented with a discrete codification to minimize the active power losses of a three-phase unbalanced distribution network. A master-slave solution methodology involving the combination of the VSA and the three-phase power flow method based on the iterative backward/forward approach yielded effective results in 8-, 25-, and 37-bus grids when compared to a GA. In addition, the results obtained with the VSA were improved by applying the discrete version of the crow search algorithm.

Additional works on optimal phase-balancing in three-phase distribution networks employ particle swarm optimization (PSO) ^{[9], [13]}, the heuristic algorithm based on pole measurement ^{[7], [14]}, and GAs based on group theory ^[6], among others.

Considering the above, the contributions of this research are presented below.

It should be noted that the main goal of this research is to minimize the expected grid power losses via load redistribution at all nodes, which also allows for the improvement of voltage profiles in each phase of the distribution network. In addition, within the scope of our work, it is considered that (i) peak-load data have been provided by the distribution company and all users have the same energy consumption profile, i.e., the electrical grid feeds only one type of user (residential, commercial, or industrial); (ii) the electrical infrastructure is three-phase and the impedance couplings between each pair of phases are negligible; and (iii) all the loads can be independently rotated in positive and negative sequences, i.e., the system does not contain any electrical machines that are directly connected to the grid or all of them are integrated via speed variators.

For the three-phase power flow implementation via the successive approximation’s method, it is assumed that all the loads are solidly grounded and have a star connection. In addition, the system is three-phase and three-wire, i.e., no neutral cables have been installed^[12].

The remainder of this research document is structured as follows. Section II presents the general power flow formulation for electrical networks, which uses the nodal admittance representation, an essential tool for determining the initial and final power losses of the grid as a function of the load connection. Section III describes the proposed mixed-integer convex formulation for the efficient redistribution of the nodal load connections while considering three objective functions. Section IV shows the general implementation of the solution methodology and its integration with the successive approximations power flow formulation. Section V describes the main characteristics of the three-phase version of the 35-bus network, which was used as a test system. Section VI shows all the computational validations carried out, and, finally, Section VII provides the main concluding remarks of this research.

2. METHODOLOGY

This section presents the proposed solution methodology to reduce power losses and improve voltage profiles in three-phase unbalanced distribution networks. Firstly, the three-phase power flow problem is formulated and solved via the successive approximation’s method. Secondly, the mixed integer convex programming model (MICP) is formulated, which includes three different objective functions.

2.1 The three-phase power flow problem

Under steady-state conditions, an electrical distribution network with a single- or three-phase representation can be expressed via a set of nonlinear non-convex equations regarding the apparent power equilibrium per node (i.e., the combination of Kirchhoff’s laws and Tellegen’s second theorem) ^[15]. This representation is possible since it is assumed that the electrical grid is fed using balanced voltage profiles following a sinusoidal behavior with constant amplitude and frequency at the terminals of the substation. The general power flow problem in three-phase networks can be formulated using (1).

Here, I _d3φ ∈ C ^{3 (n-1) × 1} is the vector of the demanded currents, defined in the complex domain for a network of n nodes where the substation’s injected current is removed; V _d3φ ∈C ^{3 (n-1) × 1} denotes the vector of complex voltages in all the demand nodes, which are the unknown variables of interest; V_s3φ ∈ C ^{3 × 1} is a complex vector that defines the voltage output at the substation terminals, i.e., a perfectly known vector; Y_ds3φ C ^{3 (n-1) × 3} is a submatrix stemming from the nodal admittance matrix that associates the substation bus with the remaining demand nodes; and Y _dd3φ ∈ C ^{3 (n-1) ×3 (n-1)} is a square matrix defined in the complex domain that is always invertible when the system is radially connected ( i.e., there are no isolated nodes). Note that the symbol C is used to represent the set of complex numbers.

Equation (1) looks like a set of linear equations due to its structure. However, note that the demanded currents are hyperbolic functions of the voltage profiles and constant power consumptions of the nodes, along with their connection type (i.e., Wye or Triangle) ^[12].

To illustrate the possible load connections of a particular node k node in a three-phase network, consider the Wye and Triangle connections presented in Figures 1 and Figure 2.

Source: authors.

Figure 1 Schematic connection of a wye load on bus k 

Source: Authors.

Figure 2 Schematic connection of a triangle load on bus k 

In Figure 1, the common point to which all the loads are connected is assumed to be solidly grounded, i.e., without a differential potential with respect to the neutral point at the terminals of the substation (this implies that). V_no = 0 Thus, each phase current can be calculated as defined from (2) to (4).

Where I _kaY , I _kbY , and I _kcY represent the net current absorption for a Wye load connected at bus k; V _ka , V _kb , and V _kc represent the complex line-to-ground voltage variables associated with node k; S _ka , S _kb , and S _kc denote the complex power consumption per phase at bus k; and D is defined as the set containing all the load nodes.

According to Figure 2, the calculation of each current is the sum of two components, as each phase has two loads connected to it. Equations (5)-(7) present the current flows of the triangle loads.

Where I _ka∆ , I _ka∆ , I _kb∆ and I _kc∆ represent the net current absorption for a triangle load connected at bus k; and S _kab , S _kbc , and S _kca , denote the complex power consumption between each pair of phases on bus k.

Considering the definitions of the Wye and Triangle current consumptions per node, it is convenient to obtain a general formula to calculate each three-phase current at node k. Thus, the Wye currents in (2)-(4) can be compacted using (8).

Where V^⋇ _k3φ = [V^⋇ _ka V^⋇ _kb V^⋇ _kc]^T and S^⋇ _k3φ = [S^⋇ _ka S^⋇ _kb S^⋇ _kc]^T =[S^⋇ _kab S^⋇ _kbc S ^⋇ _kca ] ^T . In addition, diag (v) is a matricial operation that transforms the vector v into a diagonal matrix.

The Triangle load connections defined in (5)-(7) can be generalized using (9).

Where

Finally, considering the possibility of having a node k. with loads in a Wye or a Triangle connection, the demanded current at this node can be generally calculated as defined in (10).

Now, by analyzing (1) and (10), it can be stated that a nonlinear relationship between voltage and current makes it necessary to apply an iterative solution method in order to find the numerical solution to the power flow problem in three-phase unbalanced networks. In this context, the iterative solution to this problem, which is defined in (1), requires the following formula:

Where t is the iteration counter, and each component of I ^t _d3φ is calculated using (10). Note that (11) is known in the literature as the successive approximation power flow method ^[12^]. The iterative process starts when, t = 0 setting each component of the vector V⁰ _d3φ as V⁰ _k3φ = Vs3φ, for k = 2,3,…,n with V _s3φ defined as follows:

Where V _nom represents the nominal operating voltage of the three-phase network under analysis. The iterative process with (11) is carried out until the convergence criterion is met. This criterion is defined in (13).

Where ε is the acceptable tolerance, typically set between 1×10^-6 and 1×10^-10. 1×10^-10

To evaluate the total power losses level of the distribution network, (14) is used.

Where V _3φ = [V _s3φ ; V _d3φ ] ^T represents the vector containing all the voltages of the network, including that of the substation.

The flow diagram in Figure 3 summarizes the general solution of the three-phase power flow problem in unbalanced distribution networks via the successive approximations power flow method.

Source: Authors.

Figure 3 General implementation of the power flow model in three-phase networks using the successive approximations method 

2.2 Optimal load redistribution modeling

In reducing the power losses of three-phase distribution networks, the nodal connection of each load type plays a fundamental role, as all the voltages in the demand nodes are a function of the demanded current in (9) and (10), which also defines the expected power losses level expressed in (15).

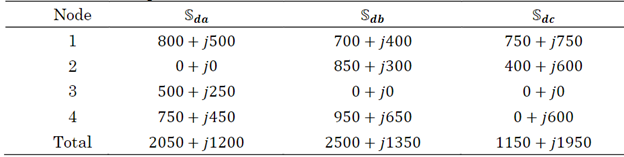
To formulate the efficient load redistribution model for the terminals of the substation, consider the following information for a 4-node grid (Table 1).

Table 1 4-node example for load redistribution at the substation terminals 

Source: Authors.

Regarding the total active and reactive power consumption per phase (Table 1), note that the total active and reactive power values are unbalanced, i.e., these values are different from each other. Therefore, the ideal active and reactive power consumption per phase can be defined as follows:

Which, for the example in Table 1, takes a value of S_p=1900+j1500. Here, F is the set containing all the phases, i.e., F ={a,b,c}

Regarding S_p as the expected load value per phase, three possible load redistribution scenarios can be analyzed, which are defined in (16)-(18).

Where, U _{p %} , U _{q %} , and U _{s %} denote the percent of active, reactive, or average apparent power losses at the substation terminals, which should ideally be zero, as is the case for three-phase balanced networks. The main characteristic of these objective functions is that all of them are convex, implying that an optimal value can be found if and only if all the constraints are convex or mixed-integer convex.

In three-phase networks, the phase-balancing problem implies that only a few load movements per node are admissible. Table 2 presents the load connection possibilities per node.

Each of the six possible load connections in Table 2 can be represented (19)-(20) with a binary matrix per node x _kfg , where the subscript k means the nodal connection, f represents the initial load connection, and g denotes the final load connection. In addition, as observed in Table 2, this binary variable only admits one position filled by one in each row and column, which yields the following set of linear-integer constraints.

Table 2 Load connection possibilities per node 

Source: Adapted from ^[11].

Where N represents the set containing all the nodes of the network. In addition, according to Equations (16)-(18), the total apparent power demand per phase at the terminals of the substation (i.e.,) S _f can be defined using (21).

Where S _kf represents the initial load connection at each node. The optimization model defined from (16) to (21) has a convex structure of mixed integers, which implies that an optimal solution can be reached using the branch and bound method combined with the modified simplex optimization algorithm ^[16].

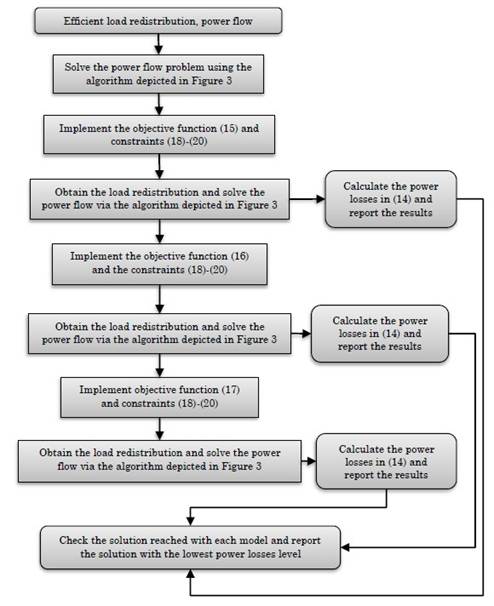
Figure 4 illustrates the general implementation of the proposed load redistribution model and its connection with the power flow problem presented in Figure 3.

Source: Authors.

Figure 4 General implementation of optimal load redistribution at the substation terminals in order to minimize grid power losses 

3. RESULTS AND DISCUSSION

This section describes the main numerical results obtained and discusses the application of the load balancing methodology to three-phase asymmetric networks, which combines a MICP approach with an efficient power flow solution. The first part of this section describes the main characteristics of the 35-bus system, and the final part focuses on the numerical validations, analyses, and discussions.

3.1 Three-phase 35 bus system

To demonstrate the applicability of the proposed methodology to reduce power losses in unbalanced three-phase distribution networks, which employ a hybrid optimization approach based on the power flow formulation and the mixed integer convex model (15)-(20), the three-phase equivalent of a single-phase 35-bus network is used. Figure 5 presents the nodal interconnections of this grid.

Source: Authors.

Figure 5 Nodal connections of the 35-bus system 

Note that this is a three-phase network that works with a line-to-neutral voltage of 15 kV at the terminals of the substation. In addition, Table 3 presents the per-phase parametric data of the 35-bus grid.

Table 3 Per-phase parametric information of the three-phase 35-bus system 

Source: Authors.

The information presented above (22) shows that, for a particular distribution line, the three-phase impedance matrix takes the following structure:

Table 4 presents the per-phase complex power consumption of the 35-bus system.

Table 4 Load information for each phase in the 35-bus grid 

Source: Authors.

3.2 Numerical validations

For the computational implementation or our proposal, the Julia programming environment (version 1.9.2) ^[17] was employed. The simulations were carried out on a 64-bit version of Microsoft Windows 10 Single Language, on a computer with an AMD Ryzen 7 3700 2.3 GHz processor and 16.0 GB RAM. The solution to the MICP model was obtained by means of the JuMP optimization environment and the HiGHS solver ^{[16], [18]}.

3.2.1 Benchmark case

To determine the effectiveness of the proposed complex-domain MICPmodel in reducing the power losses of the 35-bus system, the objective functions defined from (15) to (17) were evaluated. This, in order to determine the active, reactive, and apparent power imbalances of the reference case, i.e., the information presented in Table 4. The following results were obtained (note that 𝕊𝑝=3409.3333+𝑗1789.6667kVA):

• The total active power imbalance (i.e., 𝑈𝑝%), as defined by (15), was about 20.0561%.

• The total reactive power imbalance (i.e., 𝑈𝑞%), as defined by (16), was about 15.6630%.

• The total apparent power imbalance (i.e., 𝑈𝑠%), as defined by (17), was about 17.8445%

In addition, the initial power losses were calculated using (14) after solving the power flow problem via the successive approximations method described in Figure 3. The power losses for this system were 𝕊𝑙𝑜𝑠𝑠=473.1181+𝑗337.3563kVA. However, in electrical engineering applications, active power losses constitute the main interest, i.e., the real part of 𝕊𝑙𝑜𝑠𝑠(𝑃𝑙𝑜𝑠𝑠=Re{𝕊𝑙𝑜𝑠𝑠}=473.1181kW).

3.2.2 Results after solving the proposed MICP model

To reduce power losses in the studied three-phase 35-bus grid, the optimization model defined from (15) to (20) was solved while considering a single-objective analysis, i.e., each objective function (15)-(17) was optimized independently. Table 5 reports the general percent of active, reactive, and average apparent power imbalances before and after solving the optimization model for each of the performance indicators.

Table 5 Numerical results before and after optimizing the load connections 

Source: Authors.

The numerical results in Table 5 show that:

• All the objective functions can be minimized to values between 0.0245 and 0.0265%, which means that the proposed optimization model (15)-(20) is efficient.

• In all cases, minimizing the indices 𝑈𝑝%, 𝑈𝑞%, and 𝑈𝑠%allows for reducing the expected power losses value with respect to the initial case. The power losses are reduced by about 4.7045%when the active power imbalance is minimized. This reduction is about 5.8856%for the reactive power imbalance and 6.8652%for the average apparent power imbalance.

It is worth mentioning that, for this system, the best result regarding active power losses minimization (Table 5) was obtained by reducing the average apparent power imbalance. Nevertheless, this result cannot be generalized to any three-phase unbalanced distribution network due to the nonlinear relation between power losses and voltage profiles, in addition to the fact that the optimization model (15)-(20) is a mixed-integer linear approximation of the optimal load-balancing problem, and it assumes that there are ideal voltages and that all the loads can be moved to the substation terminals. In other words, each objective function must be evaluated to select the alternative that allows for higher reductions in total power losses in a given grid.

3.2.3 Voltage profile behavior

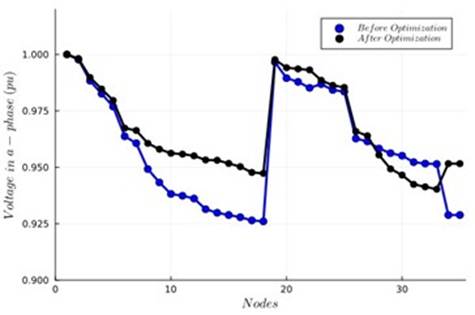
To demonstrate the positive effect of power losses minimization on the electrical performance of the studied three-phase distribution network with respect to power savings, the behavior of the per-phase voltage profile is shown depicted in Figures 6-Figure 8).

Source: Authors.

Figure 6 Per-node voltage profile behavior in the a-phase before and after implementing the load redistribution optimization approach 

Source: Authors.

Figure 7 Behavior of the voltage profile per node in the b-phase before and after implementing the load redistribution optimization approach 

Source: Authors.

Figure 8 Per-node voltage profile behavior in the c-phase before and after implementing the load redistribution optimization approach 

The main results observed in these figures are the following:

• The voltage profile behaviors for phases 𝑎 and 𝑏 show that minimizing the total grid power losses allows improving the voltage magnitude of most nodes (Figures 6 and Figure 7), whereas the voltage profile of phase 𝑐deteriorated with respect to the benchmark case (Figure 8). However, this is an expected result, as phases 𝑎and 𝑏were initially overloaded when compared to phase 𝑐 (Table 3), which implies that, after load redistribution, part of the loads present in phases 𝑎and 𝑏were transferred to phase𝑐.

• The overall voltage regulation of the 35-bus grid improved after load redistribution using the proposed optimization model. Note that the worst voltage magnitude occurred in phase 𝑏 for the benchmark case, with a magnitude of 0.8895 pu at node18, which defines an overall general regulation value of about 11.05%. Nevertheless, after implementing the optimization procedure, the worst voltage profile occurred at node 18 in phase 𝑏with a value of 0.9150 pu, i.e., the voltage regulation was about 8.95%in this context. This is a significant result, as regulatory policies for distribution companies typically impose a voltage regulation value of about 10%in medium-voltage applications. This criterion is met in this research.

3.2.4 Comparative analysis

To demonstrate the effectiveness of the optimization model defined from (15) to (20) with respect to the reduction of expected power losses in an unbalanced distribution network by minimizing the total equivalent load imbalance at the substation terminals, the IEEE 25-grid reported by ^[10] and ^[11] was considered. Table 6 reports the general percent active, reactive, and average apparent power imbalances before and after solving the optimization model for each one of the performance indicators.

Table 6 Numerical results before and after optimizing the load connections 

Source: Authors.

The numerical results in Table 6 show that:

• All the objective functions can be minimized to values between 0 and 0.0088%, which means that the proposed optimization model is efficient regarding the improvement of the power imbalances at the terminals of the substation.

• In all cases, minimizing the indices 𝑈𝑝%, 𝑈𝑞%, and 𝑈𝑠%allowsforreducing the expected power losses value with respect to the initial case. The power losses are reduced by about 3.7698% when the active power imbalance is minimized. This reduction is about 3.4997% for the reactive power imbalance and 3.8056% for the average apparent power imbalance. These results confirm that, forIEEE 25-bus grid, the most effective approach involves minimization ofaverage apparent power imbalance, as defined in (17).

• The proposed approach reports a final value of about 72.5505 kW regarding the expected grid power losses when the average power imbalance is minimized. In contrast, the mixed-integer quadratic convex presented by ^[11] reports a final value of about 72.2816kW, which implies a difference of about 0.2689 kW (0.3565%) between both methodologies. These results confirm that our complex-domain proposal provides an adequate approximation of the solution reported with the MIQC approach in ^[11], with the main advantage that the proposed MICP model is simpler, since it does not requireinformation aboutthe branches in the optimization stage.

• A comparative analysis with metaheuristic optimizers was performed, which included PSO, Chu & Beasley GA, and BHO. When the optimization model (15)-(20) is solved with these methods and their solution is evaluated via the successive approximations power flow approach in order to determine the final power losses values, the standard deviations are different from zero, i.e., the mean value differs from the minimum value after multiple executions (these variations were between 0.50 and 1.75%), implyingthat the metaheuristic optimizers cannot converge to the same numerical solution, which is always ensured with the proposed MICP approach.

4. CONCLUSIONS

This research presented a new optimization methodology based on a mixed-integer convex formulation in the complex domain to redistribute the constant power load consumption of three-phase unbalanced distribution networks, with the aim of minimizing the grid power imbalances at the terminals of the substation, reducing the expected grid power losses, and improving the voltage profile performance at each phase of the system. This solution methodology is based on two stages. The first stage solves the proposed MICP model while separately considering three objective functions, i.e., the active, reactive, and average apparent power imbalances. The second stage solves the three-phase power flow problem in order to identify which objective function yields lower power losses compared to the benchmark case.

Numerical results in the 35-bus grid show that power losses can be reduced by 4.7045-6.8652 % using the proposed methodology, depending on the objective function analyzed.

The most important result of this research has to do with the combination of a MICP formulation in the complex domain (as a relaxation of the optimal phase-balancing problem in three-phase distribution grids) and an efficient power flow method based on successive approximations, with the aim of reducing the power losses of unbalanced distribution networks after implementing the load connection plans provided by the solution of the MICP model. Note that the solutions found are optimal for each objective function under analysis, since the objective function is convex and the solution space is mixed-integer convex, which implies that combining the branch and cut method with an interior-point optimizer is possible and can ensure a globally optimum.

It is essential to note that the proposed approach requires evaluating all objective functions (i.e., the active, reactive, and apparent power imbalances) in order to determine the best alternative for reducing the total power losses of a specific three-phase grid. This is an important element of our proposal; due to the MICP method’s relaxation of the power balance constraints by the MICP method, the solution obtained is optimal, but it can correspond to an approximate solution in the case of the full power flow model.

A possible limitation of our contribution is that it neglects the effect of the distribution branch impedances on the calculation of power losses, since the MICP approach only focuses on balancing loads at the terminals of the substation. However, when the power flow problem is solved with the successive approximation’s method, the final power losses are adequate with regard to the expected reduction values, even though they correspond to an approximation of the exact optimization model.

As future work, (i) different objective function structures could be evaluated in the three-phase grid model, such as quadratic functions and norms, in combination with convex approximation; and (ii) metaheuristic optimization techniques could be applied to define the best load combination per node in order to minimize power losses via a master-slave optimization methodology. In this methodology, a metaheuristic approach could be assigned to define the load connection per node in the master stage, and the successive approximations power flow method could be used in the slave stage to guide the exploration and exploitation stages.