INTRODUCCIÓN
Los primeros estudios e investigaciones sobre modelación numérica de vertederos fueron desarrollados en 1965 por Cassidy, quien con un modelo numérico en dos dimensiones utilizó la suposición de flujo potencial para establecer la presión sobre la cresta de aliviadero. Se desarrollaron modelos numéricos multifásicos para un vertedero con paso escalonado, donde se recurrió a un índice de convergencia de la red para reducir el error de discretización. Los resultados numéricos se verificaron mediante de la comparación con el modelo físico a gran escala (Daneshkhah y Vosoughifar, 2011; Kositgittiwong, Chinnarasri y Julien, 2013).
En el estudio denominado “Modelado físico y comparación de CFD: estudio de caso de central hidrocombinada en modo de válvula” (Duró et al., 2012), se implementaron dos modelos de turbulencia y dos escalas para identificar las capacidades y limitaciones de cada enfoque y determinar la selección de criterios para el modelado dinámica de fluidos computacional (CFD, por su sigla en inglés) para este tipo de estructura. En este sentido, describir matemáticamente el comportamiento hidráulico en estructuras de control, conlleva a ecuaciones diferenciales acopladas no lineales, las cuales en la mayoría de los problemas de ingeniería no poseen una solución analítica. No obstante, es posible obtener soluciones aproximadas a partir del análisis de volúmenes finitos. El método de volúmenes finitos (FVM, por su sigla en inglés) es una técnica numérica que transforma las ecuaciones diferenciales parciales que representan las leyes de conservación sobre volúmenes diferenciales, en ecuaciones algebraicas discretas sobre volúmenes finitos (o elementos o células) (Moukalled, Mangani y Darwish, 2016). Este método convierte un medio continuo con infinitas variables, en un medio discreto, con geometrías establecidas y condiciones de contorno determinadas. Surge, así, la CFD, encargada de modelar el comportamiento de los fluidos sometidos a diferentes variables propias del sistema, implementando algoritmos computacionales; estos intentan describir el comportamiento real del fluido bajo diferentes escenarios. El problema está gobernado por las ecuaciones de Navier-Stokes para flujo incompresible.
En este estudio, se caracterizó el comportamiento de la estructura de control y el sistema de compuertas El Quimbo a partir de la modelación numérica con el método de volúmenes finitos, para elevaciones del labio de la compuerta a 704 m s.n.m., 706,9 m s.n.m., 709,4 m s.n.m., 712 m s.n.m. y 724,6 m s.n.m. El sistema de control de El Quimbo está compuesto por cuatro vanos independientes de 14,25 m de ancho controlados por compuertas radiales de 14,25 m de ancho y 18,40 m de altura, tres pilas tipo III de 4,0 m de ancho dos estribos con radio de 6 m, y un azud tipo Ogee Crest con cresta en la cota 702 m s.n.m. El empalme entre el paramento de aguas arriba y la curva que caracteriza la curva del azud, se realiza por medio de un arco de elipse. La curva del azud empalma con el canal de descarga de pendiente mediante una curva vertical cóncava con radio de 56 m. El canal de descarga tiene un ancho constante de 69 m y entrega el flujo al lecho del río por medio de un deflector radial tipo salto de esquí con radio de 30 m, con punto de disparo en la cota 614,08 m s.n.m. y ángulo de lanzamiento de 35 grados. El modelo físico fue realizado por la Universidad Nacional de Colombia (sede Manizales), y el diseño de la estructura fue realizado por Ingetec. Finalmente, en este estudio se desarrolló el modelo numérico bidimensional con el método de volúmenes finitos basado en ecuaciones de continuidad, utilizando el software ANSYS Fluent 17.0.
METODOLOGÍA
Simulación numérica CFD
La modelación numérica de fenómenos hidrodinámicos conlleva a la resolución de las ecuaciones de Navier-Stokes gobernantes para fluidos. Es posible obtener una solución aproximada mediante la aplicación del método de volúmenes finitos. Así, los modelos CFD están gobernados por las ecuaciones (1), (2) y (3):
Continuidad,
Moméntum,
Presión,
Donde,  es la velocidad del flujo, ρ es la densidad del fluido,
es la velocidad del flujo, ρ es la densidad del fluido,  es la fuerza del cuerpo, p es la presión,
es la fuerza del cuerpo, p es la presión,  es la aceleración de la gravedad, µ es la viscosidad del fluido.
es la aceleración de la gravedad, µ es la viscosidad del fluido.
Descarga en vertederos tipo Ogee
En el caso de un vertedero tipo Ogee, la descarga con apertura total de compuertas se da por la ecuación (4):
Donde, Q es el caudal descargado (m3/s), C D es el coeficiente adimensional de descarga para vertederos hidráulicos, 𝑔 es la aceleración de la gravedad (m/s2), L es la longitud efectiva en la cresta (m), 𝐻 es la carga hidráulica total incluyendo la altura de velocidad (m).
La descarga de flujo bajo la compuerta radial es una función de los parámetros geométricos e hidráulicos, de la profundidad del agua aguas arriba, la profundidad del agua aguas abajo, la apertura de la compuerta, el radio de la compuerta y la altura del pasador del muñón (Zahedani, Keshavarzi, Javan y Shahrokhnia, 2012). Para aperturas parciales de compuertas, la descarga está gobernada por la ecuación (5):
La descarga de la compuerta se define como libre cuando el chorro de aguas abajo de la puerta está expuesto a la atmosfera y el labio de la compuerta no está sumergido. En tal sentido, el flujo inmediatamente aguas abajo de la compuerta es supercrítico y un resalto hidráulico se forma aguas abajo de la compuerta (James y Young, 2001). En consecuencia, el flujo sale desde el deflector como una descarga libre hacia arriba y cae de nuevo en el río aguas abajo del extremo del aliviadero. La trayectoria del chorro se asume dependiente de la energía de flujo disponible en el deflector y del ángulo de disparo. Así la trayectoria del chorro está dada por la ecuación (6) (United States Department of the Interior, Bureau of Reclamation, 1987).
Donde, θ es el ángulo del borde del labio con la horizontal (°), x es la distancia horizontal medida a partir del punto de disparo (m), h es la profundidad de la lámina de agua en el punto de disparo (m), hv es la altura de velocidad (m).
Modelo numérico bidimensional
Se desarrolló un modelo numérico bidimensional sin considerar el efecto de las pilas y los estribos en el azud, a escala 1:70, bajo condiciones de flujo permanente de la estructura de control y del sistema de compuertas radiales de la represa El Quimbo, a partir de la implementación el software ANSYS Fluent 17.0.
El análisis hidrodinámico de la estructura se realizó bajo condiciones de superficie libre, y con diferentes cargas hidráulicas y para las siguientes elevaciones del labio de las compuertas: 704 m s.n.m., 706,9 m s.n.m., 709,4 m s.n.m., 712 m s.n.m. y 724,6 m s.n.m. Se evaluó el comportamiento de los valores residuales hasta obtener el nivel de convergencia. Se estudió la independencia de la malla para determinar el nivel de refinamiento óptimo. Se analizaron las condiciones de contorno de entrada y de salida del flujo, el comportamiento de la lámina de agua a través del vertedero, los coeficientes de descarga, las velocidades de aproximación y las variaciones en los campos de presión desarrollados en el sistema de compuertas radiales, en la rápida y en el deflector. Luego, se validó el modelo numérico, a partir de la comparación de los resultados numéricos con los datos teóricos encontrados por Ingetec y los datos de las pruebas realizadas en el modelo físico desarrollado por la Universidad Nacional de Colombia (sede Manizales). Se evaluó la capacidad del modelo numérico para simular el comportamiento hidráulico del modelo físico, encontrado el grado de variación de los datos reales con los datos obtenidos mediante la simulación numérica.
Fases e independencia de la malla
El modelo numérico bidimensional se basó en un modelo multifase (VOF), estableciendo dos fases. Una fase es el agua, y la otra corresponde al aire, en condiciones de flujo libre (open channel flow). La carga hidráulica inicial se estableció en 1,6 m, la cual se modificó según el caso de estudio. Se optó por la generación de una malla estructurada multizona, realizando un especial refinamiento en cercanías al muro generando una compuerta móvil para diferentes elevaciones del labio de las compuertas, comenzando por la cota 704 m s.n.m., hasta la cota 724,6 m s.n.m. (CMP). Para estabilizar el flujo de entrada asociado a las condiciones reales del sistema se colocó un tanque de amortiguación antes de la gola con el objeto de disminuir las perturbaciones generadas por el ingreso del agua al sistema. Se realizaron 5 mallas estructuradas para las siguientes elevaciones: 704 m s.n.m., 706,9 m s.n.m., 709,4 m s.n.m., 712 m s.n.m. y 724,6 m s.n.m. Estas cumplen con los parámetros de calidad en términos de ortogonalidad, oblicuidad y relación de aspecto. Debido a la variación de la malla por las diferentes elevaciones del labio de la compuerta se realizaron 27 simulaciones. En el análisis de independencia de la malla, se realizaron cuatro mallas diferentes para cada apertura. Por ejemplo, para un caudal de 72,5 lps con elevación del labio de la compuerta: 709,4 m s.n.m., se realizó una malla gruesa (18.458 nodos), una mediana (62.458 nodos), una fina (105.456 nodos) y una malla refinada (129.572 nodos). Para los cuatro casos simulados se utilizaron las mismas condiciones físicas y las mismas condiciones para el asistente de configuración de ANSYS Fluent (tabla 1).
Condiciones de frontera
En este estudio la simulación numérica se realizó para una descarga máxima de 290 lps (CMP) y una descarga mínima de 17.587 lps. De igual forma, estos caudales se variaron para diferentes escenarios con diferentes aperturas de compuertas. Así, las condiciones de frontera, como la entrada de flujo aguas arriba y en la salida aguas abajo, el límite sólido y las condiciones de flujo a superficie libre se consideraron como se observa en la figura 1.
Métodos de solución
Los solver de ANSYS Fluent se basan en el método de volúmenes finitos donde el dominio se discretiza en un conjunto finito de volúmenes de control. No existe una definición precisa de flujo turbulento, pero este tiene una serie de rasgos característicos como la irregularidad presentando patrones caóticos que pueden parecer al azar, los cuales están gobernados por las ecuaciones de Navier-Stokes (Pope, 2015). Se adoptó para este estudio el modelo de turbulencia k-épsilon, este resuelve las ecuaciones Navier-Stokes promediadas en el tiempo, este modelo ha demostrado ser estable, numéricamente robusto y tiene una capacidad predictiva bien establecida (ANSYS, 2013). Se adapta a flujos que presentan gradientes de presión como lo son los flujos en vertederos a superficie libre. De hecho, se ha demostrado la eficiencia del modelo k-épsilon en vertederos para caracterizar el comportamiento de la turbulencia, comparándolo con modelos más complejos como el modelo LES (Dehdar-behbahani y Parsaie, 2016). De hecho, la energía cinética de las grandes escalas se transfiere a escalas más pequeñas a medida que estas interactúan. La energía cinética se transforma en energía interna (Lars, 2017).
Se mantuvo por defecto los valores de las constantes C mu =0,0845; C 1 =1,42, y C 2 =1,68. Para la solución numérica se estableció el algoritmo SIMPLE (semi-implicit method for pressure-linked equations) en ANSYS Fluent (tabla 2), mediante factores implícitos de relajación. Se estableció 1,0 como número máximo de Courant para todas las modelaciones realizadas que corresponde al límite de convergencia de muchos esquemas numéricos explícitos. El criterio de convergencia para los residuos de turbulencia, presión y velocidad se tomó como 1e-5, y para la continuidad se estableció 1e-4. Estos residuos fueron monitoreados en el dominio para garantizar la estabilidad tanto en el embalse de entrada como en la estructura de control.
Las ecuaciones diferenciales parciales (conservación de masa, moméntum y energía) se discretizan en un sistema de ecuaciones algebraicas y se resuelven numéricamente para cada volumen de control. En la configuración del solver en ANSYS Fluent para este estudio se implementó el método variable para el tiempo con un número máximo de iteraciones por paso de 20 y un número de tiempos de paso de 20.000.
RESULTADOS Y DISCUSIÓN
Residuales
La condición de convergencia se alcanzó cuando la diferencia del caudal de entrada con respecto al caudal de salida fuera menor o igual al 0,8 %. Por ejemplo, para un caudal de 72,5 lps, con elevación del labio de la compuerta: 704 m s.n.m., bajo condiciones de flujo permanente. Así, se alcanzó convergencia después de 1,774.000 iteraciones, con una variación final de caudal del 0,2316 % (figura 2.).
Lámina de agua
Para un tiempo de retorno de 100 años, el modelo numérico estimó una lámina de 0,0306 m que corresponden a 2,143 m en la estructura El Quimbo, donde ingresaron al volumen de control 80.799 lps y salieron 80.732 lps, originado una variación en términos de caudal de 0,08316 %. Para un caudal de 103,95 lps y un tiempo de retorno de 1000 años, se midió en el modelo numérico una lámina de 0,0358 m equivalente a 2,769 m a escala (1:70), lo cual indica una variación de 0,0443 m con respecto a la obtenida por Ingetec y la Universidad Nacional de Colombia (sede Manizales), así mismo, la variación en términos de caudal fue de 0,0046 lps para la abscisa 2,635 m (figura 3.).
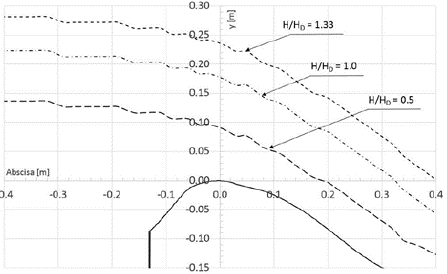
Fuente: elaboración propia.
Figura 3 Lámina de agua adimensional para diferentes cargas. Apertura: 724,6 m s.n.m.
El aumento de la relación H/HD conlleva al incremento del caudal descargado. Para la relación H/HD=1,0 sobre la gola la altura de la lámina es 0,175HD. Incrementando un 33 % la carga hidráulica en la entrada a la gola la lámina será de 0,24HD. En la figura 4 se observa la generación de perturbaciones en la entrada a la compuerta, originando pérdidas de energía como resultado de los cambios en la alineación de los límites (pérdida de forma) y en el desarrollo de la capa límite, según la USBR las pérdidas de forma en vertederos son despreciables.
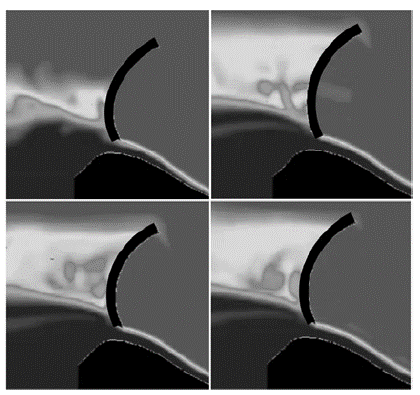
Fuente: elaboración propia.
Figura 4 Perfil de la napa en la gola. Elevación del labio de la compuerta: 704 m s.n.m.; caudal: 290 lps (CMP)
El flujo en el deflector para un caudal de 290 lps y una elevación de 704 m s.n.m., genera la aparición de remolinos turbulentos que disipan la energía para el ángulo de disparo de 35 grados, esto trae como consecuencia la disminución del alcance horizontal del chorro (figura 5).
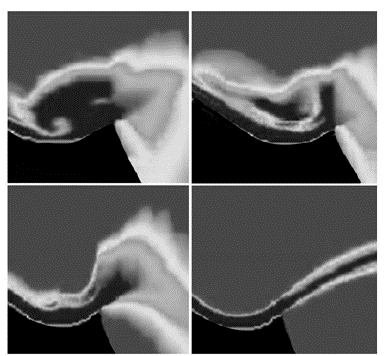
Fuente: elaboración propia.
Figura 5 Perfil de la napa en la gola. Elevación del labio de la compuerta: 704 m s.n.m.; caudal: 290 lps (CMP)
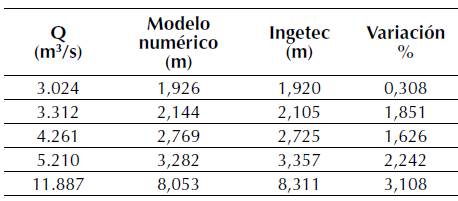
A continuación, se presenta la comparación de la lámina de agua obtenida en el modelo numérico con respecto a las alturas calculadas por Ingetec y la Universidad Nacional de Colombia (sede Manizales) (tabla 3):
Se observa que el aumento en la carga hidráulica en la entrada a la compuerta se incrementa la variación entre los datos experimentales y los datos del modelo numérico, llegando a una variación máxima del 3,108 % para la creciente máxima probable de 11.887 m3/s.
En términos adimensionales, para una apertura de compuertas de 704 m s.n.m. y una relación H/HD=1,0 y la CMP, el mayor alcance horizontal del chorro se origina en X=0,57HD.
Una vez la carga hidráulica aumenta con relación a la carga de diseño H/HD=1,33, el alcance horizontal del chorro aumenta y se desplaza a X=0,754HD. Para un caudal de 290 lps y para una elevación total de compuertas (724,6 m s.n.m.), la altura máxima que alcanza el chorro, para una relación de la carga hidráulica con respecto a la carga de diseño (H/HD=1,0), es de 1,20HD en X=0,55HD.
El alcance horizontal del chorro está determinado principalmente por la carga hidráulica, la apertura de la compuerta y el ángulo de disparo del deflector. Se obtuvo un alcance horizontal de 2,255 m para la creciente máxima probable con una elevación de compuertas de 704 m s.n.m.
Distribución de presiones
Cuando se aplica una carga hidrostática a la cara de la compuerta, la fuerza que actúa sobre esta pasa directamente a través del eje, y por tanto, el polipasto mecánico solamente levanta la masa de la compuerta, que puede ser equilibrada por la fuerza hidrostática efectiva (Chadwick y Morfett, 1989). En el modelo hidráulico para el deflector de 35° se tuvieron entonces presiones mayores, como era de esperarse, en el fondo de este, que alcanzaron valores máximos de 37,8 m.c.a. para la CMP (Mejía, Suárez y Vélez, 2012). Según los valores obtenidos por el modelo numérico, la relación H/HD=1,33 en términos de presión relativa sobre la gola en x=-0,17HD indica un valor crítico para la cavitación de hp=-0,18HD, lo que concuerda con lo indicado por la USBR, estableciendo que una carga hidráulica más alta que la del diseño, la trayectoria de la lámina de agua será más alta en la cresta, creando presiones negativas, resultando en el aumento de la descarga. Se evidencia que la presión relativa para H/HD=0,5 sobre la gola en x=0,092HD es cercana a cero (0) (figura 6). Según Ingetec (2013), existe la posibilidad de presentarse sobre el azud presiones negativas del orden de -7,62 metros columna de agua para la ocurrencia del caudal máximo de 11.886 m3/s.
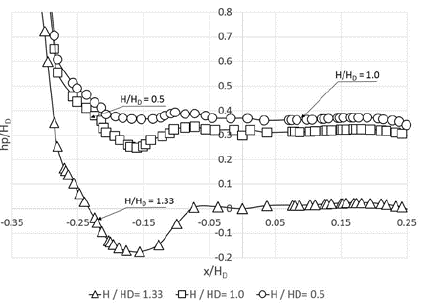
Fuente: elaboración propia.
Figura 6 Presión adimensional sobre la gola. Elevación del labio de la compuerta: 704 m s.n.m.
La presión en cualquier punto del canal puede ser medida mediante un tubo piezométrico, en el cual el agua ascenderá hasta el nivel de la superficie que presente el canal, es decir la presión corresponderá a la altura de la lámina de agua medida desde el fondo del canal hasta la superficie de esta (Chow, 1994).
Los resultados de las presiones obtenidos en el modelo numérico establecen la aparición de presiones subatmosféricas en la abscisa 2,737 m y en la abscisa 2.971 m de 250 Pa y 198 Pa respectivamente, para una elevación de 709,4 m s.n.m. y caudal de 290 lps, correspondiente la creciente máxima probable.
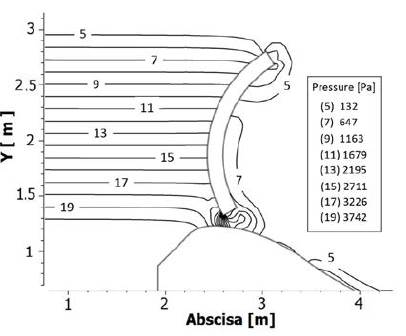
Fuente: elaboración propia.
Figura 7 Distribución de presión en la gola. Elevación del labio de la compuerta: 704 m s.n.m.; caudal: 72,5 lps
Estas presiones se encuentran dentro del rango de presiones incipientes establecido por la USBR. De igual forma, la condición de cavitación encontrada en la rápida puede ser considerada cavitación incipiente. Es importante aclarar que, aunque no se introdujo la aireación en la simulación numérica, los valores negativos encontrados para la presión no pueden llegar a afectar la superficie del vertedero.
Se evidencian oscilaciones de la presión dinámica, principalmente en el deflector. De hecho, se presentan mayores valores de presión en el empalme de la rápida con el deflector cuando la apertura de la compuerta disminuye. Así, para la abscisa 4,62 m del modelo numérico, con un caudal de 72,5 lps y una elevación de compuerta de 704 m s.n.m., se origina una presión dinámica máxima de 10.039 Pa. No obstante, los valores mínimos de la presión dinámica se presentaron antes de la compuerta. Como ya se mencionó, el mayor valor de la presión dinámica se alcanzará en la abscisa 4,62 m del modelo numérico, debido principalmente al cambio en la dirección de las líneas de corriente generado por la curvatura del deflector, luego la presión desciende súbitamente hasta los 6.000 Pa en la abscisa 5,10 m. A la salida del labio, evidenciando la aparición de presiones subatmosféricas. En términos adimensionales la fluctuación de la presión dinámica a lo largo del vertedero permanecerá positiva siempre y cuando el nivel del embalse este por abajo del nivel de inundación (CMP).
A medida que la relación entre la carga hidráulica y la altura de diseño aumenta, la presión dinámica también lo hará. Por ejemplo, para la relación H/HD=1,33, la presión dinámica adimensional es igual a 0,24HD en la abscisa 0,1HD. No obstante, para la relación H/HD=0,5 la presión dinámica adimensional es igual a 0,37HD en la abscisa 0,25HD. Para H/HD=1,0 en X=0,05HD se evidencia un coeficiente de presión de Cp=0,4HD. Sí la carga hidráulica aumenta con H/HD=1,33, el valor del coeficiente de presión disminuye a 0,02HD (figura 8).
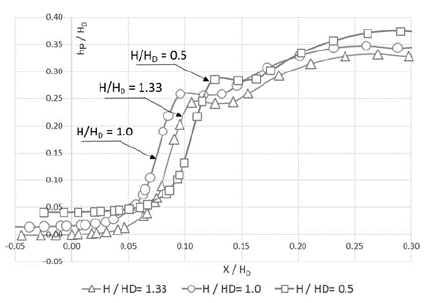
Figura 8 Presión dinámica adimensional en la gola (H/HD=1,33). Elevación del labio de la compuerta: 704 m s.n.m.
Velocidades de aproximación
Los resultados de la modelación indican una velocidad máxima de aproximación de 1.682 m/s, para la CMP y apertura del 100 % (724,6 m s.n.m.) (figura 10). Una vez el flujo supera el estado subcrítico en su paso por la gola a estado supercrítico en la rápida, se inicia el desarrollo completo del perfil de velocidades, experimentando una velocidad máxima en la rápida de 4,38 m/s para la abscisa 4,3 m y un caudal de 72,5 lps. De igual forma, se evidencia el comportamiento curvilíneo del perfil de velocidades de acuerdo con los principios teóricos que aplican para flujo en canales abiertos. De hecho, el diseño del deflector debe lograr un equilibrio entre el ángulo de disparo, el grado de disipación de energía, el alcance del chorro y la generación mínima de burbujas, las cuales inciden en la aparición del fenómeno de cavitación. En este caso y según los valores obtenidos para la velocidad, se encontró que en el deflector para la abscisa 5,1 m se origina una velocidad máxima de 5,18 m/s para un caudal de 72,5 lps y una elevación del labio de la compuerta de 704 m s.n.m. En esta abscisa se desarrolla de manera completa el perfil de velocidades.
Coeficiente de descarga
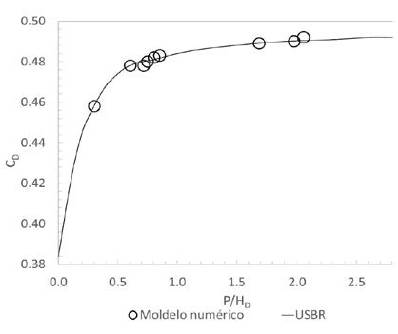
Para los coeficientes efectivos de descarga, el valor de C 0 se estimó mediante la metodología propuesta por la USBR (ecuación 4), con base en la profundidad del canal de aproximación (P) y de la altura de diseño HD. Mediante la carga máxima sobre la cresta correspondiente a 11,9847 m obtenida del modelo numérico, para la creciente máxima probable, se estimó un valor de C 0 de 2.019 y para C D de 0.454, por su parte Ingetec estableció para C 0 un valor de 2,047. El coeficiente de descarga C 0 depende de la profundidad de aproximación, de la forma real de la cresta y de la pendiente de la corriente. Asimismo, el parámetro HD se ve afectado por la altura de velocidad que experimenta el flujo en el paso por la gola, esta velocidad de aproximación es pequeña originado la máxima contracción vertical de la lámina (United States Department of the Interior, Bureau of Reclamation, 1987).
Fuente: elaboración propia.
Figura 11 Comparación coeficientes de descarga CD. Modelo numérico vs. USBR
Las pilas y los estribos en el azud inciden directamente en la contracción de la lámina de agua en su paso por la gola aumentando la acción de los esfuerzos cortantes y las pérdidas de carga por la acción del cambio de la dirección de las líneas de corriente. Así, se observa que la mayor variación porcentual del coeficiente de descarga se presenta para una carga inicial de 0,142 m, medida en el modelo numérico. Esta variación puede ser explicada en términos de la longitud efectiva que se tuvo en cuenta para el desarrollo del modelo bidimensional, por un lado, en el modelo hidráulico, se consideró la longitud efectiva teniendo en cuenta el efecto de las pilas y los estribos en el azud. No obstante, en el modelo numérico el parámetro L se mantuvo constate, es decir los caudales descargados se calcularon para una longitud efectiva de 57 m.
De igual forma se calcularon los coeficientes de descarga y se compararon con los obtenidos mediante el numérico teniendo en cuenta la carga hidráulica inicial más la altura de velocidad (figura 12).
Se evidencia claramente la tendencia que presentan los coeficientes para Rehbock y Kramer con variaciones significativas con respecto a los coeficientes calculados en el modelo numérico y a la curva establecida por la USBR. En la figura 13 se presenta la comparación de la curva de descarga entre el modelo numérico y la obtenida por Ingetec.
En el análisis del coeficiente descarga para una elevación parcial del labio de la compuerta radial se utiliza la ecuación (5), que depende de la forma y posición de la compuerta y de la apertura con respecto al azud, originando una variación del coeficiente de descarga C en función de la altura de operación H e y la descarga del vertedero.
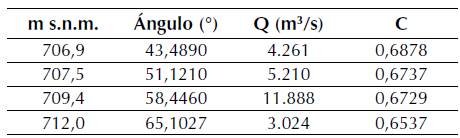
En la figura 14 se presenta los valores para el coeficiente de descarga C comparados con los valores teóricos propuestos por la USBR. Para una elevación máxima del labio de la compuerta de 712 m s.n.m. se obtuvo un coeficiente de descarga de 0,6537 para un caudal de 73,8 lps, el cual representa la 3024 m3/s para el vertedero El Quimbo. Se evidencia una variación del caudal del 4,253 % para la cota 705,629 m s.n.m. con respecto a los valores calculados. La tabla 5 presenta los valores del coeficiente de descarga C para la apertura variable de compuertas del modelo numérico.
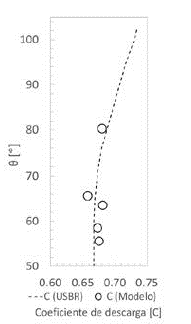
Fuente: elaboración propia.
Figura 14 Coeficientes de descarga C para apertura variable de compuertas
Coeficiente de fricción
El coeficiente de fricción es un parámetro adimensional definido como la relación de la tensión de corte de la pared y la presión dinámica de referencia. ANSYS Fluent determina el coeficiente de fricción con base en la densidad y la velocidad de referencia. La distribución del coeficiente de fricción sobre la pared de la gola muestra que para la relación H/HD=0,5 el menor valor se establece en X=0,15HD correspondiente a C f =0,25, de igual forma, para la relación H/HD=1,33, se indica un C f =0,62 en X=-0,02HD, esto se experimenta instantes antes de la entrada del flujo a la compuerta, una vez el fluido supera el paso por la compuerta el coeficiente de fricción aumenta a 2,82 en la posición 0,325HD.
De igual forma, en el comportamiento del coeficiente de presión, este estudio demostró que a medida que la carga hidráulica aumenta con respeto a la carga de diseño, se incrementarán los esfuerzos cortantes en la vecindad entre la gola y la salida de la compuerta.
CONCLUSIONES
La validación del modelo numérico (VOF) se llevó a cabo en términos de la comparación de la lámina de agua, la presión y los valores para los coeficientes de descarga del modelo numérico con los calculados por Ingetec y la Universidad Nacional de Colombia (sede Manizales). Así, el modelo numérico encontró que para un caudal de 73,77 lps, con una elevación del labio de la compuerta de 724,6 m s.n.m., bajo condiciones de flujo permanente, se alcanzó convergencia después de 809.843 iteraciones, con una variación final de flujo másico del 0,277 %, lo cual garantiza la continuidad tanto en la entrada como en la salida del caudal de volumen de control.
La presión con respecto a la carga hidráulica (H) y la carga de diseño (HD) y teniendo en cuenta la relación de diseño (H/HD=1,33) sobre la gola en X=-0,175HD, se establece un valor crítico para la cavitación de hp=-0,165HD, lo que concuerda con lo indicado por la USBR. Cuando la carga hidráulica supera la carga de diseño, la trayectoria de la lámina de agua será más alta en la cresta, creando presiones negativas, resultando en el aumento de la presión en la descarga aguas abajo de la estructura. Así, el grado de cavitación potencial encontrado corresponde según este estudio a una cavitación incipiente, la cual no afectará nivel estructural el vertedero.
Se evidencia que la presión para H/HD=0,505 sobre la gola en x=-0,1HD es aproximadamente cero. La presión mínima para H/HD=1,0 es hp=0,25HD con una ubicación en -0,08HD. Es decir, a medida que la relación H/HD aumenta, la presión aumenta aguas abajo del vertedero.
Una vez el flujo supera el estado subcrítico en su paso por la gola a estado supercrítico en la rápida, se inicia el desarrollo completo del perfil de velocidades, lo cual genera una velocidad en la rápida de 4,38 m/s para la abscisa 4,3 m y un caudal de 72,5 lps. De igual forma, se evidencia el comportamiento curvilíneo del perfil de velocidades de acuerdo con los principios teóricos que aplican para flujo en canales abiertos.
El modelo numérico demostró que la fluctuación de la presión dinámica a lo largo del vertedero permanecerá positiva siempre y cuando el nivel del embalse esté por debajo de la creciente máxima probable.
La presión obtenida en el deflector a partir del modelo numérico es de 31,766 m.c.a., esta medición se realizó en un punto análogo al modelo hidráulico. Por su parte, Ingetec estableció para el piezómetro (P4) una lectura de 32,9 m.c.a., con una variación de 3,44 %. Asimismo, en la salida del flujo del deflector se experimentó un comportamiento característico de la presión generando presiones inferiores a la presión atmosférica de 23 Pa. Este comportamiento se evidenció para los diferentes caudales modelados y para aperturas variables de las compuertas.
Este estudio comprobó que la relación entre la carga hidráulico con respecto a la carga de diseño no debe superar 1,33, lo cual a su vez concuerda con lo recomendado por la USBR. En el diseño de vertederos la relación H/HD incide de manera directa en la aparición de fenómenos de cavitación sobre la estructura, en el desarrollo de altas velocidades en la rápida, en el deflector y en la capacidad de descarga del vertedero. Así las cosas, se debe establecer una aproximación de la relación entre la carga hidráulica y la altura de diseño cercana a 1, esto disminuirá las subpresiones en la gola y en el deflector, y reducirá las velocidades en la estructura. Para lograr esto la estructura debe adoptar el perfil característico de la lámina de agua a la salida de la gola.
Por último, se recomienda para el desarrollo de futuros estudios CFD, evaluar el grado de refinamiento de la malla en la apertura y cierre de la compuerta, el análisis del acoplamiento del sistema y la construcción del perfil de movimiento, debido principalmente a la variación del comportamiento físico de la compuerta en función del tiempo, lo cual genera cambios en el dominio. Este comportamiento dinámico se puede modelar mediante los esquemas de suavizado, estratificación y remezclado disponibles en ANSYS Fluent.