Spanish (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
Introducción
En el interior de los materiales sometidos a esfuerzos se generan ondas elásticas producidas por la deformación del material y otras fuentes, como las debidas al crecimiento de fisuras, movimiento de dislocaciones, rotura de inclusiones, etc. La técnica de emisión acústica (EA) permite obtener información de estos procesos, detectar y medir estas ondas con sensores piezoeléctricos que transforman la señal mecánica en señal eléctrica. Las ondas elásticas provenientes del interior del material son registradas sobre la superficie, donde se ubican los sensores piezoeléctricos. Estas señales, en la forma de ráfagas llamadas hits, son procesadas para su posterior análisis. La señal eléctrica de EA es de muy baja amplitud (10 µV) y de alta frecuencia (50 kHz a 1 MHz). Como se ilustra en la figura 1, exhibe eventos discretos con forma de pulsos oscilantes que alcanzan una amplitud máxima en un tiempo de subida (rise time) de la señal, para luego amortiguarse.
El equipo de EA (figura 2) cuenta con una placa electrónica que se encarga de la toma de las amplitudes de la señal en función del tiempo, con lo cual es posible observarla forma de onda de la señal; más tarde la placa procesa esta información y computa los valores de los parámetros característicos de la señal: energía, valor cuadrático medio (valor RMS), amplitud, rise time, duración del evento, etc. Esta técnica de EA proporciona un método para caracterizar los daños que sufre el material cuando es llevado a la rotura y dar cuenta, entre otros, de los procesos de microfisurado, crecimiento de fisuras y, por último, la coalescencia en macrofisuras hasta la rotura final del material.
Desde la década de 1960 se registran artículos sobre fractura de rocas sometidas a compresión (Hoek y Bieniawski, 1965; Lockner, 1993; Scholz, 1968) y es también un tema de actualidad por sus aplicaciones (Mirmohammadlou, Memarian, Mohammadi y Jafari, 2017). Resulta interesante observar que la EA es generada en distintas escalas espaciales y temporales abarcando desde la ruptura de ligaduras atómicas hasta fallas sísmicas. Por ello, la información sísmica y la EA son complementarias, tanto en sus aplicaciones como en su base teórica. A partir de esta idea, para dar cuenta de los procesos de daño en un material rocoso sometido a esfuerzos, hay trabajos (Carpinteri, Lacidogna y Puzzi, 2009; Rao y Prasanna Lakshmi, 2005; Shiotani, Yuyama, Li, y Ohtsu, 2001; Zhang, 2018) que estudian el valor del b-value. Este parámetro surge de la distribución del número acumulado de hits de EA en función de su respectiva amplitud. Se comprueba que la relación en escala log-log es lineal y es conocida su aplicación en la sísmica como ley de Gutenberg-Richter.
Metodología
Diseño experimental
Siguiendo el trabajo de Filipussi et al. (2015), se ensayaron cuatro probetas cilíndricas de 75 mm de diámetro y 150 mm de largo, sobre testigos de andesita extraídos in situ de roca del Cerro Blanco, provincia de San Juan, Argentina. Estas probetas fueron ensayadas a compresión simple uniaxial y llevadas a la rotura. Se utilizó una máquina marca CGTS de 100 toneladas de capacidad, de tipo servohidráulica y lazo cerrado donde se impuso una velocidad de desplazamiento de actuador de 0,12 mm/min. La figura 3 muestra el arreglo experimental de una probeta de andesita instrumentada con sensores de EA.
Se emplearon tres sensores piezoeléctricos para monitorear la EA. En la superficie de la probeta se colocaron dos sensores, uno sintonizado a 60 kHz y otro a 150 kHz. Al tercero, de banda ancha, se lo adhirió al plato de carga inferior teniendo en cuenta la propiedad de buena guía de onda del metal involucrado. El equipo de EA se completó con una placa de dos canales PCI - 2 de PAC (Physical Acoustic Corporation) y se utilizó el software comercial AEWIN para el análisis y determinación de la mayoría de los parámetros característicos de las señales.
Modelo de fractura. Frecuencia esquina
D. Filipussi, Piotrkowski, y Ruzzante (2012) simulan una señal de EA cuya fuente es una fisura que se propaga en un medio material frágil, homogéneo e isótropo, a partir de un modelo de fractura cuyos fundamentos provienen de la geofísica (Aki y Richards, 1980). La duración del evento de EA, su amplitud y tiempo de subida son estimados por el modelo y se relacionan con características de la fuente. El análisis del espectro de Fourier de la señal de EA obtenida del modelo está dado por la ecuación (1).
Donde,
es la transformada de Fourier del campo de desplazamiento; Uo, el valor máximo alcanzado por la discontinuidad del desplazamiento en la fractura; A, el área de la fractura; T, el tiempo en alcanzar la discontinuidad un 63 % de Uo, y (o, el tiempo de subida de la señal a detectar. En el espectro teórico determinado por el modelo se observa que la señal es constante a bajas frecuencias y luego decrece a frecuencias más altas con la inversa del cuadrado de la frecuencia. La frecuencia de encuentro de estas dos tendencias del espectro en una escala log-log se denomina frecuencia esquina f
c
. El modelo predice también que la longitud de la fractura es inversamente proporcional a la frecuencia esquina y está dada por la ecuación (2).
Donde, L es la longitud de la fisura;
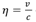es la proporción entre la velocidad v de avance de la fractura y la velocidad 𝑐 de onda del sonido en el medio material (( vale cerca de 1 para un material frágil); ( es el ángulo de detección respecto a la línea de avance de la fractura.
En este trabajo se estimó la longitud de las fisuras con esta última ecuación, a través de la medición de las frecuencias esquinas de las señales adquiridas en los instantes de tiempo en que la energía del hit alcanza valores máximos relativos. Se consideró que ( = 0.7 por ser el material frágil, que la detección fue aproximadamente en la línea de avance de la fractura ( ( = 0º) y que la velocidad de propagación de onda en la andesita es
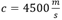como se menciona en Schön (2011).
En la figura 4 se muestra un hit y en la figura 5 su correspondiente espectro en escala log-log, donde se indica la frecuencia esquina determinada por el punto de intersección de las tendencias a baja y alta frecuencia.
Fuente: elaboración propia.
Figura 5 Espectro de Fourier de un hit en escala log-log con frecuencia esquina 302,1 kHz
Los hits seleccionados para la obtención de la frecuencia esquina corresponden a aquellos intervalos de tiempo donde el valor cuadrático medio RMS de las señales alcanza un máximo relativo, como se muestra en la figura 6.
La tabla 1 detalla los valores de frecuencia esquina determinados para los tiempos indicados que corresponden a un intervalo de tiempo que contiene a un máximo relativo de RMS.
Tabla 1 Frecuencia esquina y su correspondiente longitud de fisura
| Tiempo (s) | Frecuencia Equina (kHz) | Longitud de la fisura (mm) |
|---|---|---|
| 615,60 | 239,6 | 5,53 |
| 615,74 | 302,1 | 4,39 |
| 615,88 | 197,9 | 6,70 |
| 616,02 | 270,8 | 4,89 |
| 616,18 | 302,1 | 4,39 |
| 616,34 | 354,2 | 3,74 |
| 616,52 | 270,8 | 4,89 |
| 616,73 | 291,7 | 4,54 |
| 616,91 | 302,1 | 4,39 |
| 617,18 | 291,7 | 4,54 |
Fuente: elaboración propia.
Transformada Wavelet continua
La transformada wavelet continua (continuous Wavelet transform, CWT) permite, como la transformada de Fourier, estudiar las componentes de frecuencia de una señal. Además, brinda información acerca de la localización temporal de dichas componentes. Siguiendo la exposición de Boggess y Narcowich (2009), se considera una función Wavelet ((t) que cumpla con los requisitos de ser continua, tener decaimiento exponencial e integral nula en
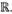. Bajo estas condiciones, la CWT de una función
es la función
definida por la ecuación (3).
En el caso en que a ( 0, mientras que W f (0,b) = 0. La integral definida por la ecuación (3) compara la función f(t) con la Wavelet ((t) después de un cambio de escala y una traslación temporal. De esta forma, el valor W f (a,b) mide la componente en frecuencia de la señal f(t) proporcional a (1/a) y localizada en torno al tiempo b.
En el presente trabajo se utilizó la Wavelet de Morlet definida por la ecuación (4).
Los detalles de implementación de la CWT para señales discretas pueden consultarse en el trabajo clásico de Torrence y Compo (1998). En la figura 7 se ilustra uno de los hits estudiados y en la figura 8 su correspondiente escalograma, es decir, un gráfico de la densidad de energía Wavelet correspondiente a cada tiempo y frecuencia.
A partir de la transformada Wavelet de una señal pueden filtrarse las frecuencias indeseadas eliminando los coeficientes correspondientes y reconstruyendo la señal. En la figura 9 se ilustra el hit anterior filtrado entre 240 kHz y 300 kHz, y en la figura 10, su correspondiente escalograma.
Aplicación al ensayo
Al aplicar la CWT a cada hit registrado en el ensayo se conocen sus componentes de frecuencia localizadas en el tiempo. El gráfico de la figura 11 representa para cada hit la frecuencia de mayor energía. En el eje vertical se expresa la frecuencia en kHz y en el eje horizontal el tiempo real en segundos de ocurrencia del hit durante el ensayo. Se aprecia que las componentes de mayor frecuencia se manifiestan hacia el final del ensayo.
Tabla 2 Conteo de hits a diferentes frecuencias
| Frecuencia (kHz) | Cantidad de hits |
|---|---|
| 88 | 6 |
| 104 | 7066 |
| 123 | 21386 |
| 146 | 6589 |
| 173 | 10373 |
| 205 | 12769 |
| 242 | 15603 |
| 287 | 1527 |
| 340 | 66 |
| 403 | 1 |
Fuente: elaboración propia.
Las dos frecuencias para las cuales se alcanza más veces el máximo de energía son 123 kHz y 242 kHz. La figura 12 se obtuvo después de filtrar los hits para valores próximos a la frecuencia esquina: entre 240 kHz y 300 kHz. Una vez más, se indica la frecuencia a la que cada hit alcanza su máxima energía. En esta ocasión, se agrega un círculo cuyo diámetro y color responden al nivel de energía alcanzado. Aunque no es concluyente, se aprecia cierta tendencia a que los hits más energéticos se den hacia el final del ensayo.
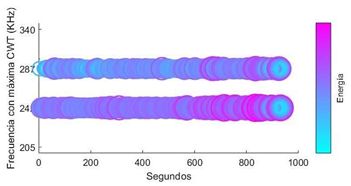
Fuente: elaboración propia.
Figura 12 Frecuencias características luego de filtrar en base a la frecuencia esquina
Wavelet energy b-value
Siguiendo a Sagasta et al. (2018), se presenta una adaptación de la ley de Gutenberg-Richter usada en sismología. En este contexto, la EA se interpreta como sismología de pequeña escala. Para ello se considera la energía wavelet (AEE) de cada señal reconstruida luego del filtrado (ecuación (5)).
Luego se la vincula con la cantidad N de hits cuya energía supera un valor dado de AEE. La figura 13 ilustra esta relación para la probeta del ensayo, con los hits reconstruidos luego del filtrado entre 240 kHz y 300 kHz. Para cada hit representado se asigna además un color que indica su ocurrencia en el tiempo. Una vez más se aprecia que los hits de mayor energía ocurren hacia el final del ensayo.
Como sugiere el gráfico, se puede postular una relación lineal entre los logaritmos de estas variables (ecuación (6)).
El Wavelet energy b-value (bWE) se define justamente como el valor b E de esta fórmula. Un valor grande de b E indica una rápida variación de N con respecto a la energía, lo cual representaría un régimen de fractura estable. Esto es usualmente indicativo de una gran cantidad de eventos de energía relativamente baja, lo cual es consistente con procesos de creación de microfracturas o de crecimiento lento de fracturas. En cambio, un valor pequeño de 𝑏 𝐸 indica una variación brusca de energía en pocos hits, lo que sugiere la formación de macrofracturas o crecimiento rápido de fracturas. Es importante identificar los valores de energía para los cuales se alcanzan mínimos locales del índice. La figura 14 ilustra las rectas de cuadrados mínimos obtenidas al dividir el intervalo de 𝐴𝐸𝐸 en subintervalos de igual longitud y calcular 𝑏 𝐸 en cada uno de ellos. La figura 15 muestra el bWE obtenido para distintos subintervalos.
Resultados
La frecuencia característica obtenida mediante la CWT resulta consistente con los resultados para la frecuencia esquina (ver tabla 2, donde se hace el conteo de hits a diferentes frecuencias).
El estudio de la evolución del bWE para las distintas bandas de frecuencia sugiere la existencia de energías características que se pueden asociar a distintos mecanismos de fracturas en las rocas. Los mínimos locales de bWE (figura 15) identifican estos valores críticos de AEE.
Conclusiones
A partir de un ensayo de una probeta de andesita bajo compresión uniaxial llevada a la rotura y del registro de EA mediante un sensor de banda ancha, se pudo identificar en los hits de mayor energía una frecuencia esquina del orden de 300 kHz que se correspondió con una longitud de fisura del orden de 5 mm.
Los resultados obtenidos con el análisis Wavelet permiten una mayor precisión en la determinación de frecuencias características, que fueron 123 kHz y 242 kHz, siendo esta última consistente con la frecuencia esquina. La combinación de ambos criterios, frecuencia esquina y máximo de energía de la CWT permitió, filtrando entre 240 kHz y 300 kHz, encontrar con precisión las frecuencias de 242 kHz y 287 kHz que se podrían asignar a mecanismos de fractura. El bWE calculado en la banda 240-300 kHz permitió hallar, mediante la localización de mínimos locales, valores críticos de energía que identificarían la aparición de macrofisuras. Los hits de mayor energía se manifiestan preponderantemente hacia el final del ensayo.
