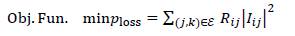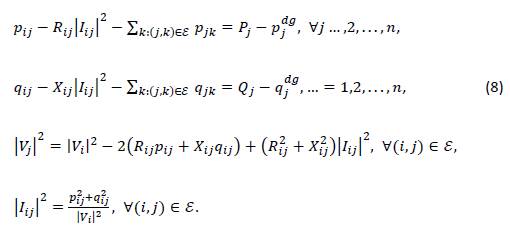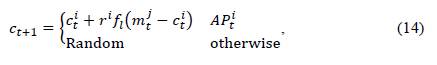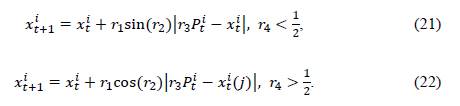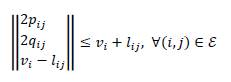1. INTRODUCTION
Electrical distribution networks are the largest part of an electrical system and are responsible for providing electricity to all the end users at medium- and low-voltage levels (Rupolo & Mantovani 2019; Rupolo et al., 2020; Hernández et al., 2021). They usually have a radial configuration, with only one central power source, i.e., a distribution substation (Devabalaji et al., 2015; Zuluaga-Ríos et al., 2021). Radial structures are preferred since their investment's costs are low and their protection schemes are simply coordinated (Lavorato et al., 2012; Velez et al., 2014). Nowadays, distributions networks have been adapted for the massive inclusion of renewable technologies, mainly photovoltaic and wind systems, as well as for battery energy storage systems (Ortiz & Kasmaei, 2019). The inclusion of these devices has drastically changed the steady-state behavior of these grids, as the uncertainties in renewable generation require real-time operation tools to guarantee the network's optimal operation (Mohagheghi & Alramlawi 2018; Tang et al., 2017). The main challenge faced by these real-time systems is to solve the optimal power flow problem (OPF) with short processing times while ensuring high-quality solutions (Mohagheghi et al., 2018). The OPF problem essentially implies an optimization procedure where the outputs of the distributed generators (DGs) are adjusted to reduce an objective function, typically power loss minimization (Grisales-Noreña et al., 2018), operative costs reductions (Tamilselvan & Jayabarathi 2018), or greenhouse gas emissions minimization (Montoya et al., 2020c). This process finds a steady-state operating point that fulfills operating constraints and satisfies the demand of the whole system. In the specialized literature, the OPF problem is addressed using two main routes: i) metaheuristic optimization (Ebeed et al., 2018), and ii) exact mathematical optimization (Molzahn & Hiskens 2016; Montoya et al., 2022). The first of these works with nature- or physics-inspired algorithms in order to determine the optimal power outputs in DGs, which are used as inputs in conventional power flow methods (Montoya et al., 2020b). This strategy is known in the literature as the master-slave optimization strategy, which is largely adopted in optimization problems where power flow solutions are required (Grisales-Noreña et al., 2018). Table 1 reports the most common metaheuristic methods for addressing the OPF problem.
Table 1 Methods used in OPF analysis that involve distributed generation
Source: Authors
The second case (exact mathematical optimization) deals with the OPF problem by restructuring the power balance constraints into convex equivalents in order to ensure that the global optimum is found (Boyd & Vandenberghe, 2004). This restructuring has great advantages, which are described below:
Convex optimization ensures uniqueness in the solution and the global optimum for the model with well-defined conditions. This is not only interesting with regard to the theoretical formulation, but also in practical terms because, in general, the global optimum is always a desired point in any problem.
Convex optimization also has algorithms with high computational efficiency, which makes it suitable for real-time applications. Furthermore, this formulation can ensure the convergence of the problem under well-defined conditions.
The main convex formulations are semidefinite programming (Bai et al., 2008), and second-order cone programming (SOCP) (Yuan & Hesamzadeh, 2019). These methods transform power balance equations into convex affine constraints, thus allowing to efficiently solve the OPF problem via interior point methods (Benson & Umit, 2013).
The two slopes mentioned above for addressing the OPF problem in distribution networks with high penetration of distributed generation originate the following research question:
Which OPF approach is more efficient and reliable?
This paper compares multiple literature results regarding OPF analysis and the SOCP reformulation of the OPF problem in order to address this question. Numerical results show that the convex optimization approach is a better way to address OPF problems in distribution networks than metaheuristic techniques, as they do not require any parametrization or statistical tests to find the solution. In addition, SOCP ensures that the global optimum is mathematically found, as was demonstrated in Farivar and Low (2013). However, in some cases, it is not possible to use software to implement convex model, which is why it is also important to study metaheuristic techniques.
This study is organized as follows: Section 2 presents the general OPF formulation using the branch of the network; Section 3 presents a general review of metaheuristic optimization methods to solve the OPF problem, which summarizes them through a pseudo-code; Section 4 shows the exact nonlinear OPF model's reformulation into a SOCP equivalent by using the hyperbolic relaxation of the power flow in each distribution line; Section 5 presents the main characteristics of the employed test feeders, composed of 33 and 69 nodes; Section 6 analyzes the results of the metaheuristics and convex optimization for solving OPF problems; and Section 7 presents the main conclusions derived from this study, as well as some possible future works.
2. EXACT OPF FORMULATION
The OPF problem for electrical distribution networks is one of the most classic optimization problems in electrical engineering (Mohagheghi et al., 2018; Khan & Singh, 2017). This problem deals with determining the subset of power injections in distributed generators aiming to minimize the total grid power losses. This is generally done for peak load conditions in particular (Grisales-Noreña et al., 2018). The main complication of this problem is its nonlinear and non-convex structure (Montoya et al., 2022; Lavaei & Low, 2011). Here, an OPF formulation is presented which is based on the branch power flow formulation that can only be applied to distribution networks with a radial configuration (Farivar & Low, 2013).
To obtain the branch OPF model, let us consider the single-line diagram presented in Figure 1. In this figure, the variables and parameters have the following meaning: 𝑃𝑖𝑗 and 𝑞𝑖𝑗 represent the active and reactive power flow from nodes 𝑖 to 𝑗, leaving from node 𝑖;𝑅𝑖𝑗 and 𝑋𝑖𝑗 correspond to the resistance and reactance parameters of the line; 𝑃𝑗𝑑 and 𝑄𝑗𝑑 are are the demand consumptions in node 𝑗, respectively; 𝑃𝑗𝑑𝑔 and 𝑄𝑗𝑑 are the active and reactive power generation in node 𝑗; 𝑉𝑖 and 𝑉𝑗 are the voltage profiles at nodes 𝑖 and 𝑗; 𝑝𝑗𝑘 and 𝑞𝑗𝑘 are the active and reactive power flows leaving from node 𝑗; and 𝐼𝑖𝑗 represents the current that flows from nodes 𝑖 to 𝑗. Note that 𝐼𝑖𝑗 and 𝑉_𝑖 are variables in the complex domain.
Based on Figure 1, the active and reactive power balances at each node are defined, except in the reference (slack source), i.e., ∀𝑗∈𝒩≠{0}, as follows:
where ℰ is the set that contains all the nodes of the network. Note that, for each distribution line, it is known that:
with 𝑍𝑖𝑗=𝑅𝑖𝑗+𝑖𝑋𝑖𝑗.. In addition, from Tellegen's theorem, the power flow in each line can be defined as follows:
Now, by substituting Equation (4) into (3) and taking the magnitude square of this expression, the following is obtained:
In addition, from Equation (4), it is known that:
The formulation of the objective function of the OPF problem is typically assigned as the minimization of power losses in all the branches of the network, which can be formulated as:
The mathematical formulation (1) to (7) defines the OPF formulation in general terms using the branch power flow formulation as presented in Montoya et al. (2022). For the sake of simplicity, it is herein presented it in compact form:
Exact nonlinear OPF model (Model 1):
Sub. To.
The main complication in the OPF model (8) corresponds to the nonlinearity introduced by the division of the square of the apparent power and the magnitude of the voltage profile, as this implies a strong non-convexity of the solution space, which makes it impossible to ensure that the global optimum is found via conventional optimization techniques. To address this complication in the optimization model, the literature shows two ways to solve this problem. The first path is to combine metaheuristic techniques by means of classical power flow methods in order to solve the problem iteratively. The second one is reformulating the problem via convex optimization in order to ensure that the global optimum is found through interior point methods.
Remark 1. The main goal of the OPF model defined in (8) is to define the set of active and reactive power generations in distributed power sources, i.e., the best values for 𝑝𝑗 𝑑𝑔 and 𝑞𝑗 𝑑𝑔 that allow minimizing the total grid losses (Farivar & Low, 2013).
3. SOLUTION WITH METAHEURISTICS
Metaheuristic optimization techniques are essentially nature-inspired optimization methods that deal with nonlinear non-convex large-scale optimization problems by using a sequential programming structure. These approaches can be classified into two big fields based on their initial inspiration. The first set includes bio-inspired algorithms such as genetic algorithms (Moradi & Abedini, 2012), particle swarm optimization (Grisales-Noreña et al, 2018), the artificial bee colony algorithm (Deshmukh & Kalage, 2018), the krill herd algorithm (Mukherjee & Mukherjee, 2015), the teaching-based learning optimizer (Bouchekara et al, 2014), ant colony optimization (Raviprabakaran & Sunramanian, 2018), and the bat algorithm (Yuan et al, 2017), among others. The second field includes physics- and mathematics-inspired methods such as black hole optimization (Hasan & Hawary, 2014), the supernova optimizer (Hudaib & Fakhouri, 2018), the vortex search algorithm (Yuan et al, 2017), the hurricane search algorithm (Rhoub & Imrani, 2014), the sine-cosine algorithm (Attia et al., 2018; Mirjalili et al., 2019), and so on.
The main characteristics of optimization methods based on metaheuristics are listed below:
They work with an initial population that contains some of the problem's decision variables, i.e., active and reactive power generation in distributed sources, in the case of the OPF problem.
The objective function is modified into a fitness function that considers restrictions as penalties in order to explore possible infeasible regions that allow reaching promissory regions in the solution space with high-quality solutions.
A slave stage is typically used to address the problem associated with equality constraints, i.e., the power flow solution in the case of OPF analysis.
These use evolution criteria to explore and exploit the solution space, i.e., in the genetic algorithm, the evolution stage uses selection, recombination, and mutation criteria.
Two typical stopping criteria are used for finishing the exploration of the solution space: i) when the maximum number of iterations is reached, and ii) when, during k max consecutive iterations, the best solution does not show any improvement. In general, the main advantage of using metaheuristics optimization methods is their easy implementation in any programming language while using scalars, vectors, and matrices to represent the problem. However, the main problems experienced with metaheuristics are i) the optimal parametrization of the problem, i.e., the number of iterations and size of the population, among others; and ii) the need to perform statistical analyses, as it is not possible to mathematically ensure that the global optimum is found.
Regarding the application of metaheuristics to OPF solutions, tens of methods can be found in the current literature, which are also combined with optimal siting and sizing strategies for distributed generation. Table 1 reports some common approaches available in the literature for OPF analysis. In general, the application of a metaheuristic optimization method to solve the OPF problem described in (8) can be summarized as presented in Algorithm 1.
The main aspect of Algorithm 1 is the evaluation of the fitness function, which, in the case of OPF analysis, is related to the power flow solution. The power flow solution is typically used as an iterative approach. Some of the most common power flow methods are the Gauss-Seidel, Netwon-Raphson, and graph-based methods (Montoya & Gil-Gonzalez 2020; Shen et al., 2018) and successive approximations (Montoya & Gil-Gonzalez, 2020), among others. The power flow solution defines the direction in which the solution space will be explored in order to find a high-quality solution.
3.1. POWER FLOW SOLUTION
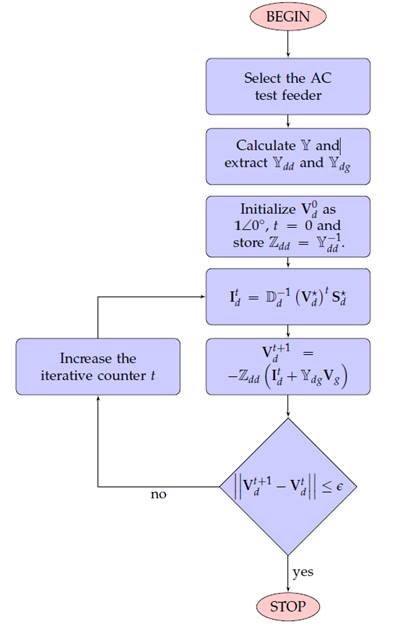
Because metaheuristic methodologies employ a master-slave type strategy to solve the OPF problem, in which each set of generated powers must be evaluated by a power flow, this research employs the successive approximation method (Montoya & Gil-Gonzalez, 2020). The main features of this method are presented in the flow diagram shown in Figure 2.
It is important to mention that, in this Figure, which shows the sequence of steps to solve the power flow problem in radial or meshed distribution networks with a single-phase equivalent, the variables and parameters presented therein have the following interpretation: 𝕐 is a matrix defined in the complex domain containing the nodal admittances of the system; 𝕐𝑑𝑔 is a submatrix derived from 𝕐 and corresponds to the section of the network related to the slack node; 𝕐𝑑𝑑 is also a submatrix of 𝕐 that corresponds to the demand nodes of the network; 𝑉𝑑 0 corresponds to the demand nodes in the network; 𝑉𝑑 𝑡+1 corresponds to the unknown voltage variables of all the load nodes present in the network; ℤ𝑑𝑑 is the inverse matrix of 𝕐𝑑𝑑 and corresponds directly to the demand impedances of the network; 𝐼𝑑 is the vector containing the network demand currents; 𝐷𝑑 −1(𝑉𝑑 ∗) is the inverse diagonal of the transposed nodal demand voltages; and c refers to the constant defining the stop criterion, usually with a value of 1𝑥10−10.
Once the power flow problem has been solved using the successive approximation method (Figure 2), the grid power losses can be calculated as follows:
Source: Authors
Figure 2 Flowchart of the proposed power flow method based on successive approximations
where 𝕊loss corresponds to the total apparent power losses of the network.
3.2. IMPLEMENTING THE METAHEURISTIC OPTIMIZERS
To generate the power set (i.e., implementing the master stage of the optimal power flow problem), the following metaheuristic methods are employed: particle swarm optimization (Lima & Barán, 2006), the crow search algorithm (Prior et al., 2008), genetic algorithms (Winter, 2005), the sine-cosine algorithm (Rosli et al., 2020), the vortex search algorithm (Doğan & Ölmez, 2015), and the black hole optimizer (Grisales-Noreña et al., 2020).
The main characteristic of these combinatorial optimization methods is that they all explore and exploit the solution space starting from an initial population. This population is essentially the starting point for the algorithm and is generally created randomly throughout the solution space. This population can be mathematically represented as follows:
where 𝑃𝑔𝑑 min and 𝑃𝑔𝑑 max define the capacity limits of distributed generation, and r is a matrix of random numbers with dimensions 𝑛𝑖 rows (number of individuals) and 𝑛𝑔𝑑 columns (number of distributed generators).
Once the initial population is established, the implementation methodology is executed for each of the metaheuristic optimization methods. The work logic of each of the methodologies analyzed in this research is explained below.
3.2.1. PARTICLE SWARM OPTIMIZATION
Particle swarm optimization (PSO) is a metaheuristic method based on the behavior of particles in nature. It especially focuses on the behavior of flocks of fish and birds (Lima & Barán, 2006). These particles move within the search space while obeying a set of rules that consider their position and velocity in order to find global maximum or minimum values (Gutiérrez et al., 2017). In PSO, the population considers n particles corresponding to candidate solutions. These particles are a vector of m-dimensional with real values, where m represents the number of optimized parameters. This indicates that each dimension of the particle is a parameter of the problem space to be optimized. In each iteration of the execution process, the information of each particle is considered, as well as all the information associated to the swarm. With this, the evolution of the swarm and the update of the global minima that will determine the best solution for the objective function is achieved. Once the initial population is generated as denoted in Equation (10), positions 𝑥𝑡 𝑖 and speeds 𝑣𝑡 𝑖 are established in the particle swarm. Each particle knows the best position it has visited (𝑃best). This variable works as an autobiographical local memory, and the best position of the leader 𝐺best works as a local memory that is determined by the best places visited in the past by the whole group or swarm. The leader is the particle that presents the best adaptation function in each iteration. The velocity and position function of each particle at iteration t + 1 are given by the following formulations:
where 𝑤𝑡 represents the inertia factor, which in turn represents the degree of influence of the current speed in the future speed and is responsible for controlling the convergence of the algorithm; 𝜙1 and 𝜙2 control the position of the particle and the leader based on the new iteration velocity; and 𝑟1 and 𝑟2 are random number values in the range of [0,1]. The inertia factor is updated in each iteration according to the following formulation:
When the power flow has been solved and the objective function has been evaluated for each particle, the 𝐺𝑏𝑒𝑠𝑡 of each iteration is obtained, which is compared iteration after iteration to finally obtain the optimal solution to the problem.
3.2.2. CROW SEARCH ALGORITHM
The crow search algorithm (CSA) was developed by Askarzadeh (2016) and consists of an evolutionary algorithm inspired by the intelligent behavior of crows. These animals are considered to be among the most intelligent in the world (Prior et al., 2008). Crows are known to watch other birds, looking for where they hide their food in order to steal it once the owner leaves. If a crow has committed a theft, it will take extra precautions, such as changing its hiding place to avoid being a future victim. In fact, they use their own thieving experience to predict the behavior of a potential thief, so that they can determine the safest way to protect their supplies.
Based on the above, in the crow search algorithm, the population of N individuals (crows) evolves from a given point (t = 0) up to a maximum number of generations (t = 𝑡 𝑚𝑎𝑥 ). Each individual 𝑐𝑘 𝑖 (𝑖∈[1,...𝑁]) is represented by a d-dimensional vector, where each of the dimensions corresponds to a decision variable of the problem to be solved.
This algorithm considers two states for a new population 𝐶𝑡+1. The first state is when the individual knows that it is being followed by a thief, and the second is when the individual does not know. This behavior is modeled with a knowledge probability factor 𝐴 𝑃 𝑡 𝑖 that determines the state of an individual. In this way, each new individual in the population is generated as shown in Equation (14):
where 𝑟𝑖 and 𝑟𝑗 are random numbers between 0 and 1; 𝑓𝑙 is a parameter that determines the flight distance; and 𝑚𝑡 𝑗 is the memory of individual 𝑗 at iteration 𝑡, which refers to the food cache.
First, the algorithm is initialized like other metaheuristic methods, with the initial population (bounds and dimensions) and initial parameters (stopping criteria, fl, AP), in accordance with Equation (10). The next step is to randomly initialize the positions of the individuals and evaluate them based on the objective function, in order to obtain results for each individual and thus extract the best solution for the objective function. After this, the evolution (new positions) is generated via Equation (14). For all individuals, the new positions are evaluated based on the objective function, and the memory is updated. Finally, the stopping criteria for the iterative process of the algorithm are established. These are linked to the implementation of the CSA, so two stopping criteria are generally used: i) when a value of the objective function is reached in which the best individuals converge to a value and this does not change throughout the iterations, and ii) when a predetermined number of iterations is reached.
3.2.3. GENETIC ALGORITHM
Genetic algorithms (GAs) are methods based on adaptation that can be used to solve optimization search problems. These algorithms are based on the genetic processes of living organisms. By mimicking these processes, GAs are able to generate solutions to real-world problems (Winter, 2005). The optimal evolution that leads to optimal values depends on their proper encoding.
GAs work with a population of individuals, each of which represents a feasible solution to a given problem. Each individual is assigned a value, or score related to the objective function and the improvement of the results.
GAs, like the other algorithms, are linked to the implementation of the problem to be addressed, i.e., each objective function has an adapted GA. The following section shows a base algorithm that used to adapt to each optimization problem. Each genetic algorithm consists of the following stages: domain configuration, population evaluation, selection, crossover, and mutation.
Via domain coding, a set of possible input values is obtained, which refers to the domain in which the function is located. This is equivalent to the genotype, which is the DNA of the organisms (Mitchell, 1998). The algorithm obtains an initial population as input, with which new populations are generated; some individuals disappear, and others appear until a solution is reached depending on the stopping criteria.
With the evaluation of the population, there is a fitness function aiming to minimize the quadratic error E rms . When this error tends to 0, the fitness tends to 1. The correlation between this function and the E rms is denoted in Equations (15) and (16):
where E rms is the mean square error, X is the value of the target variable of the population, and n i is the amount of data for the initial population.
Afterwards, the most qualified individuals are selected for reproduction, i.e., the most qualified individuals of the initial population that will be crossed to obtain a new generation, with a hybrid code from the most qualified individuals and ambitious characteristics. The crossing begins with the selected individuals, which consists of recombining the genetic information of the two individuals (parents), which reproduce and yield a third individual (child) that shares the genetic information of the other two. It is assumed that the third individual (offspring) obtains the best adaptive characteristics of the population. Finally, there is the mutation, which is an alteration in the child's genetic code, causing one of its genes to be randomly modified. This mutation has a low probability, usually a value of less than 1% since the fitness function for mutated individuals is low.
3.2.4. VORTEX SEARCH ALGORITHM
The vortex search algorithm (VSA) is a metaheuristic algorithm inspired by the vortex flow behavior of agitated fluids (Doğan & Ölmez, 2015). The algorithm postulates candidate solutions that are generated based on the current best solution by using a Gaussian distribution in each iteration (Gharehchopogh et al., 2021), taking the current best solution as the center, i.e., the center of the hypersphere (Gil-González et al., 2020). The main characteristics of the VSA are presented below.
Generating candidate solutions using some region structures is of vital importance for the success of metaheuristics based on a central solution. When small changes are made to the current solution, the region is said to have a strong locality (Doğan, & Ölmez, 2015). In contrast, a weak locality is characterized by a large effect on the solution, which results in a random search within the search space (Doğan & Ölmez, 2015). Efficient exploration (weak locality) is required in the initial steps, and, once the algorithm converges to a near optimal solution, further exploitation (strong locality) is required to adjust the current solution towards the optimal one. This algorithm requires an initial solution considered to have a two-dimensional problem for the mathematical model (9). An outer circle of the vortex is taken, which is centered in the first search space μ 0 (center of the hypersphere) and can be calculated via Equation (17)
where X max and X min are the upper and lower bounds, respectively. They are dxl vectors that define the bound constraints of the problem whose dimension is d. Note that this dimension corresponds to the number of DGs to be dispatched in the problem under study.
Several regional solutions C t (s ) (where t represents the iteration rate, which is initially t - 0) are randomly generated around the initial solution μ 0 in d-dimensional space using a Gaussian distribution. Equation (18) shows the Gaussian distribution (Gharehchopogh et al., 2021):
where 𝑑 represents the dimension, 𝑥 is the vector 𝑑×1 composed of random variables, 𝜇 is the vector 𝑑×1 of sample means, and Σ is the covariance matrix (Scoble, 2005). For this algorithm, Σ can be calculated using equal variances with zero covariances via Equation (19);
where 𝜎2 represents the variance of the distribution, and 𝐼 represents the identity matrix 𝑑×𝑑. The initial standard deviation 𝜎0 of the distribution can be calculated through Equation (20):
It is important to mention that one of the main characteristics of the VSA is that it works with a variable radius that decreases as the solution space is explored. This, in order to control the balance between exploration and exploitation of the solution space (Montoya et al., 2020b). This research employs the exponential reduction of the radius proposed by Montoya et al. (2020).
3.2.5. SINE-COSINE ALGORITHM
The sine-cosine algorithm (SCA) is an optimization algorithm that works with trigonometric functions as a forward rule to explore and exploit the solution space (Abo-Elnaga & El-Shorbagy, 2020). As any other optimization technique, the population that will yield multiple random initial solutions is first created and evaluated regarding the objective function through the sine and cosine rules. With weighting factors, the SCA advances through the solution space iteratively, taking the best solution found up to the current iteration as reference (Rosli et al., 2020). The SCA evolution rule is presented below:
In Equations (21) and (22), 𝑥𝑡 𝑖 refers to the individual 𝑖 in iteration 𝑡; 𝑃𝑡 𝑖 is the leading individual in each iteration, i.e., the best solution in that iteration; and 𝑟1,𝑟2,𝑟3, and 𝑟4 are parameters specific to the SCA which define the behavior of the population as follows:
𝑟1 defines the direction of movement into or out from the area between the current position and the leader.
r 2 defines how far the movement must be in a range of [0, 2𝜋], as the outward movement of the area is represented by the positive part of the sine and cosine functions and the inward movement represents the negative part of these functions.
r 3 defines the weight in order to highlight (r3 > 1) or reduce (r3 < 1) the randomness of the location in the definition of distance.
r 4 , in the range [0,1], identifies the position based on the comparison between the sine and cosine functions.
Finally, the parameter r 1 can be mathematically defined as follows:
To solve the OPF using the SCA, once the initial population is established, the flow is solved, and the objective function is evaluated while considering the algorithm parameters. In each iteration, a leader representing the best solution is obtained. This process is repeated until there are no more updates in the leader's position, which constitutes a stopping criterion together with the maximum number of iterations achievable.
3.3.6. BLACK-HOLE OPTIMIZER (BHO)
This metaheuristic optimization algorithm is based on the dynamic interaction that occurs between stars and black holes (Velasquez et al., 2019). Its logic follows that applied in the particle swarm algorithm, making direct reference to the cumulus of stars to which the particles are related. It also employs a criterion of elimination and generation of stars through a heuristic approach that follows the concept of event horizon (Grisales-Noreña et al., 2020).
The BHO starts its exploration of the solution space when the initial population is created, which corresponds to the first set of stars randomly distributed in the solution space.
(Bouchekara, 2013). In the logic of the programmed algorithm, this is defined according to the number of individuals to be worked with and determined via Equation (10). When stars are in proximity to a black hole, they experience an intense gravitational force, which is why the particular behavior of each star may vary depending on its location with respect to the black hole (Bouchekara et al, 2014). This phenomenon is mathematically represented as follows:
where P BH refers to the black hole in the population and P i t represents the individual after the interaction with the black hole (Grisales-Noreña et al., 2020). Each star that crosses the event horizon is destroyed, so the survival of each one depends on its position with respect to the hole. To simulate the possibility of the star being consumed by the black hole, a mathematical formulation is used which defines the radius of the event horizon and determines the risk range for the star. This is described as follows:
where 𝑓(𝑃𝑡+1 𝐵𝐻) represents the best value obtained for the objective function of all individuals in the current population. On the other hand, the denominator represents the sum of the objective function of all individuals in the population in the current iteration.
The factor that determines whether any star crosses the event horizon depends on the relative distance between the star and the black hole:
If REH > DBH i is satisfied, a new star is then generated to replace the old one, ant the i th star is absorbed (destroyed) by the black hole.
Finally, if no update in the black hole's position is obtained by solving the flow and evaluating the objective function at each iteration, the optimal solution of the problem is reached.
4. CONVEX OPTIMIZATION
Convex optimization is a field of mathematical optimization that deals with complex optimization problems by reformulating nonlinear non-convex constraints into convex ones. This, in order to ensure that the global optimum is found via interior point methods (Boyd & Vandenberghe, 2004; Kronqvist et al., 2018). Some of the most common convex optimization problems are listed below:
Linear programming
Quadratic programming with affine constraints
Second-order cone programming
Semidefinite programming
Geometric programming
The most common methods for optimal power flow analysis are: quadratic programming (Garces, 2016), semidefinite programming (Bai et al., 2008; Montoya et al., 2017; Andersen et al., 2013), and second-order cone programming (Montoya et al., 2020c; Yuan & Hesamzadeh, 2019; Farivar & Low, 2013; Lavaei & Low, 2011; Baradar et al., 2013; Simiyu et al., 2020).
This study adopts the SOCP formulation by Farivar and Low (2013) to present the equivalent convex reformulation of the model (8). To address this SOCP equivalent, let us define the following auxiliary variables: 𝑙𝑖𝑗=|𝐼𝑖𝑗|2, 𝑣𝑖=|𝑉𝑖|2 and 𝑣𝑗=|𝑉𝑗|2. Now, let us approximate the hyperbolic relation between voltages and currents in the last equation of model (8) as a conic constraint, i.e.,
Remark 2. Note that (27) is still non-convex due to the equality symbol. However, this symbol can be relaxed to become a conic convex constraint, as recommended by Farivar and Low, (2013).
The convex equivalent of (27) takes the following form:
Now, with the relaxation presented in Equation (28), the nonlinear non-convex OPF model defined in (8) takes the SOCP form presented in (29).
SOCP reformulation of the OPF problem (Model 2)
Sub. To.
The main advantage of the SOCP reformulation presented in (29) is that it is mathematically ensured that the global optimum is found, as demonstrated by Farivar and Low (2013) which implies that no statistical tests or heuristic parametrizations are required (e.g., the number of iterations of population sizes, as is the case of metaheuristic optimization methods).
5. TEST FEEDERS
To compare the methodologies studied in this paper for OPF analysis in distribution networks regarding distributed generation along the AC grid, two conventional and widely used distribution grids were used, which are composed of 33 and 69 nodes. These grids are operated with 12,66 kV at the substation bus and have a radial structure. The single-line diagram for the two test systems is illustrated in Figure 3.
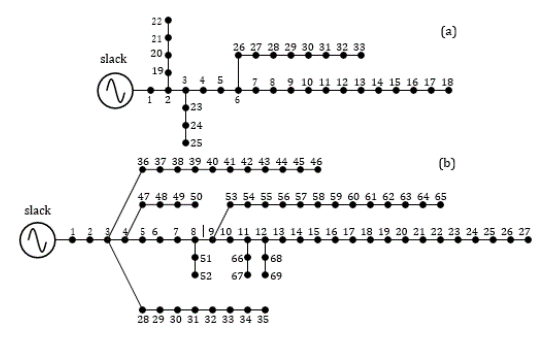
Source: Authors
Figure 3 Single-line diagram of the test feeders: a) 33- node test feeder, b) and 69-node test feeder
To evaluate the OPF solution in these test feeders, this research takes the information reported by Montoya et al. (2020) regarding the lower and upper limits of the power generated in the DGs. For the 33-node test feeder, the DGs can provide from 300 to 1.200 kW to the grid, while, in the 69-node test feeder, these outputs range from 0 to 2.000 kW. Three DGs are considered for both test feeders.
6. COMPUTATIONAL VALIDATIONS
This section compares the performance of the metaheuristics and the SOCP approaches to solve the OPF problem while considering DGs in radial distribution networks. This validation was carried out using a personal computer with an AMD Ryzen 7 3700U @ 2.3 GHz and 16 GB RAM while running a 64-bits version of Windows 10 Home Single Language and the MATLAB programming environment.
To compare these optimization approaches, the information available for both test feeders in the literature was considered (Table 2).
Table 2 Common metaheuristics used in OPF analysis
| Acronym | Optimization method | Reference |
|---|---|---|
| GA-PSO | Genetic algorithm and particle swarm optimization | (Moradi & Abedini, 2012) |
| LSFSA | Loss sensitivity factor simulated annealing | (Injeti & Kumar, 2013) |
| MINLP | Mixed-integer nonlinear programming formulation | (Kaur et al., 2014) |
| TBLO | Teaching learning-based optimization | (Sultana & Roy, 2014) |
| QOTBLO | Quasi-oppositional teaching learning-based optimization | (Sultana & Roy, 2014) |
| HSA-PABC | Harmony search algorithm and particle artificial bee colony algorithm | (Muthukumar & Jayalalitha, 2016) |
| RBFNN-PSO | Radial basis function neural network and particle swarm optimization | (Gupta et al., 2015) |
| GA-IWD | Genetic algorithm and intelligent water drops | (Moradi & Abedini, 2016) |
| AHA | Algorithmic heuristic approach | (Bayat & Bagheri, 2019) |
| KHA | Krill herd algorithm | (Sultana & Roy, 2016) |
| PBIL-PSO | Population-based incremental learning and particle swarm optimization | (Grisales-Noreña et al., 2018) |
| ABCA | Artificial bee colony algorithm | (Deshmukh & Kalage, 2018) |
| HTLBOGWO | Hybrid teaching-learning-based optimization, grey wolf optimizer | (Nowdeh et al., 2019) |
| MSSA | Mutated salp swarm algorithm | (Gholami & Paryaneh, 2019) |
| CHVSA | Constructive heuristic vortex search algorithm | (Bocanegra & Montoya, 2019) |
| GAMS | General algebraic modeling system | ( Montoya & Gil-González, 2020) |
| CBGA-VSA | Chu and Beasley genetic algorithm and vortex search algorithm | (Montoya et al., 2020b) |
Source: Authors
In order to carry out the comparison and validation processes, all the relevant information on the implementation of DG through metaheuristic optimization in each of the distribution systems under study is first collected. This, in order to observe the results obtained regarding DG size and location in the networks and perform the corresponding validations. It can be seen that, in the specialized literature, there are reports with several metaheuristic methodologies that allow reaching the goal of considerably reducing the active power losses. By observing the data, it is decided to use the node locations that yield the best results when implementing DGs. This methodology allows conducting the second part of the validation process. Once the location of the DGs is defined in the networks (nodes 13, 24, and 30 for the 33-node test feeder) and 69 (nodes 11, 18 and 61 for the 69-node grid) nodes, these positions are evaluated along with their results through validations using the selected metaheuristic methods and the SOCP methodology.
To quantitatively compare the studied methodologies for solving the OPF problem, a statistical analysis was performed in order to corroborate each of the incidence variables in the metaheuristic approaches, given the iterative nature of these methodologies and the fact that the same solution is not always reached after repeated runs. The statistical variables applied are the minimum and maximum values, the mean, and the standard deviation -all applied to the objective function after multiple runs of each of the algorithms.
6.1. 33-NODE TEST FEEDER RESULTS FOUND IN THE LITERATURE
Table 10 presents the comparative analysis between the literature reports regarding metaheuristics and the SOCP model for OPF analysis in AC distribution networks.
Table 3 Optimal location and sizing of DGs in the 33-node test feeder for the proposed and comparative approaches
| Literature information | Metaheuristics | SOCP | |||
|---|---|---|---|---|---|
| (N◦) Method | Node | Size (MW) | ploss (kW) | Size (MW) | ploss kW) |
| (1) GA-PSO | {11,16,32} | {0,9250,0,8630,1,2000} | 103,3600 | {0,6683,0,3713,0,9283} | 86,0107 |
| (2) LSFSA | {6,18,30} | {1,1124,0,4874,0,8679} | 82,0525 | {1,2000,0,4913,0,8055} | 81,8853 |
| (3) MINLP | {13,24,30} | {0,8000,1,0900,1,0500} | 72,7862 | {0,8018,1,0913,1,0536} | 72,7853 |
| (4) TLBO | {10,24,31} | {0,8246,1,0311,0,8862} | 75,5400 | {0,9746,1,0909,0,8860} | 74,5106 |
| (5) QOTLBO | {12,24,29} | {0,8808,1,0592,1,0714} | 74,1008 | {0,8799,1,0629,1,0730} | 74,1006 |
| (6) HSA-PABC | {14,24,30} | {0,7550,1,0730,1,0680} | 72,8129 | {0,7709,1,0969,1,0658} | 72,7896 |
| (7) GA-IWD | {11,16,32} | {1,2214,0,6833,1,2135} | 110,5100 | {0,6683,0,3713,0,9283} | 86,0107 |
| (8) AHA | {13,24,30} | {0,7920,1,0680,1,0270} | 72.8340 | {0,8018,1,0913,1,0536} | 72,7853 |
| (9) KHA | {13,25,30} | {0,8107,0,8368,0,8410} | 75,4116 | {0,8117,0,8712,1,0741} | 73,5036 |
| (10) MSSA | {13,24,30} | {0,8010,1,0910,1,0530} | 72,7854 | {0,8018,1,0913,1,0536} | 72,7853 |
| (11) CHVSA | {6,14,31} | {1,1846,0,6468,0,6881} | 78,4534 | {1,1892,0,6468,0,6863} | 78,4533 |
| (12) CBGA-VSA | {13,24,30} | {0,8018,1,0913,1,0536} | 72,7853 | {0,8018,1,0913,1,0536} | 72,7853 |
| (13) GAMS | {14,24,30} | {0,7550,1,0730,1,0680} | 72,8129 | {0,7709,1,0969,1,0658} | 72,7896 |
Source: Authors
The simulation results presented in Table 10 allow observing that:
The best solution reported in the literature for OPF analysis with distributed generation has been reported by the MSSA and the CBGA-VSA when nodes 13, 24, and 30 are considered as DG locations. The power losses for these methods reach 72,7853 kW as the optimal solution.
Methods such as the MINLP and the AHA have the same DG distribution. However, their optimal power flow solvers are stuck in locally optimal solutions, which are 72,7862 and 72,8340 kW, respectively. This indicates that some combinatorial methods cannot exploit the solution space adequately.
For 84,62% of the comparative methods in Table 10, the SOCP model reaches better solutions, with the greatest difference being found when the GA-IWD and the SOCP are compared, with an error of about 24,4493 kW in favor of the latter. Also note that a second big difference is observed for the GA-PSO approach.
Only two of the thirteen methods presented in Table 10 (i.e., the MSSA and the CBGA-VSA) find the global optimal solution of the problem when compared to the SOCP approach. However, it is important to mention that the power outputs in all the DGs exhibit small variations, which implies that the problem is multimodal and can have different power combinations with the same objective function.
Overall, Table 10 shows that the SOCP approach yields better solutions in the 33-node test feeder when different nodes are considered in the OPF analysis. In addition, the main advantage is that, when the combination of nodes is the same, the global optimum found is always the same, which is not possible with metaheuristics due to their random nature.
6.2. RESULTS OBTAINED BY THE 33-NODE TEST FEEDER
An initial population of 30 individuals was established, given that, after performing different tests, good comparative results were obtained regarding the objective function and the processing time. A maximum number of iterations t max of 100 was also defined for the CSA, BH, PSO, VSA, and SCA. For the GA, a number of 1.000 was defined because the execution structure requires more iterations to reach the expected value regarding the objective function. In addition, to evaluate the results obtained, each algorithm was executed 100 times in order to perform the corresponding statistical analysis.
Figures 4 and 5 show the results obtained for the global optimum or objective function and the processing time, respectively, for each of the methods implemented in the 33-node network.
The optimal size obtained, along with the best solution for each method for each of the implemented DGs, is presented in Table 4.
Table 4 Optimal DG size for each node of the 33-node test feeder
| Method | Node 13 (kW) | Node 24 (kW) | Node 30 (kW) |
|---|---|---|---|
| PSO | 801,79617 | 1.091,31399 | 1.053,60457 |
| CSA | 801,95368 | 1.091,32611 | 1.053,86541 |
| AG | 801,98661 | 1.091,73716 | 1.053,54698 |
| BH | 801,95368 | 1.091,32611 | 1.053,86541 |
| SAC | 802,32702 | 1.089,44615 | 1.053,66987 |
| VSA | 807,59058 | 1.081,81856 | 1.067,89946 |
| SOCP | 801,85244 | 1.091,42711 | 1.053,79832 |
Source: Authors
The statistical values obtained for the maximum value and standard deviation are presented in Table 5, and the average of the problem’s relevant variables for the 33-node network are presented in Table 6.
Table 5 Maximum result for the objective function and the standard deviation in the 33-node test feeder
| Method | Highest value Ploss (kW) | Standard deviation |
|---|---|---|
| PSO | 72,790363 | 0,0005063 |
| CSA | 73,997282 | 0,2162069 |
| AG | 72,707032 | 0,0003653 |
| BH | 72,787123 | 0,0028179 |
| SAC | 72,815086 | 0,0042461 |
| VSA | 73,522477 | 0,1501963 |
Source: Authors
Table 6 Average of the problem's interest variables in the 33-node test feeder
| Method | Node 13 (kW) | Node 24 (kW) | Node 30 (kW) | Ploss (kW) | Processing time (s) |
|---|---|---|---|---|---|
| PSO | 801,76408 | 1.090,97745 | 1.053,70433 | 72,785373 | 1,272468 |
| CSA | 805,91759 | 1.087,11468 | 1.028,35653 | 73,045624 | 1,348536 |
| AG | 802,33621 | 1.090,98354 | 1.053,15222 | 72,785715 | 1,274994 |
| BH | 802,02359 | 1.090,96947 | 1.053,85721 | 72,785541 | 1,156852 |
| SCA | 802,29906 | 1.088,34297 | 1.054,49701 | 72,786205 | 1,208374 |
| VSA | 800,01247 | 1.105,81499 | 1.055,56561 | 72,984163 | 1,340017 |
Source: Authors
The results obtained in the validation show that:
The best solution obtained for the objective function is reported by the SOCP method. It is also observed that the processing time for this methodology is the lowest. These results allude directly to the exact or linear structure of the SOCP, so the direct solution is obtained without iteration.
For the metaheuristic methodologies, it is observed that the best results are obtained by the GA with 72,785312 kW and BHO and PSO with 72,78513 kW. These solutions range very close to the solution obtained with the SOCP method, which shows the efficiency of metaheuristic optimization.
The implementation of the CSA shows the worst results in the validation, with 72,787761 kW. However, the range of deviation with the six remaining algorithms is very low (around 3 W). Moreover, the VSA and SCA are very close to the optimum values obtained with the SOCP reference, even though they do not yield the best results.
The processing times obtained show a trend in the results for the six metaheuristic techniques, as these values oscillate between 1,114 and 1,344 s. On the other hand, the SOCP shows better results, which is clearly due to its convexity. In general, good results are observed for this variable, which, although it is not decisive in the problem, could be considered to be a good criterion of choice for ease of processing.
A uniform sizing of DG can be observed among the various methodologies, with the first DG being of about 800 kW, the second one of 1.090 kW, and the third one of 1.053 kW. These results coincide with those reported in the analyzed literature, given that the same sizing values were achieved.
The standard deviation reported in Table 5 shows satisfactory results. The values are low, which guarantees that, after successive runs, the dispersion of the data is in a minimum range, which alludes directly to the accuracy of the methods.
The averages of the DGs sizing, objective function, and processing times are shown in Table 6. The values are in low ranges and with direct similarity to the optimum values for each method.
In general, good results can be observed regarding the penetration of DGs in the network and their implementation via metaheuristic and exact methodologies. There are reductions close to 66% in total system losses, going from 210,99 kW to about 72,7850 kW.
6.3. 69-NODE TEST FEEDER RESULTS FOUND IN THE LITERATURE
Table 7 presents the numerical comparison between some metaheuristics reported in the literature and the SCOP model.
Table 7 Optimal location and sizing of DGs in the 69-node test feeder for the proposed and comparative approaches
| Literature information | Metaheuristics | SOCP | |||
|---|---|---|---|---|---|
| (N◦) Method | Node | Size (MW) | Ploss (kW) | Size (MW) | ploss(kW) |
| (1) GA-PSO | {21,61,63} | {0,9105,1,1926,0,8849} | 84,5909 | {0,4866,0,4883,0,3003} | 71,9595 |
| (2) LSFSA | {18,60,65} | {0,4204,1,3311,0,4298} | 72,1120 | {0,5276,1,3609,0,4540} | 76,4762 |
| (3) MINLP | {11,17,61} | {0,5300,0,3800,1,7200} | 69,4090 | {0,5267,0,3802,1,7189} | 69,4088 |
| (4) TLBO | {15,61,63} | {0,5919,0,8188,0,9003} | 72,4157 | {0,5542,1,4772,0,3002} | 71,6738 |
| (5) QOTLBO | {18,61,63} | {0,5334,1,1986,0,5672} | 71,6345 | {0,5310,1,4808,0,3004} | 71,5090 |
| (6) HTLBOGWO | {18,61,62} | {0,5330,1,0000,0,7730} | 71,7281 | {0,5310,1,4617,0,3196} | 71,5898 |
| (7) GA-IWD | {20,61,64} | {0,9115,1,3926,0,8059} | 80,9100 | {0,5027,1,4953,0,2898} | 71,4060 |
| (8) AHA | {12,21,61} | {0,4710,0,3120,1,6890} | 69,6669 | {0,4953,0,3125,1,7353} | 69,5677 |
| (9) KHA | {12,22,61} | {0,4962,0,3113,1,7354} | 69,5730 | {0,4960,0,3118,1,7353} | 69,5730 |
| (10) MSSA | {11,18,61} | {0,5260,0,3800,1,7180} | 69,4077 | {0,5269,0,3801,1,7189} | 69,4077 |
| (11) CHVSA | {11,17,61} | {0,5284,0,3794,1,7186} | 69,4088 | {0,5267,0,3802,1,7189} | 69,4088 |
| (12) GAMS | {12,61,64} | {0,8131,1,4447,0,2896} | 72,7900 | {0,8137,1,4446,0,2897} | 71,9504 |
| (13) CBGA-VSA | {11,18,61} | {0,5268,0,3801,1,7190} | 69,4077 | {0,5269,0,3801,1,7189} | 69,4077 |
Source: Authors
The numerical results reported in Table 7 allow concluding that:
Only two out of the thirteen methods find the global optimal solution of the OPF problem in the 69-node test feeder, i.e., 69,4077 kW. These methods are the MSSA and the CBGA-VSA, and their DGs are located at nodes 11, 18, and 61. The SOCP approach finds the same solution as these methods, albeit with small variations in the power injected. This behavior is attributable to the multimodal behavior of the OPF problem in distribution networks.
For the remaining 11 methods, when the power losses are compared, it is possible to observe that the SOCP has the best numerical performance in all the cases. The highest difference occurs in the case of the GA-PSO with 15,1832 kW, followed by the GA-IWD with 9,5040 kW. These results confirm that some combinatorial methods are stuck in locally optimal solutions, which can be attributable to the parametrization of these algorithms, as they can be sensitive to the number of iterations, population size, or evolution criteria.
In general, the results in Table 7 confirm that the SOCP approach is more reliable for solving the OPF problem in distribution networks since, mathematically speaking, the global optimal solution is ensured, which is not possible for metaheuristic optimization methods. To demonstrate this, in the following section, simulations with the VSA are performed with a statistical focus, and the results are compared to those of the SOCP approach. This method was selected because it is the most efficient technique that has recently been reported in the literature on OPF analysis, which is due to its use of Gaussian distributions to explore and exploit the solution space (Montoya et al., 2019).
6.4. RESULTS OBTAINED BY THE 69-NODE TEST FEEDER
For the 69-node network, the same considerations were taken into account, namely the number of individuals, the number of iterations, and the number of algorithm executions.
Figures 6 and 7 present the results obtained for the global optimum or objective function, as well as the processing times for each of the methods implemented in the 69-node network.
The optimal DG sizes obtained, along with the best solution for each method, are presented in Table 8.
Table 8 DG optimal size for each node in the 69-node test feeder
| Method | Node 11 (kW) | Node 18 (kW) | Node 61 (kW) |
|---|---|---|---|
| PSO | 528,08899 | 379,29616 | 1.718,89968 |
| CSA | 523,71161 | 393,93201 | 1.710,80861 |
| AG | 526,89844 | 379,90107 | 1.718,74978 |
| BH | 526,85060 | 380,69604 | 1.719,15175 |
| SCA | 521,04921 | 383,20855 | 1.719,49453 |
| VSA | 526,32031 | 371,46626 | 1.713,36345 |
| SOCP | 522,35421 | 374,53354 | 1.714,23456 |
Source: Authors
The statistical values obtained for the maximum value and the standard deviation are presented in Table 9, and the averages of the problem’s relevant variables for the 69-node system are presented in Table 10.
Table 9 Maximum and standard deviation in the 69-node test feeder regarding the objective function value
| Method | Higher value Ploss (kW) | Standard deviation (kW) |
|---|---|---|
| PSO | 74,47234549 | 0,89754997 |
| CSA | 72,69016241 | 0,685864371 |
| AG | 69,56054542 | 0,000523881 |
| BH | 69,56852805 | 0,002519536 |
| SCA | 69,69261281 | 0,021846751 |
| VSA | 70,13257921 | 0,111839301 |
Source: Authors
Table 10 Average of the problem’s interest variables in the 69-node test feeder
| Method | Node 11 (kW) | Node 18 (kW) | Node 61 (kW) | Ploss (kW) | Proc. time (s) |
|---|---|---|---|---|---|
| PSO | 550,8664245 | 410,6438291 | 1.640,970481 | 70,17983654 | 7,126776063 |
| CSA | 459,3787818 | 369,3868411 | 1.748,294781 | 70,61552772 | 6,727355188 |
| AG | 526,6663213 | 379,6927151 | 1.719,216721 | 69,55627009 | 6,742606877 |
| BH | 532,2441399 | 380,8071298 | 1.715,379311 | 69,55852607 | 6,800026994 |
| SCA | 520,1028272 | 380,6536084 | 1.719,012024 | 69,56088641 | 8,122573602 |
| VSA | 512,8563583 | 385,5910131 | 1.723,311221 | 69,72104881 | 7,431164393 |
Source: Authors
The results obtained in the validation show that:
As in the 33-node system, the SOCP obtained the best results regarding the objective function. A much lower processing time was observed in comparison with the other metaheuristic methods, which is due to the linear or exact nature of SOCP, as it does not require iteration to find the best solution.
With the metaheuristic methods, the GA algorithm, with 69,555992 kW, was the one with the least losses -less than the exact SOCP method. This shows that metaheuristic methods are very efficient and can reach better answers than exact techniques.
The GA yields better results regarding loss reduction when compared to the SOCP method. It also has a longer processing time -almost four times longer than the SOCP. This allows the user to choose which one would be better when dealing with an optimization problem.
The CSA method is the one with the greatest deficiency in the reduction of power losses, with results of 69,564495 kW, and its standard deviation is one of the highest. However, its results are in a range close to the general results obtained with the different methodologies.
The GA algorithm has the lowest standard deviation, which makes it the most accurate metaheuristic algorithm, unlike the PSO, which is the algorithm with the highest standard deviation -and therefore the most inaccurate- within the evaluation environment defined in this work.
It should be noted that the GA is the algorithm that requires the highest number of iterations (1.000) in order to obtain an optimal result. Nevertheless, its processing times are low due to its nature, which only requires simple operations, comparisons, and replacements.
For the 69-node system, the node that requires the most power regarding DG is node 30, with a power of approximately 1.719 kW, followed by node 13, with about 527 kW, and node 24, with approximately 385 kW. These results were compared to those reported in the specialized literature, with the same sizing values for the selected DG locations.
The standard deviation values presented in Table 9 show that the results were as expected: in both 33- and 69-node systems, it was demonstrated that the methods are highly accurate, which is due to their low standard deviation.
The averages of the DG sizing value, objective function, and processing time shown in Table 10 are low, with a high similarity to the optimum of each method.
It can be concluded that the results are good with regard to the penetration of DGs in electrical networks and their implementation with metaheuristic and exact methodologies. There is a 69% reduction in the total system losses, going from 225,0718 to about 69,556 kW.
6.5. Additional results
In order to observe the direct impact of DG in each of the implemented grids, an additional analysis is presented, which is a verification of the nodal voltage profiles, as this is an indicator of the efficiency and operation of the grid, and it evidences the regulatory compliance of electrical systems. To demonstrate the improvement of this parameter in the networks, the profiles of the original system were obtained, as well as the profiles of the network subjected to the penetration of DG.
The results obtained for the 33-node network are shown in Figure 8.
The results obtained for the 69-node network are shown in Figure 9.
The results reported in Figures 8 and 9 confirm that DG improves the voltage profiles in the two networks, achieving more uniform results in each of the system nodes, which ensures greater efficiency for the network. Before the penetration of DG in the 33-node network, values oscillated between 0,91 and 1,00 p.u., and most of the nodes had values equal to or lower than 0,95 p.u. The integration of DG yielded a homogeneous behavior, with oscillations between 0,983 and 1 p.u. Furthermore, in the 69-node network, the voltage profile values at the different nodes initially oscillated between 0,91 and 1.00 p.u. With the integration of DG, the oscillation range improved, i.e., between 0,992 and 1,00 p.u.
7. CONCLUSIONS AND FUTURE WORK
This paper presented a complete comparison between metaheuristic optimization methods and the SOCP approach for solving the OPF problem in AC distribution networks. The exact nonlinear model of the OPF problem and its conic relaxation were presented in order to show the main complications of its solution. Computational validations showed that the metaheuristic approaches manage to obtain very good results that are directly comparable to those of the SOCP. Actually, the reported validations show a great performance of the GA for the two test systems, which makes it the best methodology used in this study. In general, the range of oscillation of the results obtained with the studied methodologies shows that the difference between the best and the worst global optimum is about 10 W. Based on this value, a satisfactory comparison between metaheuristic and convex optimization is clearly achieved, despite the problems with the iterative processes and the definition of the corresponding parameters for the metaheuristic techniques. This study shows how these techniques adequately fit the OPF problem, showing even better solutions than traditional convex optimization.
The daily problems faced by engineers and other professionals are usually of a high complexity, given the amount of data and possible solutions that a problem may have. With this in mind, combinatorial solutions (metaheuristic methods) allow finding acceptable solutions with reasonable computation times by applying the knowledge obtained while observing nature. Metaheuristic techniques bring innovative ideas because they are not rigid algorithms, which makes them very versatile methods that can be adapted to any combinatorial optimization problem software. The task of determining the initial variables of the algorithms is part of the programmer’s criterion, leading to an infinite number of possible programs that address the same problem, all focused on finding the best solution to the objective problem in the shortest possible time. As seen in this paper, DG depends on many variables such as its topology, the number of generators, and their position, size, and cost. A programmer’s task is to carefully establish the criteria for the selection of the generators, as the quality of the solutions to be found depends on it. Metaheuristic methods can be implemented in various computational tools and adapted to them, thus demonstrating that large programs or licenses are not required to find an acceptable solution to combinatorial optimization problems.
As future work, the following research could be conducted: i) comparing metaheuristics against SOCP programming in optimization problems that include binary variables, such as the optimal location of capacitor banks or the optimal location of DGs in electrical distribution networks, and ii) comparing both approaches in economic-environmental applications in transmission power systems with a high penetration of renewable energy and battery energy storage systems.