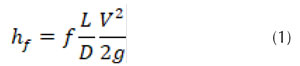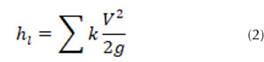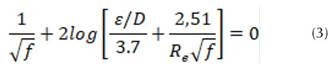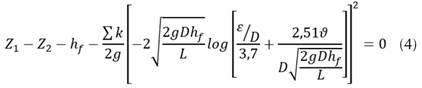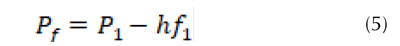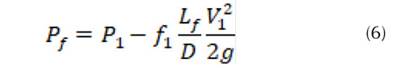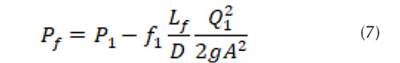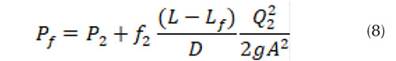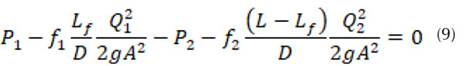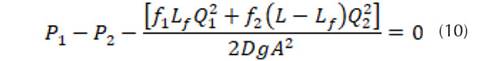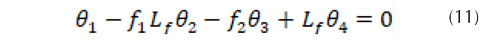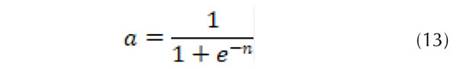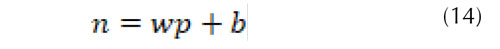Introducción
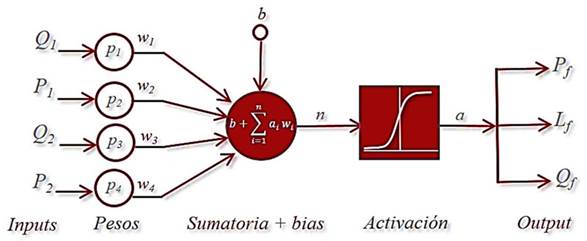
Las detecciones de fugas en tuberías pueden ser abordadas desde dos enfoques: uno basado en hardware (monitoreo) y otro centrado en el software (Lu et al., 2020). La complejidad de los sistemas hidráulicos y especialmente en lo referente a la localización y cuantificación de las fugas en sistemas de acueducto radica en la no linealidad de las ecuaciones diferenciales que gobiernan el flujo a presión. La localización de fugas, la estimación de presiones y los caudales generados por la pérdida de agua constituyen un problema Np-Duro, es decir, no existe un método determinístico que resuelva el problema en un tiempo polinomial establecido y con un costo computacional aceptable. Así, las ecuaciones de flujo a resolver corresponden a la ecuación de conservación de masa en el nodo donde se presenta la fuga y las ecuaciones de conservación de energía. La determinación de la cantidad de masa y la posición de una fuga para un sistema hidráulico simple en el cual la sección transversal de la tubería permanece constante dependen directamente del comportamiento del gradiente hidráulico (Figura 1). Al generarse la fuga se evidencia un cambio de velocidad dentro del sistema, por lo cual se establece una mínima variación en el coeficiente de fricción antes y después de la fuga. Si se considera la existencia de varias fugas en el sistema hidráulico conformado por diferentes mallas o bucles se estructura un problema hidráulico de alta complejidad, debido a la sensibilidad de las variables de entrada. Este problema puede ser abordado desde el campo de la inteligencia artificial a partir de algoritmos híbridos de clasificación, cuyo objetivo es reducir el área donde se generan las fugas en el sector hidráulico. La arquitectura de red neuronal parte de las variables de entrada como son las presiones y los caudales de entrada y salida. Estos valores son afectados por los pesos sinópticos y pasan a través de la función de activación, este proceso se repite en forma de bucle hasta alcanzar la capacidad de generalización de la estructura neuronal. El desarrollo de redes neuronales implementados en sistemas hidráulicos ha demostrado alta eficiencia en términos de variables de salida (Burton et al., 1999). Si bien es cierto que existen otros tipos de metaheurísticas para la detección de fugas como máquinas de soporte vectorial, algoritmos genéticos, lógica difusa y esquemas meméticos, las redes neuronales, debido a su capacidad de aprendizaje, presentan resultados óptimos con respecto a la cuantificación y la localización de fugas en los sistemas de distribución de agua potable y transporte de hidrocarburos, entre otros, por lo cual se puede afirmar que las redes neuronales han demostrado resultados robustos para problemas de alta complejidad (Caputo y Pelagagge, 2003).
Metodología
Hidráulica de la fuga
Para un sistema hidráulico con una única fuga es posible determinar la cantidad de masa y la localización de la fuga mediante la igualación de la pérdida de carga antes y después de la fuga. Al aceptar la ecuación que gobierna el comportamiento del flujo a presión dada por (1) se establece un sistema subdeterminado debido a la existencia de más incógnitas que ecuaciones (9). Esto puede ser resuelto a través de un bucle anidado para el cálculo de los coeficientes de fricción y la posición lineal de la fuga. Para un sistema presurizado la pérdida por fricción está dada por la ecuación de Darcy-Weisbach.
Donde, : pérdida de carga (m); : coeficiente de fricción; : longitud tubería (m); : diámetro (m); : velocidad media del flujo (m/s); : gravedad (m/s2). Para las pérdidas menores o por accesorios, se tiene,
Donde, : pérdidas menores (m); : coeficiente de pérdidas menores (adimensional); : velocidad media del fluido (m/s); : aceleración de la gravedad (m/s2). Para el cálculo del coeficiente de fricción (f) se implementó la ecuación propuesta por Colebrook-White (3).
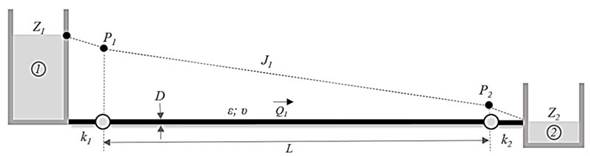
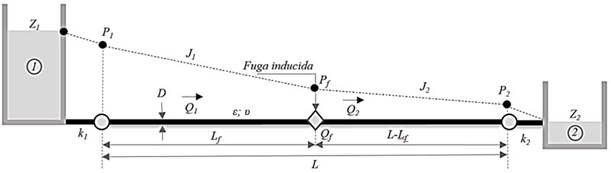
Donde, f: coeficiente de fricción; : rugosidad del tubo (m), D: diámetro (m); R e : número de Reynolds. La presión para el punto de la fuga (P f ) está dada por la diferencia entre la presión inicial (P 1 ) y las pérdidas por fricción antes de la fuga (hf 1 ) (Figura 2). Aceptando la ecuación de Darcy-Weisbach (1) se obtiene la pérdida de carga en el tramo antes de la fuga, donde el coeficiente de fricción se determina de forma iterativa implementado el modelo propuesto por Colebrook-White (3). La Figura 1 presenta el esquema hidráulico para una tubería principal sin derivaciones en la cual no se evidencia la presencia de fugas en el sistema. La diferencia de nivel entre los tanques establece la pérdida de carga total del sistema (H). El modelo hidráulico presenta dos accesorios (k 1 , k 2 ) a la entrada y a la salida del sistema respectivamente. De igual forma, el diámetro permanece constante a lo largo de la longitud de la tubería. Conociendo el diámetro, la pérdida de carga, la rugosidad, la longitud del tubo, la viscosidad y la sumatoria producida por los accesorios es posible determinar el caudal a partir de la ecuación (4). Esta ecuación resuelve la mayoría de problemas de tuberías simples, debido a que la única incógnita corresponde a la pérdida por fricción (h f ).
La solución para h f se puede obtener a partir de la herramienta análisis de hipótesis (Excel®), donde la función objetivo corresponde a la ecuación (4). Esta ecuación resuelve un sistema hidráulico para tuberías conectadas por una sola tubería con un solo diámetro y diferentes accesorios, estableciendo un depósito al inicio y al final del sistema. El comportamiento de la línea de gradiente hidráulico para un sistema de tuberías simple está dado por la Figura 1.
La suma de la elevación con respeto a un datum y la altura de presión corresponden a la línea de gradiente hidráulico (LGH), esta línea indica la presión en términos de columna de agua a lo largo de la tubería. Por encima de la LGH y paralela a esta se establece la línea de energía (LE) separada por la altura de velocidad (V2/2g).
Una vez se genera la fuga (Figura 2), se origina un cambio significativo del gradiente hidráulico () (Gupta, Kishore y Jain, 2017). Las presiones (P 1 , P 2 ) cambian con respecto a las presiones determinadas por el sistema sin fuga. Rojas, Verde y Torres (2021) proponen un polinomio de segundo orden para modelar el gradiente hidráulico () a partir de diferentes rangos de velocidades. En consecuencia, la ley de potencia N1, una versión aproximada del concepto FAVAD (Fixed And Variable Area Discharges) se ha utilizado desde 1994 para la evaluación de fugas en concordancia con el concepto simplificado de Factor Noche-Día (NDF) (Lambert, Fantozzi y Shepherd, 2017). Al presentarse un cambio de velocidades en el sistema debido a la aparición de la fuga se establecen tres incógnitas a determinar: el coeficiente de fricción antes de la fuga (f 1 ); la localización longitudinal de la fuga (L f ) y el coeficiente de fricción después de la fuga (f 2 ), resuelto esto es posible cuantificar la cantidad de masa y la presión en el punto de la fuga. Es decir, teniendo en cuenta los vectores de entrada netos (Q 1 , Q 2 , P 1 , P 2 ) es viable obtener una solución para la ubicación de la fuga, el caudal y la presión en ese punto (Q f , P f , L f ) a partir de la ecuación (11).
La ecuación parametrizada está dada por (12), estableciendo tres incógnitas (), las cuales pueden ser encontradas a partir de las condiciones hidráulicas de entrada y la ejecución iterativa de un bucle anidado.
Al igualar la presión antes () y después de la fuga (), se tiene:
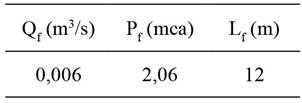
Para establecer la capacidad del algoritmo (11), se propone una tubería de 30 m que conduce agua con una viscosidad cinemática de 0,000001 (m2/s), un diámetro igual a 0,15222 m y con una rugosidad de 0,0000015 m. Se instalaron en el sistema hidráulico dos caudalímetros y dos manómetros virtuales al inicio y al final de la tubería, las lecturas obtenidas aparecen en la Tabla I.
La Tabla II muestra el proceso iterativo realizado, se estableció la función objetivo (FO_f1) para el coeficiente de fricción antes de la fuga a partir de Colebrook-White (3). De igual forma, se obtuvo el coeficiente de fricción después de la fuga (f 2 ). Finalmente, la función objetivo está dada por (FO_Lf) donde el objetivo es minimizar la ecuación (11) modificando la localización de la fuga a lo largo de la tubería partiendo del tanque 1 (L f ). Es decir, encontrar el valor de L f que minimice (11).
Implementado Visual Basic (Excel®) se realiza un bucle anidado para la función objetivo (11).
Sub Fuga()
For i = 1 To 6
Range("G12").Select
Do Until ActiveCell = ""
ActiveCell.Offset(0, 1).GoalSeek Goal:=0, ChangingCell:=ActiveCell
ActiveCell.Offset(1, 0).Range("A1").Select
Loop
Range("K12").Select
Do Until ActiveCell = ""
ActiveCell.Offset(0, 1).GoalSeek Goal:=0, ChangingCell:=ActiveCell
ActiveCell.Offset(1, 0).Range("A1").Select
Loop
Range("M12").Select
Do Until ActiveCell = ""
ActiveCell.Offset(0, 1).GoalSeek Goal:=0, ChangingCell:=ActiveCell
ActiveCell.Offset(1, 0).Range("A1").Select
Loop
Next i
End Sub
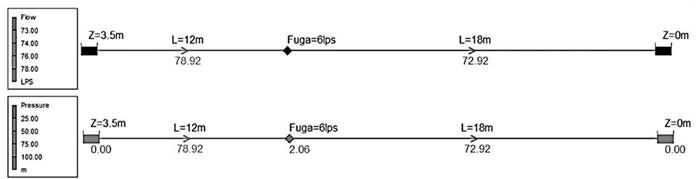
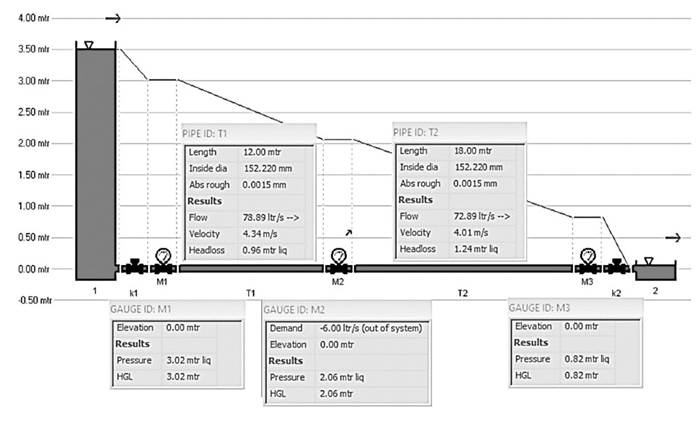
La solución encontrada a partir de las condiciones de frontera preestablecidas y la función objetivo (11), indican que el sistema presentará una fuga a 12 m medidos desde el tanque 1 (Figura 2). La fuga presenta un caudal de 6 lps y una presión manométrica en ese punto igual a 2,06 mca.
La validación de estos resultados se realizó a través del software Epanet® desarrollado por la Agencia de Protección Ambiental de Estados Unidos, este software es utilizado para modelar y diseñar sistemas a presión, de igual forma, es posible realizar el seguimiento de sustancias en la red, también es viable para la detección de fugas a partir de emisores (Mashford et al., 2009). Epanet® resuelve diferentes ecuaciones no lineales simultáneamente utilizando métodos iterativos con el objetivo de alcanzar el equilibrio de red (Jasper et al., 2013). Si la red no presenta fuga el valor del coeficiente del emisor será igual a cero. El caudal generado por el emisor es igual al producto del coeficiente del emisor y la presión en el nodo elevada a una potencia. La potencia recomendada es 0,5, que normalmente se aplica a rociadores y boquillas.
Donde, caudal en la fuga (m3/s); presión en el nodo (mca); coeficiente del emisor; potencia. En el caso de las condiciones establecidas en la Tabla I, el caudal generado por la fuga está dado por:
Bajo esta consideración el coeficiente del emisor utilizado en Epanet® corresponde a 4,18, el cual garantiza un caudal en la fuga de 6 lps. La simulación hidráulica se realizó bajo condiciones estacionarias del flujo con una pérdida de carga de 3,5 m, longitud de la tubería igual a 30 m, un accesorio a la entrada con k1 igual a 0,5 y uno a la salida con k2 igual a 1.
De igual forma, a partir del software Hydroflo® (Tahoe Design Software) se modeló el tramo de tubería colocando tres manómetros, uno a la entrada (M1) y a la salida (M2) de la tubería, y otro en la ubicación de la fuga inducida (M3), los resultados obtenidos se presentan en la Figura 4.
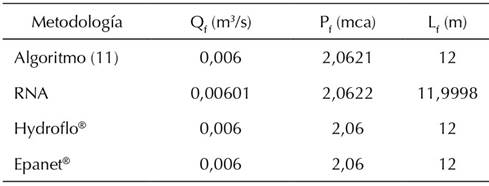
La Tabla IV muestra la comparación entre las cuatro metodologías con base en los datos de entrada (Tabla I). De igual forma, se validaron 45 sistemas hidráulicos independientes bajo las mismas condiciones hidráulicas de entrada (pérdida de carga, diámetro, rugosidad y longitud del tubo), modificando la posición (L f ) y el caudal de la fuga (Q f ). Los resultados obtenidos con la ecuación (11) presentan una aproximación a la décima de milímetro con respecto a la posición virtual de la fuga obtenida en los modelos simulados y una aproximación a la décima de litro con respecto al caudal generado por la fuga. Una vez validado el algoritmo se construyó el conjunto de datos de entrenamiento para la RNA (red neuronal artificial).
Procesamiento de datos
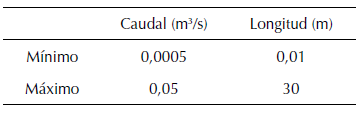
Los datos se establecieron a partir de la función objetivo dada por (11) con base en un algoritmo anidado realizado en Visual Basic (Excel®), para lo cual se determinó el caudal generado por la fuga (Q f ), la presión manométrica en la fuga (P f ) y la posición longitudinal (L f ) para 35.837 escenarios diferentes. Estos datos de entrada se generaron de manera aleatoria y se ajustan a la distribución normal para el caudal al inicial del tramo (Q 1 ), presión manométrica inicial (P 1 ), caudal al final del tramo (Q 2 ), presión manométrica al final de la tubería (P 2 ). Los datos están disponibles en el siguiente enlace (descarga datos). El Dominio de las variables de entrada se muestran en la Tabla V.
Arquitectura de la red neuronal artificial (RNA)
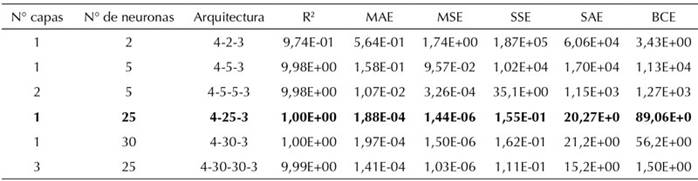
Para definir la estructura de una red adecuada es necesario determinar el número de neuronas ocultas. De hecho, para describir relaciones complejas no lineales, aumentar la cantidad de neuronas y capas ocultas puede mejorar la capacidad de la RNA (Fan, Zhang y Yu, 2021). Esta cantidad afecta de manera significativa el potencial de rendimiento de la red (Bishop, 2005). La Tabla VI presenta seis arquitecturas diferentes para abordar el cálculo de la fuga y la localización en una tubería principal sin ramificaciones en términos de un modelo estacionario. Es posible realizar simulaciones sintéticas transitorias a partir del cierre de una válvula utilizando una simulación numérica (Bohórquez et al., 2020). Sabu et al. (2021) proponen un modelo inteligente para el mapeo de varios nodos de fuga en función de los valores de presión con una precisión significativa. Para este estudio el esquema que presentó mejores resultados con base en el MSE y el estadístico R correspondió a la arquitectura con cuatro variables de entrada, una capa oculta con 25 neuronas y tres variables de salida [4-25-3], esto bajo tiempos computacionales aceptables.
La Tabla VI muestra cómo el número de neuronas y la cantidad de capas ocultas inciden sobre el MSE y el R2, además la precisión del modelo determinado depende del número de neuronas en el nivel topológico (Rojek y Studzinski, 2019). No obstante, este estudio evidenció que al aumentar el número de neuronas y de capas ocultas el MSE se estabiliza en valores cercanos a 1,03E-06. Esto indica que al aumentar el número de neuronas o de capas ocultas el estadístico MSE no va a mejorar y se comporta de forma asintótica con respecto al número de épocas (Figura 7a). De hecho, los tiempos computacionales aumentan considerablemente. Por ejemplo, para alcanzar convergencia en la arquitectura [4-30-30-3] se requieren 3 horas y 32 minutos de procesamiento computacional.
La Tabla VI presenta diferentes arquitecturas neuronales para la optimización de la ubicación de la fuga.
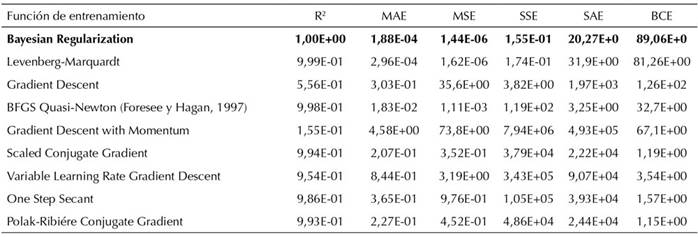
Entrenamiento de la red neuronal
El desarrollo de la RNA requiere tres etapas bien definidas: la arquitectura de la red, las funciones de activación y el algoritmo de aprendizaje (Simpson, 1991). En el proceso de entrenamiento se considera aleatorios a los pesos iniciales, una vez se ha producido la primera época, estos valores cambian y se ajustan de forma continua. Para este estudio los pesos se optimizaron con el algoritmo de regularización bayesiana teniendo en cuenta el MSE y el coeficiente de determinación R 2 , el cual explica la variación de las variables respuesta (Q f , P f , L f ) explicadas por las variables independientes (Q 1 , Q 2 , P 1 , P 2 ) (Tabla VII). Se utilizó MatLab (2021a) para analizar los algoritmos de aprendizaje de retropropagación y regularización bayesiana. La RNA se entrena dividiendo en tres conjuntos los datos de entrada a partir de índices aleatorios, esto para validar la predicción de la posición, la presión y el caudal en la fuga. De igual forma, la función de transferencia log sigmoide “logsig” presentó los mejores resultados y los mínimos estadísticos, esto se evidencia en la Tabla VIII, donde la función de transferencia calcula la salida de la capa oculta a partir del vector de entradas netas.
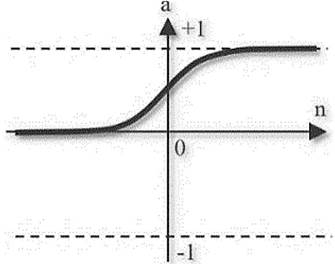
La función de activación log sigmoide “logsig” está definida por la siguiente expresión,
Donde está definido como el vector que contiene los pesos sinápticos (w) multiplicados por los patrones (p) de entrada más un valor del sesgo de la red (b); corresponde a las señales de salida (Q f , P f , L f ).
La función de transferencia log sigmoide “logsig” se implementó para la red multicapa entrenada a partir del algoritmo de retropropagación, esto debido a que esta función es diferenciable.
La Figura 7a presenta el rendimiento de la red graficando el MSE con respecto a la época para la etapa de entrenamiento, la validación y los rendimientos de prueba de los datos de entrenamiento. Durante una época, la función de pérdida se calcula para todos los datos estableciendo el valor de la pérdida cuantitativa en la época determinada. Lo recomendable para estas tres funciones es que adopten una tendencia similar de forma descendente. Dado el caso en el cual las gráficas de las funciones comiencen a alejarse una de otra, el modelo estará sobre-entrenado, afectando su capacidad de generalización.
Al aumentar el número de épocas la función de control se reduce. Sin embargo, para este estudio el MSE comenzó a comportarse de forma asintótica después de las 6.000 épocas, tomando el error de validación el MSE más bajo. La Figura 7b presenta la variación del coeficiente del gradiente con respecto al número de épocas. El valor final del coeficiente del gradiente para la época 6.000 es 3,179E-05, que es aproximadamente cercano a cero.
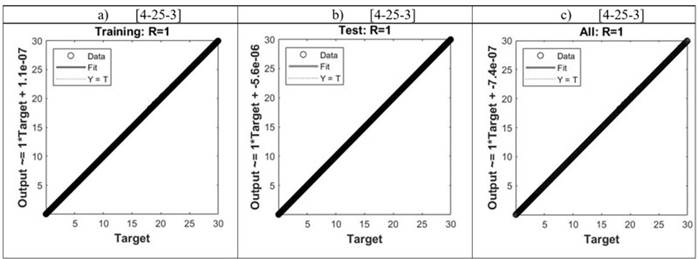
Debido a que a MatLab R2021a divide el conjunto de datos de forma aleatoria, se origina la Figura 8, esta indica la relación lineal que existe entre los valores objetivo de los datos de entrenamiento y los valores estimados por la red neuronal. Si la entrada es igual a la respuesta se formará una recta a 45° con respecto a la horizontal, indicando que el valor del coeficiente de determinación es igual a 1. La Figura 8a establece la correlación lineal para los datos de entrenamiento, mientras que la Figura 8b indica la correlación lineal para el conjunto de datos de prueba seleccionados aleatoriamente por MatLab R2021a a partir de la función “dividerand” (división del conjunto de datos objetivo en tres conjuntos utilizando índices aleatorios).
Resultados
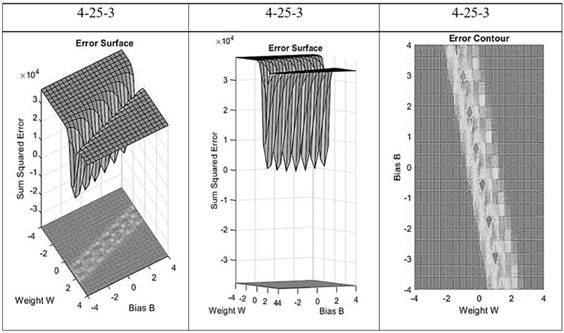
Este estudio implementó el método de propagación hacia atrás “backpropagation”, en el cual se establece un patrón en la entrada de la red afectado por los pesos sinópticos y el sesgo, estos valores son transferidos a la función log sigmoide originando las señales de respuesta. Al comparar estas señales de salida con los valores de entrenamiento se genera una matriz de errores en el que el objetivo del método es minimizar la magnitud de la superficie de error (Figura 9).
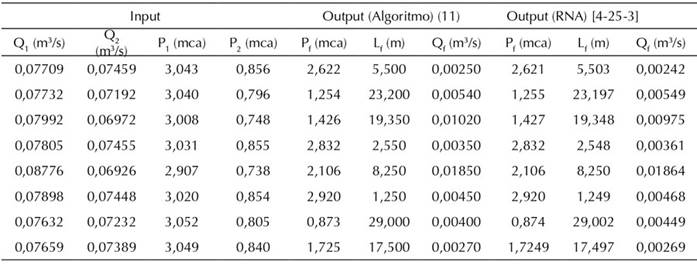
La Tabla IX presenta de forma explícita el cálculo de la presión, el caudal y la posición de la fuga para ocho escenarios diferentes, comparando los resultados obtenidos con el algoritmo (11) y los valores estimados por la RNA [4-25-3].
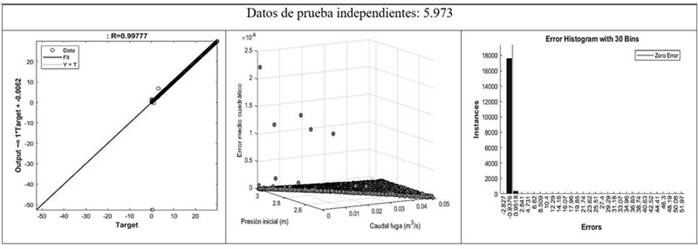
La capacidad de estimación de una RNA se mide a partir del potencial de generalización. Es decir, la capacidad que tiene la red para estimar el vector respuesta a partir de un conjunto de datos nuevos, datos que la red no conocía y con los cuales no ha sido entrenada. Para este estudio se estableció un conjunto de 5.973 datos de prueba con el objetivo de realizar el proceso de validación cruzada. La Figura 10 ilustra el comportamiento estadístico de la serie de entrenamiento. Como función de control se implementó el MSE obteniendo un valor de 0,995. Los estadísticos obtenidos a partir del conjunto de datos de prueba se presentan en la Tabla X demostrando la capacidad de generalización de la RNA [4-25-3].
El histograma de error mostrado en la Figura 10 indica la forma como se distribuyen los tamaños de error. Por lo cual, la mayoría de los errores para los datos de prueba independientes están cerca de -0,9376.
Conclusiones
El objetivo de este trabajo fue comprobar la capacidad de las redes neuronales para predecir el comportamiento de una fuga en una tubería principal. Los resultados obtenidos demuestran el potencial de la inteligencia artificial aplicado a la detección de fugas. Este estudio demostró que es posible localizar, cuantificar y establecer el nivel de presión de una posible fuga para cualquier sistema de tubería principal sin ramificaciones, a partir de la consolidación de un conjunto de datos de entrenamiento calculados con base en el algoritmo (11). La estructura neuronal corresponde a un vector de entrada con cuatro variables, una capa oculta con 25 neuronas y tres variables de salida [4-25-3] (Figura 5).
Se evidenció que al aumentar el número de neuronas y de capas ocultas el MSE se estabiliza en valores cercanos a 1,03E-06. Esto indica que al incrementar el número de neuronas o de capas ocultas el estadístico MSE no va a mejorar y se comporta de forma asintótica con respecto al número de épocas. La capacidad de generalización de la red neuronal se demuestra a partir de los estadísticos obtenidos en el proceso de validación cruzada de los 5.973 datos de prueba independientes. Finalmente, la red neuronal tiene la capacidad de localizar la fuga a partir del caudal inicial, el caudal final, la presión inicial y la presión final obtenidos por los sensores virtuales ubicados en el sistema hidráulico.