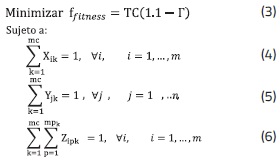MÉTODOS DISCRETOS BASADOS EN QUIMIOTAXIS DE BACTERIAS Y ALGORITMOS GENÉTICOS PARA SOLUCIONAR EL PROBLEMA DE LA DISTRIBUCIÓN DE PLANTA EN CELDAS DE MANUFACTURA

DISCRETE METHODS BASED ON BACTERIAL CHEMOTAXIS AND GENETIC ALGORITHMS TO SOLVE THE CELL MANUFACTURING LAYOUT PROBLEM

Camilo Mejía Moncayo¹, Diego Alexander Garzón Alvarado², José Manuel Arroyo Osorio³

¹ Ing. Mecánico, MSc. Profesor Asistente, cmejiam@correo.ean.edu.co, cmejiamo@unal.edu.co Programa de Ingeniería de Producción, Universidad EAN, Bogotá, Colombia.
²Ing. Mecánico, Ph.D. Profesor Titular, dagarzona@unal.edu.co, Departamento de Ing. Mecánica y Mecatrónica, Universidad Nacional de Colombia, Bogotá, Colombia.
³ Ing. Mecánico, Ph.D. Profesor Asociado, marroyoo@unal.edu.co, Departamento de Ing. Mecánica y Mecatrónica, Universidad Nacional de Colombia, Bogotá, Colombia.

Referencia: C. Mejía Moncayo, D.A. Garzón Alvarado, J.M. Arroyo Osorio. (2014). Métodos discretos basados en quimiotaxis de bacterias y algoritmos genéticos para solucionar el problema de la distribución de planta en celdas de manufactura. Ciencia e Ingeniería Neogranadina, 24 (1), pp. 6-28.

Fecha de recepción: 7 de febrero de 2013 Fecha de aprobación: 10 de abril de 2014

RESUMEN

Este trabajo presenta la solución mono-objetivo y multi-objetivo del problema de la distribución de planta en celdas de manufactura a través de dos nuevos algoritmos híbridos discretos basados en quimiotaxis de bacterias y en algoritmos genéticos. Los modelos propuestos resuelven simultáneamente los dos inconvenientes que constituyen el problema de la distribución de planta en celdas de manufactura: la formación de las celdas y la distribución de planta intra e inter celdas, considerando el agrupamiento de las celdas y el costo de transporte y manipulación de materiales. El desempeño de las propuestas se evaluó con problemas de prueba de distribución de planta de celdas de manufactura, agente viajero (TSP) y el caso multi-objetivo del problema de las mochilas. Los resultados mono-objetivo se compararon con AG, BFOA y Bacterial-GA, mientras que los resultados multi-objetivo se compararon con los reconocidos algoritmos NSGA2 y SPEA2 en los que se obtuvo un mejor desempeño en los dos casos.

Palabras clave: distribución de planta de celdas de manufactura, optimización, algoritmos genéticos, BFOA, NSGA2, SPEA2, BCMOA, hibridación.

ABSTRACT

This paper presents the mono-objective and multi-objective solution to the cell manufacturing layout problem using two new discrete hybrid algorithms based on bacterial chemotaxis and genetic algorithms. The proposed models simultaneously solve the issues that constitute the problem of the layout of manufacturing cells: the formation of the cells and the inter- and intra-cell layout, considering the clustering of cells, and the cost of transportation and material handling. The performance of the proposals was evaluated with benchmark problems of manufacturing cells, traveling salesman problem and a multi-objective version of knapsack problem. The mono-objective results were compared with GA, BFOA and Bacterial-GA, while the multi-objective results were compared with well-known algorithms NSGA2 and SPEA2, obtaining better performances in both cases.

Keywords: cell manufacturing layout, optimization, genetic algorithms, BFOA, NSGA2, SPEA2, BCMOA, hybridization.

INTRODUCCIÓN

Las celdas de manufactura son unidades funcionales de organización de la producción basadas en la filosofía de tecnología de grupos [1]. La formación de las celdas se basa en la agrupación de partes y máquinas a partir de las similitudes entre estas. Las celdas de manufactura pueden asimilarse a pequeñas minifábricas al interior de la planta donde se fabrican un grupo de piezas similares, llamado familia de partes, en un conjunto de máquinas agrupadas para tal fin. Este tipo de configuración es particularmente apropiado para sistemas de manufactura con diversidad de productos y volúmenes de producción variables. Definir la distribución de planta de celdas de manufactura implica solucionar dos problemas: primero, la formación de las celdas y las familias de partes; y en segundo lugar, definir la distribución de planta intra e inter celdas. Es decir, la implementación de celdas de manufactura inicia con la formación de grupos de máquinas y familias de partes. En este proceso se agrupan las partes en familias a partir de las similitudes que tienen en sus procesos de fabricación y/o geometría y las máquinas se agrupan en celdas siguiendo las similitudes en las piezas que en ellas se fabrican.

Existen diversos métodos para formar las celdas como lo describen Selim et al. [2], quienes clasifican los procedimientos de formación de las celdas en métodos descriptivos, análisis de agrupamiento, partición gráfica, programación matemática e inteligencia artificial. Papaioannou y Wilson [3] añaden a esta clasificación los métodos con algoritmos heurísticos y meta heurísticos y, finalmente, Yin y Yasuda [4] describen y clasifican las propuestas basadas en coeficientes de similitud, que son uno de los tipos de técnicas con base en análisis de agrupamiento.

Posteriormente a la formación de las celdas de manufactura, es necesario resolver el problema de la distribución de planta intra e inter celdas de manufactura, que consiste en la asignación de las máquinas o procesos que conforman las celdas a una posición determinada dentro de ésta, la cual a su vez debe ser también asignada a una determinada posición respecto al resto de celdas. El planteamiento general se basa principalmente en la minimización del costo del transporte y el manejo de materiales, que está directamente relacionado con el sistema de manejo de materiales. Este aspecto es muy importante, ya que de él depende la forma que puede tomar la distribución de la celda al interior de ésta [5].

El problema de la distribución entre celdas puede ser planteado considerando las relaciones existentes entre las celdas, que pueden ser cuantitativas o cualitativas, como lo plantean Elwany et al. en su propuesta [6] en la cual emplean un algoritmo de mejora que trabaja en serie con un algoritmo de recocido simulado para establecer la posición de las celdas entre sí. Otra forma es plantearlo considerando los flujos de materiales entre las celdas como un problema de asignación cuadrático (QAP, Quadratic Assignment Problem) como lo presentan Solimanpur, et al. [7], quienes lo solucionan con un algoritmo ACO (Ant Colony Optimization).

La solución simultánea de la formación de las celdas de manufactura y la distribución intra e inter celdas determina la naturaleza multi-objetivo del problema. La solución puede plantearse de dos formas, la primera es llevar el problema multi-objetivo a uno mono-objetivo, al integrar en la función objetivo la formación de las celdas y la definición de la distribución de planta como lo presentan Ming y Ponnambalam [8], Ariafar et al. [9], Ho y Liao [10] y Wu et al. [11]. La segunda forma de plantear el problema es formular cada función objetivo por separado como lo presentan Solimanpur et al. [12]. La solución de la distribución de planta de celdas de manufactura se ha abordado empleando diferentes métodos como programación lineal [10], recocido simulado [9], algoritmos genéticos en versiones mono-objetivo [11] y multi-objetivo [12] y métodos híbridos como el PSO-GA [8].

En este artículo se presenta una aproximación original a la solución mono-objetivo y multi-objetivo simultánea del problema de la formación de las celdas de manufactura y la distribución de planta intra e inter celdas, empleando dos algoritmos híbridos discretos inspirados en quimiotaxis de bacterias y algoritmos genéticos. Primero, se explican los modelos matemáticos planteados y, posteriormente, los algoritmos propuestos, para terminar con los resultados de la evaluación del desempeño de estos algoritmos en la solución de tres tipos de problemas de prueba: distribución de planta de celdas de manufactura, agente viajero (TSP) y problemas multi-objetivo de mochilas.

1. METODOLOGÍA

1.1. MODELOS MATEMÁTICOS

El problema de la distribución de planta de las celdas de manufactura tiene una naturaleza multi-objetivo debido a que debe solucionar simultáneamente los problemas de la formación de las celdas de manufactura y de la distribución intra e inter celdas. A continuación se describe el proceso seguido para definir las funciones objetivo del modelo mono-objetivo y multi-objetivo.

1.1.1. Formación de las celdas de manufactura

Para lograr el agrupamiento de las celdas y familias de partes se emplea en este trabajo la eficacia de agrupamiento denominada como [13], su estructura simple permite guiar la búsqueda al mismo tiempo que cuantifica la calidad del agrupamiento logrado. se define de la siguiente forma:

Donde:

i = índice de las máquinas; i=1,…,m número de máquinas.

j = índice de las partes; j=1,…,n número de partes.

k = índice de las celdas; k=1,…,mc máximo número de celdas.

Y_jk = 1, si la parte j es asignada a la celda k, en otro caso es cero.

X_ik = 1, si la máquina i es asignada la celda k, en otro caso es cero.

a_ij = 1, si la parte j es procesada por la máquina i, en otro caso es cero (a_ij es la matriz de incidencia)

1.1.2 Costo del transporte y manipulación de materiales

Para determinar la distribución de planta intra e inter celdas se emplea el criterio de reducir el costo del transporte y manipulación de materiales, ya que permite evaluar el rendimiento de los flujos de materiales en la planta y relacionarlos con otros factores del sistema de manufactura como:

• Volúmenes de producción: estos definen el tipo y forma global de la distribución de planta.


• Cantidad de partes que se pueden transportar por movimiento: este factor afecta directamente el costo total del transporte y manipulación de materiales y debe ser tenido en cuenta en la selección del sistema de manejo de materiales.


• Secuencia de las operaciones: permite establecer la mejor posición relativa de las máquinas al interior de las celdas para evitar retrocesos y mantener flujos lineales continuos.


• Puntos de origen de la materia prima al interior de la planta y puntos de destino de las partes procesadas: influyen en la posición relativa de las celdas entre sí.

El costo de transporte (TC) depende de la distancia recorrida en cada movimiento y el tipo de movimiento que se realice. La función objetivo que se propone es la siguiente:

Donde:

i = índice de las máquinas; i=1,…,m número de máquinas

j =índice de las partes; j=1,…,n número de partes

k =índice de las celdas; k=1,…,mc máximo número de celdas

l =índice de operaciones; l=1,…,NO_j número de operaciones de la parte j

NO_j =máximo número de operaciones de la parte j

d_j,l = distancia que recorre la parte j entre la operacion l-1 y l

C_j,l = Costo del movimiento de la parte j entre la operación l-1 y l

VP_j =volumen de producción de la parte j

B_j = tamaño del lote para cada movimiento de la parte j

SM_j,l = matriz de secuencias,contiene el número de la máquina que realiza la operación l a la parte j

NCi =número de celda al que pertenece la máquina i

PCi=posición que ocupa la máquina i en la celda a la que pertenece

Dorigen_j,k = distancia de la celda k a la posición de origen del material para fabricar la parte j

Dfin_j,k = distancia de la celda k a la posición final o al siguiente proceso de la parte j

C_j,l y d_j,l pueden tomar diferentes valores dependiendo del número de la operación que se va a realizar o se realizó, como también del tipo de movimiento que realiza:

Si {l =1}Movimiento entre el punto de origen del material para fabricar la parte j y la posición de la máquina que realiza esta primera operación

1.1.3 Modelo mono-objetivo de definición de la distribución de planta de celdas de manufactura

El modelo mono-objetivo integra en una sola función objetivo la eficacia de agrupamiento (Γ) y el costo del manejo y transporte de materiales (TC). Esta propuesta contempla restricciones de unicidad que garantizan que cada máquina y parte únicamente sean asignadas a una sola celda o familia, y que a cada posición de la celda únicamente sea asignada una máquina, como se presenta a continuación:

Donde:

i = índice de las máquinas; i=1,…,m número de máquinas.

j = índice de las partes; j=1,…,n número de partes.

k = índice de las celdas; k=1,…,mc máximo número de celdas.

p = índice de las posiciones; p=1,…,mp_k máximo número de posiciones de la celda k.

X_ik =1 , si la máquina i pertenece a la celda k, en caso contrario X_ik =0

Y_jk =1, si la parte j pertenece a la celda k, en caso contrario Y_jk =0.

Z_ipk =1, si la máquina i ocupa la posición p de la celda k, en caso contrario Z_ipk =0

Para solucionar el modelo minimizando TC se resta la eficacia de agrupamiento del valor 1.1 (1.1-Γ). De esta forma se evita que se anule la función fitness cuando Γ=1 (Γ toma valores entre 0 y 1), lo cual provocaría una convergencia prematura a un mínimo para Γ pero no necesariamente para TC.

1.1.4 Modelo multi-objetivo de definición de la distribución de planta de celdas de manufactura

El modelo multi-objetivo maneja las mismas restricciones y funciones de la propuesta mono-objetivo, y minimiza la eficacia de agrupamiento (Γ) y el costo del manejo y transporte de materiales (TC) como se presenta a continuación:

1.2 ALGORITMOS PROPUESTOS

1.2.1 Discrete Hybrid Bacterial Foraging Genetic Algorithm - DHBFGA

El algoritmo DHBFGA propuesto en este trabajo es un algoritmo de optimización global que toma la idea general de la hibridación de un algoritmo genético (AG) y de un algoritmo de forrajeo de bacterias (BFOA [15]) de forma similar al algoritmo Bacterial-GA [14], que de forma general cuenta con un proceso de quimiotaxis como el BFOA [15] y el BCMOA [16]. Éste se aplica a las bacterias que pertenecen a la élite para, posteriormente y de forma análoga a un AG, realizar un proceso de selección y cruzamiento y culminar con un proceso de eliminación y dispersión típico del BFOA. El seudocódigo del algoritmo DHBFGA se presenta en la Figura 1, incluido el ciclo quimiotáctico correspondiente:

1.2.2 Discrete Hybrid - Bacterial Chemotaxis Multiobjective Optimization Algorithm DH-BCMOA

El algoritmo que se propone a continuación es una versión híbrida y discreta del algoritmo BCMOA ideado por Guzmán et al. [16], que fue propuesto para la solución de problemas multi-objetivo en espacios continuos y basado en el comportamiento quimiotáctico de la bacteria E. Coli. En el presente trabajo se empleó la estructura del algoritmo BCMOA, la cual se adaptó con operadores evolutivos para solucionar problemas discretos. De esta hibridación se obtuvo un algoritmo que guía la búsqueda hacia soluciones que seaproximan al Frente Óptimo de Pareto. El seudocódigo del algoritmo híbrido propuesto se presenta en la figura 2.

1.2.3 Problemas de prueba de distribución de planta de celdas de manufactura - codificación y operadores

Para evaluar las aproximaciones mono-objetivo y multi-objetivo se emplearon cinco problemas de prueba cuyas matrices de secuencias, vectores de volúmenes de producción y tamaños de lotes se construyeron a partir de las matrices de incidencia que se resumen en la Tabla 1. A continuación se describe la codificación y los operadores empleados para estructurar cada problema.

Codificación de las soluciones

La codificación que se emplea para el problema de distribución de planta está basada en el grupo u orden y toma la estructura de la descripción propuesta por Gen, et al. [24]. Cada una de las soluciones se representa en un cromosoma, en el cual la primera parte corresponde a un vector que contiene la agrupación de las máquinas, a continuación la agrupación de las partes, luego la cantidad de celdas o familias de partes y, finalmente, los límites en las posiciones de las permutaciones de las máquinas y partes para conformar las celdas y familias como se muestra en las Figuras 3 y 4.

Para el ejemplo de la Figura 3, las celdas y familias de partes quedarían conformadas de la siguiente forma:

Celda 1= Máquinas 6 y 4 Familia 1= Parte 3
Celda 2= Máquinas 3, 1 y 2 Familia 2= Partes 4 y 1
Celda 3= Máquina 5 Familia 3= Parte 2

Generación de la población inicial

En este caso se generan las permutaciones para las máquinas y partes, ordenando aleatoriamente un arreglo que va desde 1 hasta el número de máquinas o partes. La cantidad de celdas se asigna con un número aleatorio entre 1 y el máximo número de celdas, el cual define la cantidad de límites en las posiciones para formar las celdas y familias asignando a éstas las máquinas o partes que quedan en los intervalos que estos definen.

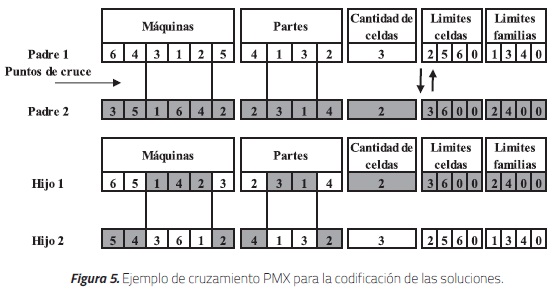
Cruzamiento

El cruzamiento se realiza recombinando las secciones del cromosoma. Las dos primeras secciones correspondientes a las permutaciones de las máquinas y las partes se cruzan empleando cruzamiento PMX (Partially Mapped Crossover). El resto del cromosoma se intercambia completamente para formar cada hijo. El proceso se ilustra en la Figura 5.

Mutación

En la mutación, las primeras secciones se del cromosoma se genera como si fuese un transforman (mutan) por inversión y el resto nuevo individuo (Figura 6).

Eliminación y dispersión

El proceso de eliminación y dispersión se realiza con aquellas bacterias que no pertenecen a la élite y obtienen una probabilidad menor a la Ped (Probabilidad de eliminación y dispersión), generando una nueva bacteria que remplaza a la original.

Quimiotaxis

La quimiotaxis implementada para el DHBFGA y el DH-BCMOA cumple la misma función exploratoria pero difiere entre sí estructuralmente. La implementada para DHBFGA se muestra en la Figura 7. Esta opera sobre las permutaciones de las máquinas y genera alternativas de solución por medio de intercambios e inserciones de las máquinas que conforman cada celda. De esta forma se generan para cada bacteria que pertenezca a la élite tantas alternativas por intercambio e inserción como celdas tenga la bacteria, con lo cual la bacteria explora entre alternativas que minimicen el costo de transporte, pero conservando el mismo agrupamiento de las máquinas en celdas. La exploración de nuevas alternativas con diferentes números de celdas y límites de éstas para formar las celdas se delega en la eliminación y dispersión.

La quimiotaxis que realiza el DH-BCMOA se describe en la Figura 8 y opera de forma jerárquica sobre todos los elementos del cromosoma. Primero, genera una alternativa por intercambio aplicando este operador a las permutaciones de las máquinas y partes. Si esta alternativa domina a la bacteria original, ésta la remplaza, de lo contario, genera otra alternativa por inserción aplicando este operador a las permutaciones de las máquinas y partes. Si esta alternativa domina a la bacteria original, ésta la remplaza, de lo contario, genera otra alternativa por inversión aplicando este operador a las permutaciones de las máquinas y partes. Si esta alternativa domina a la bacteria original, ésta la remplaza, de lo contario, genera otra alternativa asignando una nueva cantidad de celdas al cromosoma y generando nuevos límites para las celdas y familias. Si esta última alternativa domina a la bacteria original, ésta la reemplaza, de lo contrario, termina la quimiotaxis.

Reproducción por duplicación

En el BFOA la reproducción por duplicación se realizó copiando S/S_r veces las bacterias mejor adaptadas.

2. RESULTADOS Y DISCUSION

La metodología empleada para probar las propuestas presentadas consistió en, primero, evaluar el desempeño de los algoritmos propuestos con dos problemas clásicos pero genéricos, el del agente viajero TSP y el de la mochila, para luego abordar la solución de los problemas de prueba de la distribución de planta de celdas de manufactura. A continuación se describe el proceso seguido y los resultados obtenidos.

Primero se evaluó el desempeño de la propuesta mono-objetivo en la solución de cinco problemas del agente viajero que están disponibles en [25]. Los resultados se compararon con los obtenidos por versiones discretas del algoritmo genético BFOA y el algoritmo híbrido denominado Bacterial-GA foraging [14]. En la Figura 9 se puede apreciar como el algoritmo propuesto DHBFGA obtiene los mejores (más bajos) valores de fitness en 4 de los 5 problemas.

En la Figura 10 se evidencia el comportamiento de los algoritmos evaluados en el problema TSP Ch130. En ésta es claro como el algoritmo propuesto converge más rápido y obtiene para el criterio de parada (establecido en 250 000 llamados a la función fitness) el valor más bajo del fitness (mejor solución).

En las Figuras 9 y 11 se presentan los promedios de la función fitness obtenidos por los algoritmos evaluados en la solución de los problemas TSP y en los problemas de distribución de planta de celdas de manufactura. En los dos casos el algoritmo propuesto DHBFGA tiene un mejor desempeño. Se observa, que en los problemas TSP, el comportamiento de DHBFGA se aproxima más a los algoritmos basados en bacterias, mientras en los problemas de distribución de planta se asemeja más al algoritmo genético (Figuras 10 y 12). Este comportamiento evidencia el carácter híbrido del algoritmo DHBFGA propuesto.

El desempeño de la propuesta multiobjetivo se evaluó con tres variantes del problema de las mochilas [26] y cinco problemas de distribución de planta de celdas de manufactura (Tabla 1). Los resultados se compararon con los algoritmos NSGA2 [17] y SPEA2 [27]. La comparación de resultados se realizó considerando la métrica de convergencia [18] y el tiempo empleado. En la Figura 13 se aprecia que el algoritmo DH-BCMOA presenta la mejor convergencia, la cual mejora en la medida en que se incrementa la complejidad del problema y en la Figura 14 se observa como DH-BCMOA obtiene los menores tiempos en comparación con NSGA2 y SPEA2. En la Figura 15 se presenta el espacio de funciones del comportamiento de los tres algoritmos en la solución del problema multi-objetivo de las mochilas con 100 ítems. Se observa que el desempeño es similar entre los tres algoritmos para la solución de este problema.

La evaluación del desempeño de los algoritmos en la solución de los problemas multi-objetivo de las celdas de manufactura se realizó analizando el tiempo empleado por cada algoritmo para realizar 250 000 llamados a las funciones fitness. Claramente el menor tiempo en todos los problemas se obtiene con DH-BCMOA, mientras que con NSGA2 se obtienen tiempos un tanto mayores y con SPEA2 se obtienen los tiempos más altos en todos los problemas (Figura 16), lo cual se debe al uso recurrente de procesos de ordenamiento.

En cuanto a la convergencia, SPEA2 DH-BCMOA, seguido de NSGA2 (Figura 18). presenta un mejor desempeño cuando el Es decir que con el algoritmo propuesto se criterio de parada es 250 000 llamados a la obtiene una convergencia más veloz en la función fitness (Figura 17). Sin embargo, si solución de los problemas de distribución se modifica éste por un tiempo constante de de planta de celdas de manufactura y en 200 segundos, el mejor desempeño lo logra los problemas de las mochilas.

3. CONCLUSIONES

Los resultados obtenidos por los algoritmos AG, BFOA, Bacterial-GA Foraging y DHBFGA en la solución de los problemas del agente viajero y de distribución de planta de celdas de manufactura demostraron que los algoritmos basados en bacterias presentan un mejor desempeño en problemas con permutaciones, mientras que los algoritmos genéticos se comportan mejor en problemas de agrupamiento o que involucren combinaciones.

El algoritmo híbrido propuesto en este trabajo (DHBFGA) se adapta bien a los problemas TSP y de distribución de planta de celdas de manufactura logrando un desempeño del fitness y del tiempo de proceso mejores en comparación con los otros algoritmos estudiados. Este comportamiento refleja la suma de fortalezas lograda con la hibridación.

La comparación entre las soluciones al problema de las mochilas (multi-objetivo) obtenidas por los algoritmos NSGA2, SPEA2 y DH-BCMOA demuestran un buen desempeño del algoritmo híbrido propuesto en este trabajo (DH-BCMOA) en la solución de este tipo de problemas. Esto se explica por la estructura ágil que tiene BCMOA conjuntamente con la hibridación.

De igual manera que con el problema de las mochilas, en la solución multi-objetivo del problema de distribución de planta de celdas de manufactura, el algoritmo DHBCMOA demostró un mejor desempeño ya que logra mejores soluciones no dominadas en menor tiempo, para un escenario de tiempo constante. Sin embargo, el algoritmo SPEA2 para los dos tipos de problemas (mochilas y distribución de planta) presenta una buena convergencia pero en un tiempo elevado. Esto se debe a que requiere de forma recurrente procesos de ordenamiento que son costosos desde el punto de vista temporal.

AGRADECIMIENTOS

Este trabajo fue posible gracias a COLCIENCIAS quien lo financió mediante el proyecto 1101-521-28362.

REFERENCIAS

[1] Singh, N. (1996). Systems approach to computer - integrated design and manufacturing. Nueva York: John Wiley.         [ Links ]

[2] Selim, H. M., Askin, R. G. & Vakharia, A. J. (1998). Cell formation in group technology: review, evaluation and directions for future research. Computers & Industrial Engineering, 34(1), pp 3-20.         [ Links ]

[3] Papaioannou, G. & Wilson, J. M. (2010). The evolution of cell formation problem methodologies based on recent studies (1997-2008): Review and directions for future research. European Journal of Operational Research, 206(39), pp. 509-521.         [ Links ]

[4] Yin, Y. & Yasuda, K. (2006). Similarity coefficient methods applied to cell formation problem: a taxonomy and review. International Journal of Production Economics, 101(2), pp. 329-352.         [ Links ]

[5] Hamann, T., & Vernadat, F. (1992). The intra cell layout problem in automated manufacturing system. INRIA-00074957, version 1. N° Research Report -1603 (1992). Recuperado de http://hal.inria.fr/inria-00074957.         [ Links ]

[6] Elwany, M. H., Khairy, A. B. & Abou-Ali, M. G. (1997). A Combined Multicriteria Approach for Cellular Manufacturing Layout. ClRP Annals - Manufacturing Technology, 46(1), pp. 369-371.         [ Links ]

[7] Solimanpur, M., Vrat, P., & Shankar, R. (2004). Ant colony optimization algorithm to the inter-cell layout problem in cellular manufacturing. European Journal of Operational Research. 157(3), pp. 592-606.         [ Links ]

[8] Ming, L.C., & Ponnambalam S.G. (octubre, 2008). A hybrid GA/PSO for the concurrent design of cellular manufacturing system. Systems, Man and Cybernetics, 2008. SMC 2008. IEEE International Conference, pp.1855-1860.         [ Links ]

[9] Ariafar, S., Ismail, N., Tang, S.H., Ariffin, M.K.A.M. & Firoozi, Z. (septiembre, 2011). Inter-cell and intra-cell layout design in a cellular manufacturing system. Business, Engineering and Industrial Applications (ISBEIA), 2011 IEEE Symposium, pp.28-33.         [ Links ]

[10] Ho, Y. C. & Liao, T.W. (2011). A concurrent solution for intra-cell flow path layouts and I/O point locations of cells in a cellular manufacturing system. Computers & Industrial Engineering, 60(4), pp. 614-634.         [ Links ]

[11] Wu, X., Chu, C. H., Wang, Y., & Yan, W. (2007). A genetic algorithm for cellular manufacturing design and layout. European Journal of Operational Research, 181(1), pp. 156-167.         [ Links ]

[12] Solimanpur, M., Vrat, P., & Shankar, R., (2004b). A multi-objective genetic algorithm approach to the design of cellular manufacturing systems. International Journal of Production Research, 42(7), pp. 1419-1441.         [ Links ]

[13] Kumar, C.S. & Chandrasekharan, M.P. (1990). Grouping efficacy: a quantitative criterion for goodness of block diagonal forms of binary matrices in group technology. International Journal of Production Research, 28(2), pp.233-243.         [ Links ]

[14] Chen, T., Tsai, P., Chu, S., & Pan, J. (septiembre, 2007). A novel optimization approach: bacterial-GA foraging. Proceedings of the Second International Conference on Innovative Computing, Information and Control. Washington DC, EE.UU, pp.391-394.         [ Links ]

[15] Passino, K., (2002). Biomimicry of bacterial foraging for distributed optimization and control. IEEE Control Systems Magazine, 22(3), pp. 52-67.         [ Links ]

[16] Guzmán, M. A., Delgado, A. & Carvalho, J. (2010). A novel multiobjective optimization algorithm based on bacterial chemotaxis. Engineering Applications of Artificial Intelligence, 23(3), pp. 292-301.         [ Links ]

[17] Deb, K., Pratap, A., Agarwal, S. & Meyarivan, T. (2002). A fast and elitist multi objective genetic algorithm: NSGA II. IEEE Transactions on Evolutionary Computation, 6(2), pp.182-197.         [ Links ]

[18] Kumar, P., Bandyopadhyay, S., & Kumar, S. (2007). Multi-objective Particle Swarm Optimization with time variant inertia and acceleration coefficients. Information Sciences, 177(22), pp. 5033-5049.         [ Links ]

[19] Vitanov, V., Tjahjono, B. & Marghalany, I. (2008). Heuristic rules-based logic cell formation algorithm. International Journal of Production Research, 46(2), pp. 321-344.         [ Links ]

[20] Seifoddini, H. & Djassemi, M. (1996). A New Grouping Measure for Evaluation of Machine-Component Matrices. International Journal of Production Research, 34(5), pp. 1179-1193.         [ Links ]

[21] King, J.R. (1980). Machine-component group formation in group technology. Omega, 8(2), pp. 193-199.         [ Links ]

[22] Burbidge, J. L. (1969). An Introduction of Group Technology. Proceedings of Seminar on Group Technology. Turín, Italia: Birniehill Institute.         [ Links ]

[23] Chandrasekharan, K. P. & Rajagopolan, R. (1989). Groupability: an analysis of the properties of binary data for group technology. International Journal of Production Research, 27(6), pp. 1035-1052.         [ Links ]

[24] Gen, M., Lin, L. & Zhang, H. (2009). Evolutionary techniques for optimization problems in integrated manufacturing system: State of art survey. Computers & industrial engineering, 56(3), pp. 779-808.         [ Links ]

[25] The TSPLIB Symmetric Traveling Salesman Problem. (s.f.). Recuperado el 15 de junio de 2012, de http://elib.zib.de/pub/mp-testdata/tsp/tsplib/tsp/index.html.         [ Links ]

[26] Zitzler, E. & Laumanns, M. (s.f). Test problems and test data for multiobjective optimizers. Recuperado el 21 de junio de 2012, de http://www.tik.ee.ethz.ch/sop/download/supplementary/testProblemSuite/.         [ Links ]

[27] Zitzler, E., Laumanns, M., & Thiele, L. (mayo, 2001). SPEA2: Improving the strength pareto evolutionary algorithm for multiobjective optimization. Technical report TIK-103, Computer Engineering and Network Laboratory (TIK). Zurich, Suiza.         [ Links ]

[28] Deb, K. & Jain, S. (2002). Running performance metrics for evolutionary multi-objective optimization. KanGal Report No. 2002004, Kanpur Genetic Algorithms Laboratory, Indian Institute of Technology. Kanpur, India.         [ Links ]