Introducción

Los problemas de propagación del sonido pueden ser encontrados en diversas situaciones, por ejemplo, en el diseño y mejoramiento de instrumentos musicales, en la construcción de recintos y cavidades sonoras, y en el control de ruido. Es de interés, entre otros, el estudio de fenómenos de reflexión y transmisión de ondas acústicas en paredes o fronteras, el análisis modal de ondas sonoras, el aislamiento acústico y la pérdida de transmisión. Sin embargo, solo un limitado tipo de problemas en este rango tiene solución analítica, en particular aquellos donde las condiciones de frontera no sean muy complicadas y los fenómenos de disipación y transmisión puedan simplificarse de manera suficiente. Por ello, es necesaria e importante la implementación de métodos numéricos que puedan ofrecer soluciones válidas ante los procesos de generación, transmisión y recepción de sonido.

Este trabajo se enfoca específicamente en la modelación y simulación de la propagación de ondas sonoras en el interior de un tubo acústico de longitud finita. Las ecuaciones acústicas que modelan el problema conforman un sistema hiperbólico acoplado de primer orden. Este sistema tiene la ventaja sobre el modelo habitual—la ecuación de Helmholtz— de examinar situaciones más generales que el hecho de considerar la propagación y dispersión de ondas sonoras armónicas [¹]-[⁵]; además, permite estudiar nuevos sonidos complejos de gran interés en la música electroacústica y computacional [⁶] y [⁷].

Desde el punto de vista numérico, empleamos un esquema de diferencias finitas escalonado que ha mostrado su fortaleza en otros contextos donde el dominio espacial no es acotado [⁸]-[¹²]. En contraste con estos trabajos, aquí consideramos un dominio acotado en el cual se debe realizar un tratamiento de discretización cuidadoso de las condiciones de frontera (ver en la sección “Valores de la frontera para las ecuaciones discretas”). Una vez que validamos el método contrastando los resultados obtenidos con los esperados teóricamente, estudiamos el comportamiento de la presión y la velocidad en el interior del tubo cuando se varía de manera aleatoria la velocidad del pistón, lo que genera un patrón de ondas acústicas. Además, presentamos un análisis modal vía transformada rápida de Fourier FFT para analizar las señales aleatorias de salida del sistema.

Este artículo está organizado así: en la sección “Modelo matemático” se presentan las ecuaciones que describen la dinámica de las ondas sonoras en el interior del tubo, así como las condiciones de frontera. El esquema de discretización escalonado y tratamiento numérico de las condiciones de frontera se describe en la sección “Diferencias finitas escalonadas”. En el apartado “Resultados numéricos” se presenta el estudio de las ondas de presión en una de las paredes del tubo vía simulación numérica, y también el análisis modal del tubo. Por último, se exponen algunas conclusiones.

Modelo matemático

Consideremos un tubo largo y delgado, de longitud L y en su extremo izquierdo (x=0) se encuentra un pistón que funciona como fuente sonora, es decir, es una fuente de velocidad v_p(t) de las partículas de aire confinadas en el interior del tubo. En x=L está la pared derecha del tubo, que consiste en una superficie semirrígida de impedancia Z(ver Figura 1).

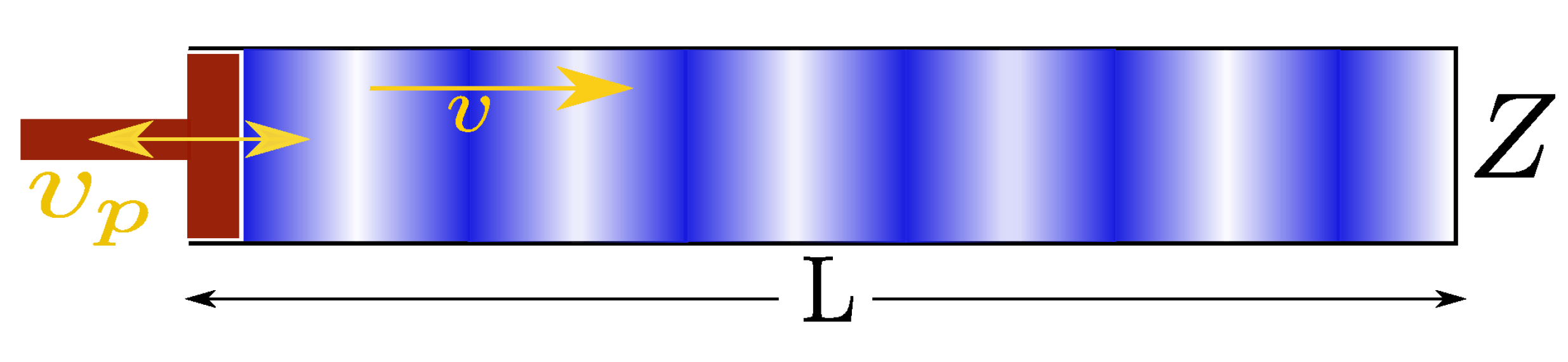
Fig. 1. Tubo delgado con pistón móvil en x =0 y cerrado en x=L por una pared semirrígida con impedancia Z. Fuente: elaboración propia 

La perturbación producida por el movimiento del pistón da origen a una onda sonora, lo que modifica el estado de movimiento del aire a través del tubo e induce cambios de presión y densidad de partículas en el aire. Estos cambios ocurren rápidamente, de manera que no hay tiempo suficiente para el intercambio de calor. Considerando que la presión P, la velocidad v, las fluctuaciones de densidad p, junto con las derivadas de estas cantidades son pequeñas y empleando las leyes de conservación de masa y momento, tenemos que las ecuaciones que describen la dinámica del aire en el interior del tubo son [¹³]:

En cuanto a los extremos del tubo, observamos que:

En x=0 se encuentra un pistón, que al ponerse en movimiento, las partículas de aire que están en contacto con él se mueven con la misma velocidad, por lo cual:

En la pared situada en x=L se observa que cuando la onda de presión (partículas en movimiento) choca con la pared ocurre una atenuación de la onda sonora, es decir, un porcentaje de la energía acústica se pierde en la deformación microscópica de la pared. Este fenómeno se describe por:

Donde Z es una constante positiva llamada impedancia acústica y da cuenta de la capacidad del material de impedir la transmisión de ondas sonoras incidentes en él.

Como condiciones iniciales del modelo consideramos que en el instante t=0 el aire al interior del tubo está en reposo y la presión es la atmosférica, es decir:

v(x,0) = 0 p(x,0) = 0.

Nota 1. El sistema de ecuaciones (1) y (2) puede reducirse a la ecuación de onda de segundo orden; sin embargo, observamos que la condición de frontera sobre la pared derecha del tubo aparece tanto en el término de velocidad v(L,t) como en el de presión p(L,t) relacionadas por el factor Z, lo cual motiva fuertemente la posibilidad de trabajar directo sobre el sistema de ecuaciones acoplado de primer orden.

Para calcular una aproximación numérica de la solución del sistema de ecuaciones diferenciales (1) y (2) con condiciones de frontera (3) y (4), construimos la siguiente discretización del dominio espacio tiempo. La malla consta de los puntos:

Donde Δx y Δt son los tamaños de paso de discretización en espacio y tiempo, respectivamente (ver Figura 2).

Fig. 2. Esquema de malla escalonada. 

Sobre esta malla calculamos los valores de presión en los puntos (x_i, t_n) y los valores de la velocidad en puntos (x_i + Δx / 2,t_n + Δt / 2). Como resultado, los valores discretos de la presión P y la velocidad v se localizan en dos mallas separadas. Así, denotamos con

Con i = 0,1,...,M y n = 0,1,... .

De esta forma, empleando diferencias centrales para aproximar las derivadas en tiempo y en espacio tenemos:

Reemplazando estas discretizaciones en el sistema (1) - (2), obtenemos las ecuaciones acústicas en el dominio discreto espacio-temporal:

Los términos del sistema discreto (8) - (9) están organizados de tal forma que conseguimos un método explicito, en el cual los valores de la velocidad en el instante t_n+1/2 pueden calcularse directamente de los valores de la velocidad y la presión en los instantes anteriores t_n-1/2 y tn, respectivamente, y la presión en el instante t_n+1 se calcula a partir de la presión y la velocidad en los instantes t_n-1 y t_n+1/2.

Valores de la frontera para las ecuaciones discretas

Dada la construcción del esquema de diferencias finitas propuesto, las condiciones de frontera (3) y (4) requieren atención especial en la implementación numérica de nuestro problema.

En la Figura 3 observemos que los valores de la velocidad solo se calculan en los nodos x_i+1/2, i=1,...M -1, por lo cual ubicamos el pistón en el punto x_1/2=0 dentro de la malla, de forma que el nodo x₀ queda por fuera del sistema. Entonces, la discretización de la condición de frontera (3) es:

Fig. 3. Red escalonada para la solución numérica de las ecuaciones (1) y (2) 

En cuanto a la condición de frontera (4), requerimos los valores de la velocidad y la presión en la pared. Para ello definimos la posición de la pared derecha dentro de la malla espacial en el punto x_M-1/2 = L, como se ilustra en la Figura 3. Nótese entonces que Δx = L / (M - 1).

Empleando la fórmula (8), la velocidad en el punto x_M-1/2 está dada por:

Pero esta expresión involucra el valor de la presión en x_M, punto que está fuera del sistema. Para superar este inconveniente, aproximamos el valor de la derivada espacial de la presión en x_M por una diferencia finita regresiva. Luego, la velocidad en la pared derecha del tubo es:

La fórmula (12) exige el cálculo de la presión en el punto x_M-1/2, donde la presión no está definida. Empleando la condición de frontera (4):

Se obtiene que la presión en el punto (x_M-1/2,t_n) está definida en términos de la velocidad en el mismo punto. Así, el problema de calcular la presión en el punto x_M-1/2 del eje espacial se traslada al cálculo de la velocidad en el instante t=t_n, donde no está definida. Sin embargo, interpolando linealmente en la coordenada temporal entre los valores (ver Figura 2) se tiene que:

Al sustituir (14) en (13), esta se convierte en:

Ahora, volviendo a la expresión (12), sustituimos el valor para la presión . Al agrupar y organizar términos se obtiene que:

Nota 2. Uno de los objetivos de construir la malla escalonada es tener una aproximación de orden:

de las derivadas espaciales y temporales de la presión y la velocidad, como lo podemos ver en (7). No obstante, al emplear las diferencias regresivas (12) y la interpolación lineal (14) en la discretización de la condición de frontera en la pared derecha (4), el error de aproximación de la solución decae a orden:

Resultados numéricos

En esta sección estudiamos, mediante experimentación numérica, fenómenos acústicos como el efecto producido por el tipo de material de la pared y el factor de calidad del tubo; asimismo, realizamos un análisis modal del tubo cuando el movimiento del pistón es armónico y aleatorio. En todos los cálculos se considera que L = 1.0m, c-330m/s, p=1.3Kg/m³, Z = 6000 Pas/m y un comportamiento oscilatorio del pistón dado por vp =v₀sin(2π ft) con v₀=1_m/s y f=170 Hz (Figura 4, izquierda). Para garantizar la estabilidad y convergencia del método, los tamaños de paso de discretización en espacio y tiempo se escogen de tal manera que la condición CFL, cΔt / Δx <1 (Ver [¹⁴]) se satisface; estos son Δx=0.01m y Δt=3.03x10^-5 s.

A continuación, analizamos el efecto de la condición de frontera en la pared derecha del tubo.

Influencia del material de la pared

En la Figura 4 (a la derecha) se presenta el comportamiento de la presión acústica en x=L respecto al tiempo. Se observa un primer momento cuando la energía suministrada por el pistón empieza a manifestarse sobre la pared derecha del tubo, con un comportamiento creciente de la amplitud de la onda de presión.

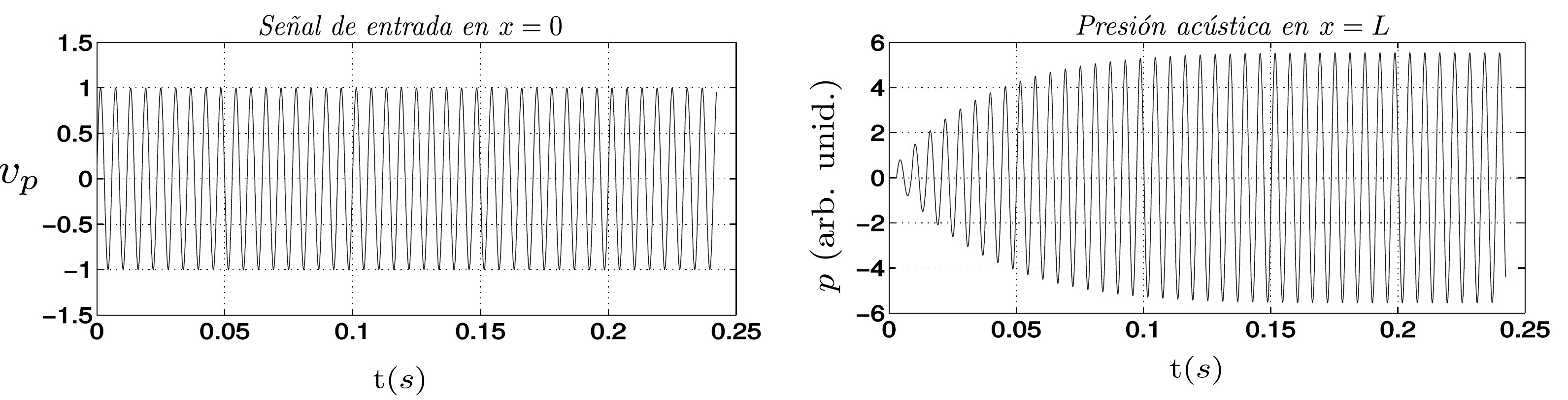
Fig. 4. Señal armónica de entrada en el pistón y respuesta en la pared del tubo como función del tiempo. 

Si este proceso continúa con estas condiciones, el aumento tiene lugar de forma indefinida; sin embargo, una vez llega el pulso a la frontera, un fenómeno de disipación debido a la pared semirrígida hace que este aumento se detenga. Esta etapa corresponde al estado estacionario del sistema que se observa en el comportamiento sinusoidal de amplitud constante de la gráfica.

Si no ocurre una pérdida de energía, el fenómeno de presión creciente permanece de manera indefinida. Podemos modelar esta situación tomando Z→∞ (ver Figura 5). Por lo tanto, el tiempo que tarda el sistema en alcanzar el estado estacionario está directamente relacionado con la impedancia en la frontera, esto es, con las características intrínsecas del material. Este montaje tipo pistón-tubo acústico se usa en la medición de la impedancia acústica de distintos materiales. Por este motivo, se conoce también como tubo de impedancias.

Fig. 5. Aumento indefinido de la presión acústica con Z→∞ 

Suspensión repentina de la señal

Ahora estudiamos el fenómeno meramente disipativo que ocurre en la pared del tubo. Para ello, comenzamos con una señal armónica en el pistón, como en el caso anterior, y dado un tiempo suficiente para que se alcance el estado estacionario detenemos de manera súbita el movimiento en el pistón. El resultado de la presión en la pared del tubo se observa a la derecha en la Figura 6.

Al detener el pistón, la ganancia de energía del sistema se anula y da lugar solo a las pérdidas generadas por el choque de las partículas con la pared derecha. Esto sugiere, además, que el proceso de pérdida de energía está relacionado con la impedancia Z del material en la pared. La Figura 6 muestra un decaimiento de presión aparentemente exponencial; esto lo verificamos capturando los puntos sobre la envolvente del decaimiento y analizamos su gráfica aislada con escala logarítmica. El resultado se ilustra en la Figura 7. El comportamiento lineal prueba que en efecto la amplitud está gobernada por una función decreciente del tipo e^-yt.

Fig. 6. Suspensión súbita de la señal de entrada armónica. 

Fig. 7. Decaimiento exponencial de la amplitud en presión luego de suspender la señal del pistón 

Factor de calidad e impedancia acústica

La relación entre el decaimiento exponencial que acabamos de observar y la impedancia Z tiene un significado mucho más profundo a la luz de la teoría de osciladores armónicos. Para un valor fijo de x=L en nuestras ecuaciones acústicas, la presión p(L,t) puede ser vista como un problema de oscilador forzado-amortiguado. El forzamiento proviene de la acción armónica del pistón en x=0, que se propaga en el interior del tubo hasta llegar a la pared opuesta.

Por otro lado, el factor de amortiguamiento se relaciona con la impedancia acústica Z. Para respaldar este análisis recurrimos al concepto de factor de calidad ^Q . Esta variable adimensional se define como la razón entre la frecuencia natural del sistema y un factor de amortiguamiento. En otros términos, podemos decir que en un proceso de decaimiento, como se observa cuando se suspende el movimiento del pistón, la amplitud de la presión acústica se comporta según la fórmula:

Esto significa que la amplitud de oscilación disminuye en un factor de 1/e al cabo de Q / p ciclos de oscilación.

A su vez, la impedancia acústica Z determina la rapidez con que se disipa la energía en la pared derecha; por tanto, resulta natural preguntarse la relación entre estas dos magnitudes. Al analizar el proceso de decaimiento para distintos valores de la impedancia Z del sistema y determinar para cada uno de ellos el factor de calidad usando la expresión (16), encontramos la relación de la Figura 8. La dependencia lineal es evidente, y el factor de proporcionalidad se calcula mediante regresión lineal.

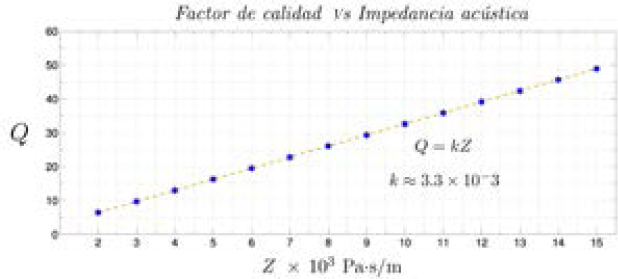
Fig. 8. Dependencia lineal entre el factor de calidad Q y la impedancia Z para oscilaciones de la presión acústica en x=L 

Por último, constatamos la validez teórica de todo el tratamiento numérico detrás de este análisis: una mayor impedancia Z, implica menor pérdida de energía; a su vez, un mayor factor de calidad significa mayores ciclos de oscilación antes del decaimiento total de la amplitud de la onda de presión. Vale decir que este tipo de decaimiento en sistemas de oscilación libre mostrará también una respuesta selectiva en frecuencias de resonancia ante una señal impulsora, como veremos en la siguiente sección.

Análisis modal

En esta sección se estudia la dependencia de la intensidad del sonido con la frecuencia de vibración impartida por el pistón para dos casos: cuando el pistón tiene un movimiento oscilatorio armónico y cuando este se mueve aleatoriamente.

Movimiento armónico del pistón

Para examinar este comportamiento sobre el esquema computacional, hacemos un barrido de frecuencias en el intervalo [0Hz-1000Hz] sobre el montaje anterior. Una vez que se alcanza el estado estacionario, determinamos la intensidad sonora en cada caso, a partir del cálculo de la velocidad media cuadrática del aire 〈v²〉 sobre todo el sistema. La medida de 〈v²〉 esta relacionada directamente con la presión sonora, la cual da idea de la intensidad acústica. En la Figura 9 se presenta el resultado de este análisis y se observa un comportamiento selectivo con forma de picos de alta intensidad para un conjunto de frecuencias específicas. Estas últimas son precisamente las frecuencias de resonancia del sistema.

Fig. 9. Análisis mediante el cálculo de 〈v²〉 

Es conocido que las frecuencias de resonancia de un tubo con paredes abiertas están dadas por [¹¹]. Al comparar estás frecuencias con los resultados obtenidos (Tabla 1), observamos que los valores de las frecuencias en los picos conseguidos se aproximan a las frecuencias de resonancia del tubo con paredes abiertas. Esta analogía establece una relación entre un tubo acústico de una determinada impedancia perturbado por un pistón en su extremo opuesto y un tubo de condición de frontera abierta con las mismas condiciones.

Tabla 1. Frecuencias de resonancia para un tubo acústico con impedancia Z = 6000 Pa ×s / m/ (f_num frecuencia numerica) 

n	1	2	3	4	5
fnum (Hz)	170	335	506	670	840
f(L=1m (Hz)	165	330	495	660	825

Movimiento aleatorio del pistón (ruido blanco)

Otro caso de gran interés es el de dotar al pistón de un movimiento aleatorio. Como consecuencia, el tubo estará sometido a una señal de ruido, conocida como ruido blanco, una señal de tipo estocástico que contiene todas las frecuencias con amplitudes distribuidas de manera aleatoria.

Implementamos esta señal computacionalmente generando números aleatorios uniformemente distribuidos en el intervalo (-v₀,v₀). En la Figura 10, parte izquierda, se observa el comportamiento aleatorio de la señal de entrada. En la parte derecha se muestra la señal de presión alcanzada en la pared del tubo, que a primera vista parece ser también totalmente aleatoria; no obstante, esta señal presenta una característica muy particular.

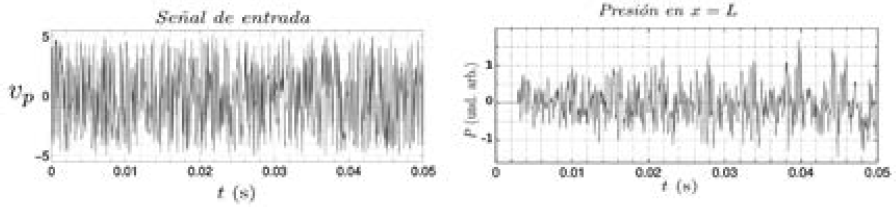
Fig. 10. Señal de ruido blanco en el pistón y su correspondiente respuesta de presión acústica en x=L 

Para develar con mayor precisión el comportamiento de este tipo de señales, conviene hacer uso del análisis de Fourier; es decir, un análisis de las frecuencias características que las componen y de sus correspondientes amplitudes.

Aplicando la transformada rápida de Fourier (FFT) [¹⁴] y [¹⁵], tanto a la señal de entrada como a la respuesta en presión en un intervalo de (0-1000) Hz, se obtienen los espectros de frecuencia de cada señal (ver Figura 11). Es evidente que el espectro de la señal de entrada corresponde al conjunto de todas las frecuencias con amplitudes aleatorias, una característica típica de la señal de ruido; por otro lado, el resultado obtenido para el espectro de presión resulta más interesante. No todas las frecuencias están presentes con la misma intensidad, incluso solo para un conjunto muy específico de ellas existen picos de alta intensidad. Las frecuencias de máxima intensidad se muestran en la Tabla 1.

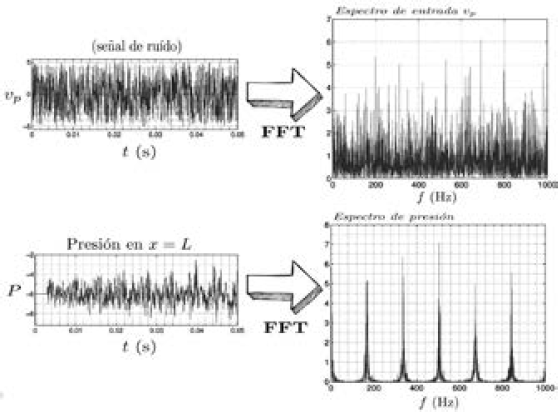
Fig. 11. Espectros de frecuencia para la señal de entrada (ruido blanco) y para la presión de salida utilizando FFT 

Tabla 2. Frecuencias de resonancia obtenidas a partir del espectro de presión 

n	1	2	3	4	5
fnum (Hz)	170	335	504	672	841

Se observa que los valores de las frecuencias de resonancia obtenidas a partir de una señal de ruido aleatoria coinciden con los valores calculados para una señal armónica; por lo tanto, el tubo se comporta como un filtro que permite el paso de un conjunto específico de frecuencias. Además, por ser este el conjunto de frecuencias de resonancia del tubo, todas son múltiplos enteros de una frecuencia fundamental. La señal de ruido en la entrada del pistón se transforma así en una señal en la que predomina un tono puro (la primera frecuencia), acompañado de sus armónicos correspondientes, semejantes al sonido de una flauta. Por otra parte, las frecuencias denominadas frecuencias de antirresonancia son anuladas en el interior del tubo, y no contribuyen a la frontera de manera considerable.

Un comportamiento de este tipo es propio de un filtro acústico, un dispositivo capaz de seleccionar de manera conveniente un conjunto de frecuencias, lo que permite el paso de unas e impide el paso de otras. En general, el fenómeno fundamental detrás de los filtros acústicos es la resonancia. Su estudio es muy importante, tanto en el mejoramiento de potencia y calidad para algunos instrumentos musicales (por ejemplo, la caja acústica de una guitarra o violín), como en la construcción de silenciadores aplicables a ambientes ruidosos de alto riesgo para la salud.

Conviene anotar que el espectro que se determina en este esquema está relacionado directamente con los valores propios del operador que surge en el tratamiento analítico. Su solución, por esta vía y por la vía numérica, permite encontrar las frecuencias de resonancia del sistema; sin embargo, resolver analíticamente el problema de una señal de entrada v_p(t), del tipo ruido blanco, representa una dificultad que motiva muy poco esta búsqueda. Los métodos numéricos, como el que hemos utilizado, presentan una alternativa práctica y eficiente en este sentido.

Conclusiones

Los métodos de análisis numérico de tipo malla escalonada, aplicados a las ecuaciones que modelan fenómenos acústicos en el interior de un tubo sonoro (régimen lineal), permiten simular la propagación de ondas en dicho sistema, así como fenómenos de resonancia, reflexión, transmisión y decaimiento.

El análisis de frecuencias usando el algoritmo de FFT comprueba el comportamiento acústico resonante de un tubo sonoro, aun cuando la perturbación al nivel del pistón sea una señal de ruido aleatoria; esto permite destacar las propiedades selectivas del tubo semejantes a un filtro acústico de ruido.

Por último, el método numérico utilizado permite analizar y predecir el comportamiento de condiciones de frontera propias del fenómenoacústico real, teniendo en cuenta el factor de impedancia acústica.