Introducción
Colombia ha sufrido grandes consecuencias socioeconómicas en las últimas décadas debido a la ocurrencia de eventos naturales peligrosos. Estos han sido determinantes para retardar el crecimiento económico de corto y largo plazo del país, pues han ocasionado destrucción de la infraestructura física, de los recursos naturales y del capital humano nacional [1], [2].
Para dimensionar la magnitud del problema, se estima que no adaptarse al cambio climático le puede generar pérdidas del 0.5 % del PIB, que corresponden a cerca de 3,8 billones anualmente [3]. La vulnerabilidad del país ante eventos climáticos es tal, que sucesos importantes como el fenómeno de La Niña le generaron pérdidas al Estado por 11,2 billones de pesos entre 2010 y 2011, mientras que El Niño 2015-2016 mermó la producción nacional en 3,1 billones [4].
De acuerdo con la Unidad Nacional para la Gestión del Riesgo de Desastres, el 88 % de los desastres naturales ocurridos en Colombia es de origen hidrometeorológico, distribuidos así: un 37 % debido a sequías e incendios, un 35 % a inundaciones, un 15 % a movimientos en masa y un 1 % a flujos torrenciales [2], [3].
Aunque no predominan en cantidad, los movimientos en masa o deslizamientos son el tipo de desastre natural que ha generado más pérdidas humanas en los últimos años, porque abarca el 66 % del total de muertes relacionadas con fenómenos hidrometeorológicos [2]. El censo del Departamento Administrativo Nacional de Estadística del 2018 soporta esta estimación, hallando que más del 82 % de la población en Colombia se encontraba expuesta a amenaza alta por movimientos en masa [5].
Paralelamente, la inadecuada gestión territorial en Colombia intensifica el potencial destructivo de los desastres naturales y, por consiguiente, la vulnerabilidad de las comunidades. Este es el caso de la avenida torrencial que afectó a Mocoa en 2017, que dejó más de trescientas personas muertas, cuyos efectos se clasifican como técnicamente previsibles y, por tanto, evitables [6], [7].
A pesar del riesgo natural latente, en el país existe poca alineación entre la inversión y el riesgo económico que suponen los desastres naturales. El indicador de inversiones en función del riesgo departamental demuestra que el 87.5 % de los departamentos presenta una inadecuada alineación de la inversión pública en adaptación para responder a sus niveles de riesgo [4], mientras que el Departamento Nacional de Planeación indica que Colombia debe aumentar la inversión en 2,3 billones de pesos anuales para cumplir con los objetivos de mitigación de desastres naturales [8].
Debido a la necesidad de reducir la vulnerabilidad de las comunidades, en este artículo se insiste en el uso de sistemas de monitoreo durante las etapas de planeación, construcción y mantenimiento de infraestructuras civiles, como herramientas de apoyo en los procesos de prevención y mitigación del riesgo, para disminuir los efectos de los desastres naturales.
Algunos sistemas emplean técnicas tradicionales de instrumentación y monitoreo de deslizamientos, como el control topográfico, GPS diferencial, extensómetros e inclinómetros, con los que se busca medir los desplazamientos de terrenos en puntos específicos dentro de masas inestables [9] - [11]. A día de hoy existen también otras técnicas para monitorear movimientos de tierra como el procesamiento de imágenes satelitales [12], [13] o las redes de sensores inalámbricos aprovechando la red de telefonía celular [14]. Sin embargo, actualmente los sensores de fibra óptica han ganado una amplia popularidad, debido a su facilidad de implementación y a su gran sensibilidad [15], [16].
Algunas de las técnicas de sensado fotónico usan la misma fibra óptica como sensor, como en el caso de la reflectometría óptica, en donde se envía un pulso a través de la fibra, el cual se refleja en el sitio donde ocurre una perturbación. Esta técnica puede ser en el dominio del tiempo (Optical Time Domain Reflectometry [OTDR]) [17] o en el dominio de la frecuencia (Optical Frecuency Domain Reflectometry [OFDR]) [18]. Otra técnica de sensado fotónico se basa en la dispersión estimulada de Brillouin conocida como método Brillouin Optical Time Domain Analysis [BOTDA] [19].
Mediante este método se convierte la fibra óptica en un sensor que aprovecha el efecto no lineal de Brillouin [20], [21].
Una técnica final que ha emergido recientemente como alternativa para el monitoreo estructural en muchas aplicaciones es el uso de rejillas de Bragg en fibra óptica (Fiber Bragg Gratting [FBG]), gracias a su bajo costo, facilidad de uso y alta sensibilidad [22], [23], las que fueron escogidas en este trabajo para la implementación del prototipo de monitoreo de movimientos de tierra. Por este motivo, se dedican los siguientes subtítulos a explicar las ventajas y el principio de funcionamiento de esta tecnología.
A partir de lo anterior, en este trabajo se propone y se presenta la implementación de un prototipo de sistema de monitoreo de movimientos de tierra en masa empleando sensores de fibra óptica FBG. El sistema consta de una maqueta para emular un terreno que se desea monitorear, más los elementos de sensado denominados inclinómetros fotónicos, que consisten en pequeñas barras de fibra de vidrio instrumentadas con dos sensores FBG, el sistema de interrogación y un algoritmo analítico basado en la teoría de mecánica de materiales, que tiene como propósito generar un vector con la dirección del movimiento de tierra en masa, a partir de la medida de deformación entregada por las FBG.
El documento está organizado de la siguiente manera: más adelante en este título se describen algunos conceptos teóricos sobre el comportamiento de los movimientos de tierra en masa, así como del principio de funcionamiento de los sensores FBG y la teoría de mecánica de materiales en la que se basa el algoritmo analítico de procesamiento. En la sección de materiales y métodos se describe la implementación o configuración realizada en cada una de las partes que conforman el sistema de monitoreo. Luego se presentan los resultados experimentales y, finalmente, las conclusiones del proyecto.
A continuación, se describen los conceptos y tecnologías que se deben tener claros para la comprensión del prototipo implementado para el monitoreo de movimientos de tierra en masa. Se parte de un análisis de los principales tipos de movimientos de tierra en masa y de algunas de las técnicas actuales para el monitoreo de estos fenómenos; posteriormente se describe el principio de funcionamiento de los sensores fotónicos haciendo énfasis en las FBG. Finalmente se incluyen las ecuaciones de la mecánica de materiales utilizadas para el diseño de vigas, ya que estas fueron la base para la implementación de los inclinómetros fotónicos y del algoritmo analítico para la identificación de los movimientos.
Movimientos en masa
Para definir un movimiento de tierra en masa, se debe empezar por comprender el concepto de ladera o talud, es decir, una masa de tierra que posee pendiente o cambios de altura significativos. Técnicamente, se define como ladera cuando la conformación tuvo como origen un proceso natural y talud cuando se formó artificialmente [1]. Partiendo de la definición de ladera, el término movimiento en masa se define como aquellos movimientos ladera abajo de una masa de roca, de detritos o de tierras por efectos de la gravedad, entendiéndose por detritos el material suelto de las rocas [24], [25].
Existen varios sistemas para clasificar los movimientos de tierra en masa; sin embargo, el más utilizado es el sistema propuesto por Varnes en 1978, que emplea como criterios de clasificación el tipo de movimiento y el tipo de material. Según el primero, se dividen en cinco tipos: caídas, vuelcos, deslizamientos, propagaciones y flujos. Los materiales se dividen en rocas y suelos y, a la vez, los suelos se subdividen en detritos y tierra [24], [26], [27].
El principal interés de este trabajo consiste en lograr el monitoreo de movimientos de tierra que abarquen amplias extensiones de tierra como los deslizamientos, las propagaciones laterales y los flujos, ya que estos ocurren de forma lenta principalmente por efecto de acumulación de aguas lluvia en los poros del suelo [28]; sin embargo, estos eventos también se pueden presentar debido a cambios topográficos, sismicidad, flujos de agua subterránea, cambios en la resistencia del suelo, meteorización o factores de tipo antrópico o natural que modifiquen su estado natural de estabilidad [29], [30].
Los movimientos en masa -conocidos como deslizamientos- consisten en movimientos de ladera debajo de una masa de roca o suelo y un desplazamiento que ocurre a lo largo de una o varias superficies, que se pueden detectar dentro de una zona relativamente delgada. Es un movimiento progresivo, que no se inicia al mismo tiempo en lo que sería la superficie de falla, por lo que puede comprender varias masas semiindependientes [1], [29]. En la figura 1 se presenta gráficamente un deslizamiento.
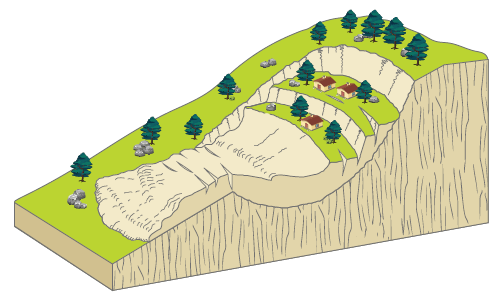
Fuente: elaboración propia con aportes de [31], [32].
Figura 1 Movimiento de tierra tipo deslizamiento
Los deslizamientos se clasifican en dos subtipos: 1) rotacionales, un movimiento en el cual la masa se mueve a lo largo de una superficie de falla curva o cóncava y 2) traslacionales, la masa se mueve a lo largo de una superficie de falla plana u ondulada [32].
A su vez, la propagación lateral es un tipo de movimiento en masa en el que el desplazamiento ocurre en gran parte por la deformación interna del material [32]. Las propagaciones laterales se pueden considerar como la fase final de una serie de movimientos en los que predomina la deformación interna, causando fragmentación del terreno en bloques grandes, como se muestra en la figura 2.
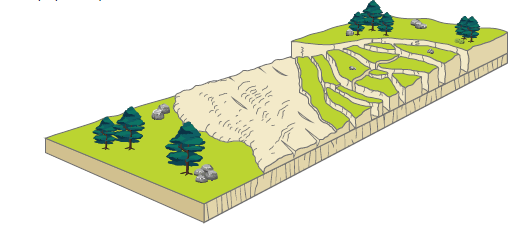
Fuente: elaboración propia con aportes de [33].
Figura 2 Movimiento de tierra tipo propagación lateral
Finalmente, los movimientos en masa tipo flujo son aquellos que durante su desplazamiento exhiben un comportamiento semejante al de un fluido, que puede ser rápido o lento, saturado o seco y, en muchos casos, se originan a partir de otro tipo de movimiento, por ejemplo, un deslizamiento [32].
Sensores fotónicos
En general, los sensores fotónicos modifican una característica de la luz guiada, en respuesta a una variable externa física, química o biológica [34]. Por ejemplo, si un componente fotónico como la fibra óptica es deformado, ocurren cambios en la atenuación, fase y polarización de la señal óptica, que pueden detectarse con los componentes adecuados.
Las ventajas que ofrecen los sensores fotónicos con respecto a los sensores mecánicos y eléctricos son: inmunidad a la interferencia electromagnética (las señales eléctricas afectan la medida de los sensores eléctricos), seguridad al no generar chispa (muy útil en ambientes como minas o en ambientes de desastre), alta confiabilidad y estabilidad (los sensores eléctricos y mecánicos requieren de calibración periódica y presentan histéresis), registran bajo consumo de potencia y no requieren alimentación eléctrica en el punto de sensado, haciéndolos aptos para el monitoreo remoto en tiempo real [34], [35].
Estas ventajas han permitido que se extienda el uso del sensado fotónico al monitoreo de la salud estructural en aeronaves y que sea comúnmente aplicado en las industrias médica, biomédica, petrolera, industrial, agropecuaria, en aplicaciones ambientales, de producción de energía eléctrica, así como en el sector militar y en la detección de sustancias químicas o biológicas [35].
Rejillas de Bragg en fibra óptica
Los sensores ópticos basados en rejillas de Bragg son probablemente los más utilizados por su bajo costo y facilidad de uso [22].
Una FBG consiste en una perturbación periódica del índice de refracción del núcleo de una fibra inducida por un láser acorde con el principio de fotosensibilidad [36], [37]. En la figura 3 se presenta un esquema del principio de funcionamiento de una FBG.
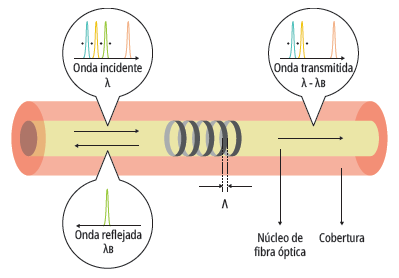
Fuente: elaboración propia con aportes de [39]-[41].
Figura 3 Principio de funcionamiento de una FBG
Cuando se introduce una fuente de luz de espectro ancho dentro de la fibra óptica que contiene la FBG, se refleja la parte del espectro de la fuente que corresponde a la longitud de onda de Bragg (λB = 2nΛ), condición de resonancia de la red, donde n es el índice de refracción efectivo y A el periodo de la modulación) y, por otra parte, el resto del espectro se transmite normalmente [38].
La longitud de onda reflejada también depende de perturbaciones externas de temperatura y tensión en la fibra óptica. De modo que la longitud de onda reflejada por la FBG cambia en una magnitud ΛλB con respecto a la deformación y la temperatura. Teniendo en cuenta esto, las FBG son a la vez sensores de deformación y temperatura. Los valores típicos de respuesta de una FBG ante ambas variables son 1.2 pm/fte y 10 pm/°C, respectivamente [38].
Dada la practicidad de los sensores FBG, estos se utilizaron para instrumentar vigas cilíndricas de fibra de vidrio, de tal modo que se pueda medir el desplazamiento del suelo en un punto determinado, a partir de la medida de deformación que realizan las FBG sobre las vigas cuando estas se deflectan. Para comprender esto mejor, en la siguiente sección se describen detalladamente los criterios mecánicos utilizados para el desarrollo de este trabajo [36].
Mecánica de materiales para el diseño de los inclinómetros fotónicos
El principio de funcionamiento de los inclinó-metros fotónicos implementados en este trabajo se basa en el análisis de la deflexión de una viga empotrada en uno de sus extremos, como la que se presenta en la figura 4.
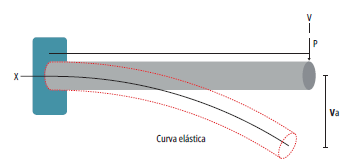
Fuente: elaboración propia con aportes de [42].
Figura 4 Deflexión de una viga empotrada en un extremo
En la figura 4 también se advierte la representación gráfica de la deflexión que, de acuerdo con el análisis de estructuras, hace referencia a la deformación que se presenta en un elemento estructural (en este caso una viga de longitud L desde el empotramiento) cuando se le aplica una fuerza P. La representación gráfica de la deflexión en el eje longitudinal, que pasa por el centroide de cada área transversal de la viga, se llama curva elástica. El desplazamiento v A que se presenta cuando la viga se deflecta se puede calcular mediante la ecuación (1):
Donde P es la fuerza aplicada, E es el módulo de elasticidad del material e I es el momento de inercia del área transversal de la viga respecto al eje neutro. Dado que el área transversal es circular, el momento de inercia está dado por I = (π/)r 4, donde r es el radio del área transversal de la viga.
De la ecuación (1), el único parámetro desconocido es la fuerza P. No obstante, esta se puede deducir a partir del cálculo del momento flector M, debido a la carga puntual P en el extremo de la viga que está dado por la ecuación (2):
En la ecuación (2), la x representa la longitud del vector posición, que se extiende desde el punto de aplicación de la fuerza al punto al cual se toma el momento (en este trabajo el momento se toma en la ubicación del sensor).
El momento M se puede obtener a partir de las ecuaciones de esfuerzo máximo y de la ley de Hooke [43], dadas por las ecuaciones (3) y (4), respectivamente.
La ecuación (3) describe el esfuerzo máximo en la viga, que ocurre en el punto de la sección transversal más alejado del eje neutro, justo donde se van a ubicar los sensores. La ley de Hooke, representada en la ecuación (4), muestra que el esfuerzo y la deformación registran una relación lineal en la zona elástica, entendiendo que esta zona elástica se presenta cuando las deformaciones son proporcionales al esfuerzo unitario y el material no se deforma permanentemente. Si se igualan las ecuaciones (3) y (4) y se despeja el momento de fuerza M, se obtiene la ecuación (5):
Donde E es el módulo de elasticidad del material, I es el momento de inercia, c es la distancia perpendicular del eje neutro al punto más alejado de este eje, o en otras palabras, es el mismo radio de la viga. La variable M es la deformación de la viga medida en la ubicación del sensor. Como cada sensor mide la variación de la longitud de onda central, entonces la deformación se obtiene mediante la ecuación (6).
Donde λc es la longitud de onda central de cada sensor y se usa como medida de referencia (sin deformación), λf es la longitud de onda desplazada por efecto de la deformación y k es la constante de deformación que está dada en µε/nm, por tanto, la deformación se mide en µε.
Una vez calculada la deformación en cada punto de sensado, entonces es posible estimar el momento de fuerza M y por consiguiente la fuerza P y el desplazamiento debido a la deflexión de la viga v A [42].
Materiales y métodos
En este título se describe la implementación de la red de sensores fotónicos propuesta como prototipo para el monitoreo de movimientos de tierra en masa. Se parte de la descripción del escenario en el que se instala la red de sensado, luego se presenta la implementación de los inclinómetros fotónicos y el sistema de interrogación usado para la captura de los datos provenientes de los sensores, y finalmente se describe la implementación de la topología de sensado conformada por un total de nueve inclinómetros.
Montaje del prototipo de perfil del suelo
El paso inicial para la implementación del prototipo de monitoreo de movimientos de tierra consistió en montar un escenario que representara la masa de tierra que se desea monitorear. A grandes rasgos, se buscó mostrar dos capas del suelo: una compacta y la otra porosa y quebradiza. Esto, debido a que, en un evento de movimiento de tierra, lo que se desplaza es el suelo superficial, que es poroso y quebradizo, sobre las capas de arcillas compactas. En la figura 5 se observa el prototipo por capas del escenario implementado.
Como se observa en la figura 5, se usaron dos placas de materiales: una de poliestireno que asemeja el suelo compacto sobre el que se empotran los inclinómetros y otra de poliuretano blando, que representa el suelo poroso superficial. Sobre esta última capa se aplicarán fuerzas que deformen el material en diferentes puntos con el fin de simular un movimiento de tierra.
Las dimensiones de cada placa son de 100x100x10 cm y las dos están colocadas sobre una base de madera que les da estabilidad a ambas y facilita el transporte del sistema.
Implementación de los inclinómetros fotónicos
Un inclinómetro fotónico consiste en una barra cilíndrica instrumentada con un par de sensores FBG ubicados a la misma altura, pero separados angularmente 90°, con el fin de medir deformaciones en los ejes cartesianos X y Y. En la figura 6 se muestra la representación gráfica de los inclinó-metros fotónicos implementados.
Se utilizó una barra de fibra de vidrio de 3 mm de diámetro y 30 cm de longitud. Este material es flexible y resistente, y se puede flexionar ampliamente, sin deformarse.
Los sensores FBG se instalaron a lo largo del eje longitudinal de las barras a una distancia de 15 cm desde la base y separados angularmente 90°, de modo que se pudieran medir deformaciones tanto en el eje X como en el eje Y. Los sensores utilizados son de fibra óptica monomodo estándar (Standar Single-Mode Fiber [SSMF]) solo recubierta por acrilato y con conectores FC-APC instalados en el laboratorio. Las longitudes de onda de los sensores varían entre 1515 y 1585 nm, con separación entre sensores de 5 nm.
Para fijar la fibra óptica a lo largo de la barra se utilizó un adhesivo de cianoacrilato y resina epóxica para proteger los puntos donde se empieza el pigtail del conector. En la figura 7 se observa un inclinómetro fotónico totalmente ensamblado.
Topología de la red de sensores fotónicos
Por lo general, las áreas en las que ocurren los movimientos de tierra en masa pueden variar desde algunos metros hasta varias hectáreas de terreno. En este sentido, en el prototipo implementado se seleccionó una topología en malla en la que se utilizan varios inclinómetros fotónicos para cubrir un área determinada. En total se instrumentaron e instalaron nueve inclinómetros, marcados con una letra en orden alfabético, tal como se aprecia en la figura 8. Sin embargo, el número de inclinómetros por utilizar en una aplicación real puede variar de acuerdo con el área de estudio.
Los nueve inclinómetros usados fueron instrumentados con dos sensores ópticos que entregan información de la deformación del inclinómetro en las direcciones X y Y. Estos sensores se identifican con la letra que representa al inclinómetro junto con un subíndice X o Y, de acuerdo con la dirección en la que se instaló. De esta manera, los sensores del inclinómetro 'A' se identifican como A x y A y . En la tabla 1 se presentan las longitudes de onda (λ) de los 18 sensores utilizados en la topología de sensado fotónico.
Tabla 1 Longitudes de onda (λ) de los sensores utilizados
| Sensor | λ(nm) | Sensor | λ(nm) |
|---|---|---|---|
| A x | 1515.087 | E y | 1519.992 |
| A y | 1515.173 | F x | 1515.545 |
| B x | 1520.067 | F y | 1575.221 |
| B y | 1524.822 | G x | 1520.040 |
| C x | 1515.659 | G y | 1525.073 |
| C y | 1575.468 | H x | 1555.057 |
| D x | 1519.872 | H y | 1575.044 |
| D y | 1525.094 | I x | 1549.785 |
| E x | 1525.272 | I y | 1539.994 |
Fuente: elaboración propia.
En la tabla 1 se advierte que varios sensores tienen la misma X, incluso los de un mismo inclinómetro, como se observa en el inclinómetro 'A'. Por tanto, se debe garantizar que los sensores con la misma λ no se mezclen por un mismo canal óptico. Este problema se resolvió fácilmente, dado que el sistema de interrogación utilizado proporciona cuatro canales independientes.
Por otro lado, se debe conocer la relación entre la deformación y el desplazamiento de la λ de los sensores, conocida como constante de deformación (k), que para el caso de las FBG utilizadas es de 804 µε/nm. Esto indica que por cada nanómetro que se desplace la λ central del sensor, la barra se deforma 804 microdeformaciones, justo en la ubicación del sensor.
Sistema de interrogación de los sensores fotónicos
El sistema de sensado fotónico implementado como prototipo para el monitoreo de movimientos de tierra en masa está conformado por la red de sensores descrita en la sección anterior, una caja de splitters ópticos, un interrogador de sensores ópticos de cuatro canales y un computador para el procesamiento de los datos, como se puede apreciar en la figura 9.
Los sensores FBG pueden medir la deformación en cada inclinómetro fotónico a partir de la variación en la longitud de onda de Bragg en la que están diseñados. Estas variaciones se pueden medir con un equipo conocido como interrogador óptico, que tiene la capacidad de interrogar cientos de sensores ópticos en tiempo real.
El mecanismo de interrogación consiste en utilizar un láser sintonizable, que realiza un escaneo en un determinado ancho de banda, a cierta frecuencia de barrido. Esta fuente de luz incide sobre la red de sensores ópticos en la que cada FBG refleja la longitud de onda de Bragg en la que fue diseñada. Luego, el interrogador óptico identifica las longitudes de onda reflejadas y proporciona información de cualquier variación que ocurra sobre estas. Adicionalmente, el interrogador cuenta con un software de adquisición y visualización, que permite exportar los datos capturados de los sensores para su posterior procesamiento.
En el prototipo implementado se utilizó un interrogador óptico sm130-700. El equipo cuenta con cuatro fuentes láser, que realizan un escaneo entre 1510 y 1590 nm a una frecuencia de 1 kHz. La resolución del equipo es de 1 pm, lo que le otorga la posibilidad de realizar medidas de 1 µε aproximadamente.
Cada salida del interrogador se conecta a una caja de splitters, formada internamente por cuatro splitters 1x8. Estos dispositivos permiten dividir las señales ópticas provenientes de los láseres para entregarlas a los 18 sensores. Las señales reflejadas por los sensores FBG se juntan nuevamente en los splitters, ya que en la dirección opuesta funcionan como combinadores ópticos. El interrogador recibe y procesa estas señales, generando un archivo de texto en el que guarda la información de las variaciones en longitud de onda de los 18 sensores. Finalmente, el archivo de texto generado es la base para el algoritmo que se describe en la siguiente sección.
Algoritmo de monitoreo de movimientos de tierra en masa
El algoritmo empleado se basa en el modelo analítico expresado en la sección introductoria, que consiste en la implementación de las ecuaciones de mecánica de materiales, para determinar los desplazamientos en los ejes X y Y de cada inclinó-metro fotónico a partir de la medida de deformación, que realiza cada sensor, en su respectivo eje.
En la figura 10 se muestra el diagrama de flujo del algoritmo analítico implementado. Una vez iniciado el programa, el primer paso es cargar los archivos (.txt o xvs) que genera el interrogador óptico en donde se guardan las variaciones en longitud de onda de cada sensor. Se generan dos archivos: uno sin ninguna alteración, para fijar las longitudes de onda de referencia (S10), y otro con las longitudes de onda de los sensores, luego de aplicar una carga en punto del prototipo (Su).
El tamaño de las matrices cargadas S10y S n es de 5000 filas por 18 columnas. Cada una registra la información de cada sensor, ordenado desde A x a I y . Cada fila es el valor de la longitud de onda muestreado en un instante de tiempo. Con el fin de simplificar el procesamiento se trabajó con el valor promedio de cada sensor, de tal modo que cada matriz se convirtió en un vector de longitudes de onda de una fila y 18 columnas.
Posteriormente se definen y calculan los parámetros conocidos como el radio de la viga r, el módulo de elasticidad de las vigas de fibra de vidrio E (este fue calculado en el laboratorio con la curva esfuerzo-deformación de una viga), la constante de deformación de los sensores k, el momento de inercia del área transversal I, la longitud de la viga desde el empotramiento L y la longitud desde el empotramiento al sensor Ls.
Luego de definir los parámetros conocidos, y teniendo los vectores de las longitudes de onda de referencia y desplazadas, se calcula el vector de deformaciones mediante la ecuación (6). Los siguientes pasos son calcular los vectores de momentos M, de fuerzas P y de desplazamientos v A mediante las ecuaciones (5), (2) y (1), respectivamente.
Hasta este punto se tiene un vector con la información de los desplazamientos en X y Y de cada inclinómetro fotónico. Estos valores se convierten en las coordenadas de un punto con el cual se traza un vector, que va desde la base de cada inclinómetro al respectivo punto encontrado. De modo que los vectores generados van a apuntar hacia el lugar donde se aplicó la carga, lo que equivale a identificar la dirección hacia donde está ocurriendo el movimiento de tierra.
Resultados y discusión
En este título del documento se presentan los resultados más relevantes obtenidos luego de la implementación de la red de sensores.
Conflictos en la alineación de los sensores
El primer paso en la implementación del prototipo de monitoreo de deslizamientos fue la instrumentación de los inclinómetros ya descrita. En este proceso se observó un problema en la alineación de cada sensor respecto al eje longitudinal correspondiente. Esto significa que, por ejemplo, un sensor en el eje X de un inclinómetro debe estar alineado exactamente sobre el eje; sin embargo, por las dimensiones de la barra utilizada y las del sensor resulta muy complejo garantizar una alineación exacta. Este fenómeno se aprecia en la figura 11.
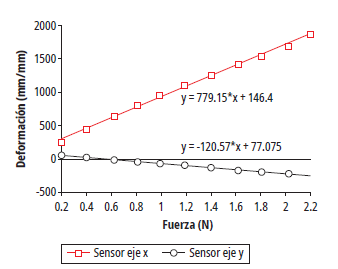
De esta forma, el desempeño de la red de sensores se ve limitado por un factor de precisión en la ubicación de los inclinómetros. El problema ilustrado en la figura 11 se logró soportar a partir de las curvas de fuerza contra deformación mostradas en las figuras 12 y 13. Las curvas de la figura 12 corresponden a las respuestas de los sensores tanto en el eje X (línea roja) como en Y (línea negra), cuando se aplican fuerzas en la dirección de X y asegurando que el sensor en esa dirección esté lo más alineado posible con el eje longitudinal. Por mecánica de materiales se esperaría que, si el sensor en el eje Y está perfectamente alineado con el eje, no haya deformación. Sin embargo, se observa que mientras el sensor en el eje X mide una deformación de 779.15 µε/nm, el sensor en el eje Y mide 120.57 µε/nm.
Fuente: elaboración propia.
Figura 12 Gráfica de fuerza contra deformación con el sensor del eje X alineado y la fuerza aplicada en la dirección X
Fuente: elaboración propia.
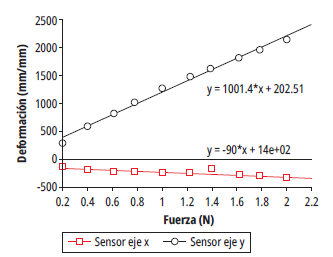
Figura 13 Gráfica de fuerza contra deformación con el sensor del eje Y alineado y la fuerza aplicada en la dirección Y
Por otro lado, las curvas mostradas en la figura 13 representan la respuesta de los sensores cuando se alinea el sensor del eje Y, con las fuerzas aplicadas en la dirección Y. Los resultados registran una pendiente de deformación de 1001.4 µε/nm en el eje Y, contra 90 µε/nm en el eje X. Esto revela que el sensor instalado en el eje Y tiene una mayor desviación respecto a su eje que el sensor en la dirección X.
Prueba de funcionamiento de la red de sensores
Una vez caracterizados los inclinómetros y teniendo clara la desviación de cada sensor con respecto al eje longitudinal, se realizó una prueba del funcionamiento del inclinómetro, consistente en la aplicación de fuerzas de una magnitud tal que pudiera deformar el inclinómetro en una dirección conocida. Posteriormente se recopiló la información de los sensores, mediante el sistema de interrogación, y se procesó con el algoritmo descrito.
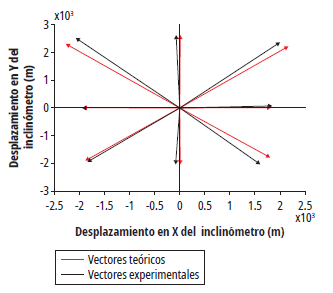
Como se observa en la figura 14, se aplicaron fuerzas en los ángulos de 0, 45, 90, 135, 180, 225, 270 y 315 grados. Las flechas negras representan los vectores obtenidos experimentalmente con un inclinómetro fotónico, mientras que las flechas rojas representan los vectores teóricos.
Fuente: elaboración propia.
Figura 14 Vectores de movimiento medidos experimentalmente por los inclinómetros fotónicos (negros) y teóricos (rojos)
El error obtenido para los ángulos definidos previamente fue relativamente bajo -cerca del 5 %- considerando que la implementación se realizó de forma manual, lo que representó un reto al manipular la red de sensores compuesta por inclinómetros de 2 mm.
Este error se midió en cada uno de los casos y se presentó en la tabla 2, donde se muestra que el error medido en los ángulos que concuerdan con la dirección de alguno de los ejes X y Y (0o, 90°, 180° y 270°) es menor que el error medido en las direcciones que no concuerdan con los ejes (45°, 135°, 225° y 315°). Esto se debe a que las fuerzas aplicadas en las direcciones de los ejes coinciden con la pequeña desviación en ese eje, de modo que solo se aprecia el efecto de la desviación del sensor en la otra dirección, mientras que en las direcciones que no concuerdan con los ejes se evidencia la sumatoria de desviaciones en ambas direcciones.
Adicionalmente, en la tabla 2 también se muestran los desplazamientos en X y Y medidos para cada uno de los ángulos estudiados, así como la magnitud de los vectores encontrados, los cuales se obtienen a partir de la medida de deformaciones realizada por cada sensor. Además, la magnitud de los vectores puede aportar información de la magnitud de la fuerza aplicada o del movimiento.
Tabla 2 Desplazamientos y ángulos medidos mediante un inclinómetro fotónico
| Ángulo teórico (°) | Ángulo experimental (°) | Error (°) | Desplazamiento eje X (mm) | Desplazamiento eje Y (mm) | Magnitud del vector (mm) |
|---|---|---|---|---|---|
| 0 | 2.140 | 2.140 | 1.872 | 0.069 | 1.874 |
| 45 | 49.742 | 4.742 | 2.027 | 2.394 | 3.137 |
| 90 | 91.468 | 1.468 | -0.067 | 2.635 | 2.636 |
| 135 | 129.702 | 5.297 | -2.090 | 2.517 | 3.271 |
| 180 | 180.420 | 0.420 | -1.974 | -0.014 | 1.974 |
| 225 | 226.339 | 1.339 | -1.865 | -1.955 | 2.702 |
| 270 | 267.698 | 2.301 | -0.082 | -2.041 | 2.043 |
| 315 | 308.651 | 6.348 | 1.619 | -2.025 | 2.593 |
Fuente: elaboración propia.
A pesar de la complejidad en la instrumentación de los inclinómetros fotónicos, dadas las dimensiones de la barra utilizada y las dimensiones de los sensores, en la tabla 2 se nota que el mayor error en los ángulos medidos es de 6.35° y el menor es de 0.42°. Estos resultados son alentadores, dado que al momento de implementar un inclinómetro a escala real, las dimensiones de la barra a utilizar son mayores (varios metros de longitud y varios centímetros de calibre), de tal modo que se puede garantizar una mayor precisión desde la instrumentación de los dispositivos.
Conclusiones
Se implementó un prototipo funcional de un sistema de monitoreo de movimientos de tierra en masa, mediante el uso de inclinómetros fotónicos que se basan en el empleo de sensores ópticos FBG, y de un algoritmo analítico de procesamiento con sustento en la teoría de mecánica de materiales.
El prototipo implementado tiene la capacidad de generar un vector en la dirección que ocurre el movimiento a partir de la información de la deformación que entregan los sensores FBG en cada eje de coordenadas X y Y de los inclinómetros.
Los resultados experimentales reflejan errores en la instrumentación de los sensores como se ilustra en la figura 11, debido a las dimensiones reducidas de cada inclinómetro y a que la instrumentación se realizó de forma manual. Sin embargo, a pesar de esto se lograron medidas en los ángulos de los vectores de movimiento con un error mínimo de 0.42°, máximo de 6.35° y un error medio de 3° sobre el total de medidas realizadas.
Los resultados son alentadores, pues en un inclinómetro a escala real, las dimensiones de la barra que se va a utilizar son mayores (varios metros de longitud y varios centímetros de calibre) permitiendo una mejor colocación de los inclinómetros. Además, apoyar la instrumentación con dispositivos o herramientas de precisión garantizaría una mejora significativa adicional en el desempeño del sistema de monitoreo, al lograrse un correcto posicionamiento de los sensores.
Aun así, con los bajos niveles de error obtenidos se demuestra que la red de sensores fotónicos propuesta es una herramienta prometedora para el monitoreo de deslizamientos de tierra orientado a la disminución de los efectos socioeconómicos que causan los desastres naturales.
Para trabajos futuros, en términos de software se recomienda el uso de técnicas de reconocimiento de patrones para optimizar el funcionamiento del sistema de monitoreo que emplea un método analítico. A su vez, se propone diseñar un algoritmo orientado a detectar no solo deformaciones puntuales en los inclinómetros, sino deformaciones distribuidas, como sucedería en un escenario de deslizamiento real.
Por último, se propone evaluar el desempeño de la red de sensores en un simulador físico de deslizamientos de suelo, para reforzar las pruebas con datos más contundentes. Para una etapa final, se plantea poner en marcha el sistema de monito-reo en un terreno real propenso a movimientos de tierra, lo cual permitiría evaluar el desempeño y la viabilidad de la red de sensores en una eventual incorporación a los procesos de prevención del riesgo, para disminuir los efectos de los desastres naturales.


























