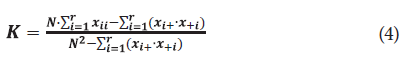Introducción
Existe una creciente demanda de mapas de uso y cobertura del suelo (LULC, por sus siglas en inglés) derivados de la investigación sobre el impacto del cambio climático, aplicaciones hidroecológicas y las intervenciones humanas en los ecosistemas [1]-[3]. El uso de la tierra (LU) se refiere a las acciones, que tienen lugar en la superficie, realizadas por los humanos como la urbanización o la industria; sin embargo, la cobertura terrestre (LC) se refiere a la descripción física de la superficie de la tierra como los bosques o cuerpos de agua [4]. Ambos conceptos son esenciales para comprender la dinámica del paisaje y su evolución temporal. Los mapas LULC desempeñan un papel fundamental en las políticas de planificación urbana, conservación y el monitoreo agrícola [5], [6].
Las imágenes capturadas por satelitales han adquirido un rol interesante para mapear el territorio debido a su amplia cobertura y eficiencia en términos de costos. El satélite Landsat-9 (L9) comenzó a operar desde finales del 2021, proporcionando imágenes multiespectrales de resolución moderada. Está equipado con un generador operativo de imágenes terrestres (OLI-2) y un sensor térmico infrarrojo (TIRS-2), que producen once bandas espectrales y resolución máxima de 15 m, con frecuencia periódica de 16 días [7]. Estas imágenes han ganado una considerable atención en la investigación gracias a su acceso libre y cobertura global [8].
La clasificación de imágenes en teledetección representa el método más común para identificar tipos de cobertura terrestre. En la última década, los algoritmos de aprendizaje automático (ML) se han utilizado con efectividad para la producción de mapas LULC debido a su capacidad de aumento de calidad, eficiencia y escalabilidad en comparación con los modelos tradicionales basados en discriminación de píxeles [9]. Estos algoritmos se pueden categorizar en paramétricos y no paramétricos según si es necesario o no hacer suposiciones específicas sobre la distribución de sus datos [10]. Los clasificadores paramétricos, como la regresión logística y el Naive Bayes (NB), son recomendados cuando se establecen relaciones lógicas claras y los datos se ajustan a los supuestos paramétricos subyacentes. Por otro lado, los clasificadores no paramétricos pueden adaptarse a relaciones no lineales complejas, que los hacen más adecuados para la clasificación de coberturas terrestres [11]. Según diversos estudios, los clasificadores no paramétricos más empleados en LULC son Random Forest (RF), k-Nearest Neighbor (KNN), Support Vector Machines (SVM) y Classification And Regression Trees (CART) [12]-[14]. De acuerdo con Ouma et al. [15], al comparar algoritmos como CART, RF, Gradient Tree Boosting (GTB) y SVM, la precisión del clasificador depende de la clase mapeada. El suelo desnudo se representa mejor utilizando RF y CART con una precisión del 98 % mientras que SVM y GTB fueron los más adecuados para cuerpos de agua. Los clasificadores de mejor rendimiento paras las cubiertas vegetales fueron RF, SVM y GTB. Por su parte, Deng et al. [16] señalan que la precisión de la clasificación de LULC está fuertemente influenciada por características del sensor y factores relacionados con los datos de la imagen, como la resolución espacial y temporal, además del software y hardware de procesamiento.
Los modelos de clasificación automática se basan en la obtención de firmas espectrales de clases predefinidas mediante datos de entrenamiento. Estos modelos se centran en diferenciar píxeles que corresponden a diferentes tipos de cobertura [17]. El análisis de imágenes basado en objetos (OBIA) ha superado a los métodos que se basan en la discriminación de píxeles al ofrecer una representación más precisa de la distribución de la cobertura del suelo [11].
La segmentación constituye el fundamento del modelo OBIA, la cual transforma datos complejos en unidades significativas. Los objetos segmentados proporcionan una representación más cercana a cómo los seres humanos perciben el mundo real. La segmentación implica dividir las imágenes en conjuntos de objetos espacialmente contiguos, donde cada uno está formado por un grupo de píxeles vecinos con homogeneidad o significado semántico [18].
Para lograr una buena precisión en la clasificación LULC, es esencial contar con conjuntos de datos de entrenamiento suficientemente amplios.
Sin embargo, surge un problema debido a que las diversas coberturas ocupan proporciones de área diferentes, lo que significa que algunos de estos conjuntos de datos son adecuados en tamaño mientras que otros resultan ser limitados [19].
Se han llevado a cabo varios estudios con el objetivo de encontrar el algoritmo de clasificación ideal para la creación de mapas LULC. Estos estudios implican comparar el rendimiento del algoritmo consigo mismo y en relación con otros métodos de clasificación; sin embargo, las conclusiones varían considerablemente [20], [21]. Yuh et al. [22] sostienen que los algoritmos ML se pueden entrenar utilizando conjuntos de datos equilibrados (con el mismo número de píxeles muestreados por clase) y desequilibrados (con diferente número de píxeles muestreados para cada clase) sin grandes incertidumbres de clasificación. Por otro lado, Azadbakht et al. [23] han indicado que los conjuntos de datos desequilibrados pueden plantear desafíos para los algoritmos de ML, especialmente en la categorización de las clases menos frecuentes. Esto sugiere que los conjuntos de datos desequilibrados todavía presentan desafíos significativos que deben abordarse adecuadamente en el entrenamiento de algoritmos ML. Existe poca investigación que compare RF y SVM en el contexto de imágenes Land-sat-9, especialmente en Colombia. Si bien el diseño de muestreo está bien documentado en la literatura, quedan dudas sobre el número y tamaño de muestras requeridas, su calidad y el desequilibrio de clases.
Este estudio se centra en la evaluación de dos algoritmos ampliamente utilizados en la clasificación LULC: Support Vector Machine (SVM) y Random Forest (RF) (referido como Random Trees (RT) en ArcGIS Pro). Estos algoritmos se seleccionaron debido a su capacidad para clasificar imágenes con robustez y abordar desafíos como el ruido y el sobreajuste. El objetivo de esta investigación es analizar cómo las fluctuaciones en la dimensión del grupo de entrenamiento (equilibrados y desequilibrados) influyen en la eficiencia de los algoritmos de aprendizaje automático supervisado bajo un modelo de segmentación OBIA. Este enfoque destaca la relevancia de la ingeniería geomática en la aplicación efectiva de modelos de clasificación de imágenes satelitales como SVM y RF en el ámbito de la teledetección. Estas técnicas son aplicables en el análisis multitemporal de LULC para la cartografía de diagnóstico en el ordenamiento territorial.
Materiales y métodos
Área de estudio
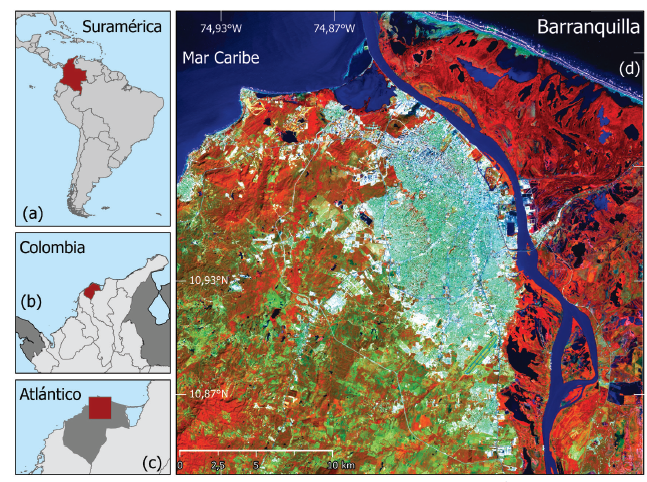
Con el objetivo de comparar el desempeño de los dos clasificadores mediante distintas estrategias para la obtención de las muestras de entrenamiento, se seleccionó una zona de 30 x 30 km en el Área Metropolitana de Barranquilla (AMB). Esta área está delimitada por las latitudes 10,82° N y 11,09° N, así como las longitudes 74,68° W y 74,96° W. Según informes oficiales, Barranquilla cuenta con una población de 2,7 millones de habitantes y se clasifica como la cuarta área metropolitana más grande de Colombia [24]. La ciudad se encuentra en el delta del río Magdalena, en la costa del mar Caribe (figura 1). Este río, que atraviesa Colombia de sur a norte, es considerado la principal arteria fluvial de la nación. Barranquilla es el epicentro del AMB y la principal ciudad del caribe colombiano, tanto en términos demográficos como económicos [25]. Los principales ecosistemas naturales en el área de estudio son el bosque tropical seco, el río Magdalena y los manglares estuarinos [26]. El uso del suelo es principalmente urbano y de conservación forestal. Por sus fronteras naturales, el crecimiento del AMB está restringido al suroeste de Barranquilla.
Datos
En este estudio, se utilizó una imagen satelital de la Tierra capturada por el instrumento OLI-2 a bordo del satélite L9, adquirida el 6 de enero del 2022. Este instrumento proporciona imágenes multiespectrales con una resolución espacial de 30 m, que abarcan cinco bandas visibles e infrarrojas cercanas (VNIR), dos bandas infrarrojas de onda corta (SWIR) y una banda cirrus, con una frecuencia de captura de datos cada 16 días. Además, L9 ofrece una banda pancromática de 15 m, que implica fusionar su información de alta resolución espacial con las bandas multiespectrales (que tienen mayor información espectral). Esta fusión permite crear imágenes compuestas con una alta resolución espacial y una información espectral detallada, que favorece la detección de características LULC más finas [27]. Esta técnica mejora significativamente la calidad del conjunto de datos procesados al combinar las bandas espectrales con un nivel de detalle superior.
La imagen se obtuvo del sitio web EarthExplorer del Servicio Geológico de los Estados Unidos (USGS) disponible en https://earthexplorer.usgs.gov/. La ruta y la fila de la imagen descargada fueron 009 y 052. Cada producto Landsat se entrega con bandas espectrales separadas en formato Geo-TIFF y está georrefferenciado al datum WGS84 en la proyección cartográfica UTM (18N). Las bandas utilizadas en este estudio incluyeron la banda 2 (0,45-0,51 µm), banda 3 (0,53-0,59 µm), banda 4 (0,64-0,67 um), banda 5 (0,85-0,88 um), banda 6 (1,57-1,65 µm), banda 7 (2,11-2,29 um) y la banda 8 (0,53-0,68 um). En el procesamiento de la imagen se emplearon los softwares ENVI 5.3 y ArcGIS Pro 2.8.0.
Métodos
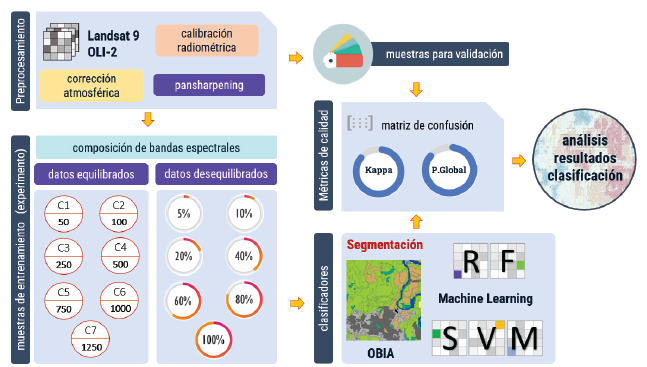
La metodología propuesta está compuesta por cuatro etapas: (1) calibración de datos, (2) esquema de clasificación y áreas de entrenamiento, (3) segmentación y algoritmos de clasificación y (4) métricas de calidad. La figura 2 describe el flujo de datos aplicado en este experimento.
Calibración de datos
La calibración radiométrica, que transformó los valores registrados por el sensor a unidades de radiancia aparente, se realizó siguiendo el procedimiento ampliamente descrito en el trabajo de Chander et al. [28]. Posteriormente, la imagen fue corregida por efectos atmosféricos para minimizar los errores causados por la dispersión y absorción de radiación debido al vapor de agua, partículas de polvo y aerosoles. Se empleó el método de substracción de objetos oscuros (DOS1) basado en el supuesto de que objetos oscuros como sombras, agua o bosques densos tienen una reflectancia cercana a cero, es decir, menor o igual al 1 %. Bajo esta suposición, los píxeles que representan estas características se consideran objetos oscuros y se utilizan para identificar la dispersión atmosférica [29]. Este método de corrección ha sido ampliamente utilizado en estudios previos de LULC [30], [31]. El procedimiento se aplicó empleando la calculadora ráster de ArcGIS Pro 2.8.0. La reflectancia de la superficie (p)se calculó mediante la siguiente expresión:
donde L λ es la radiancia espectral medida por el sensor, L p es la radiancia de la atmósfera (efecto bruma), d es la distancia Tierra-Sol en unidades astronómicas, ESUN λ es la irradiancia solar exoatmosférica y θ S es el ángulo centital solar. El efecto bruma L p está definido así:
donde L min es el valor mínimo de radiancia en la imagen, que se asume como radiancia del objeto oscuro en la sombra total y L D01% ) es el valor de radiancia correspondiente al 1 % de reflectancia, utilizado para identificar los píxeles oscuros en la imagen [32].
Finalmente, todas las bandas se recortaron para ajustarse a los límites del área de estudio.
Esquema de clasificación y áreas de entrenamiento
En este estudio las características superficiales terrestres fueron clasificadas en siete cubiertas referidas en el modelo Corine Land Cover (CLC) para Colombia. Estas son agua continental, agua marítima, tejido urbano, pastos limpios, mosaico de cultivos, bosque y red vial.
Se empleó un método de muestreo aleatorio simple para elegir las muestras del conjunto de datos tanto de entrenamiento como de validación, que busca asegurar la representación adecuada de las clases minoritarias [33].
Se seleccionaron cien segmentos para cada tipo de cobertura y se calculó la cantidad de píxeles en cada uno, como se indica en la tabla 1. Posteriormente, se calculó un número específico de píxeles para validar utilizando la ecuación de muestreo estratificado para poblaciones finitas propuesta en el estudio de Foody [34].
Tabla 1 Tamaños de muestras de entrenamiento y validación
| Clase LULC | Definición | Entrenamiento (segmentos/ píxel) | Validación (píxeles) |
|---|---|---|---|
| Agua continental | Incluye masas de agua dulce, laguna costera, humedal, lagos y ciénagas. | 100/ 71.190 | 383 |
| Agua marítima | Se refiere a las masas de agua salada que cubren los mares, bahías y zonas como manglares. | 100/ 101.575 | 384 |
| Tejido urbano | Edificaciones y estructuras artificiales continuas y discontinuas creadas por el ser humano. | 100/26.898 | 380 |
| Pastos limpios | Áreas de cultivo de pasto para alimentación del ganado, incluye pastos arbolados, pastos enmalezados y praderas. | 100/19.136 | 378 |
| Mosaico de cultivos | Áreas de amplia variedad de cultivos agrícolas. | 100/9.281 | 370 |
| Bosque | Áreas cubiertas densamente por árboles perennes de gran altura. | 100/16.569 | 376 |
| Red vial | Áreas destinadas a infraestructuras de carreteras y redes de transporte. | 100/2.411 | 332 |
Fuente: elaboración propia.
Posteriormente, los polígonos de entrenamiento de cada clase se dividieron en dos grupos: muestras equilibradas y muestras desequilibradas. En las muestras equilibradas, cada clase tuvo una cantidad similar de muestras de entrenamiento, que garantizó que todas las clases estuviesen representadas de manera equitativa en el conjunto de datos. En contraste, las muestras desequilibradas permitieron que algunas clases tuviesen más muestras de entrenamiento que otras, lo cual refleja la proporción original de píxeles en la estratificación inicial. Los datos de las muestras de entrenamiento se dividieron en catorce conjuntos, siete equilibrados y siete desequilibrados de acuerdo con las cantidades expresadas en la tabla 2. Este enfoque adaptado de Thanh Noi y Kappas [35] permitió evaluar cómo el equilibrio de clases afectó el rendimiento de los algoritmos de clasificación en comparación con las muestras desequilibradas.
Tabla 2 Muestreo de datos para entrenar los clasificadores
| Equilibrados | C1_e | C2 e | C3 e | C4_e | C5 e | C6 e | C7 e |
|---|---|---|---|---|---|---|---|
| Núm. píxeles | 50 | 100 | 250 | 500 | 750 | 1000 | 1250 |
| Desequilibrados | C1_d | C2_d | C3_d | C4_d | C5_d | C6_d | C7_d |
| Núm. píxeles | 5 % | 10 % | 20 % | 40 % | 60 % | 80 % | 100 % |
Nota. C1_e: conjunto 1 equilibrado; C1_d: conjunto 1 desequilibrado
Fuente: elaboración propia.
Segmentación y algoritmos de clasificación
La meta de la clasificación supervisada es asignar cada píxel de la imagen a clases particulares de cobertura del suelo. En este proceso, se utilizaron los algoritmos de Random Trees (RT) y Support Vector Machine (SVM) disponibles en ArcGIS Pro. El proceso de segmentación en ArcGIS Pro se fundamenta en el modelo Mean Shift. Este modelo emplea el reconocimiento de patrones a través de una ventana móvil para calcular valores promedio de píxeles, agrupándolos en segmentos. Una descripción detallada de Mean Shift se encuentra en Comaniciu y Meer [36]. Bajo el enfoque OBIA se categorizaron los segmentos constituidos por agrupaciones de píxeles con tipologías afines. Las características de los segmentos están determinadas por tres parámetros: detalle espectral, detalle espacial y tamaño mínimo del segmento. Debido a la falta de parámetros de referencia establecidos, se utilizó el método de prueba y error para encontrar la escala de segmentación adecuada [37]. En este estudio, se emplearon los siguientes valores para configurar los parámetros: detalle espectral: 20, detalle espacial: 20 y tamaño mínimo del segmento en píxeles: 15. En general, se buscó fragmentar la imagen en un número finito de regiones con la mayor escala posible, pero al mismo tiempo, asegurar la capacidad de distinguir entre ellas de manera efectiva. Estos segmentos fueron utilizados como muestras de entrenamiento en las que se probaron diversas combinaciones de bandas espectrales para lograr una mejor diferenciación de coberturas.
Support Vector Machine (SVM) se destaca como un algoritmo de aprendizaje automático supervisado de gran eficiencia en la segmentación de datos lineales y no lineales en el ámbito de los sensores remotos [38], [39]. Este modelo opera bajo la teoría del aprendizaje estadístico y la función de núcleo (Kernel). Su objetivo es encontrar de manera iterativa un hiperplano que maximice el margen libre de datos entre las clases de entrenamiento. El término "hiperplano" representa una regla de decisión lineal que emplea una función de mapeo derivada de las muestras de entrenamiento, que busca minimizar las clasificaciones erróneas [40]. Los puntos más cercanos al margen de clasificación se conocen como vectores de soporte. Luego, el modelo evalúa la estimación del hiperplano y hace predicciones con los datos de prueba. Si las predicciones son incorrectas, se produce una nueva selección de los vectores de soporte y se ajusta un nuevo hiperplano para mejorar la calidad del modelo. Las funciones de núcleo de base polinómica y radial se utilizan a menudo para proyectar clases no lineales en clases lineales separables en una dimensión superior [41]. Para llevar a cabo el experimento, se suministraron al clasificador SVM la imagen segmentada, las muestras de entrenamiento y el esquema de clasificación. En ArcGIS Pro 2.8.0 solo es posible ajustar un parámetro dentro del modelo: la cantidad máxima de muestras por clase, que está limitada a 500. Este valor se mantuvo en su configuración predeterminada, luego, todas estas entradas se utilizaron conjuntamente para entrenar el clasificador SVM. La implementación de este algoritmo produjo un total de catorce modelos de clasificación SVM, divididos en siete para conjuntos de datos equilibrados y otros siete para conjuntos desequilibrados.
En ArcGIS Pro, el algoritmo Random Trees (RT) es un método de clasificación supervisado. Está fundamentado en el método estadístico de Random Forest (RF) [42]. Este emplea múltiples árboles de decisión integrados mediante la técnica de agregación Bootstrap, lo que implica entrenar cada árbol con diferentes subconjuntos de datos para obtener una clasificación similar. Al combinar los resultados de estos árboles, se compensan errores, lo que resulta en una decisión final basada en los votos de los árboles individuales. La característica destacada de este método es su habilidad para prevenir el sobreajuste del conjunto de entrenamiento, además de su eficiencia en el tiempo de clasificación [43]. El clasificador RT fue entrenado con el número máximo de árboles en 50 y su profundidad máxima en 30. Estos son los valores predeterminados sugeridos por ArcGIS Pro, que han sido probados también con resultados estables en un estudio de Wessel et al. [44]. Con esta configuración, se generaron catorce modelos de clasificación RT, distribuidos en siete conjuntos equilibrados y siete desequilibrados.
Métricas de calidad
Para evaluar el rendimiento de los clasificadores, se recolectaron muestras adicionales de segmentos en áreas distintas a las utilizadas para el entrenamiento. Cada segmento de muestra se asoció a una clase específica LULC mediante una imagen de Google Maps. Estas muestras se emplearon para realizar la evaluación cuantitativa de los clasificadores a partir del cálculo de matrices de confusión. Con ello se calculó la precisión global (OA), que ofrece una medida general de qué tan bien el clasificador ha asignado de manera correcta las clases en relación con todas las muestras de validación [45]. Así mismo, el coeficiente Kappa (K) fue calculado para evaluar la concordancia entre las clasificaciones observadas y las predicciones hechas por el clasificador, teniendo en cuenta las coincidencias que no podrían deberse al azar. Cuanto más cercano a 1 sea el valor de Kappa, mejor es el rendimiento del clasificador, lo que indica una alta concordancia entre las clasificaciones y las observaciones reales. El coeficiente Kappa (K) y la precisión global (OA) se calcularon a partir de las siguientes ecuaciones:
donde x ii es el número de muestras clasificadas correctamente, N es el total de muestras extraídas y r es el número total de clases.
x i+ es el número total de muestras clasificadas en la clase i, x +i es el número total de muestras de la clase t en las muestras de referencia.
Resultados
Rendimiento de los clasificadores SVM y RT en conjuntos de datos equilibrados
Este estudio analizó el desempeño de dos modelos de aprendizaje automático en la clasificación LULC basada en objetos utilizando una imagen L9 OLI-2. La figura 3 muestra la precisión general (OA) de los algoritmos evaluados en relación con el tamaño de la muestra para grupos equilibrados. En general, se observó un aumento en la precisión de ambos clasificadores a medida que aumentó la cantidad de píxeles de entrenamiento para la clasificación. Ambos métodos de clasificación mostraron su mayor precisión al emplear conjuntos de 1250 muestras mientras que la precisión más baja se registró con conjuntos de 50 muestras. Sin embargo, cada clasificador respondió de manera diferente al aumento del tamaño de la muestra. La clasificación de SVM alcanzó una precisión general del 64 % a partir de conjuntos con 750 muestras, aunque, la estabilidad de este clasificador parece lograrse a partir de 500 muestras con una precisión global de 62 %. Desde 100 a 1000 muestras, el clasificador RT presentó un comportamiento casi lineal de incremento continuo, pero, con un crecimiento porcentual bajo del 7 %. No obstante, alcanzó su máxima precisión de 68 % con 1250 muestras que superan en 4 puntos porcentuales a SVM.
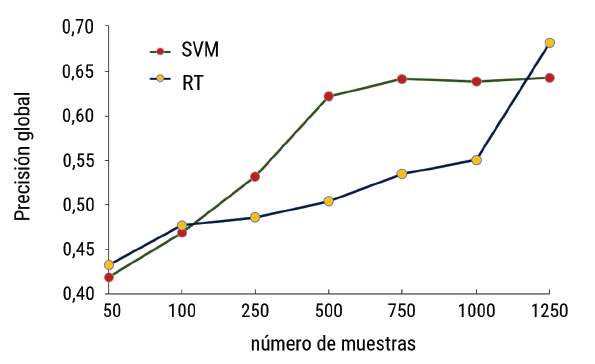
Fuente: elaboración propia.
Figura 3 Precisión global de las clasificaciones supervisadas y el tamaño del conjunto de entrenamiento en datos equilibrados
Las gráficas de violín en la figura 4 ilustran la distribución individual de los datos muestreados para cada clasificador y el número de píxeles seleccionado. La caja representa el rango intercuartílico (IQR) del conjunto de datos, es decir, el rango que contiene el 50 % central de los datos. El punto de color rojo indica la media, mientras que la línea en el interior de la caja representa la mediana.
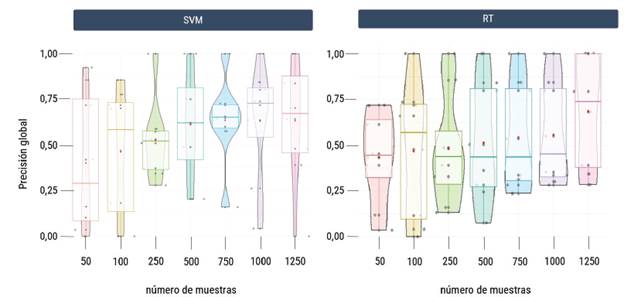
Fuente: elaboración propia.
Figura 4 Dispersión de datos muestrales de los clasificadores evaluados bajo conjuntos equilibrados
Aunque la precisión de ambos clasificadores aumentó con la cantidad de píxeles de entrenamiento utilizados para la clasificación, la amplia variabilidad en las cajas IQR, especialmente para RT en comparación con SVM, indicó que hay una gran dispersión en los datos de entrenamiento. Esta variabilidad en RT sugiere inestabilidad en el rendimiento del modelo y la incapacidad para mejorar de manera consistente su precisión global, especialmente en comparación con SVM. La sensibilidad de RT a las variaciones en los datos de entrenamiento pudo conducir a resultados poco consistentes incluso cuando se utilizaron más datos para el entrenamiento, como se observa entre las 250 y 1000 muestras. Por otro lado, la menor variabilidad en SVM indicó una mayor estabilidad en el rendimiento del modelo, lo que sugiere que SVM fue capaz de manejar las variaciones en los datos de entrenamiento y producir resultados más consistentes con el aumento del tamaño del conjunto de entrenamiento.
Rendimiento de los clasificadores SVM y RT en conjuntos de datos desequilibrados
En la figura 5 se presenta el desempeño de los clasificadores con datos desequilibrados, evaluado mediante la precisión global (OA). En todos los niveles de remuestreo, se observó que SVM siempre produjo resultados de mayor precisión en comparación con RT. Sin embargo, las tres precisiones más altas obtenidas por ambos clasificadores variaron ligeramente entre sí. Los resultados de precisión del SVM no alcanzaron diferencias significativas entre los tamaños de muestra de entrenamiento del 60 %, 80 % y 100 % con valores de 0,84, 0,84 y 0,86 respectivamente. Por su parte, RT alcanzó valores de 0,78, 0,79 y 0,81 sobre el mismo muestreo. En los conjuntos de entrenamiento del clasificador SVM se evidenció un comportamiento casi lineal entre los tamaños de muestra del 10 % al 100 %. Esto significa que, al incrementar la cantidad de muestras de entrenamiento, el rendimiento del modelo mejora de manera predecible y constante. A través del comportamiento general de SVM, se interpreta que con un tamaño de muestra del 60 % se obtienen resultados consistentes de alta precisión, lo que indica que no es necesario aumentar el tamaño de las muestras para mantener un rendimiento óptimo.
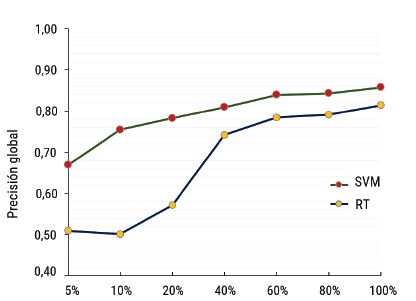
Fuente: elaboración propia.
Figura 5 Precisión global de las clasificaciones supervisadas y el tamaño del conjunto de entrenamiento en datos desequilibrados
La precisión del RT mostró diferencias significativas entre tamaños de muestra pequeños del 10 %, 20 % y 40 %. Se observó un aumento de 7 puntos porcentuales del 10 % al 20 % y un incremento de 17 puntos porcentuales entre el 20 % y 40 %, esto señala un aumento significativo en la precisión del modelo. Dicho aumento sugiere que el modelo logró aprender patrones más precisos entre el 20 % y el 40 % de las muestras de entrenamiento desequilibradas. A partir del 40 %, la figura mostró un comportamiento lineal con un aumento progresivo constante a medida que el tamaño de la muestra aumentó. Sin embargo, en las muestras del 60 %, 80 % y 100 % no se observó un aumento significativo, ya que sus precisiones fueron 0,78, 0,78 y 0,81 respectivamente. Esto indica que se alcanzó un punto de estabilidad en la precisión del algoritmo después de utilizar el 60 % de los datos de entrenamiento. A pesar de aumentar el tamaño de la muestra al 80 % y 100 %, la precisión se mantuvo en un nivel similar, lo que indica que no hubo mejoras significativas en la precisión del modelo con tamaños de muestra más grandes. Además, esto se interpreta como que el modelo RT logró su capacidad máxima de aprendizaje con el 60 % de los datos de entrenamiento empleados.
La figura 6 ilustra la distribución individual de los datos muestreados para cada clasificador y porcentaje de muestra mediante gráficas de violín. Resulta notable que en el muestreo del 5 % de los datos de SVM hubo una alta densidad alrededor de la media. Esto indica que espectralmente las muestras tuvieron valores cercanos entre sí, lo cual no es representativo de la población general y se evidenció a través del menor grado de precisión general obtenido. Las distribuciones de datos del 60 %, 80 % y 100 % presentaron un tamaño cercano al cuerpo del violín, lo cual indica homogeneidad en sus distribuciones y sugiere estabilidad en el rendimiento del modelo SVM. Las cajas del rango intercuartílico (IQR) del clasificador RT fueron significativamente más alargadas en comparación con las de SVM. La menor variabilidad en las predicciones del clasificador SVM, evidenciada por las cajas del IQR más cortas, señala una consistencia sobresaliente en las predicciones de este modelo. Ambos clasificadores parecen ser buenos generalizadores, ya que diferentes conjuntos de entrenamiento del mismo tamaño produjeron precisiones similares.
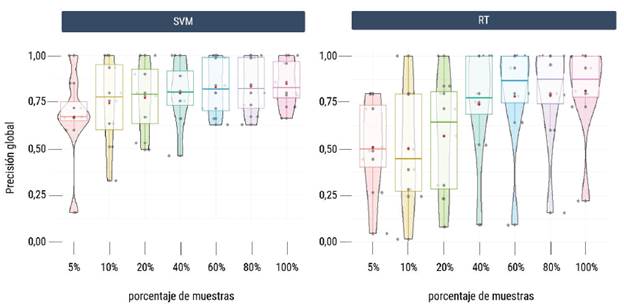
Fuente: elaboración propia.
Figura 6 Dispersión de datos muestrales de los clasificadores evaluados en conjunto de datos de entrenamiento desequilibrados
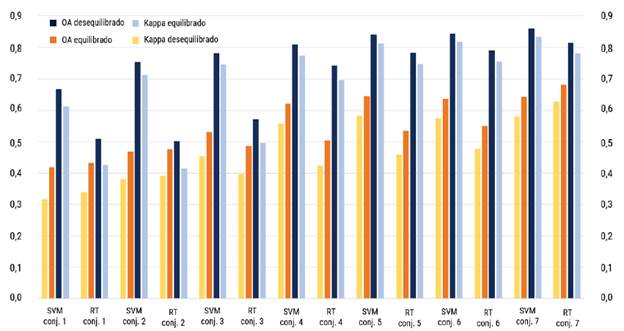
La figura 7 presenta el contraste de las diferencias obtenidas entre los conjuntos de datos equilibrados y desequilibrados de los catorce tamaños de muestra de entrenamiento para los clasificadores evaluados.
Discusión
En todos los casos, los valores del coeficiente Kappa (K) se encontraron cercanos a la precisión general. Esta cercanía indicó que las clasificaciones fueron consistentes, respaldando la calidad de los modelos y su capacidad para predecir con precisión las categorías sin depender del azar. Los conjuntos de entrenamiento desequilibrados (que muestrearon las clases en proporciones diferentes) mostraron una notable superioridad en precisión en comparación con los conjuntos equilibrados, donde por cada clase se muestreó la misma cantidad de píxeles que para las otras. Esto destaca la mayor capacidad de los clasificadores para aprender y predecir de manera más efectiva cuando se entrenan con datos desequilibrados. Los hallazgos mencionados destacan que los conjuntos de entrenamiento desequilibrados lograron capturar de manera más precisa la realidad del paisaje al reflejar las proporciones reales de las clases. En contraste con estos resultados, Thanh Noi y Kappas [35] argumentan que el rendimiento de los clasificadores en subconjuntos de datos equilibrados y desequilibrados fue comparable cuando el tamaño del conjunto de entrenamiento era convenientemente grande. Aunque los algoritmos y las técnicas de manejo del desequilibrio fueron equivalentes, los conjuntos de datos pudieron tener variaciones sutiles asociadas a la distribución y características de las clases. Otro factor que pudo influenciar estos resultados contradictorios fue la configuración de los parámetros del modelo SVM y RF.
En el caso de SVM, la función de penalización (C) y el valor de gamma (Y) son los dos parámetros esenciales que controlan el rendimiento de SVM cuando se utiliza la función de base radial (RBF) como núcleo central [46]. El parámetro de costo (C) controla el equilibrio entre la precisión de la clasificación y la simplicidad del modelo, mientras que el parámetro gamma (Y) regula la flexibilidad del límite de decisión en el modelo [47]. Thanh Noi y Kappas [35] realizaron pruebas con 10 valores para C y 7 hasta encontrar su combinación óptima. Sin embargo, estos parámetros no están disponibles para la calibración del modelo SVM en ArcGIS Pro.
Nuestro estudio se suma al debate sobre el rendimiento del clasificador RF en diferentes tamaños de conjuntos de entrenamiento. RT siempre presentó mayor precisión general sobre su rendimiento en datos desequilibrados que sobre los equilibrados. Este resultado respalda los hallazgos presentados por Mellor et al. [48] que señalaron que cuanto mayor fue el área de la clase de cobertura terrestre en el conjunto de datos, se necesitaron más muestras de entrenamiento para lograr una mejor precisión del clasificador. Por el contrario, Ramezan et al. [49] sostienen que RF es resistente a la variación en el tamaño de las muestras de entrenamiento, manteniendo una alta precisión, incluso con tamaños de muestra pequeños, y mostrando una disminución mínima en la precisión general a medida que aumentó el volumen de las muestras de entrenamiento. Resultados que fueron obtenidos con una configuración de número máximo de árboles en 500 mientras que en nuestro trabajo este parámetro fue de 50. Entrenar el clasificador RT con 50 árboles pudo limitar la capacidad del modelo para capturar la complejidad de los datos, especialmente cuando se enfrentó a tamaños pequeños de muestra.
Por otro lado, el estudio de Ramezan et al. [49], que utilizó 500 árboles, podría haber permitido que su modelo aprendiera patrones más sutiles y se adaptara mejor a los tamaños variados de muestra. Entrenar un clasificador RF con un número mayor de árboles aumenta generalmente la capacidad del modelo para aprender patrones complejos en los datos, lo que puede llevar a una mejor generalización. Sin embargo, después de un cierto punto, el beneficio de agregar más árboles disminuye y puede volverse computacionalmente costoso [50].
En este sentido, nuestros datos reportaron que RT en los conjuntos 5, 6 y 7 de la figura 7 (muestreos de 60 %, 80 % y 100 %) no presentaron diferencias significativas frente a la OA. Esto podría implicar que el modelo alcanzó su capacidad máxima de aprendizaje con el 60 % de los datos y agregar más datos no resultó en un aumento importante de su precisión general. A pesar de que se presentaron diferencias en el rendimiento entre conjuntos de datos de entrenamiento equilibrados y desequilibrados para ambos algoritmos, la precisión demostró ser consistentemente superior en el caso de SVM en comparación con RT. La homogeneidad tanto en las muestras de entrenamiento como en las de validación se identificó como un factor crítico para la estabilidad en el rendimiento de los modelos, esta tendencia estuvo respaldada por la precisión global (OA) y el índice Kappa.
El rendimiento del modelo SVM se estabilizó al emplear el 60 % del tamaño total de las muestras de datos de entrenamiento. Aumentar el tamaño de las muestras más allá de este punto no proporcionó mejoras significativas en la precisión del modelo. La tabla 3 presenta la superficie ocupada por las clases LULC, así como el área ocupada por las regiones de entrenamiento. Además, muestra el porcentaje que estas áreas representan en relación con el área total clasificada. También se detalla la precisión del usuario para cada clase correspondiente al modelo SVM con un 60 % del tamaño total de las muestras de datos de entrenamiento.
Tabla 3 Resultados de precisión de usuario para clases LULC (SVM, 60 % muestras de entrenamiento)
| Clase LULC | Área clasificada (km2) | Área de entrenamiento (km2) | % área de entrenamiento sobre el área clasificada | Precisión de usuario |
|---|---|---|---|---|
| Agua continental | 120 | 9,7 | 8,1 | 1,0 |
| Red vial | 12 | 0,3 | 2,6 | 1,0 |
| Bosques | 280 | 2,3 | 0,8 | 0,98 |
| Pastos limpios | 112 | 2,6 | 2,3 | 0,91 |
| Agua marítima | 127 | 13,9 | 10,9 | 0,85 |
| Tejido urbano | 151 | 3,7 | 2,4 | 0,69 |
| Mosaico de cultivos | 98 | 1,3 | 1,3 | 0,66 |
Fuente: elaboración propia.
La variación de los porcentajes del área de entrenamiento entre las cubiertas de agua continental (8,1 %), red vial (2,6 %) y bosques (0,8 %), todas con una precisión de usuario muy alta, resulta interesante y puede atribuirse a la complejidad inherente de estas clases. Es posible que existan variaciones naturales significativas en las características del agua, como profundidad, turbulencia y características del lecho, que requieren un área de entrenamiento más grande para capturar estas variaciones. Por otro lado, las características de las carreteras, como color, textura y forma, podrían ser más homogéneas y fáciles de aprender para el modelo, lo que explicaría por qué se necesita un área de entrenamiento menor. La clase bosque, a pesar de tener un porcentaje de área de entrenamiento baja, logró una alta precisión de usuario del 98 %. Las áreas de bosque a menudo presentan una mayor heterogeneidad espacial, lo que puede proporcionar una gama más amplia de firmas espectrales en un área relativamente pequeña, permitiendo así un mejor aprendizaje con menos datos de entrenamiento. El tejido urbano y los mosaicos de cultivos pueden ser muy heterogéneos en términos de estructuras, patrones y materiales. En áreas urbanas hay una gran variabilidad en materiales y tipologías constructivas. De manera similar, los mosaicos de cultivos pueden incluir diferentes tipos de cultivos con características espectrales disímiles. Estas clases necesitan considerar áreas más amplias de entrenamiento para representar mejor sus características.
Conclusiones
El propósito de esta investigación fue evaluar el desempeño de los algoritmos de aprendizaje automático supervisado Support Vector Machine (SVM) y Random Forest (RF), utilizando un modelo de segmentación OBIA y variaciones en el volumen de las muestras empleadas para el entrenamiento. Para evaluar la precisión de los clasificadores, se emplearon las métricas de precisión general (OA) y el coeficiente Kappa en una imagen multiespectral de Landsat-9 OLI-2 en la zona metropolitana de Barranquilla, Colombia. Los resultados demostraron que SVM logró mayor precisión general en datos desequilibrados. Se confirmó la importancia de que las muestras de entrenamiento sean proporcionales a la superficie ocupada por las diversas cubiertas sobre el paisaje. Los resultados indicaron que para lograr precisiones de usuario superiores al 90 % en las clases de pastos limpios, bosques, red vial y agua continental mediante el modelo SVM en ArcGIS Pro, se aconseja asignar muestras de entrenamiento que abarquen el 2 %, 1 %, 3 % y 8 % del área clasificada, respectivamente. Encontrar equilibrio entre la representación precisa del paisaje y la suficiente cantidad de datos para cada clase es fundamental para construir modelos de clasificación precisos y generalizables.