INTRODUCCIÓN
A nivel mundial, la concentración de CO en la atmósfera incrementó de 280 a 407 ppm entre la era preindustrial y 2018 (NOAA c2020a), registrándose el aumento más considerable desde el inicio de la década de los 80 (NOAA c2020b). La acumulación de este gas se acrecienta a una tasa anual de 1,9 ppm (Olivo y Soto 2010), por lo que se estima que para el 2100 la concentración de CO2 atmosférico estará en 936 ppm (IPCC 2013).
El CO2 es el gas de efecto invernadero (GEI) que más contribuye al incremento de la temperatura global, por lo que incide directamente en el cambio climático (Kerr 2009). En el Ecuador las emisiones del gas rondan los 85 289,64 Gg, mientras que las absorciones solo llegan a 19 769,68 Gg (MAE 2017). Los bosques son uno de los principales sumideros de carbono al almacenarlo en su biomasa por medio de la fotosíntesis (Le Quéré et al. 2012), siendo uno de sus principales servicios ecosistémicos (Zhou et al. 2014). En 2012, los bosques del Ecuador absorbieron 18 814,40 Gg de CO2-eq, lo que representa el 98,48 % del total de absorciones del país (MAE 2017).
En varias regiones del mundo, el área cubierta por bosques secundarios es cada vez mayor (FAO 2016). Estos ecosistemas se forman luego del abandono de cultivos y pastos o por la alteración natural de la vegetación original (Finegan 1992). En Latinoamérica, hasta 2008 se registraron 2,4 millones de km2 cubiertos por bosques secundarios tropicales (Chazdon et al. 2016). En el Ecuador, de 1990 a 2014 se regeneraron 1674 km2 de ecosistemas forestales (Sierra 2013, MAE 2016), lo que implica formación de bosques secundarios.
El proceso de sucesión conlleva un cambio de diversidad y estructura florística, lo que provoca que los árboles presenten estrategias adaptativas y de competencia ecológica (Lebrija-Trejos et al. 2008, Lohbeck et al. 2013). Por lo mencionado, la acumulación de carbono en la biomasa de los bosques secundarios difiere de lo observado en bosques primarios (Lohbeck et al. 2013), siendo necesario el estudio de los cambios estructurales y funcionales de estos ecosistemas (Lavorel et al. 2011).
Existe un gran potencial de almacenamiento de carbono en los bosques secundarios por su alta producción primaria y el rápido crecimiento de las especies que los conforman (Chazdon et al. 2016). Estudios realizados en los trópicos latinoamericanos muestran gran variabilidad en la capacidad de almacenaje de estas formaciones; para el año 2017 en la Amazonía brasileña se registró en promedio 25,51 Mg.C.ha-1 (Smith et al. 2020), mientras que en los Andes colombianos, el carbono almacenado pasó de 23,8 a 111,6 Mg.C.ha-1 entre una etapa de sucesión temprana y una tardía (Clerici et al. 2016). Hay que tener en cuenta que las funciones ecológicas de estos ecosistemas, como el almacenamiento de carbono, están vinculadas a parámetros estructurales y de diversidad (Günter et al. 2007). Estos parámetros se recuperan cronológicamente en bosques secundarios y están influenciados significativamente por el clima, las fuentes semilleras, la fauna dispersora, la topografía, la edad de la sucesión y el tiempo y tipo de perturbación de la vegetación original (Hughes et al. 1999, Günter et al. 2007, Yepes et al. 2010); de ahí la gran variabilidad en cuanto a la captura y almacenaje de carbono.
Existen varios métodos establecidos por el Intergovernmental Panel on Climate Change (IPCC) para evaluar los contenidos de carbono en los bosques, entre los que se incluyen los modelos alométricos (Yamashita et al. 2012). Si bien existen modelos para bosques secundarios, estos se centran en bosques de tierras bajas (Chave et al. 2014, Puc-Kauil et al. 2019, Huang et al. 2020) y tienden a ser específicos para las condiciones en las que se desarrollaron (Saatchi et al. 2007). En este sentido, el presente estudio tuvo como objetivo generar modelos alométricos para la estimación de la biomasa aérea en bosques secundarios montanos del noroccidente de Ecuador, que permitan conocer la cantidad de carbono almacenado.
MATERIALES Y MÉTODOS
Zona de estudio
El estudio se realizó en tres bosques secundarios contiguos de 18, 30 y 50 años aproximadamente (información del propietario), ubicados al noroccidente del Ecuador entre las coordenadas 0° 20' - 0° 20' Norte y 78° 33' - 78° 33' Oeste, a una altitud de 1850 m. Políticamente se encuentran en la provincia de Imbabura, cantón Cotacachi, parroquia Pañaherrera (Fig. 1). El uso previo a la sucesión vegetal en los tres casos fue la actividad agropecuaria, en una superficie de 4,95; 8,47 y 8,87 ha, respectivamente.

Figura 1 Ubicación de los bosques estudiados WGS 1984 zona 17s. Azul= sucesión de 50 años; rojo= sucesión de 30 años; amarillo= sucesión de 18 años.
La precipitación anual varía entre 1500 y 2000 mm y la temperatura de 18 a 20 °C (INAMHI c2017). Los suelos de la zona están clasificados como andisoles, desarrollados a partir de ceniza volcánica y son de color negro, con alta presencia de alófana y complejos de humus, por lo que su densidad aparente es menor a 90 g.cm-3 (SIGTIERRAS 2017). Según la clasificación oficial de ecosistemas del Ecuador, las áreas estudiadas son parte de los Bosques siempreverdes montano bajo de Cordillera Occidental de los Andes (MAE 2013).
Inventario forestal
Para la distribución de las unidades de muestreo se usó una adaptación a la metodología aplicada para la Evaluación Nacional Forestal del Ecuador (ENF) (Aguirre et al. 2010), que propone el establecimiento de conglomerados conformados por tres parcelas principales y dos subparcelas. Dada la superficie de los bosques estudiados, se ubicó un solo conglomerado por cada ecosistema.
En la parcela A se midió el diámetro a 1,30 m del suelo (DAP, cm) y la altura total (Ht, m) de los individuos con un DAP ≥0,20 m. Cada árbol fue codificado e identificado taxonómicamente. El proceso se repitió en la parcela B con los individuos con un DAP entre 0,10 y 0,20 m y en la parcela C con los individuos que no alcanzaron los 0,10 m de DAP. Posteriormente, los DAP se transformaron a área basal mediante la ecuación: AB = π/4(DAP)2 (BOLFOR et al. 2000).
Se calculó la densidad (Dr), frecuencia (Fr) y dominancia (Dr) relativas de cada bosque, con las siguientes ecuaciones: Dr = (# individuos de la especie/# total de individuos) x 100; Fr = (# parcelas en los que aparece la especie/Σfrecuencia de todas las especies) x 100; Dr = (ΣAB de los individuos de la especie/ΣAB del total individuos) x 100. La sumatoria de los parámetros representó el índice de valor de importancia (IVI) (BOLFOR et al. 2000).

Figura 2 Distribución diamétrica (m) del número de individuos (n.ha-1) de los bosques estudiados discriminados por edad
Para determinar la diversidad de los ecosistemas se usó el índice de Shannon-Wiener (H'), con la ecuación: H' = Σ (Pi log2 Pi), donde: Pi es el valor de la abundancia relativa de la i-ésima (Krebs 1999). La similitud florística entre los sitios estudiados se obtuvo con el coeficiente de Jaccard (Cj), con la ecuación: Cj = (j/a+b-j), donde: j son las presencias compartidas, a son las especies exclusivas del sitio 1 y b las especies exclusivas del sitio 2 (Magurran 1988).
Construcción de modelos alométricos
Se calculó el volumen del fuste de los árboles registrados en el inventario con la ecuación: Vf = (DAP2*π/4)*Ht*ff ; donde: Vf es el volumen del fuste (m3); y ff es un factor de forma igual a 0,7 (MAE 2015).
Se extrajeron muestras del fuste (H = 1,30 m) con un barreno de Pressler (Ø = 0,005 m) de hasta tres individuos por especie y clase diamétrica analizada (Burkhart y Tomé 2012). Estas muestras fueron empacadas y enviadas al laboratorio para su medición, pesaje (precisión 0,0001 g) y deshidratación (105°C hasta tener un peso constante). La densidad de la madera (δ, g.cm-3) de cada individuo se determinó dividiendo el peso de la muestra deshidratada por su volumen en verde (Kenzo et al. 2017). La biomasa del fuste (Bf) de los árboles muestreados se obtuvo con: δ*Vf.
Se contabilizó el número total de ramas por individuo muestreado (#R.ind) y se extrajo una rama bifurcada directamente del fuste en el centro de la copa (valor promedio) (Ramírez y Chagna 2019); ésta fue seccionada, embalada y codificada, conjuntamente con sus hojas, para ser pesadas y deshidratadas en laboratorio. La materia orgánica de las muestras (kg) se obtuvo con la ecuación: B = (Pf * Ms)/100; donde: Pf es el peso fresco (kg) y Ms el porcentaje de material seco (Segura y Andrade 2008). Estos valores fueron multiplicados por #R.ind obteniéndose la biomasa de ramas (Br) y hojas (Bh) (Ramírez y Chagna 2019). Finalmente, la masa orgánica total de los árboles (Bt) se obtuvo con la ecuación: Bt=Bf+Br+Bh.
Para la construcción de los modelos se realizaron análisis de regresión simple y múltiple con el DAP y Ht como variables regresoras. Se comprobó que los datos cumplieran con los supuestos de normalidad, independencia y homogeneidad de varianzas; en aquellos casos que no se cumplieron se recurrió a transformaciones (Segura y Andrade 2008, Picard et al. 2012). La elección de las ecuaciones de mejor ajuste se realizó en función de: a) la variabilidad del modelo explicada por el coeficiente de determinación ajustado (R2 aj) (Bueno-López et al. 2019), b) de la precisión de las estimaciones en función a la raíz del cuadrado medio del error (RCME) (Aquino-Ramírez et al. 2015); y, c) del comportamiento de la ecuación establecido por el error absoluto medio (EAM) (Forrester et al. 2017). Se realizó una prueba de carencia de ajuste para verificar la idoneidad de los modelos desarrollados (Miller y Neill 2008).
La validación de los modelos se realizó con: a) el método de dispersión entre los observados vs predichos (Puckauil et al. 2019), b) el error medio relativo: EMR=[Σ (S-O)/ΣO)] (Djomo et al. 2010, Chave et al. 2014, Puckauil et al. 2019), c) el error absoluto promedio porcentual: EAPP=l00/n* Σ[(S-O)/O] (Cortés-Sánchez et al. 2019); y d) el coeficiente de Nash Sutcliffe EF=1-[ Σ (S-O)2*( Σ (O-Ō)2)-1] (Smethurst et al. 2020); donde: S, la biomasa simulada; O, la biomasa observada; Ō, el promedio de la biomasa observada; y n, el total de datos.
Finalmente se realizó una comparación entre el modelo general de este estudio y otros modelos realizados para bosques secundarios montanos de Colombia (Sierra et al. 2007) y bosques montanos del sur del Ecuador (Lozano-Sivisaca et al. 2018) y el norte de Colombia (Alvarez et al. 2012).
La biomasa obtenida se transformó a carbono utilizando el factor de conversión de 0,5 establecido por el IPCC (Penman et al. 2003).
RESULTADOS Y DISCUSIÓN
Caracterización de la masa forestal
Los bosques de 18 y 30 años presentaron similitud en el número y dominancia de las especies, mientras el de 50 presentó mayor riqueza florística (Tabla 1). Según la escala de H' propuesta por Magurran (1988) la diversidad es alta en el ecosistema de mayor edad y media en los restantes (Tabla 2). Lo descrito es común en sucesiones secundarias, donde el tiempo de abandono influye significativamente en la recuperación de la composición florística (Finegan 1992, Chazdon et al. 2016, Zanini et al. 2014). La sucesión más joven presenta baja similitud (Cj, Tabla 2) con las otras formaciones estudiadas, mientras que, con 17 especies en común, la semejanza entre los bosques de 30 y 50 años es del 39,53 %. Valores bajos de Cj indican que existe una alta tasa de recambio de especies entre los sitios estudiados (Márquez-Salazar et al. 2019).
Tabla 1 Resumen de información florística de los bosques estudiados.

n. fam= número de familias; n. spp.= número de especies; IVI= índice de valor de importancia.
El número de individuos (n.ha-1) en los bosques de 18, 30 y 50 años fue de 7875, 4294 y 4276 respectivamente (Fig. 2). Estos valores fueron menores a los descritos en bosques secundarios montanos de Colombia, en donde se registraron más de 10 000 n.ha-1 en etapas de sucesión temprana (hasta once años) y cerca de 5000 n.ha-1en sucesiones de 20 a 25 años (Yepes et al. 2010).
En los tres bosques estudiados la mayor cantidad de individuos se concentró en la clase diamétrica < 0,10 m, lo que es consistente con lo observado en bosques montanos del sur del Ecuador, donde el n.ha-1 en el mismo rango diamétrico fue de entre 6560 y 8280 (Günter et al. 2007).
El bosque de 18 años presentó más del doble de individuos < 0,10 m de DAP; consistente con el comportamiento de las etapas de sucesión temprana, caracterizadas por un alto número de individuos de diámetros pequeños (Saldarriaga 1991, DeWalt et al. 2003, Yepes et al. 2010). Lo mencionado es corroborado por el estudio de Yepes et al. (2010), quienes describen una disminución de individuos < 0,10 m de DAP con el incremento de la edad de la sucesión. En bosques secundarios de tierras bajas se observó la misma tendencia, contabilizándose el mayor número de individuos de diámetro bajo hasta los quince años (Kennard 2002, Ruiz et al. 2005, Higuchi et al. 2008).
El área basal y el volumen de los bosques estudiados (Tabla 3) se encuentran dentro de lo reportado para bosques secundarios tropicales (Kennard 2002, Ruiz et al. 2005, Powers et al. 2009, Lebrija-Trejos et al. 2010, Yepes et al. 2010, Avella-M et al. 2019). El área basal es similar a lo observado en bosques secundarios montanos de Colombia, donde fluctuó entre 5 y 29,7 m2.ha-1 en sucesiones de hasta once años y de 25,2 a 35,5 m2.ha-1 entre los 25 y 40 años (Yepes et al. 2010).
Tabla 3 Resumen del inventario forestal de los bosques estudiados.

n. spp.= número de especies; DAP = diámetro a la altura del pecho; CV = coeficiente de variación; Ht = Altura total; AB= área basal; Vol= volumen.
El área basal y el número de individuos de los bosques de 30 y 50 años es similar; sin embargo, el volumen es superior en el de mayor edad. Esta diferencia obedece a un incremento en altura promedio, producto del propio desarrollo de los árboles y la competencia por luz de los individuos (Finegan 1992). En ecosistemas secundarios de tierras bajas se observó crecimientos en altura hasta los 65 años, momento en el que la Ht promedio no varió considerablemente (Oliva et al. 2018).
Modelos alométricos
El DAP fue la variable de mayor significancia en los modelos desarrollados (Tabla 4), similar a lo descrito por Forrester et al. (2017). Los modelos desarrollados con el DAP2 como única variable regresora presentaron buen ajuste, lo que es recurrente en estudios de bosques tropicales (Sierra et al. 2007, Basuki et al. 2009, Alvarez et al. 2012, Douterlungne et al. 2013, Chave et al. 2014); sin embargo, la inclusión de la Ht como parte de la variable combinatoria DAP2Ht mejoró el ajuste de los modelos. Pese a su difícil medicición en campo (Segura y Kanninen 2005, Djomo et al. 2010, Ribeiro et al. 2011, Hunter et al. 2013), la inserción de la Ht reduce el error de predicción de biomasa aérea (Feldpausch et al. 2012, Chave et al. 2014, Manuri et al. 2016, Mugasha et al. 2016, Puc-kauil et al. 2019).
Tabla 4 Modelos alométricos par a la estimación de biomasa aérea.

Dap= diámetro a la altura del pecho ( m); Ht = altura total ( m); Bf = biomasa fuste (kg), Br = biomasa ramas (kg), Bh = biomasa hojas (kg), Bt = biomasa total (kg). C. C.= Coeficiente de correlación; R2aj= coeficiente de de terminación ajustado; RCME= raíz del cuadrado medio del error; EAM= error absoluto medio P= significancia de prueba de carencia de ajuste (> 0,05); EMR= error medio relativo; EAPP= error absoluto promedio por centual; EF= coeficiente Nash Sutcliffe; *= Muestra ecuación de mejor ajuste.
Tabla 5 Modelos alométricos para estimación de biomasa aérea en bosques montanos.

Dap= diámetro a la altura del pecho, otros estudios (cm), este estudio (m); Ht= altura total (m). 8= densidad de la madera (g/cm3).
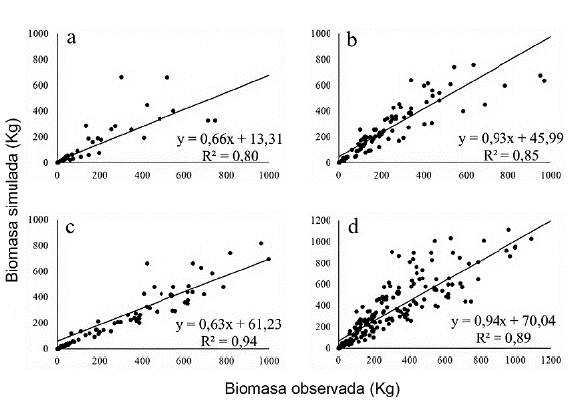
Según el coeficiente de Nash Sutcliffe (Moriasi et al. 2007), los modelos seleccionados mostraron un ajuste muy bueno, con una distorsión en la estimación (EMR) de entre -12 y 3 %. La relación lineal significativa entre la biomasa observada y la simulada, con valores de R2 superiores al 75 % (Fig. 3), muestra alta efectividad de los modelos.
El modelo general (DAP2Ht) de este estudio mostró mejor ajuste que otros para ecosistemas similares (Tabla 5), lo que confirma la necesidad de desarrollar modelos con base en datos locales (Chambers et al. 2001, Baker et al. 2004, Sierra et al. 2007, Basuki et al. 2009). Adicional a un mejor desempeño, el modelo de esta investigación utiliza variables de fácil mensuración, a diferencia del modelo de Alvarez et al. (2012) que requiere la δ. En cuanto al modelo de Sierra et al. (2007), que usa solo el DAP como regresora, este subestima cerca del 22 % de la biomasa total de los bosques, lejano al 1 % del obtenido en este estudio. Finalmente, el modelo desarrollado por Lozano-Sivisaca et al. (2018) en el sur del Ecuador, no presentó ajuste para los bosques estudiados.
Contenido de biomasa y carbono
La δ en los bosques estudiados (Tabla 6) fue similar al intervalo de entre 0,55 y 0,75 g.cm-3 determinado para bosques montanos en Colombia (Alvarez et al. 2012). Este parámetro tiene gran influencia sobre el carbono almacenado por los bosques (Kenzo et al. 2017), muestra de esto es la diferencia registrada entre los bosques de 30 y 50 años, en donde un mayor número de individuos con 8 alta, contribuyó a un almacenamiento de carbono dos veces mayor en el bosque más longevo. Aunque en promedio el bosque de 50 años presentó mayor δ, no se evidenció relación de este parámetro con la edad de sucesión, similar a lo descrito por Jones et al. (2019). Lo antedicho difiere de lo observado con el carbono, que incrementó con la edad, lo que es consistente con otros estudios de bosquesmontanos (Yepes et al. 2010, de Souza et al. 2011, Powers y Marín-Spiotta 2017).
La biomasa y carbono de los bosques de 18 y 30 años fueron similares a los de sucesiones secundarias en condiciones ambientales similares (Yepes et al. 2010, Moser et al. 2011, Peña y Duque 2013); sin embargo, el bosque de 50 años presentó valores cercanos a los de bosques primarios (Yepes et al. 2010, Peña y Duque 2013). Lo mencionado obedece a dos factores: a) los parámetros de estructura y diversidad están ligados directamente a la edad (DeWalt et al. 2003, Yepes et al. 2010, Zanini et al. 2014), por lo que a mayor edad las funciones ecológicas van asemejándose a las de bosques primarios (Hughes et al. 1999, Günter et al. 2007, Yepes et al. 2010); y b) la mayor parte de árboles tuvieron una 8 promedio de 0,61 g.cm-3, propia de especies esciófitas parciales (Palacios 2004), comunes en sucesiones avanzadas y bosques primarios (Finegan 1992).
La distribución de biomasa y carbono aéreo en los componentes estructurales de los bosques (fuste, ramas hojas) (Tabla 6), fue similar a la de bosques montanos al sur del Ecuador, donde el 94 % del carbono aéreo fue almacenado en fuste y ramas, mientras el porcentaje restante se concentró en hojas (Moser et al. 2011).
El conocimiento del aporte ecosistémico de este tipo de formaciones es fundamental para su manejo en un contexto de cambio climático, más aún cuando los bosques montanos son el segundo ecosistema de mayor almacenaje de carbono en el Ecuador con 124,11 Mg.ha-1 (MAE 2014).