doi: http://dx.doi.org/10.18257/raccefyn.317

¹ Licenciatura en Matemáticas Aplicadas, Universidad del Papaloapan, Av. Ferrocarril s/n. 68400
Ciudad Universitaria. Campus Loma Bonita, Oaxaca, México
² Departamento de Matemáticas y Estadística, Universidad del Norte, Km 5 Vía Puerto Colombia, Barranquilla, Colombia. *Corresponding author: Bernardo Uribe, bjongbloed@uninorte.edu.co

Received: November 11, 2015. Accepted: June 7, 2016

Abstract

Let G be a compact and connected Lie group and PU(H) be the group of projective unitary operators on an infinite dimensional separable Hilbert space H endowed with the strong operator topology. We study the space homst(G, PU(H)) of continuous homomorphisms from G to PU(H) which are stable, namely the homomorphisms whose induced representation contains each irreducible representation an infinitely number of times. We show that the connected components of hom_st(G, PU(H)) are parametrized by the isomorphism classes of S¹-central extensions of G, and that each connected component has the group hom(G, S¹) for fundamental group and trivial higher homotopy groups. We study the conjugation map PU(H) → hom_st(G, PU(H)), F → FaF^−1, we show that it has no local cross sections and we prove that for a map B → hom_st(G, PU(H)) with B paracompact of finite paracompact dimension, local lifts to PU(H) do exist.

Key words: Unitary Representation, Projective Unitary Representation.

Resumen

Sea G un grupo de Lie compacto y conexo y PU(H) el grupo de operadores proyectivos e unitarios en un espacio de Hilbert separable e infinito dimensional H, provisto de la topología fuerte de operadores. Estudiamos el espacio hom_st(G, PU(H)) de homomorfismos continuos desde G a PU(H) que son estables, es decir homomorfismos cuyas representaciones inducidas contienen cada representación irreducible un número infinito de veces. Demostramos que las componentes conexas del espacio hom_st(G, PU(H)) están parametrizadas por las clases de isomorfía de extensiones centrales de G por el grupo S¹, y que cada componente conexa tiene por grupo fundamental al grupo hom(G, S¹) y sus grupos de homotopía superiores son triviales. Estudiamos la aplicación conjugación PU(H) → hom_st(G, PU(H)), F → FaF^−1, demostramos que no tiene secciones locales y demostramos que para cualquier aplicación continua B → hom_st(G, PU(H)) con B paracompacto de dimensión paracompacta finita, los levantamientos locales a PU(H) sí existen.

Palabras clave: Representación Unitaria, Representación Proyectiva Unitaria.

Introduction

The motivation to study the topological properties of the space hom_st(G, PU(H)) of stable homomorphisms from a compact Lie group G to the group of projective unitary operators on a Hilbert space H endowed with the topology of pointwise convergence, comes from realm of equivariant K-theory.

By a theorem of Atiyah and Jänich Jänich (1965) the K-theory groups of a topological space X may be obtained as the homotopy groups of the space

of continuous maps from X to the space Fred(H) of Fredholm operators on H. Given any projective unitary bundle over X, namely a PU(H)-principal bundle PU(H) → P → X, we may define a twisted version of the K-theory groups by taking the homotopy groups of the space of sections of the associated Fred(H) bundle

These groups are called the twisted K-theory groups and they define a parametrized cohomology theory in the sense of May and Sigurdsson (2006) whenever we consider the category of pairs (X, f) with X a topological space and f : X → BPU(H) a map which recovers the PU(H) bundle P.

In the equivariant setup, namely when we consider the category of spaces with G actions, the definition of the twisted equivariant K-theory is more intricate. We need to consider G equivariant projective unitary stable bundles, namely G equivariant PU(H)-principal bundles P → X, such that the induced local homomorphism G_x → PU(H) is stable for G_x the isotropy group of any x ∈ X, in order to define the twisted equivariant K-theory groups as the homotopy groups of the G invariant sections of the associated bundle

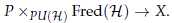
To prove that the twisted equivariant K-theory is a parametrized cohomology theory in the sense of May (1996) we would need to construct a universal G equivariant projective unitary stable bundle as it was done in the non-equivariant case. The construction of this universal space can be done using classifying spaces of families of subgroups as it was done in Lück and Uribe (2014), though the property of being locally trivial depends on the existence of cross local sections on the conjugation map

Unfortunately such local cross sections fail to exist in general, as we shown in Theorem 4.8, and therefore the universal space that we can construct using families of subgroups fails to be locally trivial. Nevertheless when we restrict ourselves to consider only maps

with B paracompact, we prove in Theorem 5.6 that these maps have indeed local lifts to PU(H). The previous result would imply that the universal space constructed using classifying spaces of families of subgroups done in Lück and Uribe (2014) would become a universal G equivariant projective unitary stable bundle for paracompact spaces, and hence, when restricted to paracompact spaces, the twisted equivariant K-theory would be a parametrized equivariant cohomology theory. We have not proven this last statement, but we believe it is true.

Besides the application of our results to K-theory, we also show the following facts. We study the space of stable unitary representations hom_st(G,U(H)) on a Hilbert space H and we generalize results of Dixmier-Douady on the infinite grassmannian G_r(H) to the space of unitary representations. We show in Corollary 4.10 that hom_st(G,U(H))C is weakly homotopy equivalent to a point for any choice of irreducible representations C ⊂ Irrep(G), we show that the space hom_st(G, PU(H)) has as many connected components as S¹-central extensions of G and that each connected component has hom(G, S¹) for fundamental group and trivial higher homotopy groups.

The article is organized as follows. In Section 2 we recall the properties of the group of unitary operators endowed with the strong operator topology and we define the infinite grassmannian. In Section 3 we recall the definition of continuous field of Hilbert spaces done by Dixmier-Douady in Dixmier and Douady (1963) and we show the properties of the infinite grassmannian with respect to the existence of sections on the unitary group. In Section 4 we study the topological properties of the spaces

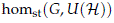
of stable continuous homomorphisms from a compact Lie group to the group of unitary operators. In Section 5 we study the topological properties of the space

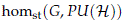
of stable continuous homomorphisms from a compact Lie group to the group of projective unitary operators. Finally, in Section 6 we show some applications to twisted equivariant K-theory of the results of the previous sections and we conclude with some ideas for further research.

Acknowledgements: The first author acknowledges the support of a CONACyT postdoctoral fellowship and of the Centro de Ciencias Matemáticas of the UNAM. The second author acknowledges the financial support of the Max Planck Institute for Mathematics in Bonn and of COLCIENCIAS through contract number FP44842-617-2014.

Spaces of operators and the infinite grassmannian

Let H be a separable and infinite dimensional complex Hilbert space and denote by B(H) the vector space of bounded linear operators. The inner product á,ñ on H induces the norm çxç := 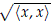for x ∈ H, and we have the standard norm on the space of bounded linear operators

The space B(H) can be endowed with several topologies, among them we have the strong operator topology and the compact-open topology. These topologies are of interest when studying principal bundles and therefore are the ones of interest in this paper.

Recall that in the strong operator topology, a subbasic open set is given by

for any T ∈ B(H), x ∈ H and e > 0. In this topology, a sequence of bounded operators {T_n} converges to T ∈ B(H) if and only if T_nx → T_x for all x ∈ H. On the other hand, a subbase for the compact-open topology on B(H) is given by the family of sets

where K ⊂ H is a compact set and A ⊂ H is an open set. Note that in the compact-open topology a sequence of bounded operators {T_n} converges to T ∈ B(H) if and only if T_nç_K → Tç_K uniformly for every compact set K ⊂ H.

Neither of the previous topologies on B(H) are equivalent. However, if we restrict to the group of unitary operators on H,

then we know that the strong operator topology and the compact-open topology agree on the group U(H). Moreover, the group U(H) endowed with any of these topologies is a Polish group, i.e. a completely metrizable topological group (see Espinoza and Uribe (2014)), and furthermore contractible (Dixmier and Douady, 1963, §11, Lem. 3). Let us recall the metric on U(H) which recovers the strong operator topology since it will be needed in what follows.

Let {e_j}_j∈N be an orthonormal base of H and consider the embedding Y : U(H) → H^N with Y(T) = (Te_j)_j∈N. Any metric on H^N which induces the product topology induces also a metric on U(H) compatible with the strong operator topology. Therefore for any pairs of operators T,U ∈ U(H) we may define their distance by the equation

Note that with this metric S¹ acts by isometries on U(H), i.e.

and moreover we have that

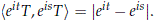
From now and on we will assume that U(H) is endowed with the strong operator topology and with the metric defined above. The first consequence of this choice is the following lemma.

Lemma 2.1. Let X be a topological space and let us consider U(H) with the strong operator topology. Then a map Y : X → U(H) is continuous if and only if the map

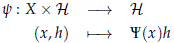
is continuous.

Proof. Consider (x₀, h₀) ∈ X×H and let

be an open ball in H with center at y(x₀, h₀) = Y(x₀)h₀ and radius e > 0. We will show that there exists an open set A ⊂ X×H such that y(A) ⊂ B(Y(x₀)h₀, e).

Define V(Y(x₀), e/2; h₀) = {T∈ U(H) ç Th₀ ∈ B(Y(x₀)h₀, e/2)} which is an open set in the strong operator topology on U(H). Then U = Y^−1(V(Y(x₀), e/2; h₀)) is an open set in X.

Let us see that the open set

has the desired properties. Indeed, for (x, h) ∈ A we have

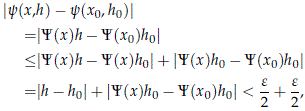
and therefore A ⊂ y ^−1 (B(Y(x₀)h₀, e)).

By (Munkres, 2000, Thm. 46.11) the reciprocal statement is true whenever U(H) is endowed with the compactopen topology. Since the strong operator topology and the compact-open topology agree on U(H) the lemma follows.

Recall that an orthogonal projector P on the Hilbert space consist of an operator P : H → H such that P² = P with the property that ker(P) and Im (P) are orthogonal. Define the infinite grassmannian as follows

and endow it with the strong operator topology.

Since the map

is an embedding, and U(H) is a Polish group, then Gr(H) is metrizable. Moreover, since Gr(H) is closed in U(H) we have that the infinite grassmannian Gr(H) is a completely metrizable space.

Continuous fields of Hilbert spaces

The following is the definition of Dixmier and Douady Dixmier and Douady (1963) applied to the case of Hilbert spaces.

Consider B a topological space and denote by O(B) the algebra of continuous complex valued functions on B. Let (E(z))_z∈B be a family of Hilbert spaces. For Y ⊂ B, an element in P _z∈Y E(z), i.e. an assignment s defined on Y such that s(z) ∈ E(z) for all z ∈ Y, will be called a vector field over Y. For s a vector field over Y, we will denote by ççsçç the map z → ççs(z)çç taking values in R.

Definition 3.1. (Dixmier and Douady, 1963, Def. 1, pp 228) A continuous field of Hilbert spaces E over the topological space B is a family (E(z))_z∈B of Hilbert spaces, endowed with a set G ⊂ P_z∈BE(z) of vector fields, such that:

• G is a sub-O(B)-module of P_z∈B E(z).
• For all z ∈ B and all x∈ E(z), there exists s∈ G such that s(z) = x.
• For all s ∈ G, the map ççsçç is continuous.
• If s ∈ P_{z ∈ B} E(z) is a vector field such that for all z ∈ B and every e > 0 there exists s' ∈ G satisfying ççs − s'çç ≤ e on a neighborhood of z, then s ∈ G.

The elements of G will be called continuous vector fields of E.

Let H be a Hilbert space and G the space of continuous maps from B to H. For every z ∈ B define E(z) := H. Then E = ((E(z))z∈B,G) is a continuous field of Hilbert spaces and will be called the constant field over B defined by H.

Following (Dixmier and Douady, 1963, §12), denote by D₀ the constant field over Gr(H) defined by H and denote by D the canonical field over Gr(H) defined by the family of vector spaces (P(H))_P∈Gr(H), where G is the set of vector fields parametrized by the elements in H

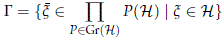
with `x(P) := P(x). Denote by D^{^} the family of vector spaces (P(H)^{^})_P∈Gr(H) and note that both D and D^{^} are sub-fields of D₀ and moreover D ⊕ D^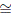{^} D₀.

From Theorem 2 in (Dixmier and Douady, 1963, §12), it follows that the canonical field over the infinite grassmannian is trivial if Gr(H) has the norm topology. Nevertheless whenever Gr(H) is endowed with the strong operator topology, then the canonical field is not locally trivial (Dixmier and Douady, 1963, §16, Cor. 2).

The continuous field D over Gr(H) is a universal continuous field for continuous fields of infinite dimensional Hilbert spaces over paracompact spaces. This fact follows from (Dixmier and Douady, 1963, §14, Cor. 1) which we quote here: Let E be a continuous field of infinite dimensional and separable Hilbert spaces over the paracompact space B. Then there exist a continuous map f : B → Gr(H) such that E f*D.

Dixmier and Douady show this fact in (Dixmier and Douady, 1963, §13, Thm. 3) by constructing vector fields {_n}_n∈N ⊂ G which are orthogonal over f(B) and such that for all P ∈ f(B) the set {_n(P)}_n∈N is an orthonormal base for P(H). With these sections at hand Dixmier and Douady furthermore show in (Dixmier and Douady, 1963, §15, Thm. 5) that E is trivializable.

Lemma 3.2. Let B be a paracompact space of finite paracompact dimension and f : B → Gr(H) a continuous map. Take b0 B and define the conjugation map

Then there exist a continuous map s : B → U(H) such that the following diagram is commutative

Proof. Since f*D ⊕f*D^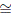{^} B × H and f*D is trivializable, in (Dixmier and Douady, 1963, §14, Thm. 4) it is shown that there exist sections {_n}_n∈N, {_n}_n∈N for f*D and f*D^{^} respectively which are pointwise orthonormal, i.e. {_n(b)}_n∈N is an orthonormal base for f(b)(H) and {_n(b)}_n∈N is an orthonormal base for (Id - f(b))(H).

Define the map y : B×H→H by the assignment

and note that y is continuous. By Lemma 2.1 the map s : B → U(H) defined by the equation y(b, h) = s(b)h is continuous and we have that

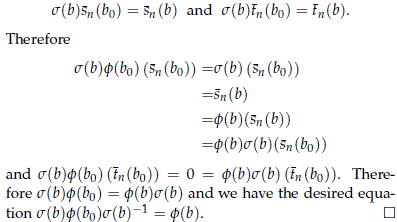
We have just shown that over paracompact spaces we may construct sections of the conjugation map. But these sections fail to exist whenever the base is the infinite grassmannian.

Lemma 3.3. Let Q ∈ Gr(H) be a projector. Then, the map

has no global sections.

Proof. Let us proceed by contradiction. Suppose that there exists a continuous map s : Gr(H) → U(H) such that s(P)Qs(P)^−1 = P. By Lemma 2.1 we know that the evaluation map (P, h) → s(P)h is continuous. Hence the map (P, h) → (P, s(P)h) is also continuous, and its restriction

is continuous. This map trivializes the canonical field D over Gr(H) but this contradicts (Dixmier and Douady, 1963, §16, Cor. 2) where it is shown that D is nowhere locally trivial.

Π

The map p_Q is surjective in Gr(H) since any two orthogonal projectors in Gr(H) are conjugate. Therefore the map

p_Q induces a continuous map

where U(H)_Q = {T ∈ U(H) ç TQT^−1 = Q} is the isotropy group of Q, which is moreover bijective but which is not a homeomorphism. This last statement follows from (Dixmier and Douady, 1963, §16, Cor. 2) where it is shown that D is nowhere locally trivial thus implying that the map PQ is not a U(H)_Q-principal bundle over Gr(H).

Nevertheless, the existence of extensions that were shown in Lemma 3.2 implies that the pullback f*U(H) over B of a fixed map f : B → Gr(H) is indeed a U(H)_f(b0)- principal bundle. If f*U(H) = {(b, F) ∈ B × U(H) ç f(b) = p_f(b0)(F)} then the map

is a U(H)_f(b0)-bundle isomorphism.

We conclude this section by stating that Gr(H) is a classifying space for Hilbert space bundles over paracompact spaces. This follows from the following three facts: First, any continuous field of infinite dimensional Hilbert spaces over a paracompact space B is isomorphic to the pullback over some map of the canonical field D over Gr(H). Second, any continuous field of infinite dimensional Hilbert spaces over a paracompact space is trivial. Third, the infinite grassmannian Gr(H) is contractible. Hence any two maps from B to Gr(H) are homotopic, and any two continuous fields of infinite dimensional spaces over B are isomorphic.

Spaces of unitary representations

Let G be a compact Lie group and consider a continuous homomorphism a : G → U(H). The homomorphism a induces the structure of a G representation to H denoted by H_a and we have a canonical decomposition of H_a in isotypical components

where Irrep(G) denotes the isomorphism classes of irreducible representations of G, V is a representative of its isomorphism class of irreducible representation and H_a^V is the isotypical subspace associated to V. By Schur's Lemma, the isotypical part associated to V may be defined as the image of the evaluation map, i.e.

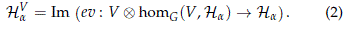
with ev(v ⊕ f) = f (v).

Definition 4.1. Let a : G → U(H) be a continuous homomorphism from a compact Lie group G to U(H). We say that the homomorphism is stable if all the isotypical components of H_a are either infinite dimensional or zero dimensional. We will denote the set of stable homomorphisms as hom_st(G,U(H)).

The set of all homomorphisms hom(G,U(H)) can be endowed with the subspace topology of the compact-open topology of the space

of continuous maps from G to U(H), and a subbase for this topology is given by the family of sets

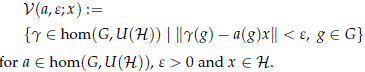
On the other hand, since G is compact and U(H) is metrizable, we may also endow

with the supremum metric, i.e. for

we define

By (Munkres, 2000, Thm. 46.8) we know that these two topologies agree. Moreover, since U(H) is complete we know that map(G,U(H)) is also complete (Munkres, 2000, Thm. 43.5).

Lemma 4.2. The space hom(G,U(H)) is a complete metric space.

Proof. Since map(G,U(H)) is complete we may take a convergent sequence {a_n}_n∈N of homomorphisms which converge to a ∈ map(G,U(H)). We know that

Therefore a is also a homomorphism and hence
hom(G,U(H)) is complete.

Π

Lemma 4.3. The space of stable homomorphisms hom_st(G,U(H)) is not closed in hom(G,U(H)).

Proof. We will show a convergent sequence in hom_st(S¹,U(H)) whose limit is not stable. The argument for any compact Lie group is similar.

Let {e_j}_j∈N be an orthonormal base of H. Define the homomorphisms a_k : S¹ → U(H) by the assignment

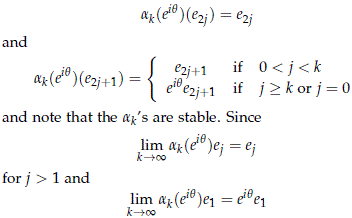
we know that lim_k→∞a_k does not belong to the space of stable homomorphisms.

Π

Lemma 4.4. The space hom_st(G,U(H)) of stable homomorphisms is not open in hom(G,U(H)).

Proof. We will prove that for any basic open set V ⊂ hom(G,U(H)) and a ∈ V a stable homomorphism, there exist a non stable homomorphism b ∈ V.

and let H = V₁ ⊕···⊕ V_n be the direct sum of the irreducible representations V_k of G, such that x_k ∈ V_k for each k = 1, . . . , n. It follows that H is a-invariant and finite dimensional.

Let b : G → U(H) be given by

Then b ∈ V by construction, but a and b are not unitary equivalent, i.e. b is not stable.

Π

Lemma 4.5. The space hom_st(G,U(H)) of stable homomorphisms is dense in hom(G,U(H)).

Proof. Let a ∈ hom(G,U(H)) be a homomorphism and let V(a,e ; x₁, . . . , x_n) be a basic open set based at a ∈ V. Consider the finite dimensional and a-invariant space H = V₁ ⊕···V_n given by the direct sum of the irreducible representations V_k of G, such that x_k ∈ V_k for each k = 1, . . . , n. If y is an isometric isomorphism y : L²(G) ⊗ L²([0, 1]) → H⊖H, then

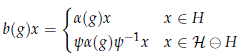
is a stable homomorphism and b ∈ V.

Π

Definition 4.6. Let C ⊂ sIrrep(G) be a choice of irreducible representations of the group G. Define

to be the space of homomorphisms which induce representations where only the irreducible representations in C appear. Define

The spaces hom_st(G,U(H))_C are neither closed nor open, nevertheless the action by conjugation of U(H) on hom_st(G,U(H))_C is transitive and we are interested in studying the properties of this action.

Definition 4.7. Take a stable homomorphism a ∈ hom_st(G,U(H))_C. Define the conjugation map

The map p_a is continuous and is surjective. Any other stable homomorphism

induces an isomorphism H 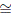⊕_V∈C H_a'^V. For each V ∈ C choose a G-equivariant unitary isomorphism F^V : H_a^V → 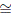H_a'^V and assemble them into a G-equivariant unitary automorphism

is a continuous map which is moreover bijective, where U(H)_a := {T ∈ U(H) çTaT^-1 = a} is the isotropy group of a. We will show that this map is not a homeomorphism, thus implying that the p_a is not a U(H)_a-principal bundle. Nevertheless, the pullback of p_a for maps defined on paracompact spaces is indeed a U(H)_a-principal bundle.

Theorem 4.8. Suppose that C contains the trivial representation, then the conjugation map p_a: U(H) → hom_st(G,U(H))_C has no sections.

Proof. Note that in the case that G = Z/2Z we have a homeomorphism

The same proof of Lemma 3.3 shows that the map p_a : U(H) → hom_st(Z/2Z,U(H)) has no sections.

The proof of the general case is based on the non existence of sections for the canonical field over the infinite grassmannian. We just need to find an appropriate injective map from Gr(H) to hom_st(G,U(H))_C

Choose a representation V ∈ C different from the trivial representation. Take the isotypical decomposition of H 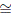⊕_W∈C H_a^W defined by a. Consider the infinite grassmannian

of the Hilbert space hom_G(V,H_{aV) and for each Z ∈ Gr(homG(V,Ha^V) denote by ev(V ⊗ Z) the subspace of Ha^V defined by the image of V ⊗ Z) under the evaluation map}

with ev(v ⊗ f) = f (v) that was previously defined in (2).

Denote by ev(V ⊗ Z)^{^H_aV} the orthogonal complement of ev(V ⊗ Z) in H_a^V, i.e

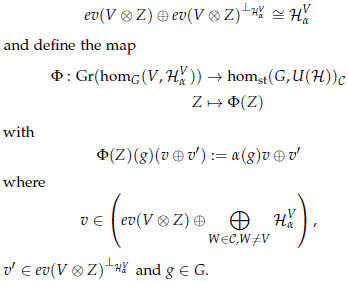
Note that the homomorphism F(Z) only disagrees with a on the subspace ev(V ⊗ Z)^{^h_aV}, that the isotypical subspace of the homomorphism F(Z) associated to V is precisely ev(V ⊗ Z), i.e.

The map F is continuous since it can be defined as the composition of projections, and it is moreover injective.

which implies that s(F(Z)) induces a G-equivariant unitary isomorphism between the isotypical components

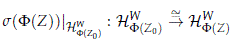
and in particular it induces a G-equivariant isomorphism

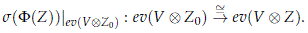
Denote by D the canonical continuous field of Hilbert spaces over Gr(hom_G(V,H_a^V) defined as follows:

and construct the following map:

Note that the homomorphism s(F(Z)) o f₀ belongs to Z, since the image of f lies in H_F^V_(Z0) and the unitary isomorphism

is G-equivariant; hence

Moreover the map q is continuous since s is continuous, and its inverse map is simply s^−1(Z, f) = (Z, s(F(Z))^−1 f). Therefore q would be a trivialization of the canonical field D which contradicts (Dixmier and Douady, 1963, §16, Cor. 2) where it is shown that D is nowhere locally trivial.

Then the section s cannot exist and the theorem follows.

Theorem 4.9. Let K be an abelian compact Lie group, B a paracompact space of finite paracompact dimension, with base point b₀ ∈ B and f : B → hom_st(K,U(H))_C a continuous map with C ⊂ Irrep(K). Then there exist an extension s : B → U(H) that makes the following diagram commutative

Proof. Since all irreducible representations of K are 1-dimensional, let us encode the information of each irreducible V ∈ Irrep(K) by a homomorphism c_V : K → S¹ ⊂ C. Choose a normalized left and right invariant measure on K, and for any a ∈ hom_st(K,U(H))_C define the operator

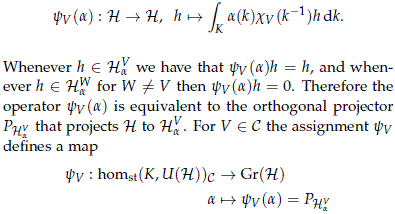
which is continuous since the integration is over a compact Lie group.

Define the map f : B × H → H by the assignment

for all V ∈ C. In particular we have that

and note that the argument above implies that s makes the following diagram commutative

is injective since for abelian groups the isotypical spaces determine the homomorphism. Therefore the following diagram is commutative

Corollary 4.10. Let G be a compact and connected Lie group, B a paracompact space with finite paracompact dimension, with base point b₀ ∈ B and f : B → hom_st(G,U(H))_C a continuous map with C ⊂ Irrep(G). Then there exist an extension s : B → U(H) that makes the following diagram commutative

Proof. Let K be a maximal abelian subgroup of G and denote by i : K → G the inclusion. Recall that any representation of the group G is uniquely determined by its restriction to a maximal abelian subgroup, and therefore the restriction map

is injective. Here we have denoted by i*C ⊂ Irrep(K) the set of irreducible representations in K which appear as restrictions of representations V of C.

By Theorem 4.9 we know that there exists s for the composition map

The previous results have the following consequence:

Theorem 4.11. Let G be a compact Lie group which moreover is connected or abelian, and C ⊂ Irrep(G) a choice of irreducible representations. Then the space hom_st(G,U(H))_C is weakly homotopy equivalent to a point.

Proof. We know that hom_st(G,U(H))_C is connected since the conjugation map

is surjective for any choice of a ∈ hom_st(G,U(H))_C.

Take any base point map

Spaces of projective unitary representations

Let H be a separable and infinite dimensional Hilbert space. Let U(H) denote the group of unitary operators of H and let PU(H) be the group of projective unitary operators, defined as the quotient of U(H) by its center,

where the center Z(U(H)) is identified with S¹. Then PU(H) fits in the following short exact sequence of groups

The group of projective unitary operators may be endowed with the strong operator topology, and in (Simms, 1970, Thm. 1) it is shown that this topology agrees with the quotient topology. Since S1 acts on U(H) by isometries, we may endow the group PU(H) with the metric defined by the distance between the orbits, i.e. for T,U ∈ PU(H) define

be a continuous homomorphism. The homomorphism a defines a projective and unitary representation of G on the projective Hilbert space PH := H−{0}/C*.

Since the kernel of the homomorphism

and make the following definition:

Definition 5.1. A continuous homomorphism a : G → PU(H) will be called stable whenever the induced homomorphism : _a → U(H) belongs to hom_st(_a, U(H))_S(Ga). Denote the set of stable homomorphisms from G to PU(H) by hom_st(G, PU(H)).

Since G is compact and PU(H) is a metric space, the set of stable homomorphisms

By (Munkres, 2000, Thm. 46.8) this metric induces the compact-open topology on hom_st(G, PU(H)).

Recall that a S¹-central extension of a Lie group G is an extension of G which fits in the short exact sequence of Lie groups

such that p₁ o f = p₀. Denote by Ext(G, S¹) the set of isomorphism classes of S¹-central extensions of G and denote by [ ] the isomorphism class of an extension.

Proposition 5.2. Let G be a compact Lie group. Then the canonical map

Proof. Let us show first that every isomorphism class of a S¹-central extension arises as the pullback of a stable homomorphism from G to PU(H). Consider an extension → G, take the Hilbert space H' := L²() ⊗ L²(-{0, 1}-) where L² denotes square integrable functions and take the standard action of G on L²(). By Peter-Weyl's Theorem the Hilbert space H' contains each irreducible representations of infinitely number of times. Take the isotypical part corresponding to the irreducible representations in S()

thus inducing a homomorphism G → PU(H). Therefore all S¹-central extensions of G appear as pullbacks of stable homomorphisms from G to PU(H).

Take representatives for each isomorphism class of S¹-central extension and denote by

Now consider the abelian group hom(G, S¹) of continuous homomorphisms from G to S¹ endowed with the group structure given by pointwise multiplication. For every

Therefore we have an action of hom(G, S¹) on hom_st(, PU(H))_S() as follows:

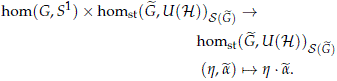
We claim the following theorem.

Theorem 5.3. Let G be a compact Lie group which is connected or abelian, and let be a S¹-central extension of G. Let S() be the set of isomorphism classes of irreducible representations of on which ker ( → G) acts by multiplication of scalars. Then the map

This assignment is indeed a homomorphism since we have the equalities

We need to show now that Y is a local homeomorphism. Note that for any non trivial h ∈ hom(G, S¹) and 1 the trivial homomorphism, we have that á1,hñ ≤ √2 since any non trivial homomorphism must take at least one value in the subset 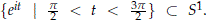. This implies that for any ∈ hom_st(, PU(H))_S() and any h ∈ hom(G, S¹) we have

is bijective and continuous, we claim furthermore that it is a homeomorphism. Let us show that Yç_Bs() ^−1 is continuous.

this s exists by the definition of the strong operator topology and the metric defined in equation (1).

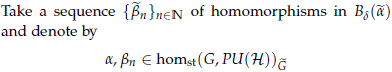
the projective homomorphisms that and n define. Assume that lim_n→∞bn = a; let us show that this implies that lim_n→∞n= .

and

Lemma 5.5 shows that çS _W≠V y^W_n ç < e. Therefore we obtain

and since çy^W_n ç > 1 - e, we have that for all k ∈ K and all n > N

is an embedding since is connected and any representation of is uniquely determined by its restriction to ˜K; hence we conclude that

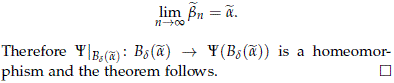
Corollary 5.4. Let G be a compact Lie group which is connected or abelian, and let be a S1-central extension of G. Then hom_st(G, PU(H))_S() is a K(hom(G, S¹), 1), namely it is connected, its fundamental group is hom(G, S¹) and its higher homotopy groups are trivial.

Proof. The result follows from Theorem 5.3 where it is proven that

Proof. Note first that c_W(c_V)^−1 = c_{W⊗ V−1} and therefore

Since ˜K is isomorphic to a product of cyclic groups, we claim that it is enough to show the lemma whenever ˜K is S¹.

Here the irreducible representations of S¹ are parametrized by n ∈ Z and our hypothesis becomes

Therefore we have that for all prime p we have that the inequalities

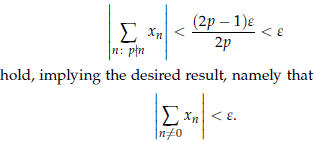
The iteration of the previous argument shows the lemma for any abelian compact Lie group.

Π

Proof. Take any lift ∈ hom_st(, U(H))_S() such that Y() = f(b₀) and consider the following commutative diagram

Applications and further research

One very important application of the existence of lifts for paracompact spaces shown in Theorem 5.6, is the construction of universal equivariant projective unitary and stable bundles necessary for the study of the twisted equivariant K-theory as an equivariant parametrized cohomology theory (see (Barcenas, Espinoza, Joachim and Uribe, 2014, Chapter 5) and (Atiyah and Segal, 2004, Chapter 6)). The construction of these universal bundles relies on the construction of classifying spaces for certain families for subgroups, together with explicit topological properties that the groups and the associated spaces of homomorphisms need to satisfy. In what follows we will review these constructions and we will show the implications that the results proved in the previous sections have on the existence of universal equivariant projective unitary bundles.

Let G and P be topological groups. A G-equivariant P-principal bundle consists of a P-principal bundle p : E → X together with left G actions on E and X commuting with the right P action on E such that p is G-equivariant. For every e ∈ E we obtain a local representation re : Gp(e) → P determined by g^−1 · e = e · r_e(g) for g ∈ G_p(e) where G_p(e) is the isotropy group of p(e) X.

In (Lück and Uribe, 2014, Thm. 11.4) it was constructed a universal G-equivariant P-principal bundle with a prescribed family of local representations through the use of classifying spaces of families of subgroups. The fact that these classifying spaces of families of subgroups permitted to obtain equivariant principal bundles relied on topological properties of the groups G and P and on the spaces of prescribed homomorphisms. Let us recall the main ingredients.

A family R of local representations for (G, P) is a set of pairs (H, a), where H is a subgroup of G and a : H → P is a continuous group homomorphism, such that the family is closed under finite intersections, under conjugation in P and under conjugation in G (see (Lück and Uribe, 2014, Def. 3.3) for a detailed description).

It is said (Lück and Uribe, 2014, Def. 6.1) that the family R satisfies Condition (H) if the following holds for every (H, a)∈ R:

• The path component of a in hom(H, P) is contained in the orbit {pa p^−1 çp ∈ P}.
• The projection P → P/P_a has a local cross section where P _a = {p ∈ P ç p ap^−1 = a } is the isotropy group of under the conjugation action of P.
• The projection G → G/H has a local cross section.
• The canonical map

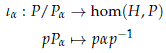
is a homeomorphism into its image.

To a family of local representations R we can associate a family of subgroups of G × P consisting of the set F(R) := {K(H, a)ç (H,a)∈ R} where K(H, a) := {(g,a (g)) ç g ∈ H}. Let

be the classifying space for the family of subgrups F(R), i.e. a (G × P)-CW-complex whose isotropy groups belong to F(R) and for which the K(H, a)-fixed point set E_F(R)(G × P)^K(H,a) is nonempty and weakly contractible for every (H, a)∈ R.

Theorem 11.4 of Lück and Uribe (2014) claims that if the family of local representations R satisfies Condition (H), then E(G, P,R) → E(G, P,R)/P is a G-equivariant P-principal bundle which is moreover universal for Gequivariant P-principal bundles whose local representations appear in R.

In this paper we are interested in G equivariant projective unitary stable bundles, namely G-equivariant PU(H)- principal bundles whose local representations (H, a) consist of stable homomorphisms a : H → PU(H) as were defined in Definition 5.1.

Whenever PU(H) is endowed with the norm topology (let us denote it by PU(H)_n), G is a topological group and S consists of the family of local representations (H, a) where H is a finite subgroup of G and a ∈ hom_st(H, PU(H)_n) is a stable homomorphism. Theorem 15.12 of Lück and Uribe (2014) shows that the bundle

is a universal G equivariant projective unitary stable bundle for almost free G-CW-complexes

It would be expected that a similar statement would hold whenever we expand the family of local representations for pairs (H, a) where H is a compact Lie group and a is a stable homomorphism. Unfortunately this is not the case for the following reasons: whenever H is a compact Lie group which is not finite, the space of stable homomorphisms to PU(H)_n in the norm topology is empty, i.e. hom_st(H, PU(H)_n) = .

If we consider the group PU(H) endowed with the strong operator topology, as it is done throughout this article, the family of local representations S consisting of pairs (H, a) with H a compact Lie group and a ∈ hom_st(H, PU(H)) does not satisfy Condition (H) of Theorem 11.4 of Lück and Uribe (2014). In particular the canonical map

is not a homeomorphism into its image, since Theorem 4.8 implies that canonical map

has no local sections.

Nevertheless, by Theorem 5.6 we know that local lifts exists if we restrict to maps

with B paracompact. Hence we might say that a Weak Condition (H) is satisfied whenever Condition (H) holds on the image of maps B → hom_st(H, PU(H)) where B is paracompact. With this setup in mind, we conjecture that the space

would become a universal space for G-equivariant projective unitary stable bundles whenever we restrict our study to the category of paracompact spaces with proper G actions. If this were the case, we would have a space that would allow us to show that the twisted equivariant K-theory is indeed an equivariant parametrized cohomology theory as defined in May (1996).

Finally note that in order for the previous statement to be true we would need to be able to generalize Theorem 5.6 for compact Lie groups which are not necessarily connected, and we would need to show that the proof of Theorem 11.4 of Lück and Uribe (2014) would work if we restrict only to the image of paracompact spaces. These tasks are beyond the scope of this article and we leave them for further research.

 

References

Atiyah, M. and Segal, G. (2004) Twisted K-theory. Ukranian Mathematical Bulletin, 1(3):291-334.         [ Links ]

Bárcenas, N., Espinoza, J., Joachim, M. and Uribe,B (2014) Universal twist in equivariant K-theory for proper and discrete actions. Proc. Lond. Math. Soc. (3), 108(5):1313-1350.         [ Links ]

Dixmier, J. and Douady, A. (1963). Champs continus d'espaces hilbertiens et de C*-algèbres. Bull. Soc. Math. France, 91:227-284.         [ Links ]

Espinoza, J. and Uribe, B. (2014). Topological properties of the unitary group. JP Journal of Geometry and Topology, 16(1):45-55.         [ Links ]

Jänich, K. (1965). Vektorraumbündel und der Raum der Fredholm-Operatoren. Math. Ann., 161:129-142.         [ Links ]

Lück, W. and Uribe, B. (2014). Equivariant principal bundles and their classifying spaces. Algebraic and Geometric Topology, 14(4):1925-1995.         [ Links ]

May, J. P. (1996). Equivariant homotopy and cohomology theory, volume 91 of CBMS Regional Conference Series in Mathematics. Published for the Conference Board of the Mathematical Sciences, Washington, DC; by the American Mathematical Society, Providence, RI.         [ Links ]

May, J. P. and Sigurdsson, J. (2006). Parametrized homotopy theory, volume 132 of Mathematical Surveys and Monographs. American Mathematical Society, Providence, RI.         [ Links ]

Munkres, J. R. (2000). Topology, Second Edition. Prentice-Hall, Inc., Englewood Cliffs, N.J.         [ Links ]

Simms, D. J. (1970) Topological aspects of the projective unitary group. Proc. Camb. Phil. Soc., 68:57-60.         [ Links ]