Introduction

Perovskite materials (SHNO) represent a great percentage of systems which are actually investigated by the physics and chemistry of solids. In general, perovskites is represented by the ideal formula ABX3, where A is an alkaline earth element, B represents a transition metal or rare earth element and X, usually is the oxygen (^{Hazen, 1988}). The modifications of atomic radii of A and B introduce structural distortions and new crystalline phases while inclusions of rare earth elements give the possibility to produce materials with exotic electric and magnetic properties (^{Kruth & West, 2001};^{Llamosa, et al., 2009}). Partial substitutions of the A and B cations give rise to complex materials such as the double perovskites with generic formula A₂BB’O₆ (^{Triana, et al. , 2012}) and other more complex perovskites (^{Moreno, et al., 2008}). Its chemical configuration offers multiple chances to combine different elements, as well as the possibility to synthesize new materials involving a great variety of physical properties. Depending on magnetic and electric characteristics of B and B’ it is relatively easy to create new perovskite systems with half-metallic properties (^{Erten, et al., 2011}), magnetoelectric response (^{Molegraaf, et al., 2009}) or magnetic ordering (^{Lee & Marianetti, 2018}), which offer promissory perspectives in the new field of spintronics technology (^{Pilo, et al., 2017}). In this paper, we propose the synthesis and characterization of the Sr ₂ HoNbO ₆ ceramic material. We describe the crystalline structure of this double perovskite and perform morphological, magnetic, and electronic analyses. Furthermore, we present the results of our measurements of the magnetic response as a function of temperature. Moreover, considering that in recent years the density functional theory (DFT) has become a good tool to study electronic properties in perovskite-like material (^{Bonilla, et al., 2008};^{Landínez-Téllez, et al., 2013}), we conducted a study of the electronic properties of these materials in order to establish the type of hybridization between the orbitals of HoO ₆ and NbO ₆ octahedra present in the structure. This calculation is the greatest motivation of this work and the experimental corroboration of the theoretical predictions with regard to the energy gap.

Experiments

Samples of SHNO were prepared by the solid-state reaction technique. Stoichiometric ratios of precursor powders SrCO₃, Ho₂O₃, and Nb₂O₅ (purity 99,90%) were finely ground and thoroughly mixed. The precursor powder was calcined at 1100 °C for 148 h in ambient atmosphere. Then, the calcined mixture was again crushed, finely ground and pressed at 6 ton/cm² pressures to form a disc (10 mm diameter, 2 mm thickness). This disc was sintered at 1300 °C for 17 h and furnace-cooled to room temperature. The structural characterization was carried out by analyzing the X-ray diffraction (XRD) data obtained from a Panalytical® X-Pert PRO MPD diffractometer (CuKα=1,540598 Å). Refinements of the experimental data were performed through the GSAS code. The XRD pattern of the sample was recorded for crystallographic phase characterization. The morphological characterization of samples was systematically effectuated from scanning electron microscopy (SEM), by using VEGA 3 equipment. The field cooling measurement of the magnetic susceptibility as a function of temperature was carried out with an MPMS® Quantum Design SQUID.

Theoretical calculations. We used the Wien2k program (^{Blaha, et al., 2001}) within the framework of the Kohn-Sham Density Functional Theory (DFT) (^{Hohenberg & Khon, 1964};^{Khon & Sham, 1965}), applied the Full-Potential Linear Augmented Plane Wave method (FP-LAPW) and adopted the Generalized Gradient (GGA) approximation for the exchange-correlation energy (^{Perdew, et al., 1996}). The self-consistent process in the numeric package Wien2k allows the total energy calculation for constituent elements and alloys. Taking the experimental unit cell data as input, all the structures studied in this work were fully relaxed with respect to their lattice parameters and the internal degrees of freedom compatible with the space group symmetry of the crystal structure. The resulting energies versus volume functions were fitted to the equation of state by Murnaghan (^{Murnaghan, 1944}) in order to obtain de minimum energy value, the bulk modulus, its pressure derivative and the equilibrium lattice parameters and associated volume. The muffin-tin radius of the elements was 2,5; 2,19; 1,8 and 1,6 (in u.a.) Sr, Ho, Nb and O, respectively, angular momentum up to l = 10 inside the muffin-tin sphere, a maximum vector in the reciprocal space of Gmáx =12.0, R_MKAX=8, and a mesh of 1500 points in the first Brillouin zone (equivalent to a maximum of 56 k points in the irreducible Brillouin zone). Finally, the convergence criteria for the selfconsistent calculation were 0.0001 Ry for the total energies, 0.0005 u.a. in the charge and 1.0 mRy/u.a. in the internal forces. Spin polarization was included in the calculations. The thermal expansion of the crystal by the dependence of volume and the temperature on equilibrium, the Debye temperature, the specific heat at constant volume and the pressure, as well as the Grüneisen parameter as a function of temperature, were predicted from the Debye quasi-harmonic model (^{Blanco, et al., 2004}; ^{Deluque-Toro, et al., 2018}).

Results and discussion

Crystalline structure. Figure 1a shows the XRD pattern for the SHNO material, which consists of strong peaks characteristic of a primitive cubic perovskite plus a few weak line reflections arising from the super-lattice resulting in the crystallization of this material in a cubic double perovskite Fmm space group (#225) (^{Howard, et al., 2003}; ^{Madueño, et al., 2006}). No evidence of distortions from the cubic symmetry was observed in the XRD pattern. The basic perovskite composition is ABO₃, where A is a large ion suitable for the 12-coordinated cube-octahedral sites and B is a smaller ion suitable for the 6-coordinated octahedral site (^{Lufaso, et al., 2006}). Cubic complex perovskite with mixed species on a site (particularly the B site) may be represented by multiples of this formula unit and a larger unit cell, e.g., A₂BB’O₆ (^{Corredor, et al., 2011}). Thus, in the SHNO composition, the Sr⁺² with the largest ionic radius (1,13 Å) occupies position A of the cubic complex perovskite, Ho⁺³ (ionic radius 0,97 Å) and Nb⁺⁵ (ionic radius 0,70 Å) cations occupy the B and B’ positions. The ionic radii were calculated by using the SPuDs software (^{Triana, et al., 2011}). Due to the ordering of B and B’ on the octahedral site of the ABO₃ unit cell, there is a doubling in the lattice parameter on the basic cubic-perovskite unit-cell. Thus, the whole XRD pattern of SHNO can be indexed in the A₂BB’O₆ cubic structure with the cell edge a=2a_p, where a_p represents the cell lattice of the cubic perovskite. The presence of the superstructure reflection lines (311), (531), (533) and (551) in the XRD pattern of SHNO is the signature of an ordered cubic complex perovskite structure. In a substitutional solid solution A₂BB’O₆, there is a random arrangement of B and B’ on equivalent lattice positions in the crystal structure. Upon stable heat treatment, the random solid solution rearranges into a structure in which B and B’ occupy the same set of positions but in a regular way; such a structure is described as a superstructure (^{Howard, et al., 2003}).

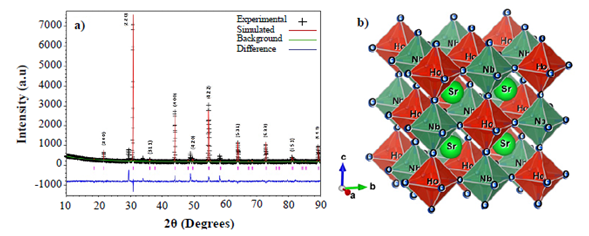
Figure 1 a) XRD pattern for the complex perovskite Sr₂HoNbO₆. Symbols represent experimental diffraction data and the base line is the difference between experimental and simulated patterns (continuous line). B) Structure of the Sr₂HoNbO₆ cubic complex perovskite constructed from the Rietveld refinement of XRD experimental data. 

In the superstructure, the position occupied by B and B’ are no longer equivalent and this feature is exhibited in the XRD pattern of the material by the presence of superstructure reflection lines. For a double cubic perovskite of the formula A₂BB’O₆ the intensity, in particular, the (111) superstructure reflection is proportional to the difference in the scattering power of the B and B’ atoms, when all the atoms are situated in the ideal position (^{Howard, et al., 2003}). A disordered arrangement of B and B’ should result in zero intensity. Therefore, ^_Ho+3 and Nb⁺⁵ cation ordering in SHNO in B and B’ positions is clearly distinguished by the presence of the significant intensity of (311), (531), (533) and (551) superstructural reflection lines. The lattice parameter of SHNO, obtained from the XRD data, was a=8,018(0) Å.

In the study and description of crystallographic structures, the concept of “positions” is fundamental (^{Wondratschek, 2006}). The so-called Wyckoff positions for this structure were experimentally determined to be Sr²⁺=8c, Ho³⁺=4a, Nb⁵⁺=4b, and O=24e. In this notation, a, b, c, and e are the Wyckoff letters that determine all the points x for which the site-symmetry groups are conjugate subgroups of the Fmm (^{Deluque-Toro, et al., 2014}). These letters constitute just a coding frame for the Wyckoff positions starting with “a” at the bottom position and continuing in alphabetical order (^{Wondratschek, 2006}). The number of equivalent points per unit cell, which accompanies the letter of Wyckoff, is known as the multiplicity of the Wyckoff position and is related to the possible coordinates. In the case of the Fmm (#225) space group, the Wyckoff letter “a” has multiplicity value of 4 and the coordinate is (0,0,0). In the same way, “b” coordinate is (½,0,0) and its multiplicity is 4. On the other hand, “c” has a multiplicity of 8 and its coordinate is (¼,¼,¼). Finally, “e” has a multiplicity of 24, with coordinate (0,2678, 0, 0).

The tolerance factor calculated from the experimental data is _τ=0.9232, which is in accordance with expected regime values for the cubic perovskite structures (^{Triana, et al. , 2015}). From the refinement analysis, the octahedral distribution in the structure of the Sr ₂ HoNbO ₆ material was constructed as shown in Figure 1b where the structure of the SHNO double perovskite constructed from the data of Rietveld refinement is shown. As expected from the discussion above, the cationic ordering of the Ho³⁺ and Nb⁵⁺ in the B and B’ sites of the cubic double perovskite can be observed clearly. On the other hand, no tilting or rotation of the HoO₆ and NbO ₆ octahedra is observed in the perfect cubic structure.

Microgranular morphology. The Secondary Electrons Image in Figure 2 for the SHNO reveals a qualitative approximation to the surface microstructure.

Figure 2 Surface microstructure of the SHNO material 

Strongly coupled particles are observed in the surface morphology, which is a characteristic of good sinterization in the polycrystalline sample. The picture evidences the formation of micrometric clusters of nanometric grains. It is clear that the grains could end up having a few tens of nm, forming groups with the appearance of clusters of several sizes in μm. The particle size D was calculated using the Scherrer equation, which is based on the widening of the maximum intensity peak of the XRD pattern due to the particle size exclusively, and defined by the ratio D=Kλ/β(θ)cosθ, where K is the Scherrer constant given by , λ=1,540598 Å is the radiation length and β(θ)=Δ(2θ) represents the halfwidening of the diffraction profile. The calculated particle size for the SHNO was D=83,2 nm. As D depends on the nucleation and growth rate, then, the value obtained for the SHNO material is attributed to the decomposition reaction toward oxides, which may be responsible of the refinement of the particle size D. Given that the solid-state reaction destroys the original morphologies of the precursor oxides, fine particles with similar size distributions can be obtained. These fine particles might be combined once and again to form agglomerates with size distributions as shown in Figure 2. Since the increase of the annealing temperature or the sintering time increases the particle size D of the material, the grain morphology changes from the common plate-like form observed in ceramics to a spherical-like form.

Magnetic response. The magnetic properties of SHNO have been investigated by measuring the DC magnetic susceptibility in the temperature range from 50 to 300 K and on the application of a 500 Oe magnetic field intensity. Figure 3 shows the temperature dependence of the inverse of the DC magnetic susceptibility as a function of temperature for SHNO.

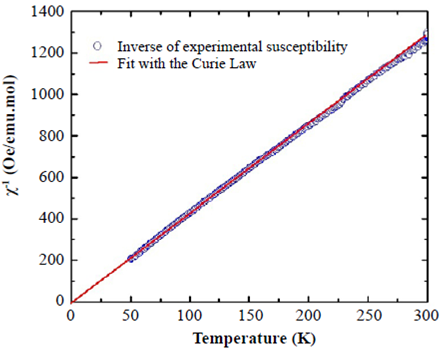
Figure 3 Inverse DC magnetic susceptibility as a function of temperature for SHNO (data points) and Curie fitting of the paramagnetic characteristic (solid line) 

The magnetic susceptibility data in this figure can be well fitted with the Curie law: χ = χ0 + C/T, where is the Curie constant, N is Avogadros’s number, ^_μeff is the effective magnetic moment ( ^_μeff = ^{_{Peff μB}} ), represents the effective Bohr magneton number, ^_μB is the Bohr magneton, ^_kB is the Boltzmann constant, and χ ₀ is the temperature independent susceptibility term. The value for this term is χ ₀ = 0.00945 emu/mol.Oe. The Curie constant, estimated from the fitting in Figure 3, is C = 12.55892 emu.K/ mol.Oe. The effective magnetic moment due to the Ho³⁺ ion, calculated from the Curie constant, is ^_μeff = 10.01 ^_μB . This value corresponds 94.4% with the expected Peff = g[J(J + 1)]^1⁄2 for an isolated Ho⁺³ cation with a 4f¹¹5d⁰6s² configuration, calculated by Hund’s rule, where g represents the Landé factor and J=S+L, S and L being the spin and orbital angular momenta. This difference may be attributed to the crystal field effects of the trivalent Ho⁺³ cation, which explain the magnetic susceptibility in SHNO.

Electronic structure. In order to obtain the most accurate results for the theoretical calculations of the density of states, we determined the optimal lattice parameters corresponding to the minimal energy value. Figure 4a shows the energy as a function of volume and the respective fitting to the Murnaghan state equation (^{Murnaghan, 1944}). Each one of the points constitutes an individual calculation and the line corresponds to a fitting with the Murnaghan state equation, carried out by using the concept of the least-square fitting method (^{Murnaghan, 1944}). The minimum of the energy was obtained for -46521,912456 Ry, the equilibrium volume was 529,147244 ų, and the volume modulus, B_o = 137,6 GPa. The theoretical value of the lattice parameter was 8,088 Å, which is 99,2% in agreement with the experimental result.

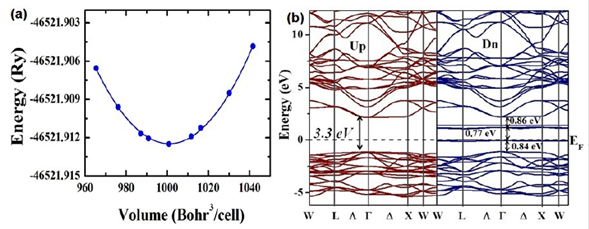
Figure 4 a) Minimization of the total energy as a function of volume for Sr₂HoNbO₆ considering the Fmm space group. b) Band structure calculated for the Sr₂HoNbO₆ by considering electronic polarization 

Figure 4b shows the band structure for both spin up and spin down configurations. E=0 eV corresponds to the Fermi level. It can be seen that these materials evidence insulator behavior with gap energy through the Fermi level from -1,3 eV up to 2,1 eV (width: 3,3 eV) for the spin-up orientation. On the other hand, for the spin-down configuration, this energy gap remains with a particular characteristic: Two isolated bands appear for E=0 eV and E=1,1 eV. In order to clarify the electronic structure of this material close to the Fermi level, we calculated the density of the states taking into account the angular momenta and spin polarization. As exemplified in Figure 5a, there is no substantial contribution of the Sr²⁺ orbitals in any of the bands, the valence or the conduction near the Fermi level. Likewise, their orbitals in the conduction band occur above E = 2,5 eV and reveal very low density values. It is clear from the results that the greatest contribution of the electronic states in the valence band is due to the 2p-O orbitals close to de Fermi level for both spin-up and spin-down polarizations. These states correspond to the bands located in the regime of energies between -5,4 eV and -1,3 eV and they define the value of the energy gap in the valence band. Moreover, as observed in Figure 5b, it is remarkable that the 4d-Nb orbitals are the biggest contributors to the states corresponding to the valence band above E=2,5 eV for the spin-up and spin-down configurations. As expected, for the characteristic of the nonmagnetic material, the 4d-Nb⁵⁺ orbitals remain in a low spin configuration, so no d_eg states in the conduction band next to the Fermi level nor any of the available states in this regime are of the d_t2g type. These states delimit the gap energy in the conduction band and their distribution is the reason why the effective magnetic moment is due solely to the contribution of the electrons 4f-Ho³⁺.

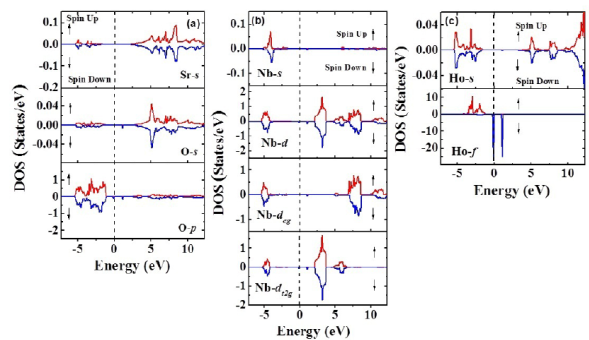
Figure 5 a) Minimization of the total energy as a function of volume for Sr2HoNbO6 considering the Fmm space group. B) Band structure calculated for the Sr2HoNbO6 by considering electronic polarization 

Finally, as shown in Figure 5c, the greatest contribution of states to the valence band was attributed to the 4f-Ho orbitals for the spin-down polarization, while there were no states available in this band for the spin-up orientation. An interesting and unusual feature is observed near the Fermi level for the 4f-Ho orbitals in the spin-down configuration; just on the Fermi level, between -0.2 eV and 0.1 eV, and above the Fermi level, between 0.9 eV and 1.3 eV, there are two peaks with high densities of states and short energies amid the energy gap. The magnetic moment obtained from the asymmetry of the calculated spin-up and spin-down density of states around the Fermi level was calculated to be 4,0 μ_B. This value corresponds to 40% when compared to that expected from the Hund’s rules for the isolated Ho³⁺ cation (^{Kittel, 1997}). This circumstance is attributed to the exchange and correlation potential applied, which do not contain corrections due to the existence of 4d-Nb orbitals. Our results are consistent with a recent report of GGA calculations for this material, with exactly the same magnetic moment value of 4,0 μ_B, attributed mostly to the contribution of the 4f-Ho³⁺ orbitals and an insulating behavior determined from calculations of the band structure and the density of states (^{Khandy & Gupta, 2018}).

Thermodynamical properties. We analyzed the effects of temperature and pressure on the thermodynamic properties of the SHNO material from the state equation under the considerations of the quasi-harmonic approximation of the Debye model as presented below. Figure 6 shows the results of specific heat at constant volume, C_V (a), and at constant pressures, C_P (b), as functions of temperature. As can be seen in the figures, the temperature was varied between 0 K and 1500 K for eight applied pressure values, from 0 to 35 Gpa. Figure 7 shows that below T=500 K for all applied pressure values, C_V≈C_P. In Figure 6(a) the trend of specific heat towards the Dulong-Petit limit, which is the specific heat value independent of temperature, is clearer than in Figure 6(b). As the temperature increases from this Dulong-Petit limit value, each of the atoms in the material absorbs the same amount of energy proportional to this temperature increase.

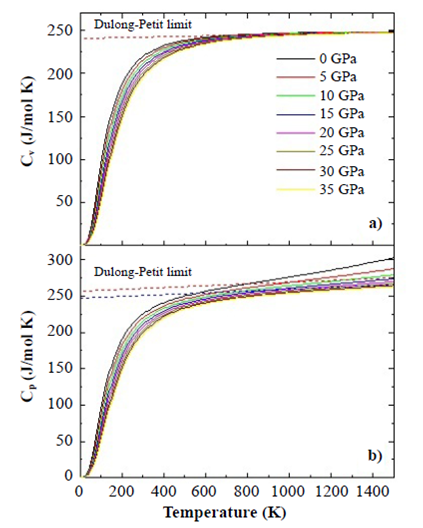
Figure 6 Specific heat C_v (a) and C_p (b) calculated by using the quasi-harmonic Debye model for the SHNO material from the Murnaghan state equation. 

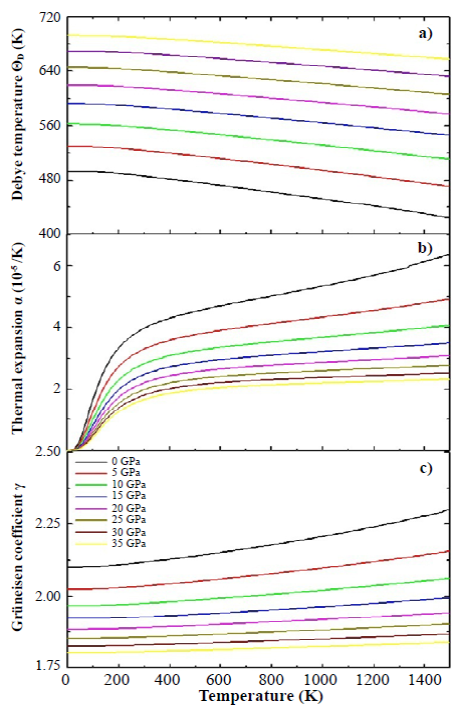
Figure 7 Debye temperature (a), thermal expansion coefficient (b), and Grüneisen coefficient (c) for the SHNO calculated by the application of the quasi-harmonic Debye model 

In Figure 7 we present the results of the calculations of the Debye temperature (a), the thermal expansion (b), and the Grüneisen coefficient (c) as functions of the temperature. We calculated the dependence of ΘD(T) (as a function of temperature) plotting isobar curves as shown in Figure 7(a). The result in Figure 7(a) shows that the Debye temperature increased substantially with increasing pressure, from 494.33 K for P = 0 GPa to 692.87 K for P=35 GPa (at T=0 K), because as the pressure increases, all the velocities of the elastic waves also increase gradually and their increase directly affects the Debye temperature. Likewise, a mild nonlinear decreasing behavior of ΘD(T) can be observed with increasing temperature for applied pressures. This decrease in the Debye temperature as a function of temperature is characteristic of perovskite-type materials (^{Anderson, 1998}). Interpreting the Debye temperature as the highest temperature that can be achieved as a result of a single normal vibration, it can be argued that the effect of pressure is the increase of cation-anion vibration frequencies while the effect of temperature is the expansive distortion of the structure, increasing the wavelength of the vibrations, decreasing the frequency and, consequently, the Debye temperature.

Figure 7(b) shows the dependence of the thermal expansion coefficient, α, with temperature and pressure. In the figure, α(T) decreases drastically with increasing pressure. On the other hand, it can be seen that at low temperatures (between 0 K and 300 K) α(T) grows rapidly with temperature, and above 300 K it grows smoothly, following an approximately linear behavior. In spite of the SHNO cubic structure, its perovskite-type character confers it an anisometric structure and, therefore, very great differences of the thermal expansion must be present along the different crystallographic directions. This behavior can be associated with the structural distortions to which the perovskitetype materials are sensitive because both temperature and pressure can give rise to inclinations and/or rotations of the HoO ₆ and NbO ₆ octahedrons, elongation of the structure in certain crystallographic directions, and eventual contractions in other directions.

Thus, the type of response in α(T) is associated with the type of distortion or transition occurring because of the application of temperature and pressure to the material. This circumstance could slightly divert any experimental results with respect to the theoretical result of Figure 7(b). On the other hand, the relatively low value of α(T) is characteristic of ceramic materials (^{Dedova, et al., 2016}).

There was an aspect that we did not consider in the calculations: as the temperature increases, structural phase transitions can occur and the material could lose its cubic structure. Finally, the Grüneisen parameter, shown in Figure 7(c), shows a gradual decrease with the increase in applied pressure (for example, from 2.10 for P=0 GPa to 1.80 for P=35 GPa, at T=0 K). This behavior was observed for all the temperatures considered in the calculations. On the other hand, the Grüneisen coefficient exhibited a smooth and non-linear increase as temperature increased. These characteristics, observed in the Grüneisen parameter as a function of pressure and temperature, are related to the alteration in the vibration frequency of a crystalline lattice according to the discussion presented above in relation to the coefficient of thermal expansion (^{Kim, et al., 2017}).

Conclusions

We obtained Sr ₂ HoNbO ₆ samples with a double cubic structure (Fmm space group) using the solid state reaction technique. Rietveld refinement of the XRD experimental data showed the occurrence of a superstructure with the presence of Ho³⁺ and Nb⁵⁺ cations interspersed along the crystallographic axes of the cell. The theoretical lattice parameters calculated from the minimization of energy with respect to the cell volume were in agreement with the experimental values determined by the Rietveld refinement of the XRD patterns. SEM images revealed the micrometric character of the granular surface with evidence of clusters constituted by nanometric crystallites. The measurements of magnetic susceptibility as a function of temperature indicated the paramagnetic feature of this complex perovskite material. The effective magnetic moment obtained from the Curie analysis of the paramagnetic behavior in curves of magnetic susceptibility as a function of temperature was 94,4% in agreement with the expected effective magnetic moment calculated from Hund rules. Calculations of the band and electronic structures suggest that this material behaves as an insulator for both spin-up and spin-down polarizations, with a gap energy of E=3,3 eV. On the other hand, an anomaly due to the 4f-Ho orbitals took place for the spindown configuration, and two intra-bands with high states/eV and a localized energy regime were observed in the middle of the gap. For this spin polarization, the band structure suggests that this material behaves as a semiconductor. The calculations of the thermodynamic properties from the state equation by means of the quasi-harmonic approximation of the Debye model showed that the effects of the interatomic vibrations gave rise to a specific heat that decreases with the applied pressure and evidenced a Dulong-Petit limit relatively high (240,63 J/mol.K) compared to other results reported for simple perovskite-type materials. Likewise, we conclude that C_V≈C_P, mainly due to the low value of the coefficient of thermal expansion. The Debye temperature showed an increasing dependence on the pressure and a decreasing one with the temperature. By contrast, both the coefficient of thermal expansion and the Grüneisen parameter decreased with the pressure and increased slightly as a function of temperature. Except for the high specificity of the Dulong-Petit heat value, the behavior observed in the thermodynamic properties was, in general, characteristic of the perovskite-like ceramic materials. We emphasize that the thermodynamic properties depend fundamentally on the value of the Grüneisen parameter, which is very sensitive both to the numerical errors in the derivation and to the smoothness of the energy equation. For this reason, it would be highly advisable to obtain experimental results of the thermodynamic properties in order to establish more objectively the microscopic mechanisms that originate them.