Introducción
La palabra "molificar" significa "suavizar" y fue introducida en la matemática en un artículo de Friedrichs (1944). Así, hacer la convolución de una función con un núcleo gaussiano se denomina molificación y ciertamente tiene un efecto suavizante o regularizador. En este artículo nos referimos a una forma específica de suavizar funciones que consiste en calcular su convolución discreta con pesos definidos a partir de una campana gaussiana truncada. Dicha convolución, denominada "molificación discreta", se puede definir en una y en dos dimensiones. El poder regularizador de la convolución con un núcleo gaussiano fue descrito por primera vez por Manselli & Miller (1980). Miller explicó su idea de molificación a su estudiante doctoral Diego A. Murio y fue este quien emprendió la tarea de utilizar la molificación en una amplia serie de problemas, pues Manselli y Miller declinaron continuar con el tema y se dedicaron a otros asuntos.
Murio (1993, 2002.) Las aplicaciones que se presentan a continuación son de desarrollo reciente y corresponden a un tema de investigación muy actual, pues la generalización del operador de molificación en dos dimensiones y la inclusión de derivadas fraccionarias en las ecuaciones abrieron un importante campo de acción a quienes trabajamos con la molificación.
El presente artículo se organizó de la siguiente manera: la primera sección se ocupa de las definiciones y las propiedades de la molificación discreta y las ilustres derivadas fraccionarias. En la siguiente sección se considera un problema inverso unidimensional de recuperación de información en la frontera de un dominio semiinfinito para una ecuación difusiva con derivada temporal fraccionaria. Se continúa con una sección centrada en un problema inverso bidimensional consistente en la identificación de un ingrediente dentro de un término fuente, también para una ecuación difusiva con derivada temporal fraccionaria, en tanto que la última sección está dedicada a la discusión y las conclusiones.
Principales operadores
En la primera parte de esta sección se define el operador de molificación discreta en una dimensión y su generalización a dos dimensiones. En la segunda parte, se introducen las derivadas fraccionarias, se explica el por qué se las llama ilustres y se consideran brevemente algunas de sus aplicaciones.
Molificación discreta unidimensional. El método de molificación es un procedimiento de filtrado basado en la convolución con un núcleo gaussiano truncado que sirve para regularizar problemas mal condicionados y para estabilizar y evitar oscilaciones ficticias en la discretización de ecuaciones diferenciales parciales por medio de esquemas explícitos.
Sea
 una función discreta, por ejemplo, evaluaciones o promedios de una función real y = y(x), definida en una malla de puntos equidistantes
una función discreta, por ejemplo, evaluaciones o promedios de una función real y = y(x), definida en una malla de puntos equidistantes
donde x0 y h son reales y h es positivo. La molificación de esta función discreta es la convolución
donde η es el parámetro de soporte y los factores de ponderación o pesos satisfacen
Para calcular los pesos se utiliza un núcleo gaussiano truncado que se construye con base en dos números reales positivos, p y ( que satisfacen la igualdad
 El núcleo es
El núcleo es
donde la constante de normalización
 es tal que
es tal que
 . El núcleo tiene soporte compacto, pues es cero fuera del intervalo [-p(,p(]. En adelante suponemos que p = 3. El número p determina el soporte del núcleo y el número ( se encarga de la forma de la campana gaussiana, mientras mayor es ( más aplanada es la campana. Los pesos se definen asi:
. El núcleo tiene soporte compacto, pues es cero fuera del intervalo [-p(,p(]. En adelante suponemos que p = 3. El número p determina el soporte del núcleo y el número ( se encarga de la forma de la campana gaussiana, mientras mayor es ( más aplanada es la campana. Los pesos se definen asi:
 , donde
, donde
 . Nótese que estos pesos son independientes de h pues i
. Nótese que estos pesos son independientes de h pues i
 es decir, los pesos no dependen del parámetro del discretización especial, ya que
es decir, los pesos no dependen del parámetro del discretización especial, ya que
La tabla 1 muestra una lista de pesos.
Tabla 1 Pesos de molificación
| η | ω0 | ω1 | ω2 | ω3 | ω4 | ω5 |
|---|---|---|---|---|---|---|
| 1 | 8,43E+03 | 7,86E+02 | ||||
| 2 | 6,04E+03 | 1,93E+03 | 5,44E+01 | |||
| 3 | 4,56E+03 | 2,38E+03 | 3,33E+02 | 1,21E+01 | ||
| 4 | 3,63E+03 | 2,40E+03 | 6,94E+02 | 8,73E+01 | 4,73E+00 | |
| 5 | 3,00E+03 | 2,26E+03 | 9,67E+02 | 2,34E+02 | 3,21E+01 | 2,48E+00 |
La Figura 1 ilustra la suavización que genera la molificación cuando se aplica a una función ruidosa. Más precisamente, sea
La función f y su molificación, que denotaremos Jf aparecen en la primera gráfica de la figura 1. Por otro lado, sea ( > 0 y sea f una aproximación de f ( que cumple ǀǀf f ε ǀǀ∞ ≤ ε. La función aproximada se denomina "ruidosa", pues se obtiene sumando a cada punto un número aleatorio distribuido uniformemente en el intervalo [-(, (]. A una tal distribución de números aleatorios se le conoce como "ruido" gaussiano.
En la segunda gráfica de la Figura 1 aparecen f ( y Jf(. El código MATLAB utilizado para generar las dos funciones f y f ( para s = 0.1, es el siguiente:
f = @(x) 2*x.*(x < 0.5 & 0 < x) + (2-2*x).*(0.5 < x & x< 1); x = linspace(-.2,1.2);
fx = f(x);
epsil = 0.1;
fep = fx + (2*rand(size(x))-1)*epsil;
Algunos ejemplos de problemas mal condicionados en los que se puede trabajar con molificación son los inversos de difusión (Mejia & Murio, 1996; Murio, 2007; Murio & Mejía, 2008a; Mejía & Piedrahita, 2017) y los inversos de identificación de modelos (Mejia & Murio, 1995; Murio & Mejía, 2008b; Mejía, et al., 2011; Acosta, et al., 2014; Acosta, et al., 2015; Echeverry & Mejía, 2018).
La mayoría de las veces trabajamos con funciones definidas en intervalos, lo cual hace que la definición de molificación, por ser una convolución, no se pueda usar en algunos puntos vecinos de los extremos del intervalo. Esta dificultad se discute en el trabajo de Acosta & Mejía (2008), en el que se definen las llamadas condiciones de borde, las cuales consisten en modificaciones del operador de molificación para esos puntos limítrofes. A pesar del éxito de tales modificaciones, este es un aspecto de la molificación que aún requiere más estudio.
A manera de conclusión podemos decir que la molificación es una buena alternativa como método de regularización. Además, es una herramienta para hacer menos estrictas las condiciones de estabilidad del tipo Courant-Friedrichs-Lewy (CFL), que esperamos que siga vigente por un buen tiempo. Este uso de la molificación se puede consultar en Acosta, et al. (2012, 2014, 2015).
Las propiedades de aproximación de la molificación discreta se pueden consultar en Acosta & Mejía (2014). Hay aspectos de la molificación que requieren profundización, por ejemplo, las condiciones de borde y la escogencia de los parámetros ( o n, que sería deseable hacer de forma automática según cuán perturbados estén los datos que se van a molificar.
Existen otras versiones del método de molificación, por ejemplo, las de Garshasbi & Dastour (2015), Hao (1994), Li & Fu (2011) y Shi, et al. (2016), las cuales se diferencian en la implementación, pero, en todos los casos, se trata de métodos basados en convolución que son útiles para la regularización de problemas mal condicionados.
Hay pocas referencias de molificación bidimensional. Entre las mencionadas arriba, solamente en el estudio de Li & Fu (2011) se aborda un problema con dominio en una franja de
 2, pero se utiliza solamente la molificación unidimensional. El tema de la molificación en dos dimensiones se trata en la siguiente sección.
2, pero se utiliza solamente la molificación unidimensional. El tema de la molificación en dos dimensiones se trata en la siguiente sección.
Molificación discreta bidimensional. El propósito de esta sección es presentar una generalización a dos dimensiones del operador de molificación unidimensional introducido en la sección anterior. El operador bidimensional de molificación discreta que definiremos enseguida fue introducido por Acosta & Bürger (2012). Sin embargo, debe advertirse que la molificación bidimensional se está realizando por lo menos desde los años 90 (Zhan & Murio, 1999; Zhan, et al., 2001).
Nuestro dominio es una malla uniforme bidimensional del plano
 2 dada por
2 dada por
 , donde h y k son los reales positivos que determinan tamaños de paso en cada dirección. Para una función G, definida en esta malla como G (x
i
,, yi) = Gij, se establece su molificación discreta como
, donde h y k son los reales positivos que determinan tamaños de paso en cada dirección. Para una función G, definida en esta malla como G (x
i
,, yi) = Gij, se establece su molificación discreta como
 donde η determina el soporte discreto y los pesos ω
j
son los de la molificación unidimensional. Nótese que
donde η determina el soporte discreto y los pesos ω
j
son los de la molificación unidimensional. Nótese que
donde los dos operadores
 y
y
 corresponden a la molificación unidimensional ya definida.
corresponden a la molificación unidimensional ya definida.
Las propiedades de aproximación de este operador aparecen en Acosta & Bürger (2012) y en Echeverry (2018). Para las propiedades del operador de molificación bidimensional definido en la década de los 90 por el grupo liderado por Murio, recomendamos consultar Zhan & Murio (1999).
Otro aspecto del método de molificación que ha suscitado mucho interés recientemente es el de las derivadas fraccionarias, las cuales se definen en la siguiente sección.
Derivadas fraccionarias. El estudio de las derivadas fraccionarias se denomina cálculo fraccional y sus orígenes se remontan a fines del siglo XVII. Importantes matemáticos de distintas épocas, como Leibniz, L'Hópital, Johann Bernoulli, Euler, Abel, Riemann y Liouville, han contribuido al establecimiento de esta teoría. La calificación de estas derivadas como "ilustres" se justifica por la nómina de matemáticos destacados que ha ayudado a su nacimiento y evolución. Asimismo, nos atrevemos a afirmar que también son ilustres por el lugar destacado que ocupan en la matemática aplicada y porque estamos seguros de que su protagonismo aumentará en los próximos años. En el campo del cálculo fraccional sugerimos consultar a Oldham & Spanier (2006), Miller & Ross (1993), Podlubny (1999), Diethelm (2010) y Guo, et al. (2015).
Recientemente, la investigación en cálculo fraccional se ha intensificado, pues hay evidencia de que varios modelos matemáticos mejoran cuando se cambian las derivadas usuales por las fraccionarias.
En el caso específico de difusión en un medio poroso y con fracturas, Fomin, et al. (2010) han establecido mediante experimentos que la difusión en el medio es anómala y que en lugar de las tradicionales leyes de Fick, es conveniente recurrir a ecuaciones de difusión con derivadas fraccionarias.
En el campo del modelamiento matemático de materiales viscoelásticos, se está encontrando que es preferible un modelo fraccional que uno con derivadas enteras (Diethelm, 2010).) La regla general es que si el proceso bajo estudio tiene propiedades asociadas con la memoria o la herencia, es útil intentar un modelo fraccional en lugar de uno tradicional.
A continuación definimos dos de las derivadas fraccionarias más conocidas. El orden de derivación en ambos casos es un número real positivo a.
Derivada fraccionaria de Caputo. Para una función real f suficientemente suave, la derivada de Caputo de orden α es
donde el entero m cumple m - 1 < α ≤ m y
 exp(-x)dx es la función gamma, que es una generalización del factorial, pues si n es un entero positivo, Γ(ri) = (n - 1)!
exp(-x)dx es la función gamma, que es una generalización del factorial, pues si n es un entero positivo, Γ(ri) = (n - 1)!
Derivada de Riemann-Liouville. Sea f una función real continua a trozos en (0,∞), integrable en cualquier subintervalo finito de (0,∞). Entonces para t > 0, la integral fraccionaria de Riemann-Liouville de orden α de f es
Para definir la derivada fraccionaria de Riemann-Liouville de orden a, utilizamos el entero m tal que m - 1 ≤ a ≤ m y tomamos λ = m - α. La derivada fraccionaria de Riemann-Liouville de orden a de f es
El siguiente lema advierte sobre cuán distintas pueden ser las derivadas fraccionarias.
Lema 1. Para funciones constantes, la derivada fraccionaria de Caputo es cero y en cambio la derivada fraccionaria de Riemann-Liouville no es cero. Dem: tomemos 0 < α < 1, m = 1 y f (t) = 1 para todo t. Debido a la presencia de la derivada en el integrando, la derivada fraccional de Caputo de orden α de f es 0. En cambio, la derivada de Riemann-Liouville de orden a de f es la función
Una anotación pertinente en este momento es: las derivadas de orden entero dependen del comportamiento "local" de la función y las derivadas fraccionarias se calculan con base en los valores de la función a todo lo largo del dominio de definición. Eso hace que a los operadores del cálculo fraccionario se les denomine operadores "no locales" o "con memoria".
Problema inverso de advección-dispersión con derivada temporal fraccionaria
El objetivo es estudiar la aplicación de la molificación como método de regularización para la solución del siguiente problema inverso: reconstrucción de la concentración de soluto en la frontera del dominio físico que es unidimensional semiinfinito. La derivada fraccionaria se toma en el sentido de Caputo y los coeficientes de advección y de dispersión son constantes. La información adicional que se requiere para enunciar correctamente el problema inverso y poderlo resolver consiste en una distribución de datos perturbados correspondientes a la concentración y al flujo en un punto interior del dominio para todo tiempo.
La configuración es unidimensional, lo cual significa que estamos ante una primera aproximación, tal como lo explican Benson, et al. (2000), de quienes citamos unas líneas que son pertinentes: "Una pregunta típica que se hace un hidrogeólogo que estudia el transporte de un contaminante es: ¿qué tan lejos y qué tan rápido avanzará el contaminante? Como primera aproximación, la mayoría de problemas de esta naturaleza se reducen a una ecuación unidimensional de advección-dispersión".
Advertimos que nos proponemos estudiar la solución numérica del problema inverso por molificación discreta y no consideramos el problema matemático de existencia y unicidad de soluciones.
Problemas directo e inverso. Enunciamos un problema inverso a partir del siguiente problema directo:
y se trabaja con la hipótesis adicional u(x, t) acotada para x → ∞. La variable u representa la concentración del soluto, u
x
es el flujo de dispersión, y las constantes positivas a y d representan la velocidad promedio del fluido y el coeficiente de dispersión, respectivamente. De ahora en adelante, a la derivada de Caputo
 la denotamos como
la denotamos como
 . El problema inverso de interés es:
. El problema inverso de interés es:
La información adicional consiste en las medidas interiores en x = 1 para la concentración y el flujo de dispersión. Para hacer realista la situación, suponemos que la información adicional no se conoce exactamente y sus aproximaciones p
(
y 0
(
satisfacen los estimados
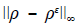
 , donde ( representa el máximo nivel de perturbaciones en los datos.
, donde ( representa el máximo nivel de perturbaciones en los datos.
Se trata de un problema mal condicionado según el siguiente teorema.
Teorema 1. Aproximar ξ y ( a partir de la ecuación diferencial y las mediciones interiores adicionales p ( y 0 s es un problema gravemente mal condicionado en las componentes de alta frecuencia.
Dem: proponemos solamente un esbozo. Suponemos que todas las funciones dependientes del tiempo con las que trabajamos se pueden extender a toda la recta real. Aplicamos la transformada de Fourier con respecto a t y llegamos al sistema
La variable en el espacio de frecuencias es

 donde
donde

 . Además,
. Además,

 Además,
Además,
 con
con
 . Se cumple que si | ω| → ∞, entonces
. Se cumple que si | ω| → ∞, entonces

Y
 donde se concluye el mal condicionamiento anunciado (Mejía & Piedrahita, 2017).
donde se concluye el mal condicionamiento anunciado (Mejía & Piedrahita, 2017).
La molificación y la derivada fraccionaria. La presencia de la derivada dentro de la integral en la derivada fraccionaria de Caputo anuncia la posibilidad de un problema mal condicionado cuando los datos no se conocen exactamente. Seguimos a Murio (2008) para el esquema implícito de discretización de la derivada fraccionaria y a Murio & Mejía (2008b) para la combinación de la derivada fraccionaria con la molificación.
Lema 2. Sea g una función continuamente diferenciable. Consideremos la cuadratura con parámetro de discretización temporal k de la derivada de Caputo de g dada por la fórmula
donde
 denota la función parte entera opiso,
denota la función parte entera opiso,
 y
y

Entonces esta cuadratura satisface la aproximación de primer orden
Dem: Ver Murio (2008).
El problema estabilizado por molificación se define para las variables
 y es el siguiente:
y es el siguiente:
Enseguida se enuncia un esquema de diferencias finitas con sentido de marcha en la dirección del espacio. Esta es una técnica que ha probado su efectividad en la solución de problemas inversos (Murio, 2002; Mejía, et al., 2011; Mejía & Murio, 2008a; Mejía & Murio, 2008b; Garshasbi & Dastour, 2015).
Los parámetros de discretización son: números reales positivos k, h y números enteros positivos N, M tales que Nk = T es el tiempo final y Mh = 1. La malla espacial es x = (mh)m=0…„ M y el vector de instantes de tiempo es t = (nk) n=0,…N . Denotamos R m n ,W m ny y Q m n a las aproximaciones calculadas para la concentración de soluto v(mh, nk), el flujo molificado vx(mh, nk) y la derivada temporal fraccionaria de la concentración de soluto D t a v(mh, nk) respectivamente. El esquema con sentido de marcha en la dirección espacial es el siguiente:
donde m = M, M- 1, 1 y n = 1, N. Las aproximaciones buscadas son
 y
y
 para n = 1, …,N.
para n = 1, …,N.
Para poder calcular con este esquema es indispensable un método numérico de solución del problema directo en [0,1] pues esa es la forma de obtener los datos de inicio. De esto se ocupa la próxima sección.
Generación de los datos para la solución numérica del problema directo. Lo usual es que no se disponga de solución exacta para el problema directo. De hecho, en las industrias y talleres es muy frecuente que se enuncien problemas inversos y se resuelvan en el computador debido a la imposibilidad de medir en una de las fronteras, o en el interior del equipo con el que se está trabajando, por ejemplo, una caldera o una turbina.
El problema directo de advección difusión con derivada temporal fraccionaria asociado al problema molificado es
Para este problema directo se enuncia un método implícito de solución por diferencias finitas que tiene en cuenta el método de aproximación de la derivada fraccionaria del Lema 2. Los detalles se pueden consultar en Mejía & Piedrahita (2017).
Teorema 2 (Convergencia)
La aproximación de la concentración obtenida con el esquema de marcha en la dirección espacial para la frontera activa x = 0, converge a la concentración exacta cuando el paso temporal y el tamaño de las subdivisiones espaciales tienden a cero.
Experimento numérico. El experimento consiste en la recuperación de una concentración con forma de paso unitario. Más precisamente, la concentración en la frontera izquierda (por identificar) es la función
y la concentración en la frontera derecha es w
1
(t) = 0. Los errores absolutos de la Tabla 2 se obtuvieron con la norma RMS (root mean square), que se define así: x = (x, x,… x
n
) si entonces RMS(x) es la raíz cuadrada de la media aritmética de los cuadrados de los x
j
. La Figura 2 ilustra la calidad de la identificación. Se obtuvo con los parámetros de discretización
 .
.
Tabla 2 Reconstrucción de u(0,t) con ruido máximo s = 0,05
| h | k | Error absoluto, | Error absoluto, |
|---|---|---|---|
| α = 0,5 | α = 0,9 | ||
| 1/50 | 1/128 | 0,0875 | 0,1256 |
| 1/50 | 1/256 | 0,0754 | 0,1051 |
| 1/100 | 1/128 | 0,0958 | 0,1216 |
| 1/100 | 1/256 | 0,083 | 0,1054 |
| 1/100 | 1/512 | 0,0809 | 0,0982 |
En la Tabla 2 se presenta un informe de resultados numéricos para dos valores de α. Sirve para observar la dependencia del error de los parámetros de discretización h y k y, por lo tanto, para verificar el teorema de convergencia. Nótese que la concentración en el borde x = 0 es una función de t y que los errores son menores para los menores valores del parámetro de discretización temporal k.
Problema inverso de identificación de término fuente
En esta sección presentamos los resultados obtenidos para un problema inverso de identificación de término fuente en una ecuación de difusión en la que la derivada temporal es fraccionaria en el sentido de Caputo y la configuración espacial es bidimensional.
El problema directo. El problema directo de difusión de interés para nosotros corresponde al seguimiento de la concentración de un contaminante en un acuífero en el que la dispersión o difusión es dominante y, por lo tanto, no se tiene en cuenta la advección. El término fuente de la ecuación cumple la regla de variables separables en la que el factor dependiente de espacio es la magnitud o intensidad de la descarga del contaminante y el factor dependiente del tiempo es un coeficiente de atenuación. El término de dispersión o difusivo es un operador diferencial denotado con la letra L y se explica más adelante. El problema directo de valor inicial y valores en la frontera son
donde
 es su clausura, la derivada temporal fraccionaria es en el sentido de Caputo, la difusión es
es su clausura, la derivada temporal fraccionaria es en el sentido de Caputo, la difusión es
y los coeficientes en L satisfacen las siguientes relaciones:
 .
.
Con estas condiciones el operador -L es simétrico y uniformemente elíptico, definido en
 .
.
El problema inverso. Nos interesa identificar el factor f(z) en el término fuente, lo cual exige que tengamos alguna información adicional. En nuestro caso se trata de la distribución espacial de la concentración u(z,T) = q(z) en el interior del dominio para un tiempo futuro T. Más aun, suponemos que la información adicional es una medición y está sujeta a errores. Por lo tanto, en lugar de la distribución exacta q disponemos de una aproximación q
s
que cumple con
 .
.
Existencia de la solución. Obtenemos de Ma, et al. (2018) y Sakamoto & Yamamoto (2011) una expansión en serie para la solución del problema directo. Está basada en las funciones propias del operador -L y en la función de Mittag-Leffler de dos parámetros positivos α y ( dada por
Nótese que esta función es una generalización de la función exponencial. Denotemos por
 las funciones propias de
las funciones propias de
 a sus valores propios. Además, denotamos (.,.) al producto interno en L2 (Ω). La solución del problema directo es
a sus valores propios. Además, denotamos (.,.) al producto interno en L2 (Ω). La solución del problema directo es
Denotemos
 . Entonces,
. Entonces,
 es decir, sus coeficientes de Fourier son
es decir, sus coeficientes de Fourier son
 . Para
. Para
 definimos el espacio
definimos el espacio
Es un espacio de Hilbert con la norma


Para la solución del problema inverso definimos el operador
y buscamos una función f
£
que minimiza al funcional Hf=

Teorema 3
Supongamos que p
 C([0,T\) y satisface p(t) ≥ p
0
> 0 para todo t
C([0,T\) y satisface p(t) ≥ p
0
> 0 para todo t
 [0,T]. Supongamos además
[0,T]. Supongamos además
 y existen
y existen
 tales que
tales que
 . Entonces
. Entonces
donde C1 es una constante que puede depender de α, T, λ 1 y la medida del dominio ( (Ω). Además, ô es el parámetro de molificación asociado con η.
Dem: la solución está dada por
El método numérico. La solución del problema inverso se realiza con diferencias finitas y requiere de la solución del problema directo. El método implícito utilizado está descrito en Mejía & Piedrahita (2018), pero no tiene todavía un sistema eficiente de condiciones de borde para la molificación bidimensional, aspecto en el que estamos trabajando todavía. Por tal razón, la medida de errores en el experimento que presentamos enseguida, se realiza sobre puntos interiores de la malla. Los puntos fronterizos y los inmediatamente siguientes se dejan por fuera en el cálculo del error. Utilizamos la norma RMS.
El experimento numérico en el que se basan las figuras siguientes consiste en la ecuación diferencial fraccional
donde
 está dado por
está dado por
 , con α11 (x, y) = x2 + 1, α22 (x, y) = y2 + 1, p(t) = 1 + exp(-(t + α)), y el ingrediente por identificar es fix, y) = sin 3πx sin 3πy. El dominio Ω es un rectángulo unitario y T = 1. Como parámetros de discretización usamos h = 1/32 tanto en x como en y y k = 1/10 en tiempo. El máximo nivel de ruido en los datos es ( = 0,05.
, con α11 (x, y) = x2 + 1, α22 (x, y) = y2 + 1, p(t) = 1 + exp(-(t + α)), y el ingrediente por identificar es fix, y) = sin 3πx sin 3πy. El dominio Ω es un rectángulo unitario y T = 1. Como parámetros de discretización usamos h = 1/32 tanto en x como en y y k = 1/10 en tiempo. El máximo nivel de ruido en los datos es ( = 0,05.
En primer lugar, en la Figura 3 se ilustra la importancia de incluir la molificación para lograr un método estable. En segundo lugar, en la Figura 4 se ilustra la calidad de la identificación que se logra con una adecuada molificación.
Por último, en la Tabla 3 se presentan los resultados de otros experimentos que sirven para verificar la convergencia del algoritmo. Los errores en la identificación de f se calculan con la norma RMS.
Discusión y conclusiones
En este artículo verificamos la utilidad de los operadores de molificación en aplicaciones a problemas inversos en una y dos dimensiones basados en ecuaciones difusivas en las que la derivada temporal es fraccionaria. También expusimos argumentos para justificar el apelativo de "ilustres" para las derivadas fraccionarias. Creemos haber establecido que las derivadas fraccionarias serán cada vez más importantes en la matemática aplicada y que la molificación discreta es un método de regularización adecuado para resolver problemas inversos en los que esas derivadas participan.
Seguiremos intentando ayudar en el desarrollo de este campo de investigación de análisis numérico, con especial énfasis en el estudio de ecuaciones diferenciales fraccionarias en las que las derivadas fraccionarias están en las variables espaciales. Asimismo, aspiramos a mejorar el operador de molificación bidimensional en lo que respecta a las condiciones de borde. Por último, nos proponemos enfrentar problemas inversos basados en ecuaciones difusivas no lineales en las que hay derivadas fraccionarias. Recientemente, consideramos ecuaciones de advección-dispersión con término fuente no lineal y derivada temporal fraccionaria (Mejía & Piedrahita, 2019), y el plan es continuar explorando este tema y enfrentar nuevos problemas en el futuro inmediato.


















































