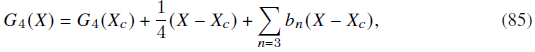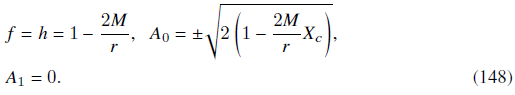Introducción
Pese a que el modelo estándar cosmológico ACDM es compatible con las observaciones (Aghanim, N., et al, 2020), éste no logra darle una explicación física consistente a los problemas de la cosmología moderna como lo son la actual expansión acelerada del universo (energía oscura) (Riess, A. G., et al, 1998; Perlmutter, S., et al, 1999) y la existencia de materia oscura (Bertone, G. & Hooper, D., 2018). Debido a esto y en un intento por explicar físicamente el problema del sector oscuro, se han construido gran cantidad de teorías que modifican la gravedad. Una de las ramas más importantes de estas teorías es aquélla que comprende todos los modelos en los cuales se asume la presencia de un campo acoplado de forma no mínima con la gravedad que puede ser escalar (Deffayet, C., et al, 2011; Nicolis, A., et al, 2009; Deffayet, C., et al, 2009a, 2009b; Horndeski, H. W.,, 1974; Deffayet, C., & Steer, D., 2013; Gleyzes, J. et al, 2015; Crisostomi, M., et al, 2017; Ben Achour, J., et al, 2016; Crisostomi, M., et al, 2016; Langlois, D., & Noui, K., 2016), vectorial (Heisenberg, L., 2014; Tasinato, G., 2014a, 2014b; Allys, E., et al, 2016a, 2016c; Beltrán Jiménez, J., & Heisenberg, L., 2016; Rodríguez, Y., & Navarro, A., 2017; Heisenberg. L., et al, 2016; Gallego Cadavid, A., & Rodríguez, Y., 2019; Kimura, R., et al, 2017; Allys, E., et al, 2016b; Beltrán Jiménez, J., & Heisenberg, L., 2017) o tensorial (de Rham, C., et al, 2011; Hinterbichler, K., 2012; de Rham, C., 2014; Hassan, S. F., & Rosen, R. A., 2012; Hinterbichler, K., & Rosen, R. A., 2012; de Rham, C. & Gabadadze, G., 2010). Este gran número de teorías existentes ofrece una amplia variedad en cosmología, brindándonos herramientas para poner a prueba y descartar aquellas teorías que no sean compatibles con las observaciones.
Un candidato natural para atacar el problema del sector oscuro es un campo escalar acoplado de forma no mínima a la gravedad (Deffayet, C., et al, 2011; Nicolis, A., et al, 2009; Deffayet, C., et al, 2009a, 2009b; Horndeski, H. W.,, 1974; Deffayet, C., & Steer, D., 2013; Gleyzes, J. et al, 2015; Crisostomi, M., et al, 2017; Ben Achour, J., et al, 2016; Crisostomi, M., et al, 2016; Langlois, D., & Noui, K., 2016); sin embargo, las teorías basadas en esta idea (teorías escalar-tensor) han sufrido fuertes restricciones a raíz de la observación de la onda gravitacional GW170817 y su contraparte electromagnética GRB 170817A (Abbott, B. P., et al, 2017b, 2017a, 2017c; Baker, T., et al, 2017; Creminelli, P. & Vernizzi, F., 2017; Sakstein, J. & Jain, B., 2017; Ezquiaga, J. M. & Zumalacárregui, M., 2017; Wang, H., et al, 2017; Kase, R. & Tsujikawa, S., 2019). Otra alternativa (teorías vector-tensor) surge de acoplar de forma no m nima un campo vectorial a la gravedad, lo que es motivado, en particular, por la existencia de campos de gauge en el Modelo Estándar de la física de partículas como campos mediadores de las interacciones fundamentales. Un aspecto que parece ser negativo concerniente al uso de campos vectoriales es el hecho de que éstos generan anisotropía en la expansión del universo, lo cual no los erige como candidatos naturales para dar cuenta del fenómeno de la energía oscura; no obstante, esta característica podría, naturalmente, explicar aquellas anomalías relacionadas con una posible dirección privilegiada en dicha expansión (Cai, R. G., et al, 2013; Rodrigues, D. C., 2008; Beltrán Jiménez, J. & López Maroto, A., 2007; Campanelli, L., et al, 2006). Un caso particular de estas teorías vector-tensor es el de la teoría generalizada de Proca (o teoría de Galileones vectoriales) (Heisenberg, L., 2014; Tasinato, G., 2014a, 2014b; Allys, E., et al, 2016a, 2016c; Beltrán Jiménez, J., & Heisenberg, L., 2016; Rodríguez, Y., & Navarro, A., 2017) en la cual la acción se construye a partir del campo vectorial y su primera derivada de tal manera que tanto las ecuaciones de campo de la teoría completa como las de la respectiva teoría en el límite de desacoplamiento contienen derivadas de orden no mayor a dos. Lo anterior impide el desarrollo de la conocida inestabilidad de Ostrogradski (Ostrogradski, M., 1850; Woodard, R. P., 2007; Woodard, R. P, 2015).
Así cómo sucedió con las teorías escalar-tensor, es necesario hacer uso de las observaciones de los fenómenos astrofísicos para determinar la factibilidad de las teorías vector-tensor. Una de las alternativas empleadas últimamente para este fin ha sido el estudio de las soluciones de agujeros negros, en vista de las recientes observaciones de ondas gravitacionales (Abbott, B. P., et al, 2017b, 2017a, 2017c; Abbott, R., et al, 2020). Esto se debe a que estas últimas transportan información acerca de los objetos que las producen, lo que permite conocer más sobre la física de los agujeros negros y los alrededores de los mismos así como comparar las características de estas ondas con aquéllas predichas por las diferentes teorías de gravedad para estos objetos astrofísicos. Dicho enfoque ya ha sido recientemente explorado en las teorías escalar-tensor mediante el análisis perturbativo de las soluciones de agujeros negros (Kobayashi, T., et al, 2012, 2014; Ganguly, A., et al, 2018) y el cálculo de los modos quasinormales de las ondas gravitacionales provenientes de este tipo de objetos (Tattersall, O. J. & Ferreira, P. G., 2018; Dong, R., et al, 2017). También se ha explorado la estabilidad de la respectivas soluciones en las teorías vector-tensor, en especial en la teoría generalizada de Proca (Kase, R., et al, 2018; Heisenberg, L., et al, 2018).
En este trabajo se han encontrado, como primera aproximación y con base en el artículo de la Ref. (Heisenberg, L., et al, 2017), soluciones exactas de agujeros negros estáticos y esféricamente simétricos en la teoría generalizada de Proca. Esto se llevó a cabo, en primer lugar, determinando las ecuaciones de campo gravitacional y de campo vectorial de la teoría. Posteriormente se determinó el perfil de la métrica y del campo vectorial acoplado a la gravedad para cada acoplamiento presente en la acción generalizada de Proca. Finalmente se establecieron las condiciones necesarias para obtener soluciones exactas para cada tipo de acoplamiento.
Teoría generalizada de Proca
Considérese, en primer lugar, un espaciotiempo plano. Es sabido que cualquier vector, debido al teorema de Helmholtz, puede expresarse como la suma de una parte sin divergencia y una sin rotacional de la siguiente manera:
con Aμ, siendo la parte sin divergencia y ϖ, siendo un campo escalar que se identifica con el grado de libertad longitudinal asociado a . Aμ. Entonces, si se desea que las ecuaciones de campo, tanto para Aμ como para su componente longitudinal ϖ no sean de orden superior a dos, con el fin de evitar la inestabilidad de Ostrogradski (Ostrogradski, M., 1850; Woodard, R. P., 2007; Woodard, R. P, 2015), la acción del campo vectorial puede incluir, únicamente, al campo mismo y a sus primeras derivadas espaciotemporales ∂ μ A V (Rodríguez, Y., & Navarro, A., 2017).
Para construir la acción de la teoría generalizada de Proca (o acción de Galileones vectoriales) (Rodríguez, Y., & Navarro, A., 2017; Heisenberg, L., 2014; Beltrán Jiménez, J., & Heisenberg, L., 2016; Allys, E., et al, 2016a, 2016c; Tasinato, G., 2014a, 2014b) se deben identificar, en primer lugar, todos los posibles invariantes de Lorentz construidos a partir de la contracción de campos vectoriales y derivadas espaciotemporales de primer orden con los invariantes primitivos del grupo de Lorentz SO(3,1): el tensor métrico y el tensor de Levi-Civita. Una vez se han identificado estos términos, se agrupan en una combinación lineal general. A continuación, se establecen relaciones entre los coeficientes de la combinación lineal de tal manera que no se propaguen más de tres grados de libertad, en consonancia con la estructura del grupo de Poincaré, lo cual se establece mediante la ligadura primaria proveniente de la condición Hessiana H 0v = 0 (Heisenberg, L., 2014; Errasti, V., et al, 2020a, 2020b), en donde
Como último paso, se realiza el reemplazo A μ → ∂ μ ϖ y se remueven los términos cuya acción resultante no corresponda a la de un Galileón escalar (o acción de Horndeski (Deffayet, C., & Steer, D., 2013; Nicolis, A., et al, 2009; Horndeski, H. W.,, 1974; Deffayet, C., et al, 2009a, 2009b)).
De todo lo anterior resulta que la acción para el Galileón vectorial que generaliza la acción Abeliana de Proca es
en donde (Beltrán Jiménez, J., & Heisenberg, L., 2016; Allys, E., et al, 2016c)
siendo =
 , en donde ε
μvpσ
es el tensor de Levi-Civita.
, en donde ε
μvpσ
es el tensor de Levi-Civita.
La versión para espacio tiempo curvo se obtiene promoviendo las derivadas parciales a derivadas covariantes y añadiendo los contratérminos requeridos para evitar la aparición de derivadas de orden mayor a dos en las ecuaciones de campo asociadas al modo longitudinal (Deffayet, C., et al, 2009a). De esta forma se obtiene (Heisenberg, L., 2014; Tasinato, G., 2014a, 2014b; Allys, E., et al, 2016a, 2016c; Beltrán Jiménez, J., & Heisenberg, L., 2016; Rodríguez, Y., & Navarro, A., 2017)
en donde g es el determinante de la métrica, F ≡ -F μv F μv /4,y
siendo X = -A μ A μ /2, R el escalar de Ricci, G μv el tensor de Einstein, G í,x ≡∂ G í /∂X,y L μvpσ - es el tensor doble dual de Riemann
Soluciones exactas de agujeros negros estáticos y esféricamente simétricos
Se emplearán a continuación las ecuaciones de campo gravitacional y vectorial de la teoría generalizada de Proca presentadas en el apéndice. Se empleará, además, el siguiente ansatz para la métrica y el campo vectorial de la teoría en coordenadas (pseudo)esféricas:
Estos perfiles para los campos son compatibles con un espaciotiempo estático y esféricamente simétrico.
Solución de Reissner-Nordström en Relatividad General
Como preparación, en primer lugar, se usará el acomplamiento
en donde m p es la masa reducida de Planck, el cual conduce a las siguientes ecuaciones de campo vectorial y gravitacional, respectivamente,
en donde la única componente diferente de cero para el tensor de esfuerzos, para el perfil estático esféricamente simétrico, es la siguiente:
En la expresión anterior y en las subsiguientes, una prima significa una derivada con respecto a r.
Así, las ecuaciones de campo no triviales obtenidas son
Si se multiplica la ecuación (23) por (hf) -1 y se suma a la ecuación (24) se obtiene como resultado
y, al considerarse un comportamiento asintóticamente plano es claro que f (r ) = h (r ) = 1 cuando r →ꝏ por lo tanto const. = 1 y
Posteriormente, al reemplazar (27) en la expresión (22) se llega a la ecuación diferencial
la cual tiene como solución
en donde P y Q son constantes de integración. Luego, sustituyendo las ecuaciones (27) y (29) en la ecuación (23) se obtiene que la función métrica f es
en donde Q es la carga asociada al campo vectorial y -2M es la constante de integración que, una vez se lleva al límite Newtoniano, se identifica como la masa del agujero negro. La solución obtenida es, por lo tanto, la de Reissner-Nordström:
Estas soluciones satisfacen también la ecuación (25) ya que usando la condición (27), y posteriormente las soluciones (31) y (32), se obtiene la ecuación
la cual se satisface idénticamente.
Sumado a todo lo anterior, cabe resaltar que la componente longitudinal A 1 corresponde a un modo de gauge no físico ya que este valor está indeterminado por las ecuaciones (22)-(25). Asimismo, la constante P es una constante arbitraria sin significado físico alguno.
Campo masivo de Proca
También cabe revisar el campo masivo de Proca en Relatividad General, el cual está dado por las funciones
en donde μ es la masa del campo vectorial.
Las ecuaciones de campo gravitacional y vectorial para esta configuración están dadas por
las cuales llevan al siguiente sistema de ecuaciones diferenciales para los perfiles de la métrica y el campo vectorial que se están teniendo en consideración:
A partir de la ecuación (38), y observando que μ ≠ 0, se tiene que A 1 = 0, lo que implica que la ecuación (42) se satisface idénticamente. Reemplazando A 1 = 0 en las ecuaciones (39) y (40) y sumándolas se llega a la expresión
que al multiplicar por h -2 se convierte en
Considerando el comportamiento asintótico del lado izquierdo de esta expresión se sabe que, con el fin de que r h sea el horizonte de eventos, f → 0 y h → 0 cuando r → r h . Es necesario también que f (r) > 0 y h(r) > 0 para r >r h con el objetivo de que la métrica sea Lorentziana. Debido a esto, las funciones métricas se pueden expandir alrededor del horizonte de la forma
por lo tanto, si r → r h , el lado izquierdo de la ecuación (45) tiende a un valor finito en tal límite. Asimismo, al analizar el comportamiento del lado derecho, se requiere que A° tienda a cero con el fin de que la expresión sea consistente. De otra parte, considerando el comportamiento asintótico para r →∞, se sabe que en este límite f = h = 1. De esta manera, el límite de la expresión (44) conduce a
y siendo μ ≠ 0 se concluye que A 0 → 0 cuando r → ∞.
Ahora bien, para determinar el comportamiento predicho por la ecuación (37) para valores de r » r h , se reescribe esta ecuación empleando la expresión (45):
Ya que A 0 se hace muy pequeño para r » r h , se descartan los términos cuadráticos de éste obteniéndose así la ecuación diferencial
cuya solución es
siendo c 1 y c 2 constantes de integración. De otra parte, teniendo en cuenta que la ecuación (47) predice que A 0 (r → ∞) = 0, la ecuación (49) conduce a
Este comportamiento comienza a ser dominante cuando r>
 . Además, debido a que se debe tener que A
0
→ 0 cuando r → ∞, se concluye que μ = 0. Por lo tanto no hay solución de agujero negro estático y esféricamente simétrico para un campo vectorial de Proca debido a que dicha solución existe solamente si μ = 0, reduciéndose así a la solución de Reissner-Nordström.
. Además, debido a que se debe tener que A
0
→ 0 cuando r → ∞, se concluye que μ = 0. Por lo tanto no hay solución de agujero negro estático y esféricamente simétrico para un campo vectorial de Proca debido a que dicha solución existe solamente si μ = 0, reduciéndose así a la solución de Reissner-Nordström.
Soluciones exactas para el acoplamiento cuártico G 4
Para este caso se considera el acoplamiento
el cual reduce las ecuaciones de campo a las expresiones
en donde la simetrización se define como

La forma explícita de estas ecuaciones, para la configuración del campo y métrica que se está estudiando, es la siguiente:
En primer lugar, la ecuación (60) admite una solución en donde A 0 = 0 o A 1 = 0. Por lo tanto, considerando A 0 = 0 y A 1 ≠ 0, la ecuación (56) establece la siguiente relación entre las funciones métricas:
Entonces, al reemplazar esta relación en la ecuación (58) se obtiene:
lo que inevitablemente lleva a la inconsistencia A 1 = 0. En segundo lugar, si se considera A 0 ≠ 0 y A 1 = 0, el sistema de ecuaciones diferenciales tiene solución únicamente si A 0 = 0, lo que resulta, de nuevo, en una inconsistencia. La conclusión es que tanto A 0 como A 1 son iguales a cero y, por lo tanto, la solución es de tipo Schwarzschild.
Ahora bien, si se considera la rama en la cual A 0 y A 1 son diferentes de cero, de la ecuación (60) se obtiene la relación (61). Reemplazando esta relación y su derivada en la ecuación (58) se obtiene
Al reemplazar esta expresión en las ecuaciones (55) y (57) y resolver el sistema, se obtiene la solución dada por
en donde P, 2M y Q son constantes de integración. De otra parte, dado que en el límite r →ꝏ se debe tener espaciotiempo plano, se deduce que C = 1. Insertando estas expresiones en (61) y (63) se obtiene la solución
Por consiguiente, las soluciones para el presente acoplamiento cumplen las siguientes condiciones:
con X c constante, las cuales serán usadas de aquí en adelante con el fin de encontrar soluciones exactas. Esta última condición se traduce en que
En contraste, para un acoplamiento general G 4 = G 4 (X), las ecuaciones de campo vectorial están dadas por
Para que la última expresión se satisfaga existen dos posibilidades, A 1 = 0 y ≠ 0, que serán estudiadas a continuación.
A1 ≠ 0
Al proponer que la segunda derivada del acoplamiento G 4 evaluada en X c cumpla la condición
se observa que la ecuación (73) establece la siguiente relación entre las funciones métricas h y f:
de la cual, haciendo uso de la condición (69), se obtiene que la función métrica f viene dada por
Dicha solución lleva a que la ecuación (72) se reduzca a la expresión
cuya solución ya fue obtenida previamente. Esta solución es
la cual, a causa de la condición (70), lleva a que la componente longitudinal del campo tenga la forma
Así, insertando las expresiones de f, h, A 0 y A 1 en la ecuación de campo gravitacional de componente (μ,v) = (0,0),
se obtiene
De manera análoga, realizando el mismo procedimiento anterior en la ecuación de componente (μ, v) = (1,1),
y reemplazando (81) en la misma, se logra determinar el valor de X c en términos de las constantes de integración. Este valor es
Esto último indica que la función que describe a la componente longitudinal del campo está dada por
De lo anterior se infiere que la función G 4 (X), que obedece a las condiciones (74) y (81), está dada por
en donde X c = P2/2 y todas las b n son constantes. El modelo G 4 (X) = m 2 p /2 + X/4 es el caso especial de la última expresión (85), es decir, G 4 (X c ) = m 2 p /2 + X c /4 y todos los b n = 0 para n ≥ 3. La solución de arriba es una solución de Schwarzschild con componente vectorial longitudinal diferente de cero.
Aunque la carga P en un espaciotiempo de Reisner-Nordströmno tiene significado físico, en este caso es una carga que controla el perfil longitudinal A i (r), mas no su geometría. Nótese que se puede apagar la carga Q y dejar la carga P encendida en presencia de un agujero negro masivo, caracterizando así un perfil longitudinal no trivial. En este sentido, P representa una carga adicional para la configuración, además de la masa y la carga eléctrica. Sin embargo, esta carga no es observable aplicando la ley de Gauss -ya que el campo no contribuye a F μv - y por lo tanto, estrictamente hablando, esta configuración no viola la conjetura de no pelo (Carter, B., 1971; Robinson, D. C., 1975).
A 1 = 0
Si se impone A 1 = 0 y la condición (70), se tiene que A2 0, = 2fX c a partir de (71). Bajo la condición (69), la ecuación (73) se anula y la ecuación (72) se reduce a
Si se toma 1 - f - rf' = 0, su solución
no satisfaría la ecuación (86). Entonces, se debe considerar
con G 4 ,x (X c ) = 0. Escribiendo a la función métrica f como
la ecuación (88) se transforma en una nueva ecuación diferencial para la función λ (r ), la cual es
Esta expresión se puede reescribir como
cuya solución, ∀M <r, es
en donde C 2 y C son constantes. En consecuencia, la función f queda representada por la siguiente expresión:
en donde M = C 2 . Además, se deduce que C = 1 ya que la función métrica debe tendera cuando r →∞. Así,
Con todo lo anterior, al usar la ecuación de campo gravitacional de componente (μ, v) = (0,0), se tiene que
Este resultado implica, adicionalmente, que las ecuaciones de campo resultantes se satisfagan idénticamente. Así, se tiene que un acoplamiento G 4 (X) que cumpla todo lo anterior debe ser de la forma
La solución exacta resultante es, por lo tanto,
en donde
 . Esto corresponde a una solución de agujero de Reissner-Nordström con una carga eléctrica igual a la masa del agujero negro.
. Esto corresponde a una solución de agujero de Reissner-Nordström con una carga eléctrica igual a la masa del agujero negro.
Soluciones exactas de agujeros negros para acoplamientos generales
Se procede ahora con la deducción de soluciones exactas de agujeros negros en la presencia de los acoplamientos G 3 (X), G 5 (X), G 6 (X), g 5 (X) y G 2 (X, F) = -2g 4 (X) F. Este último corresponde al modo vectorial intrínseco que fue originalmente introducido en ℒ 4 en la forma g4(X)( ∇ p A σ ∇ p A σ -∇ p A σ ∇ σ A p ), en donde g4(X) = const * G 4X . Para este análisis se toma en cuenta el término de Einstein-Hilbert, es decir, G 4 (X) = m2 p/2. De manera similar a lo realizado en las secciones anteriores, se imponen las condiciones (69) y (70) en el desarrollo siguiente.
Acoplamiento cúbico G 3 ( X)
Para este caso, la ecuación de campo vectorial de componente α = 1 es
la cual da paso a dos posibilidades: G 3,x (X C ) = 0 y G 3 x(X C ) ≠ 0.
(i) G 3,X (Xc ) = 0
Para este caso, las ecuaciones para el campo vectorial Ao y las de campo gravitacional de componentes (μ, v) = (0,0) y (μ, v) = (2, 2) son, respectivamente,
Ya que la ecuación de componente(i,v) = (1,1) es igual a la de componente (i,v) = (0,0), siendo las demás triviales.
A partir de la solución a la ecuación (99), la cual fue obtenida en secciones anteriores, se concluye que la componente en dirección temporal del campo está dada por
en donde P y Q son constantes de integración. Adicionalmente, si inserta este resultado en la ecuación (100), se obtiene la expresión
cuya solución para fviene dada por
Por lo tanto, para este caso se tiene una solución de Reissner-Nordström con la componente longitudinal del campo diferente de cero gracias a la condición (7 ):
Por consiguiente, una función que lleve a esta solución debe estar dada por
en donde los b n son constantes.
(ii) G 3,X (Xc) ≠ 0
Combinando las expresiones (69), (70) y (98) se obtiene
Sustituyendo esta expresión en la ecuación de campo vectorial para α = 0 se obtiene rA' 0 ' + 2A'0 = 0, lo cual lleva a la solución A 0 = P + Q/r con dos constantes P y Q. Entonces, insertando esta solución en la ecuación (107) se obtiene
en donde C es una constante. Para satisfacer que la métrica sea asintóticamente plana, f debe tender a 1 cuando r →∞, lo que conduce a que P
2 = 2Xc. Así las ecuaciones de campo gravitacional se satisfacen únicamente si C = 0 y P =
 . Ademas, de la ecuación de componente (μ,v) = (0,1) se tiene que A1 = 0. Entonces, para M = ±Q/(
. Ademas, de la ecuación de componente (μ,v) = (0,1) se tiene que A1 = 0. Entonces, para M = ±Q/( ) se obtiene la solución (94) con el modo A
1
igual a cero.
) se obtiene la solución (94) con el modo A
1
igual a cero.
Acoplamiento de quinto orden G 5 (X)
Para este acoplamiento, las ecuaciones de campo vectorial de componentes α = 0 y α = 1 vienen dadas por
Aplicando la condición (70) en ambas ecuaciones, multiplicando la ecuación (109) por 2 A 1 f y restándola de la ecuación (110) multiplicada por A 0 , se obtiene la ecuación diferencial
Adicionalmente, la ecuación (110), bajo la condición (70), adopta la forma
De la ecuación (111) se obtiene, por supuesto, que A 0 = P + Q/r, con P y Q constantes. Si la ecuación (112) se satisface para (i) A 0 A' 0 = X c f ' o (ii) A 2 0 = 2 fX c
Para la primera rama se tiene la expresión
cuya integración da como resultado
con M = -PQ/(2Xc). En el límite asíntotico cuando r →∞, se debe tener que f = h = 1, lo cual indica que C = 1. De otra parte, se tiene que las ecuaciones de campo gravitacional de componentes (μ, v) = (0,0), (μ, v) = (1,1) y (μ, v) = (2,2) son, respectivamente,
Insertando la solución para A 0 y para f en la ecuación de componente (μ, v) = (2,2) se obtiene que
Lo anterior lleva a que se satisfagan idénticamente las ecuaciones de componentes (μ, v) = (0,0) y (μ, v) = (1,1). Por lo tanto las soluciones para este tipo de acoplamiento están dadas por
lo cual, usando la condición (70), conlleva a
La existencia de esta solución requiere que 2M 2 m 2 p >Q2.
A partir de la ecuación (70), la segunda rama corresponde a A 1 = 0. El reemplazar esta condición en la ecuación (109) conduce a
la cual es la misma ecuación diferencial (88) cuya solución es
Por otra parte, dela ecuación(118) se tiene que
lo que indica que la expresión para la componente temporal del campo vectorial, Ao, está dada por
con la relación particular Q2 = 2M 2 m 2 p . De hecho esto puede ser visto como el caso de las soluciones de la rama anterior con la componente radial del campo siendo nula.
Es de anotar que un modo concreto de obtener las soluciones ya presentadas es mediante un acoplamiento G 5 (X) que esté descrito por la siguiente expresión:
en donde X c = m 2 p .
Acoplamiento de sexto orden G 6 ( X)
En presencia del acoplamiento general G 6 , la ecuación de campo vectorial de componente α = 1 se reduce a
para la cual se requiere que A 1 = 0 o A’0 = 0.
(i) A’0 = 0
En este caso se tiene que
lo que implica que la componente α = 0 de la ecuación de campo vectorial y la componente (μ, v) = (0,1) de la ecuación de campo gravitacional se satisfagan idénticamente. De esta manera, las ecuaciones de campo gravitacional de componentes (μ, v) = (0,0) y (μ, v) = (1,1) llevan a la ecuación diferencial
cuya solución, obtenida previamente, es
la cual también hace que la ecuación de campo gravitacional de componente (μ, v) = (2,2) se satisfaga idénticamente. Por lo tanto, usando la condición (70), se obtiene que el modo longitudinal del campo vectorial viene dado por
Ya que A
1
→±
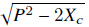 cuando r →∞, se requiere que P2
> 2X
c
para garantizar la existencia de la solución.
cuando r →∞, se requiere que P2
> 2X
c
para garantizar la existencia de la solución.
0.0.1 (ii) A 1 = 0
Para este caso, en primer lugar, la ecuación de campo gravitacional de componente (μ, v) = (0,1) se satisface idénticamente. Además, debido a la condición (70), A0 = 2fXc. Esto lleva a que las ecuaciones de campo gravitacional de componentes (μ, v) = (0,0) y (μ, v) = (1,1) se reduzcan, respectivamente, a
Para obtener soluciones exactas se tomarán las condiciones
De la ecuación (134) se obtiene la solución de Reissner-Nordström cuya carga es igual a la masa del agujero negro, es decir,
que al reemplazar en la ecuación (133) da como resultado que X
c
= m
2
P
. Además, la componente temporal del campo vectorial es A
0
= P + Q/r, en donde P = ±
 y Q =
y Q =
 . Esto es equivalente a la solución obtenida para el acoplamiento de quinto orden G
5
(X) de la rama A
2
0
= 2 fX
c
.
. Esto es equivalente a la solución obtenida para el acoplamiento de quinto orden G
5
(X) de la rama A
2
0
= 2 fX
c
.
Un modelo concreto que lleve a la solución obtenida para este caso debe ser de la forma
en donde X c = m 2 p .
Acoplamiento cuártico g 4 (X)
Considérese el acoplamiento dado por
en donde g 4 (X) es una función de X. De esta manera, la ecuación de campo vectorial de componente α = 1, usando las condiciones (69) y (70), es
Considérese ahora, por lo tanto, el caso en el cual se satisface la relación
En estas circunstancias, la ecuación de campo vectorial de componente α = 0 y la ecuación de campo gravitacional de componente (μ, v) = (0,0) son, respectivamente,
A partir de la primera ecuación, la componente temporal del campo vectorial es
la cual, al reemplazar en la segunda ecuación, lleva a
con el modo longitudinal del campo dado por la expresión (71). Esto equivale a un solución de Reissner-Nordström con carga efectiva Q
e
f f = Q
 que es diferente de Q a menos que g4(Xc) = 0.
que es diferente de Q a menos que g4(Xc) = 0.
Así, un acoplamiento que lleve a estas soluciones viene dado por
Para el caso particular g 4 (X c ) = 1/2 se obtiene la solución de Schwarzschild f = h = 1 - 2M/r con A0 indeterminado.
Por otra parte, la ecuación (139) también se satisface si (i) A 1 = 0 o (ii)A’ 0 = 0. Para la rama (i), la ecuación de campo vectorial de componente α = 0 y la ecuación de campo gravitacional de componente (μ, v) = (0,0) vienen dadas, respectivamente, por
Existe una solución exacta bajo las condiciones g 4 x (X c ) = 0 y g 4 (X c ) = 1/2 la cual está dada por
Esta solución existe para la función (145) con g 4 (X c ) = 1/2.
Para la rama (ii), se obtiene la solución de Schwarzschild f = h = 1 - 2M/r con A 0 = const. y A i dado por la ecuación (71) para acoplamientos generales g 4 (X).
Acoplamiento vectorial de quinto orden g 5 (X)
Finalmente, se busca la solución exacta para el acoplamiento de quinto orden g5 (X). Para este acomplamiento, la ecuación de campo vectorial de componente a = 0 viene dada por
Para la rama A’0 = 0, se obtiene la solución de Schwarzschild f = h = 1 - 2M/r seguida del modo longitudinal del campo dado por la ecuación (71), con A0 = const, para acoplamientos g 5 (X) generales.
Para la otra rama, fg 5 = (A2, - 2 fX c )g 5 x, existe solución exacta bajo la condición
Esto lleva a que la ecuación de campo vectorial de componente α = 0 y la ecuación de campo gravitacional de componente (μ, v) = (0,0) sean las de la solución de Reissner-Nórdstrom en Relatividad General. De esta manera se obtiene la solución de Reissner-Nordstróm con A 1 dado por la ecuación (71).
Ya que g 5 (X c ) = 0, un acoplamiento de quinto orden de la forma
da como resultado, en este caso, la solución de Reissner-Nordstróm con el modo longitudinal diferente de cero.
Conclusiones
En este trabajo se hizo uso de la acción (9) y a partir del método variacional se obtuvieron las ecuaciones de campo gravitacionales y vectoriales de la teoría generalizada de Proca. Posteriormente, se determinaron los perfiles del campo y del tensor métrico propios de un espaciotiempo estático y con simetría esférica. Con ello se establecieron condiciones para las funciones métricas y las funciones componentes del campo vectorial con el fin de obtener soluciones exactas. También se calculó la forma que deben tener los acoplamientos para llegar a dichas soluciones.
En primer lugar, al usar el acoplamiento G 4 = m 2 p /2, se recuperó la Relatividad General para un espaciotiempo de electrovacío. En éste se obtuvo la solución de Reissner-Nórdstrom. Por otra parte, se corroboró la no existencia de soluciones en el caso de Proca masivo. La no existencia se da como consecuencia de que la solución para el campo vectorial es incompatible con el comportamiento asintótico que deben tener las funciones métricas, tanto en el horizonte de eventos (f(r h ) = h(r n ) = 0) como en el infinito (f (r → ∞) = h(r → ∞) = 1). La incompatibilidad desaparece cuando la masa del campo ¡¡ es nula, lo cual corresponde a un espaciotiempo de Reissner-Nordström.
Seguidamente se encontró la solución para el acoplamiento G 4 = m 2 p /2 + X/4. Para esta solución se satisfacen las condiciones f = h y X = X c = const., las cuales se usaron para encontrar soluciones exactas correspondientes a cada tipo de acoplamiento usado. En general, las soluciones obtenidas para todos los acoplamientos considerados en este documento no difieren de soluciones de Schwarzschild y Reissner-Nordström salvo en las funciones componentes del campo vectorial. Esto, en efecto, es consecuencia de las restricciones usadas con el objetivo de encontrar soluciones exactas. Entonces, el aliviar las condiciones puede conducir a soluciones más generales mediante métodos iterativos. Adicionalmente, en varias de las soluciones encontradas en este trabajo, el modo longitudinal del campo vectorial resultó ser diferente de cero con lo cual aparece una nueva carga P que no rompe la conjetura de no pelo dado que en las funciones métricas no se evidencia la presencia de esta carga. Sumado a esto, la carga P aparece como un modo de gauge no físico en la componente temporal del campo. Por otra parte, aunque se obtienen diversas expresiones para la componente longitudinal del campo vectorial, en los demás acoplamientos estudiados en este documento, las funciones métricas siguen siendo soluciones de Schwarzschild o Reissner-Nordström.
Es claro que al usar una teoría y obtener resultados que ya son predichos por una teoría más simple, se tiene mayor preferencia por esta última. En este caso, al usar la teoría generalizada de Proca, que es de mayor complejidad que la Relatividad General, se obtiene soluciones exactas que ya son predichas por esta última. Por consiguiente, en el marco de las soluciones exactas de agujeros negros estáticos y esféricamente simétricos, la teoría de Einstein luce más atractiva que la teoría generalizada de Proca.