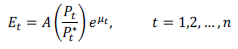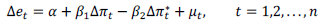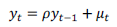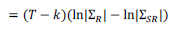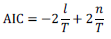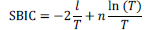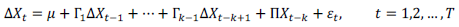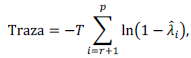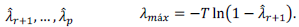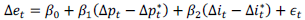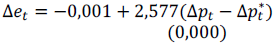1. Introducción
La teoría de la paridad del poder de compra (PPP, por sus siglas en inglés) fue planteada en principio por el economista sueco Gustav Cassel en el año 1920. Esta teoría representa una síntesis de los trabajos de Wheatley (1807) y Ricardo (1821) y se hizo popular en los años setenta con el tipo de cambio flexible, en especial por los avances econométricos para las series no estacionarias (Chocholata, 2001). El análisis de la PPP establece que en el largo plazo el tipo de cambio entre dos monedas debe ser igual a la relación de los niveles de precios en los dos países para que un producto cualquiera tenga el mismo precio en ambos países, pero expresado en términos de la misma moneda (Shams & Murad, 2010). Por otro lado, la PPP es interpretada también como el comovimiento del tipo de cambio y el nivel de precios relativo de dos países y la versión de corto plazo de la PPP es el comovimiento de las variables en el corto plazo y su dinámica en busca del equilibrio (Chocholata, 2001; Kim, 2008).
Perú es una economía pequeña y abierta al mundo que depende fuertemente de las transacciones con sus socios comerciales, en especial con Estados Unidos. Esto conlleva una exposición a shocks de tipo internacional, como los registrados en 2006 por el diferencial de tasas de interés en activos internacionales, o en 2008 por la crisis financiera mundial, que generaron condiciones de volatilidad en el tipo de cambio peruano. En este sentido, una característica común de los países que experimentaron shocks internacionales es el rechazo de la PPP en el largo plazo, pues esta funciona como un mecanismo de ajuste del mercado de capitales trasladando cualquier desalineamiento de la economía al tipo de cambio (Guevara, 1999; Jaramillo y Serván, 2012).
Así pues, el objetivo principal de esta investigación fue contrastar la validez de la PPP entre Perú y Estados Unidos para el período 2000-2019. Al respecto, se mencionan algunos trabajos a nivel internacional que verifican la validez de la PPP; entre ellos se encuentra el trabajo pionero de Frenkel (1978). Este autor desarrolla la teoría de la PPP y, además, verifica que para Francia y Reino Unido el tipo de cambio causa en sentido de Granger los precios, reportando que las políticas empleadas sobre el tipo de cambio tienen efectos sobre los precios en una economía. Años más tarde, Frenkel (1981), en su trabajo sobre la PPP para el Reino Unido, analizó la relación entre el tipo de cambio y los precios domésticos; y reportó las paridades de la PPP pueden ser modeladas por un proceso autorregresivo de primer orden. Además, indicó que los tipos de cambio y el cumplimiento de la PPP son de importancia para la realización de políticas. Por otro lado, Pacheco (2017) evaluó la PPP para Perú, Chile y Colombia y encontró evidencia para algunos períodos de baja y mediana volatilidad. Kugler y Lenz (2014) reportaron el cumplimiento PPP para las monedas: libra, lira, corona noruega, chelín austríaco, escudo y peseta; además, se rechaza la PPP para el dólar estadounidense, dólar canadiense, corona danesa y franco belga. Gómez y Rodríguez (2012) reportaron el cumplimiento de la PPP para las economías de México y Estados Unidos. Asimismo, Muñoz (2011) verificó el cumplimiento de PPP para los países de Asia y de América Latina y encontró que la condición de PPP es rechazada y que es posible que esta se cumpla en un horizonte de tiempo más amplio. Shams y Murad (2010) reportaron para Bangladesh el rechazo de la PPP e indicaron que para ese país la teoría de la PPP puede ser usada con tipo de cambio fijo. Kim (2008) aplicó las técnicas de cointegración para verificar la PPP de largo plazo para las monedas de Italia, Francia, Japón y Reino Unido y encontró el cumplimiento de la PPP. Sideris (2004), en su trabajo para validar la PPP en el largo plazo para las monedas dólar estadounidense, marco alemán y yen japonés, utilizó la metodología de Johansen yencontró una relación de largo plazo de la PPP para Estados Unidos y Alemania y también para Estados Unidos y Japón, lo que evidencia que la política monetaria de Estados Unidos es transmitida a los precios de Alemania y Japón. Para el caso de México, Macías (2003) reportó el cumplimiento de la PPP en el largo plazo. Chocholata (2001) utilizó la metodología de Johansen y Engle-Granger para verificar la PPP para Latvia y Eslovaquia y encontró que ambas metodologías no confirman la validez de la PPP en los casos analizados. Para el caso de España, Italia, Francia, Reino Unido, Alemania y Estados Unidos, Pérez y Vega (1993) reportaron evidencia del cumplimiento de la PPP con la metodología de Johansen en un contexto multivariado. Edison (1987) en su trabajo para el tipo de cambio dólar/libra, con un mecanismo de corrección de error para Reino Unido y Estados Unidos, reportó que la relación de la PPP no representa de manera adecuada el tipo de cambio dólar/libra.
Luego de esta introducción, el resto del documento se organiza de la siguiente manera: en la sección dos se explica el marco teórico que sustenta el trabajo; en la sección tres la presenta la metodología econométrica empleada para la estimación y contraste; en la sección cuatro se realiza la especificación del modelo de la PPP en sus versiones absoluta y relativa; en la sección cinco se muestran los resultados de la estimación de las formas funcionales; y, por último, en la sección seis, se presentan las conclusiones más importantes del presente estudio.
2. Marco teórico
La PPP es un modelo utilizado para verificar la condición de paridad internacional de dos monedas en el largo plazo. Fue desarrollada inicialmente en principio por Frenkel (1976) con sus orígenes conceptuales en la teoría cuantitativa del dinero desarrollada por David Ricardo (Ricardo, 1821). La PPP, a diferencia de la ley de un solo precio, establece que el nivel de precios de dos países debe igualarse cuando se expresan en la misma moneda y, se representa con la siguiente relación de paridad:
donde E es el tipo de cambio, P es el nivel de precios de la economía doméstica y P * el nivel de precios de la economía extranjera, todos evaluados en un período t=1,2,…n. La ecuación (1) también se puede escribir como
donde μ t es el término de error estocástico con media cero que captura todas las desviaciones de la PPP. Aplicando logaritmos a la ecuación (2) se tiene la relación lineal siguiente:
donde las variables en minúsculas representan las variables transformadas a logaritmo. La relación de la PPP presenta dos versiones: la versión absoluta y la relativa. La versión absoluta de la PPP en la ecuación (3) establece como hipótesis de largo plazo valores α=0, β 1 =β 2 =1, equivalente a la hipótesis nula de eficiencia de mercados en el largo plazo. Esta versión absoluta de la PPP es una hipótesis muy fuerte y pocas veces es considerada por los economistas en su análisis, debido sobre todo a que, para que sea correcta esta versión, los precios de ambos países deben ser medidos en una canasta de bienes similares, lo que resulta solo en países con desarrollo similar. Por esta razón, diversos trabajos desarrollan la versión relativa de la PPP. Esta versión de la PPP ya no considera los niveles de precios; en su lugar resalta la relación entre las tasas de inflación y el tipo de cambio. Esta versión se expresa como
donde Δx t =x t -x t-1 describe la primera diferencia de la variable x t para el período t=1,2,...,n. La ecuación (4) indica que si la inflación Δp t en la economía doméstica es mayor que la inflación en la economía extranjera Δp * , el tipo de cambio aumenta en una cantidad igual a la diferencia de las tasas de inflación. Para la versión relativa de la PPP dada en la ecuación (4), la hipótesis nula de eficiencia del mercado cambiario establece que α=0 y β 1 =β 2 =1. Al reescribir la ecuación (4) para Δp t =π t y Δp * =π * , donde π y π * son las tasas de inflación doméstica y extranjera, se tiene la ecuación siguiente:
Por otro lado, la PPP en su versión relativa podría no cumplirse, en especial, por la existencia de una mayor volatilidad del tipo de cambio respecto de los precios y también por la composición de las canastas de consumo de los países. Luego, si el tipo de cambio y las tasas de inflación de los países convergen en el largo plazo, la condición de homogeneidad de precios se cumple, esto es β 1 =β 2 ; por consiguiente, si la PPP en su versión relativa se cumple, entonces la ecuación (5) se puede expresar en términos de brechas como
De este modo, para que el mercado cambiario sea eficiente en el largo plazo debe cumplirse α=0 y β=1, que representa la PPP en su forma relativa.
3. Metodología
La teoría de la PPP indica que las series no estacionarias se conectan mediante una relación con el término de error estacionario, es decir son cointegradas como lo definen Engle y Granger (1987). En el presente trabajo se testea la validez de la PPP utilizando la metodología de Johansen (Johansen, 1988; Johansen y Juselius, 1990) para verificar en principio el cumplimiento de la relación de largo plazo entre las series económicas y, acto seguido, verificar los parámetros para el cumplimiento de la PPP en su versiones absoluta y relativa. A continuación se presenta la metodología y las pruebas estadísticas necesarias para el desarrollo del documento.
3.1 Prueba de raíz unitaria de Dickey-Fuller aumentada
La prueba de Dickey-Fuller aumentada (ADF) busca determinar de la existencia o no de raíces unitarias en una serie de tiempo (Dickey y Fuller, 1979). La hipótesis nula de esta prueba es que existe una raíz unitaria en la serie. En un modelo simple autorregresivo de orden uno, AR(1):
donde y t es la variable de interés, t es el de tiempo, ρ es un coeficiente, y μ t es el término de error. La raíz unitaria está presente si ρ=1. En este caso, el modelo resulta no ser estacionario. El modelo de regresión puede ser escrito como:
donde Δ es el operador de primera diferencia. Este modelo puede ser estimado y las pruebas para una raíz unitaria son equivalentes a pruebas δ=0 (donde δ=ρ − 1). Dado que la prueba se realiza con los datos residuales en lugar de los datos en bruto, no es posible utilizar una distribución estándar para proporcionar valores críticos. Por lo tanto, esta estadística tiene una determinada distribución conocida simplemente como la tabla de Dickey y Fuller (1979).
3.2 Prueba de raíz unitaria de Phillips-Perron
La prueba de raíz unitaria de Phillips-Perron (P-P) es una prueba de raíz unitaria utilizada en el análisis de series de tiempo para probar la hipótesis nula de que una serie de tiempo no es estacionaria (Phillips y Perron, 1988). Se basa en la prueba ADF de que la hipótesis nula es ρ=0 en y t =ρy t- 1+μ t , donde Δ es la primera diferencia del operador. Al igual que la prueba ADF, la prueba P-P aborda la cuestión de que el proceso de generación de datos para podría tener un orden superior de autocorrelación que es admitido en la ecuación de prueba, lo que hace y t- 1 endógeno e invalida así el Dickey-Fuller t-test. Mientras que la prueba ADF aborda esta cuestión mediante la introducción de retardos de Δy t como variables independientes en la ecuación de la prueba, la prueba P-P hace una corrección no- paramétrica a la estadística t-test.
3.3 Retardos óptimos
Uno de los contrastes más habituales en un modelo de vectores autorregresivos (VAR) es número de retardos que deben incluirse como variables explicativas. Hay que tener en cuenta que en cada ecuación entra un bloque de retardos de todas las variables del vector; por esto, el número de parámetros que serán estimados crece muy rápido con el número de retardos. Sin embargo, una estrategia razonable consiste en incluir el menor número de retardos que permita eliminar la autocorrelación del término de error. El contraste formal de significación de un conjunto de retardos que utiliza un estadístico de razón de verosimilitud está dado por
donde |Σ R | y |Σ SR | describen los determinantes de las matrices de covarianzas de los modelos restringidos y sin restringir, respectivamente. Asimismo, para hallar el orden del modelo VAR es necesario examinar los criterios de información que son determinados sobre el valor muestral de la función logaritmo de verosimilitud. Los más conocidos son el criterio de información de Akaike (AIC, por sus siglas en inglés), criterio de información de Schwartz (SBC, por sus siglas en ingles) y el Criterio de Información de Hannan-Quinn, dados por
Siendo
 k el número de variables y n=k (d+pk) el número de parámetros estimados en el modelo VAR con que es el número de variables exógenas, p el orden del VAR. Estos estadísticos se calculan para una sucesión de modelos con distinto número de retardos y se comparan, seleccionando aquel modelo que produce el menor valor del estadístico respectivo.
k el número de variables y n=k (d+pk) el número de parámetros estimados en el modelo VAR con que es el número de variables exógenas, p el orden del VAR. Estos estadísticos se calculan para una sucesión de modelos con distinto número de retardos y se comparan, seleccionando aquel modelo que produce el menor valor del estadístico respectivo.
3.4 Cointegración de Johansen
Para realizar la prueba de cointegración de Johansen es necesario que todas las variables económicas sean integradas de orden uno, es decir I(1) entonces, el siguiente paso es encontrar evidencia de una relación de largo plazo, llamada también cointegración, usando la metodología de Johansen1, que definió un modelo VAR con k retardos en el proceso :
siendo ε t el término de error Gausiano p-dimensional con media cero y matriz de varianza Λ, X t un vector de variables I(1) y μ un vector de constantes. Debido a que X t es no estacionaria, la ecuación (7) puede ser expresada en un modelo de corrección de error en primeras diferencias
donde Γ i =-(I-Π1-…-Π i ),i=1,2,…,k-1 y Π=-(I-Π1-…-Π k ). La matriz de coeficientes Π contiene información respecto del largo plazo entre las variables en el vector de base de datos. Si el rango de Π es igual a p, es decir la matriz tiene rango completo, el vector X t es estacionario. Si el rango de Π es igual a cero, la matriz es una matriz nula y la ecuación (8) corresponde a un vector de series de tiempo diferenciado. Por último, si 0<r<p existe r vectores de cointegración, en el caso Π=αβ' donde α y β tienen la propiedad de que β’X t es estacionaria, en este caso la ecuación (8) se interpreta como un Modelo de Corrección de Error (MCE). Para testear la hipótesis de r vectores de cointegración o Π=αβ' se emplean los estadísticos de la traza y de autovalores. La prueba estadística de la traza indica en su hipótesis nula la existencia de al menos r vectores de cointegración y se calcula como
donde son p - r autovalores estimados. Por otro lado, la prueba de autovalores para la hipótesis nula de r vectores de cointegración; está dada por
Ambas pruebas sugieren cointegración en presencia o ausencia de componentes determinísticos en el modelo dinámico.
4. Especificación del modelo
La especificación del modelo de la PPP considera dos formatos: el primero es la paridad en su forma absoluta y el segundo en su forma relativa.
4.1 PPP en su forma absoluta
Para el planteamiento de los modelos de la PPP se siguen los resultados de Pérez y Vega (1993), Edison (1987) y Jaramillo y Serván (2012), quienes consideraron incorporar el nivel de precios del sector transable, la producción nacional y la producción extranjera al modelo original de paridad de la ecuación (3). Asimismo, Jaramillo y Serván (2012) consideraron la inclusión de la paridad descubierta de tasas de interés (UIP, por sus siglas en inglés) al modelo de paridad para el caso peruano. El planteamiento de los modelos econométricos de la PPP en su forma absoluta se presenta a continuación
donde αi ,i=1,…,4 son los parámetros, e t es el logaritmo natural del tipo de cambio, p t es el logaritmo natural del nivel de precios doméstico, p * es el logaritmo natural del nivel de precios extranjero, p es el logaritmo natural del nivel de precios transables doméstico, p * es el logaritmo natural del nivel de precios del sector transable extranjero, y t es el logaritmo natural del nivel de producción doméstica, y * es el logaritmo natural del nivel de producción extranjera, i es la tasa de interés doméstica e i * es la tasa de interés extranjera para el período t. El término de error se representa por μ t . A priori se espera que, para el cumplimiento de la PPP en su versión absoluta, los parámetros tomen los valores α 0 =0, α 1 =α 2 =1, que en equivalencia indican la hipótesis nula de eficiencia de mercados en el largo plazo.
4.2 PPP en su forma relativa
Para el planteamiento del modelo econométrico de la PPP en su versión relativa dada por la ecuación (6), se siguen los avances de Pérez y Vega (1993), Edison (1987), Jaramillo y Serván (2012) y Muñoz (2011) quienes consideraron una ampliación con las diferenciales del nivel de precios del sector transable, la producción nacional y la producción extranjera. Asimismo, consideraron incluir al modelo (6) la UIP en variaciones. Los modelos de la PPP en su versión relativa están dados por:
donde β 0 ,β 1 y β 2 son parámetros de los modelos, Δe t es la primera diferencia del logaritmo natural del tipo de cambio, Δpt es la variación del logaritmo natural del índice de precios al consumidor, Δp t * es la variación del logaritmo natural del nivel de precios extranjero, Δp trans,t es la variación del logaritmo natural del nivel de precios del sector transable, Δp * trans,t es la variación del logaritmo natural del nivel de precios del sector transable extranjero, Δy t es la variación del nivel de producción doméstico, Δi t es la variación del logaritmo natural de la tasa de interés y Δi * es la variación de la tasa de interés extranjera en el período t. El término de error se representa por ϵ t para todo el período t. Ahora bien, para el cumplimiento de la PPP a priori se requiere que β 0=0 y β 1=1.
5. Resultados empíricos
En esta sección se muestra el desarrollo de la verificación del cumplimiento de la hipótesis de la PPP en sus formas absoluta y relativa para Perú y Estados Unidos, a partir de las estimaciones econométricas descritas. En este sentido, se emplean las formas funcionales de los modelos 1A-4A, 1R-4R presentadas líneas atrás para las ecuaciones de paridad de largo plazo en sus versiones absoluta y relativa, respectivamente. En la versión absoluta, el primer modelo recoge la relación de los niveles de precios doméstico y extranjero con el tipo de cambio; el segundo modelo reemplaza los niveles de precios de la especificación anterior por los precios de los bienes transables y no transables; el tercer modelo analiza la productividad como un factor adicional a la ecuación de paridad de precios; y el cuarto modelo presenta la unión de los factores de la PPP y la UIP. Para la versión relativa de la PPP, las ecuaciones descritas con anterioridad se expresan por medio del diferencial Δ en todas las determinantes de las formas funcionales. Además, las expresiones en brechas Δx -Δx * hacen referencia a shocks exógenos que afectan directamente la variación Δe t del tipo de cambio. La base de datos empleada para el análisis se obtuvo de la página web del Banco Central de Reserva del Perú (BCRP, 2019) para el caso de las variables domésticas, y del Banco de la Reserva Federal de Estados Unidos (BLS, 2019) para las variables extranjeras. En el análisis y filtrado de la información se consideró lo siguiente: para el tipo de cambio et, se emplea el promedio del período interbancario soles/dólar (S/ por US$); para el nivel de precios doméstico se emplea el Índice de Precios al Consumidor de Lima Metropolitana (2009=100); para el nivel de precios extranjero p * se utiliza el Índice de Precios al Consumidor Urbano de Estados Unidos (índice 1982=100). Para el nivel de precios transable de la economía doméstica p trans,t se hace uso del Índice de Precios al Consumidor transable (índice 2009=100); para el nivel de precios transable extranjero p trans,t se emplea el Índice de Precios al Consumidor de Estados Unidos (índice 1982=100). Para las variables de producción y e y * de las economías doméstica y extranjera, respectivamente, se emplea la información del Producto Bruto Interno (PBI) en millones de soles para el caso peruano y la información de la Producción Bruta de Estados Unidos (GDP, por sus siglas en inglés) en billones de dólares para la economía extranjera. Para el caso de la GDP, la información se transforma en unidades de soles al multiplicarla previamente por el tipo de cambio. Para la especificación de los modelos de UIP se emplea la tasa de interés doméstica i t usando las tasas de interés activas y pasivas promedio de las empresas bancarias en moneda nacional; para la tasa extranjera i * se emplea la tasa de interés efectiva federal de Estados Unidos ambas tasas son convertidas a índices para su análisis.
El paso siguiente en el procesamiento de la información estadística fue transformar todas las variables señaladas en unidades índices y en la moneda de Perú (soles). Luego, se utilizó la transformación logarítmica en base e, llamada también logaritmo neperiano ln x para todas las variables x descritas. El período de análisis al que se hace referencia es el mensual 2000-2019, en el que se consideró un total de 228 observaciones. En la Tabla 1 se muestran las principales estadísticas descriptivas de las variables utilizadas para la estimación. Para esta finalidad se utilizó el software econométrico STATA 14®.
Tabla 1 Estadística descriptiva de las variables económicas 2000-2019
| Lista de variables | Abreviatura | Obs. | Media | Desv. estánd. | Mínimo | Máximo |
| Tipo de cambio nominal (S/ por $) | et | 228 | 3,15 | 0,30 | 2,55 | 3,62 |
| Índice de Precios al Consumidor (IPC) | pt | 228 | 99,80 | 14,86 | 78,75 | 128,10 |
| Índice de Precios al Consumidor de EE.UU | pt* | 228 | 211,14 | 23,26 | 168,80 | 246,82 |
| IPC del sector transable | p trans,t | 228 | 99,92 | 12,73 | 80,70 | 123,80 |
| IPC del sector transable de EE.UU. | p* trans,t | 228 | 211,14 | 23,26 | 168,80 | 246,82 |
| Tasa de interés interbancaria | it | 228 | 4,55 | 2,73 | 1,00 | 16,06 |
| Tasa de interés de EE.UU. | it* | 228 | 1,76 | 2,02 | 0,07 | 6,54 |
| Producto Bruto Interno (PBI en mill. S/) | yt | 228 | 32.706,41 | 14.872,5 | 12.669,05 | 70.956,52 |
| Producción Bruta EEUU (GDP en bill. $) | yt* | 228 | 4.876,99 | 1.056,53 | 3.000,86 | 7.536,10 |
Fuente: elaborado por los autores.
La evolución de las variables económicas y su relación con el tipo de cambio se muestran a continuación. La Figura 1(a) muestra la relación de los niveles de precios nacionales y extranjeros con el tipo de cambio. Se observa que las variables de nivel de precios tienen una relación inversa con el tipo de cambio. La Figura 1(b) muestra la relación existente entre el tipo de cambio y los niveles de precios de los sectores transables para las economías doméstica y extranjera. Esta relación es inversa. La Figura 1(c) muestra el comportamiento del tipo de cambio y las tasas de interés; la Figura 1(d) muestra el comportamiento del nivel de actividad nacional y extranjera con el tipo de cambio.
Para la verificación del orden de integración de las variables de estudio se utilizaron las pruebas de raíz unitaria ADF, propuesta por Dickey y Fuller (1979); la P-P, propuesta por Phillips y Perron (1988), para el análisis sin quiebre estructural; y las pruebas de Zivot y Andrews (1992) y Clemente, Montañés y Reyes (1998) para el análisis con quiebre estructural. La Tabla 2 muestra los resultados de las pruebas calculadas con intercepto/sin tendencia y con intercepto/tendencia. Dada la hipótesis nula de existencia de raíz unitaria de las pruebas, se verifica que, en niveles con intercepto/sin tendencia, las variables tipo de cambio e , nivel de precios doméstico p , precios extranjero p * , precios al consumidor transable p , precios al consumidor extranjero transable p * , tasa de interés doméstica i , tasa de interés extranjera i * , nivel de producción doméstica y y producción extranjera y * tienen una raíz unitaria a un contraste de 1% de nivel de significancia estadística. Similar resultado muestra el cálculo considerando intercepto/tendencia. Por otro lado, al realizar las pruebas de estacionariedad ADF y P-P en primera diferencia, se reporta que todas las series económicas descritas son estacionarias en primera diferencia; de este modo las series en niveles son integradas de orden uno, es decir, son I(1). Estos resultados se muestran en la Tabla 2.
Asimismo, se realiza la prueba de raíz unitaria a las variables económicas considerando los posibles quiebres estructurales. En este sentido, se utilizan las pruebas de raíz unitaria con quiebre de Zivot y Andrews (1992) y la prueba de Clemente et al. (1998) en niveles con intercepto/sin tendencia y en niveles con intercepto/tendencia. Los resultados de la prueba de Zivot-Andrews para el tipo de cambio e t indican la existencia de raíz unitaria con intercepto y tendencia, aunque para el caso del cálculo con intercepto/tendencia indican que la serie no tiene raíz unitaria. Sin embargo, debido a que las series económicas presentan intercepto y tendencia se hace más razonable la consideración de que las series tienen una raíz unitaria o, lo que es lo mismo, no son estacionarias en niveles con intercepto/tendencia. Las demás variables consideradas también aceptan la hipótesis nula de existencia de una raíz unitaria con quiebre estructural para el cálculo con intercepto/ tendencia. La prueba de Clemente-Montañés-Reyes para la verificación de la existencia de raíz unitaria con quiebre muestra que las variables consideradas tienen raíz unitaria con una fecha de quiebre y con resultados muy similares como se muestra en la Tabla 2.
Tabla 2 Prueba de raíz unitaria
| Variable | Prueba de raíz unitaria | Con intercepto y sin tendencia | Con intercepto y tendencia | ||
| Nivel | Primera diferencia | Nivel | Primera diferencia | ||
| et | Dickey-Fuller Aumentada | -1,198 | -9,907** | -0,419 | -9,944** |
| Phillips-Perron | -1,407 | -9,900** | -0,916 | -9,929** | |
| Zivot-Andrews | -4,367++ | -- | -4,157 | -- | |
| Clemente-Montañés-Reyes | -13,241++ | -- | -1,416 | -- | |
| pt | Dickey-Fuller Aumentada | 0,893 | -10,692** | -1,833 | -10,726** |
| Phillips-Perron | 0,669 | -10,562** | -2,069 | -10,580** | |
| Zivot-Andrews | -2,661+ | -- | -3,56 | -- | |
| Clemente-Montañés-Reyes | 22,122++ | -- | 2,323+ | -- | |
| pt* | Dickey-Fuller Aumentada | -1,958 | -8,535** | -1,486 | -8,581** |
| Phillips-Perron | -1,653 | -8,269** | -1,963 | -8,307** | |
| Zivot-Andrews | -4,403++ | -- | -4,634 | -- | |
| Clemente-Montañés-Reyes | 24,833++ | -- | -0,993 | -- | |
| ptrans,t | Dickey-Fuller Aumentada | 0,345 | -8,094** | -1,891 | -8,075** |
| Phillips-Perron | 0,097 | -7,959** | -2,711 | -7,938** | |
| Zivot-Andrews | -3,547++ | -- | -4,111 | -- | |
| Clemente-Montañés-Reyes | 23,052++ | -- | 1,707 | -- | |
| p*trans,t | Dickey-Fuller Aumentada | 0,709 | -12,103** | -2,083 | -12,135** |
| Phillips-Perron | 0,696 | -11,916** | -2,114 | -11,946** | |
| Zivot-Andrews | -4,403++ | -- | -4,634 | -- | |
| Clemente-Montañés-Reyes | 24,821++ | -- | -0,993 | -- | |
| it | Dickey-Fuller Aumentada | -2,978 | -12,079** | -2,762 | -12,050** |
| Phillips-Perron | -3,203 | -12,265** | -3,057 | -12,239** | |
| Zivot-Andrews | -3,529 | -- | -3,265 | -- | |
| Clemente-Montañés-Reyes | -20,101++ | -- | -8,772++ | -- | |
| it* | Dickey-Fuller Aumentada | -1,292 | -9,189** | 0,280 | -9,320** |
| Phillips-Perron | -1,422 | -9,145** | -0,460 | -9,257** | |
| Zivot-Andrews | -3,744++ | -- | -3,852 | -- | |
| Clemente-Montañés-Reyes | -15,792++ | -- | -3,912++ | -- | |
| yt | Dickey-Fuller Aumentada | -2,580 | -24,296** | -16,993 | -24,239** |
| Phillips-Perron | -1,567 | -39,423** | -16,810 | -39,313** | |
| Zivot-Andrews | -4,576+ | -- | -6,306 | -- | |
| Clemente-Montañés-Reyes | 24,633++ | -- | 1,202 | -- | |
| yt* | Dickey-Fuller Aumentada | -6,149 | -25,075** | -21,789 | -25,015** |
| Phillips-Perron | -5,841 | -44,123** | -21,798 | -43,992** | |
| Zivot-Andrews | -5,518++ | -- | -5,412 | -- | |
| Clemente-Montañés-Reyes | 15,321++ | -- | -1,663 | -- | |
Nota: las pruebas ADF y P-P no consideran quiebre estructural y son calculadas con intercepto/sin tendencia y con intercepto/tendencia. Las pruebas de Zivot-Andrews y Clemente-Montañés-Reyes verifican la existencia de raíz unitaria con quiebre estructural. **Indica el rechazo de la hipótesis nula de existencia de raíz unitaria al 1% de significancia. ++Indica el rechazo de la hipótesis nula de existencia de raíz unitaria con quiebre estructural al 1% de significancia. +Indica el rechazo de la hipótesis nula de existencia de raíz unitaria con quiebre estructural al 5% de significancia. Los puntos de quiebre estructural para Zivot-Andrews y Clemente-Montañés-Reyes son seleccionados automáticamente en la prueba.
Fuente: elaborado por los autores.
Para verificar el cumplimiento de la PPP entre Perú y Estados Unidos en sus versiones absoluta y relativa, es necesario la existencia de relaciones de largo plazo entre sus determinantes. Para tal fin, el trabajo utilizó la metodología propuesta por Johansen (1988) y Johansen y Juselius (1990) mediante la estimación de las pruebas de la traza y de autovalores que indican la existencia de ecuaciones de cointegración. La Tabla 3 muestra los resultados de la pruebas de la traza y de autovalores a un valor de 5% de nivel de significancia para las ecuaciones del modelo de la PPP dadas por los Modelos 1A-4A para la versión absoluta de la paridad.
Los resultados indican que los determinantes del modelo de la PPP original definidos con los determinantes de precios domésticos y extranjeros no guardan una relación de cointegración con el tipo de cambio, lo que no permite continuar con el desarrollo del modelo VAR para encontrar el cumplimiento de la hipótesis de paridad. Resultados similares muestran los modelos de paridad con precios transables y el modelo aumentado por la UIP, que no guardan relación de cointegración con el tipo de cambio y, por ende, no cumplen con la hipótesis de paridad para el sol peruano ni para el dólar estadounidense. Por otro lado, el Modelo 3A definido para la paridad con nivel de producción, indica la existencia de una relación de largo plazo entre sus determinantes, lo que hace posible la estimación VAR para el contraste de la hipótesis de paridad en su versión absoluta. En este sentido, se verifica la relación de causalidad de las variables del Modelo 3A usando la prueba de causalidad de Granger (1980, 1988), en la que se reporta que para un valor de significancia del 5%, el nivel de precios doméstico p t , precios extranjeros p * , nivel de producción y y producción extranjera y * causan individualmente en sentido de Granger al tipo de cambio e t , esta causalidad también se cumple de modo conjunto sobre el tipo de cambio a un nivel de significancia del 5%. Por otro lado, la variable et no causa en sentido de Granger las variables enunciadas al 5% de significancia.
Tabla 3: Test de cointegración de Johansen - PPP absoluto
| Hipótesis | Estadístico | 0,05 | Prob.** | Estadístico | 0,05 | Prob.** |
| N° de EC(s) | de la traza | Valor Crítico | autovalores | Valor Crítico | ||
| Modelo 1A (PPP original) | ||||||
| r=0 | 16,943 | 29,797 | 0,644 | 11,227 | 21,132 | 0,625 |
| r≤1 | 5,716 | 15,495 | 0,729 | 4,738 | 14,265 | 0,775 |
| r≤2 | 0,978 | 3,841 | 0,323 | 0,978 | 3,841 | 0,323 |
| Modelo 2A (PPP con precios transables) | ||||||
| r=0 | 9,500 | 29,797 | 0,987 | 6,003 | 21,132 | 0,983 |
| r≤1 | 3,497 | 15,495 | 0,940 | 3,469 | 14,265 | 0,911 |
| r≤2 | 0,028 | 3,841 | 0,867 | 0,028 | 3,841 | 0,867 |
| Modelo 3A (PPP con producción) | ||||||
| r=0* | 83,773 | 69,819 | 0,003 | 4,850 | 33,877 | 0,001 |
| r≤1 | 35,922 | 47,856 | 0,400 | 20,821 | 27,584 | 0,287 |
| r≤2 | 15,101 | 29,797 | 0,774 | 10,011 | 21,132 | 0,744 |
| Modelo 4A (PPP + UIP) | ||||||
| r=0 | 68,039 | 69,819 | 0,069 | 29,715 | 33,877 | 0,145 |
| r≤1 | 38,324 | 47,856 | 0,288 | 22,147 | 27,584 | 0,213 |
| r≤2 | 16,177 | 29,797 | 0,700 | 11,709 | 21,132 | 0,577 |
Indica rechazo de la hipótesis nula a un nivel de 5% de significancia. El número de vectores de cointegración se escribe como r=0 cuando no existe algún vector; r≤1 cuando existe al menos un vector; y r≤2 cuando al menos existen dos vectores. ** Los valores de probabilidad o p-values son usados de las tablas de Mackinnon et al. (1999) para la hipótesis de cointegración.
Tabla 4: Test de cointegración de Johansen - PPP relativo
| Hipótesis | Estadístico | 0,05 | Prob.** | Estadístico | 0,05 | Prob.** |
| N° de EC(s) | de la traza | Valor Crítico | autovalores | Valor Crítico | ||
| Modelo 1 (PPP original) | ||||||
| r=0* | 116,906 | 15,495 | 0,000 | 82,878 | 14,265 | 0,000 |
| r≤1* | 34,028 | 3,841 | 0,000 | 34,028 | 3,841 | 0,556 |
| Modelo 2 (PPP con precios transables) | ||||||
| r=0* | 113,362 | 15,495 | 0,000 | 75,485 | 14,265 | 0,000 |
| r≤1* | 37,878 | 3,841 | 0,000 | 37,878 | 3,841 | 0,000 |
| Modelo 3 (PPP con producción) | ||||||
| r=0* | 188,463 | 29,797 | 0,000 | 108,820 | 21,132 | 0,000 |
| r≤1* | 79,643 | 15,495 | 0,000 | 50,142 | 14,265 | 0,000 |
| r≤2* | 29,501 | 3,841 | 0,000 | 29,501 | 3,841 | 0,000 |
| Modelo 4 (PPP + UIP) | ||||||
| r=0* | 237,259 | 29,797 | 0,000 | 114,433 | 21,132 | 0,000 |
| r≤1* | 122,825 | 15,495 | 0,000 | 78,808 | 14,265 | 0,000 |
| r≤2* | 44,017 | 3,841 | 0,000 | 44,017 | 3,841 | 0,000 |
*Indica rechazo de la hipótesis nula a un nivel de 5% de significancia. El número de vectores de cointegración se escribe como r=0 cuando no existe algún vector; r≤1 cuando existe al menos un vector; y r≤2 cuando al menos existen dos vectores. ** Los valores de probabilidad o p-values son usadas de las tablas de Mackinnon et al. (1999) para la hipótesis de cointegración Fuente: elaborado por los autores.
Al conocer el orden de causalidad, se estimaron los parámetros del modelo de paridad utilizando el Modelo de Corrección de Error (MCE) con cuatro retardos establecidos por los estadísticos de Akaike (AIC) y Schwartz (SBIC). De la estimación del MCE se obtuvo que el coeficiente de corrección de error (λ), que mide la velocidad de ajuste del modelo ante un shock en el equilibrio de largo plazo del vector de cointegración, es estadísticamente significativo y con signo negativo, lo que indica que este sistema se encuentra en equilibrio, pues el parámetro es igual a cero en términos estadísticos. En este sentido, el modelo de largo plazo que representa la ecuación de la PPP en su forma absoluta del modelo 3A con determinantes de nivel de actividad; queda estimada como
donde los signos son los esperados y el nivel de precios doméstico resulta no significativo. Asimismo, sobre los valores de los coeficientes se observa que el coeficiente del nivel de precios doméstico es p t igual a α 1 =0,600 y el coeficiente del nivel de precios extranjero es igual a α 2 =8,102, por lo que resultan ser diferentes (α 1 ≠α 2 ≠1), lo que muestra el rechazo de la PPP en su versión absoluta para el Modelo 3A de la PPP con producción. Para verificar esta hipótesis se utilizó la prueba de Wald y Wolfowitz (1940) mostrado en la Tabla 5.
Tabla 5 Prueba de Wald-Wolfowitz para la hipótesis de la PPP
| Parámetro | Descripción | PPP versión absoluta | Parámetro | Descripción | PPP versión relativa | ||||||
| 1A | 2A | 3A | 4R | 1R | 2R | 3R | 4R | ||||
| α0 | coeficiente | -- | -- | 14,817 | -- | β0 | coeficiente | 0,001 | 0,001 | 0,019 | 0,001 |
| Std. Err. | -- | -- | 1,042 | -- | Std. Err. | 0,369 | 0,365 | 0,228 | 0,247 | ||
| Wald | -- | -- | 14,215 | -- | Wald | 0,004 | 0,003 | 0,086 | 0,007 | ||
| p-value | -- | -- | 0,000 | -- | p-value | 0,498 | 0,498 | 0,465 | 0,496 | ||
| α1 | coeficiente | -- | -- | 0,600 | -- | β1 | coeficiente | 2,577 | 3,931 | 3,045 | 5,024 |
| Std. Err. | -- | -- | 0,473 | -- | Std. Err. | 0,264 | 0,366 | 1,899 | 0,473 | ||
| Wald | -- | -- | 1,268 | -- | Wald | 5,974 | 7,995 | 1,077 | 8,496 | ||
| p-value | -- | -- | 0,103 | -- | p-value | 0,000 | 0,000 | 0,141 | 0,000 | ||
| α2 | coeficiente | -- | -- | 8,102 | -- | ||||||
| Std. Err. | -- | -- | 1,042 | -- | |||||||
| Wald | -- | -- | 6,813 | -- | |||||||
| p-value | -- | -- | 0,000 | -- | |||||||
Notas: con el fin de verificar las hipótesis de α0=0, α1=α2=1 para la versión absoluta y β0=0 y β1=1 para la versión relativa de la PPP se utilizó la prueba de Wald y Wolfowitz (1940).
Fuente: elaborado por los autores.
Para el cumplimiento de la PPP en su versión relativa, dada por los modelos 1R-4R, se verifica inicialmente la existencia de relaciones de largo plazo entre sus determinantes, haciendo uso de la metodología propuesta por Johansen (1988) y Johansen y Juselius (1990) mediante las pruebas de la traza y de autovalores. Los resultados se muestran en la Tabla 4, en la que para un valor del 5% de significancia se reporta la existencia de ecuaciones de cointegración para los modelos de paridad planteados. En consecuencia, el modelo de la PPP en su versión relativa calculada con las variaciones del tipo de cambio y el nivel de precios nacional y extranjero tienen hasta dos ecuaciones de cointegración al igual que el Modelo 2A definido en términos de variaciones del tipo de cambio y los precios transables de Perú y Estados Unidos respectivamente. Asimismo, los modelos de paridad descritos en términos de variación y aumentados por las variaciones del nivel de producción nacional y extranjera muestran la existencia de tres ecuaciones cointegradas al igual que el modelo de paridad aumentada por la UIP en su forma relativa.
Para verificar el cumplimiento de la PPP en su versión relativa del modelo 1R, se verifica el número óptimo de retardos que serán incluidos. Siguiendo los resultados de los estadísticos Akaike (AIC) y Schwartz (SBIC), se obtuvo que tres es el número óptimo de retardos para el modelo. Luego, con base en la estimación del MCE se obtuvo el modelo de largo plazo que representa la ecuación de la PPP en su forma relativa del modelo 1R, dada por
donde Δe t es la primera diferencia del tipo de cambio. Los signos son los esperados, sin embargo los valores de los coeficientes del nivel de precios doméstico que da un valor de 2,577 es diferente de 1, presente en la Tabla 5, lo que lleva a la conclusión del incumplimiento de la forma relativa de la PPP para el caso peruano. Para el Modelo 2R se determina un número óptimo de retardos igual a dos. El modelo de largo plazo obtenido por MCE se encuentra estimada y es el siguiente:
Los signos son los esperados; sin embargo, el valor del coeficiente del nivel de precios doméstico da un valor de β 1=3,931 es diferente de 1, lo que lleva a la conclusión del incumplimiento de la forma relativa de la PPP. De manera similar, el modelo 3R se calcula con tres retardos y, posterior a la estimación del MCE, se encontró el modelo de largo plazo dado por
Los signos son los esperados, sin embargo, el valor del coeficiente del nivel de precios doméstico da un valor de β 1= -3,045 es diferente de 1 (ver Tabla 5), lo que lleva a la conclusión del incumplimiento de la forma relativa de la PPP para el caso peruano.
Finalmente, el modelo 4R se calcula con tres retardos óptimos y el modelo de largo plazo que representa la ecuación de PPP en su forma relativa está dada por,
Los signos son los esperados, sin embargo, el valor del coeficiente del nivel de precios doméstico da un valor de β 1=5,024 diferente de 1 (ver resultados del test de Wald-Wolfowitz en la Tabla 5), lo que lleva a la conclusión del incumplimiento de la forma relativa de la PPP para el caso peruano. El resumen de los resultados de los modelos de la PPP en sus versiones absoluta y relativa se muestran en la Tabla 6, en la que se observa que para la versión absoluta el único modelo que muestra cointegración en sus variables es el modelo 3A de la PPP con producción. Para la forma relativa de la PPP, los cuatro modelos estimados presentan cointegración en sus variables. Por otro lado, no se cumple la hipótesis de la paridad para ningún modelo del tipo de cambio descrito en su forma absoluta y relativa.
Tabla 6 Resumen de los modelos de PPP para Perú y Estados Unidos
| Modelos | ¿Existe cointegración entre sus variables?a | ¿Cumple la PPP?b |
| FORMA ABSOLUTA | ||
| Modelo 1A (PPP original) e =α +α p +α p *+μ | No | No |
| Modelo 2A (PPP con precios transables) e =α +α p +α p *+μ | No | No |
| Modelo 3A (PPP con producción) e =α +α p +α p *+α y +α y *+μ | Si | No |
| Modelo 4A (PPP + UIP) e =α +α p +α p *++α i +α i *+μ | No | No |
| FORMA RELATIVA | ||
| Modelo 1R (PPP original) Δe =β +β (Δp -Δp *)+ϵ | Sí | No |
| Modelo 2R (PPP con precios transables) Δe =β +β (Δp -Δp *)+ϵ | Sí | No |
| Modelo 3R (PPP con producción) Δe =β +β (Δp -Δp * )+β (Δy -Δy * )+ϵ | Sí | No |
| Modelo 4R (PPP + UIP) Δe =β +β (Δp -Δp * )+β (Δi -Δi * )+ϵ | Sí | No |
Notas: los modelos fueron estimados con la metodología VAR. aLa cointegración se hace a partir de los estadísticos de la traza y de autovalores de Johansen para ambas versiones de paridad. bLa hipótesis de paridad para la versión absoluta es α 0 = α 1 = α 2 = 1 y para la versión relativa β 0= 0 y β 1= 1. Fuente: elaborado por los autores con base en los resultados de STATA 14®.
Para evaluar la dinámica del tipo de cambio y para el ajuste de la variable endógena a shocks exógenos, se realiza el análisis de impulso-respuesta al modelo original de la PPP. En esta práctica nos enfocamos en shocks de oferta y demanda de la PPP original. La Figura 2(a) presenta el efecto de un shocks ortogonal de oferta sobre el tipo de cambio e t . Se observa que el tipo de cambio sufre una apreciación abrupta como respuesta al shock, y pasado un tiempo de aproximadamente cinco períodos, el tipo de cambio regresa a su estado estacionario. Por otra parte, una alteración fuerte del nivel de precios extranjero p * ocasiona un desequilibrio en el tipo de cambio que se refleja en una apreciación permanente y un posible nuevo estado estacionario. En este sentido, ante este shock generado por el nivel de precios extranjeros, el BCRP se vería muy motivado para realizar alguna operación de mercado abierto con la finalidad de regresar a su estado estacionario original al tipo de cambio. Por otra parte, un shock de demanda en la producción doméstica de la Figura 3(c) eventualmente trae al tipo de cambio a su equilibrio en al menos cinco períodos, pero termina generándole un desequilibrio permanente y un nuevo equilibrio de estado estacionario. Para el caso de un shock de demanda sobre la actividad extranjera y * , el tipo de cambio sufre una alteración drástica que trae como consecuencia un desequilibrio permanente al tipo de cambio y la adaptación de un posible estado estacionario. Los movimientos de adaptación del tipo de cambio como resultados a shocks de oferta y demanda son razonables, pues el tipo de cambio es una variable económica muy sensible a los shocks exógenos y justamente las políticas monetarias en Perú están orientadas a mantener un equilibrio en un cierto estado estacionario que garantice la planificación en la economía, especialmente en la inversión, ya que el país realiza sus transacciones en moneda extranjera por ser un país parcialmente dolarizado.
Conclusiones
El presente trabajo buscó contrastar la validez de la PPP entre Perú y Estados Unidos para el período 2000-2019. En este sentido, se verifica el cumplimiento de la PPP en sus formas absoluta y relativa para diferentes formas funcionales propuestas en el trabajo, tomando como base las investigaciones más recientes en la ciencia económica que incluyen como determinantes el sector transable, el sector producción y la teoría de la UIP. El análisis de los resultados se hace con base en la metodología de Johansen, para verificar la existencia de relaciones de largo plazo y la aplicación del VAR para hallar las ecuaciones respectivas. A partir de los resultados, se encontró que para los cuatro modelos de la versión absoluta de la PPP el único modelo que muestra cointegración entre sus determinantes es el modelo de la PPP añadido por el sector producción; los otros modelos muestran la inexistencia de ecuaciones de cointegración para sus determinantes. Luego, verificando el cumplimiento de la PPP en su forma absoluta, se encontró que ningún modelo da evidencia del cumplimiento de esta hipótesis ya que sus coeficientes de los niveles de precios nacionales y extranjeros, aunque presentan los signos esperados, son diferentes a la unidad, lo que en efecto lleva a la conclusión del incumplimiento de la hipótesis de equilibrio del mercado en el largo plazo para el caso peruano. Por otro lado, al estimar la PPP en su forma relativa, se encontraron se encontró relaciones de largo plazo para cada una de las formas funcionales; sin embargo, los modelos no cumplen la PPP debido a que los coeficientes del diferencial de precios, diferencial del nivel de actividad y del diferencial de tasas de interés son diferentes de la unidad, lo que lleva a la conclusión del incumplimiento de la forma relativa de la PPP entre Perú y Estados Unidos.
En resumen, el trabajo reporta que no se cumple la hipótesis de la PPP para el sol peruano ni para el dólar estadounidense en ninguna de sus formas funcionales presentadas, lo que da certeza del rechazo de la hipótesis de eficiencia de mercados en el largo plazo para Perú y Estados Unidos. Los trabajos de Jaramillo y Serván (2012) y Muñoz (2011) muestran resultados similares en su investigación para el caso peruano. Por otro lado, es posible que dicha paridad entre Perú y Estados Unidos se cumpla en un horizonte de tiempo más grande. Finalmente, al realizar el análisis de impulso-respuesta de los shocks de oferta y demanda sobre el modelo de paridad, se verifica que el tipo de cambio es muy sensible a los shocks y que solo ante variaciones en los precios domésticos el tipo de cambio es capaz de regresar a su estado estacionario. Para los otros eventuales movimientos ocasionados por los shocks, la autoridad monetaria sería la encargada de regresarla a su estado estacionario inicial mediante políticas en el mercado cambiario y monetario que afectan el tipo de cambio. En caso contrario, el tipo de cambio buscaría un nuevo equilibrio de estado estacionario para contrarrestar el shock sufrido.