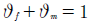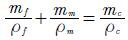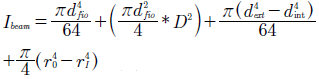1. INTRODUCCIÓN
An attractive characteristic of the so-called shape memory Ni-Ti alloys, among others, is the possibility to change their elasticity modulus (E), by a factor varying from 2 to 3 times, with a moderate increase on the temperature, of approximate 35°C 1-3.
In particular, the cold elasticity modulus of the Ni-Ti wires, according to the literature 2, increases from about EM = 22 GPa, in the martensitic phase to EA = 66 GPa, in the austenite phase, when the temperature increases from 21 to 60°C (EA ≈ 3EM). And, since natural frequencies of structures are affected by stiffness, this inherent feature of Ni-Ti can be explored in vibration control 4, for instance, to avoid a resonance problem 5.
The change in the elasticity modulus, from EM to EA, occurs due to a phase transformation in the alloy, from Martensite (more flexible) to Austenite (stiffer) phase, which is fully completed at about 60°C. This work is concerned with the bending stiffness of hybrid beams, composed of a PP (polypropylene) pipes, endowed with Ni-Ti bars fixed in a groove on their surfaces and fixed by an additional wound external layer of nylon/epoxy. In this work a bar of Ni-Ti was incorporated in the surface of an already finished polypropylene (PP) pipe, which caused a groove in it to spin the bar and generate possible damage in it. The manufacture of the beams can be considered from the manufacture of the pipes incorporating the wire and guarantee the complete spinning and better contact with the matrix, in order to perceive a better response of the increase of the effective bending modulus of the manufactured beams. Experimental and analytical setup on the mechanical behavior of Shape Memory Alloy Hybrid Composite Beams was development as basis on vibration control systems for industrial pipes that carry hot water 5.
2. MATERIALS AND METHODS
The hybrid SMAHC beams were subjected to 3-point bending and tested in two conditions: (i) with the Ni-Ti wires at 25°C; and (ii) at 60°C. In particular, for beams tested in the vertical position, the elasticity modulus increased from 18% to 31%, when the wires were heated to 60°C. Fig. 1, shows the Ni-Ti bar in vertical position.
Since the Ni-Ti bars (Memory-Metalle GmbH) need to be heated up to 60°C, in order to covert 100% of the Ni-Ti martensitic phase into austenite, the specimens were prepared using 500 mm long PP pipes, with external diameter 50 mm and nominal wall thickness 7 mm, used in hot water systems, which can operate in temperatures up to 80°C.
The nominal diameter of the Ni-Ti bars is 6mm and grooves compatible with this diameter were machined in the PP pipes to accommodate the bars, as shown in Fig. 2. One thin layer of the adhesive Araldite F (E = 5.1 GPa), which can withstand up to 80°C in service, was used to fix the Ni-Ti bars. For the experiments, 2 pipes with Ni-Ti bars and filament wound external layers of nylon/epoxy (i.e. SMAHC beams) were manufactured. Two pipes of pure PP, without Ni-Ti and nylon/epoxy, were also tested.
The composite manufacturing process was performed by cleaning the the pipes surface with alcohol and throwing hot air to make it clean and free of grease and dirt. Then the Ni-Ti wire was prepared with the oxide-free surface by the chemical stripping process with the Kroll reagent (91% Vol H2O, 6% Vol HNO3 and 3% Vol HF). Then, 6 grams of epoxy resin (Araldite F / HY 956) was prepared in order to impregnate the pipe groove for the incorporation of the steel or Ni-Ti wire into the pipe, while starting the nylon coil (polyethylene). The winding process begins by strongly gluing the nylon tip to the surface closest to the end of the pipe, so the system is slowly rotated to distribute the nylon over the entire length of the pipe. This procedure lasts approximately one and a half hours for each pipe. Figure 3 shows the manufacturing process. Finally, when the pipe was wound with the nylon, another quantity of epoxy resin, this time 40 grams of resin (32 g araldite F / 8 g HY 956) was prepared considering a ratio of 100 pp of adhesive to 25 pp of hardener, and the expected layer volume of 31 cm3, considering the thickness of the desired layer of t = 1.5 mm taking into account the dimensions of the incorporated system (Ni-Ti).
In circular winding process with nylon, it was necessary to know the volumetric fractions of both fiber and matrix, in order to calculate the effective bending modulus of this layer. In this case, as the nylon is wound 90 degrees with respect to the vertical axis x of the beam, the fibers are mechanically requested in the direction 2, that is, the modulus of elasticity E2, calculated by the rule of the mixtures.
Considering that initially 61 grams of nylon fiber was used in the winding of the composites with steel wire, and only 48 grams of nylon fiber for the composite beams with Ni-Ti wire, the volumetric fractions of the matrix and fiber, respectively. Table 3.10 shows the calculation of the volumetric fractions of the coiled layer of nylon/epoxy coating. In addition, considering that the volumetric fraction of voids can be neglected because it has a very small value in comparison to the values related to fibers and matrices, the volumetric ratio is:
where
 f
and
f
and
 m
are the fiber and matrix volumetric fractions, respectively. Equation 1 can also be written as follows:
m
are the fiber and matrix volumetric fractions, respectively. Equation 1 can also be written as follows:
whereV f is the volume of fibers,V m is the volume of the matrix andV c is the volume of the composite.
by replacing the fiber mass and its density, the mass of the matrix and its density and knowing the mass of the layer, the density can be calculated with equation 3 and hence the volume of the composite and the volumetric fractions of fiber and matrix respectively, as shown in Table I. Likewise, the volumetric fraction of fiber and matrix was calculated for the coiled coating of the composite with Ni-Ti wire, because less amount of nylon fiber was used to try to favor a better impregnation of the epoxy resin in both the tube and in the fiber of nylon.
On the external surface of the pipe, as shown in Fig. 3, a layer of nylon threads in a matrix of epoxy resin (Araldite F) was wound to hold the Ni-Ti tightly.
Using the MTS-810 Universal Machine, at a rate of 1 mm per minute, and a load cell of 1 KN; following the standard test methods (6), four beams were subjected to 3-point bending in the elastic regime at 21°C, two pure PP beams and two SMAHC beams, as shown in Fig. 4. And, besides the tests at 21°C (room temperature), the Ni-Ti wires were also heated up to 56°C, using a heat gun, in order to transform the martensite phase of Ni-Ti into austenite. The diagrams of shear forces, bending moments (M), inclinations presented in Fig. 5.
In the tree point test presented in Figs. 4, the maximum displacement (( max, deflection at the middle point) of the beams, which is related with the static applied force (P), is given by eq. (4):
During the tests carried out in the MTS-810 machine MTS-810,( max as well as P were measured. Thus, knowing the span, L = 467 mm, and the moment of inertia I of the cross section of the beam, the experimental elasticity bending modulus of the beam can be obtained using eq. (4). For the pure PP pipe itself, Inertia I, is given by eq. (5), where di = dint and de = dext was calculated from radius in Fig. 6.
The elasticity flexural modulus of the SMAHC beams, ExF, can also be obtained analytically, using a procedure described in 6,7,8 by means of eq. (6).
where: Iyy is the global moment of inertia of the cross section shown in Fig. 5; Ex k is elasticity modulus of a single layer, and Iyy k is the moment of inertia of a simple layer. Iyy = Ibeam is given by eq. (7)
where: dfio is the diameter of the Ni-Ti bar; D is the distance from the global centroid to the Ni-Ti bar centroid; r0 is the external radius of the nylon/epoxy layer; and rI is its internal radius. The elasticity modulus of the nylon/epoxy layer, calculated using micromechanics approach (1/E2 = vf/Ef + vm/Em) 8, is 1700 MPa. The volume fractions are vf = 55% of nylon and vm = 45% of epoxy, Ef = 1 GPa and Em = 5.1 GPa.
In addition to the configuration presented in Fig. 1, where the Ni-Ti bar is at 0° from axis y, the SMAHC beams where also tested with the Ni-Ti bars at 90° and 180°, as shown in Fig. 6.
3. EXPERIMENTAL AND THEORETICAL RESULTS
Samples of the Ni-Ti bars, protected by an inert atmosphere of nitrogen, were tested in a Netzsch DSC 200 F3 Differential Scanning Calorimeter. The transformation temperatures Ms (Martensite Start), Mf (Martensite Finish), As (Austenite Start), and Af (Austenite Finish) are presented at Table II.
On the other hand, scanning electron microscopy with energy dispersive spectroscopy (EDS) analysis (JEOL model JSM 7001F) (Fig. 7) were used on the Ni-Ti Bar surface. This test shows that it consists of Ti and Ni elements at the largest area. The atomic weights (at.%) of Ti and Ni elements are very close to the nominal compositions of Nitinol in spite of minor variations by different manufacturers 9. Results of atomic and weigh percentages are shown in table III.
On the other hand, XRD analysis, shown in fig 8, were recorded in the Bruker AXS D-8 Advance XRD machine in the 2θ range of 10° to 100° with scan speed of 1°/min, and increments of 0.05°, CuKα = 1,5418 Å. The peak of the |110| Cubic reflection gives an idea of the austenitic phase transformation in Ni-Ti alloy, cubic phase (ICDD, PDF 65-7711) 11. Eight peaks (M1 to M8) were associated with X-ray reflection peaks corresponding to martensitic phase at room temperature, monoclinic phase (ICDD, PDF 27-344). It shows a crystallographic distortion in NiTiNol transition 11.
First, from the three point bending tests in the MTS-810 machine, the force, P, as well as the deflection at the middle section (x = L/2) of the beams,( max, were recorded and plotted. The SMAHC beams were tested in three configurations (see Fig. 6). Typical P versus( max curve for a PP beam12, is shown in Fig. 7. Using equation (1) their experimental bending modulus were obtained. And, from equations (2) to (4), the respective analytical flexural modulus, ExF, were calculated. Two SMAHC and two PP beams were tested.
The average bending modulus of the PP beams was 757 MPa. All the three-point bending tests were carried out in the elastic regime, with the maximum applied deflections,( max, limited to about 1% of the span (L = 467mm). Following the same test, the average results from SMAHC at room temperature (21°C) are presented in Table IV. These results indicate, as expected, that the contribution of the Ni-Ti bars in the bending stiffness is significantly higher for the 0° and 180°configuration, in comparison with the 90° configuration (see Fig. 6).
Table IV. AVERAGE VALUES OF EFFECTIVE BENDING MODULUS (MPA) AT NI-TI MARTENSITE STATE (21°C)
Source: The authors.
The average results at 56° C are presented in Table V.
Table V. AVERAGE VALUES OF EFFECTIVE BENDING MODULUS (MPA) AT NI-TI AUSTENITE STATE (56°C)
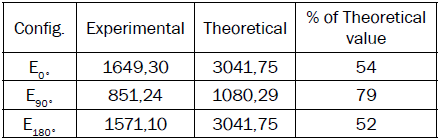
Source: The authors.
The results of Table V also confirm that the Ni-Ti bars are more effective to increase the bending stiffness when they are in the 0° and 180° configurations.
4. DISCUSSION
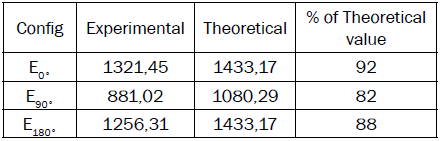
The experimental results showed that the incorporation of Ni-Ti bars in the PP pipes, hold by an external layer of nylon/epoxy, in average, at 21°C, increased the bending stiffness of the PP beam by 92%. And, these experimental results at 21°C were very close to the theoretical predictions, in the range from 88% to 92%, as presented in Table 4. Literature has shown that, in bending 11, Ni-Ti martensite deformation results from the migration of variant interfaces, while in compression the deformation mechanism is mainly due to the generation and movement of lattice defects. These mechanisms are clearly seen in the average values of effective bending elasticity modulus, table 2. Interestingly, the results are quite similar below approximately 100 MPa; however, above this stress the curves diverge rapidly. When the SMAHC material is loaded in pure bending, limited portions of the beam reach stress levels required to detwin the martensite. Close to the neutral axis, in bending, both tension and compression, the beam material remains elastic. Shape memory is dependent on internal stresses and dislocation structures, the elastic material will likely not experience increase of elasticity modulus value during training.
On the other hand, the transformation of from martensite to austenite and vice versa of Ni-Ti Bar of SMACH beam, will also vary spatially through the configurations of the beam due to the relationship between stress and transformation temperature. The result of this variation will be a larger difference between the apparent transformation start and finish temperatures. The effective bending elasticity modulus variation through the thickness of SMACH beams will also affect the vibration control phenomena. The SMAHC beams austenitic transformation induced by temperature was explored when temperature of the Ni-Ti bars increased from T = 21°C (Ni-Ti in the martensite phase) to 56°C (Ni-Ti in the austenite phase) the bending stiffness increased about 25%.
The correlation of the experimental results shown in table 3, with the theoretical predictions, at 56°C, in the range from 52% to 54%, were not as good as those at 21°C, in the range from 88% to 92%, table 4. This suggests that bending modulus of the PP, figure 9, probably decreased with elevation of temperature (from 881,02 MPa in table 4 to 851,24 MPa, shows in table 5, for E90°), and this was not taken into account in the analytical model for 3EM. In fact, in these experiments, the Ni-Ti bars were in the longitudinal direction of the PP pipes. Both, the applied loads and the Ni-Ti bars belong to the symmetry vertical plane of the beam and supports the PP pipe common bending behavior, leading to bigger mechanical strokes within the transformation temperature range.
One of the most important parameters in the research on composites is the manufacturing methods, so important aspects such as the repeatability of composite characteristics are guaranteed 13), (14. With regard to the manual winding device, the manufacturing time and the geometric arrangement of the fibers to be wound in the process are the major drawbacks. The technique can be improved with a system that adjusts with constant movement as a function of the amount of fiber used for winding 13), (14. A motor with speed control next to the device can be thought of, however, any error in the speed control inserts vibration in the distribution of the fiber which can affect the repeatability of the process.
CONCLUSIONS
A cylindrical composite beam manufacturing methodology was developed using a manual winding device designed to adequately handle hybrid beams to be wound with nylon (polyethylene) and impregnated with epoxy resin. The 90° circumferential winding process was successfully done, distributing the nylon fiber (polyethylene) and impregnating with resin homogeneously through the entire length of the beams.
Polypropylene pipes were mechanically tested in the elastic regime to evaluate the elastic modulus in flexion in a three-point test device designed according to ASTM D790-07 applying a force at a speed of 1 mm/min up to the maximum deflection of 5 mm (1% of span).It has been theoretically and experimentally verified in three-point bending tests that the orientation of the steel wire or Ni-Ti, in relation to the plane of application of the load, has a strong influence on the mechanical properties of the composite beam used, that is , for 90° orientation there is no significant contribution of the mechanical properties of the thread to the value of the effective modulus of elasticity; however, for the 0° and 180° orientations, the contributions are much higher by a factor close to 1.5 times.
The bending modulus of composite cylindrical beams with Ni-Ti bar, showed increases of 18% to 31% that are associated to the effects of the phase change of Ni-Ti wire, from martensite to austenite, induced under conditions of temperature increase in the composite, from 21°C to 56°C. This effect gave the composite the adaptive character and can be used in environments where it is required and under two preferential orientations of 0° and 180° degrees with respect to the axis of application of the load 14.
These last results indicate that the SMAHC beams can work as an adaptive structure using the shape memory effect and high damping capability of NITINOL and the future research on viscoelastic behavior, as reported in 15), (16, is necessary for a clear understanding of basic features and trends of a vibration control systems for industrial processes, new materials and applications. Viscoelasticity and phase-transformation effects on the resulting dynamic responses are more pronounced in these materials 17 and are used for the developing damping materials with increased damping capacity over a wide band 18.