1. Introducción
La identificación y pronóstico de las variables asociadas a los mercados eléctricos, son tópicos de gran relevancia para la academia, así como para el sector real, incluyendo gobiernos (y entes reguladores), empresas proveedoras de servicios de energía y consumidores. En particular, el pronóstico de la demanda de energía es un asunto relevante para el contexto actual pues se relaciona con factores medioambientales y económicos (Islam et al., 2020). Desde la perspectiva gubernamental, los reguladores propenden por identificar las tendencias de la demanda para favorecer la gestión de los sistemas eléctricos, ahorrar recursos y proveer estabilidad en los mercados (Mohandes, 2002; Rueda, Velásquez and Franco, 2011). Adicionalmente, los gobernadores se interesan en las proyecciones de demanda ya que se ha mostrado que el consumo de energía va ligado al desarrollo económico y social de algunos países (Barreto and Campo, 2012). Por su parte, a las empresas les interesa contar con modelos de pronóstico que contribuyan a la toma de decisiones para la planeación del suministro eléctrico (Wang et al., 2012; Yang et al., 2016; Jiménez, Donado and Quintero, 2017). Finalmente, a los usuarios, bajo una perspectiva de racionalidad, les interesaría proyectar su consumo para generar estrategias que les permitan mejorar sus flujos de efectivo (Wang et al., 2012; Kubli, Loock and Wüstenhagen, 2018).
Desde la perspectiva de la demanda de energía, los sectores de consumo no residenciales se caracterizan por ser los de mayor participación en la demanda nacional de energía eléctrica en múltiples países (EEA, 2017; IEA, 2017). En el caso colombiano, en particular, los sectores diferentes al residencial representan aproximadamente el 60% del total de la demanda (SUI, 2016); en especial, el sector de explotación de minas y canteras, además de ser un sector estratégico en cuanto a políticas para favorecer la descarbonización de los mercados, es el responsable de más del 21% de la demanda eléctrica de los sectores no residenciales en Colombia (cálculos de los autores usando información de XM (2018)). Adicionalmente, este sector es clave para la economía colombiana, ya que se considera un sector estratégico para el desarrollo nacional pues fomenta la inversión local y extranjera en el país (Pérez Osorno and Betancur Vargas, 2017).
Por tanto, este trabajo se concentra en el análisis de la demanda de energía eléctrica de sectores no residenciales en Colombia, con énfasis en el sector de explotación de minas y canteras, a través del uso de modelos matemáticos con la metodología de series de tiempo, con fines de pronóstico, de forma tal que contribuya como insumo para la toma de decisiones estratégicas para el sector eléctrico en Colombia.
Este trabajo se organiza como sigue: la sección 2 presenta una revisión de la literatura sobre los modelos que se han desarrollado previamente para el pronóstico de demanda eléctrica y sus principales resultados, la sección 3 presenta la construcción y validación de tres modelos bajo la metodología de series temporales para la serie de demanda eléctrica del sector de minas y canteras en Colombia, la sección 4 provee información sobre el desempeño de cada uno de los modelos ajustados y validados, así como una discusión sobre los hallazgos del estudio; y finalmente, la sección 5 presenta las principales conclusiones de este trabajo.
2. Estudios previos sobre pronóstico de demanda eléctrica
Considerando la relevancia del pronóstico de la demanda eléctrica, en la literatura se encuentran múltiples trabajos que abordan este asunto bajo diversas metodologías. En esta sección se revisan algunos de estos estudios y sus principales hallazgos.
Investigaciones previas enfocadas en el pronóstico de demanda en los mercados de energía han utilizado modelos que incluyen redes neuronales, series temporales e inteligencia artificial como se presenta en la Tabla 1 (Shyh-Jier Huang and Kuang-Rong Shih, 2003; Azadeh, Ghaderi and Sohrabkhani, 2008; Franco, Velásquez and Olaya, 2008; Velásquez, Franco and García, 2009; Romero, Hernandez and Lopez, 2011; Rueda, Velásquez and Franco, 2011; Gil, 2016; Nunes Da Silva and Carli Moreira De Andrade, 2016; Jiménez, Donado and Quintero, 2017); cuyos objetivos más destacables abarcan la formulación de modelos matemáticos - estadísticos que describen el comportamiento de una serie de datos y permiten realizar pronósticos con un bajo nivel de error (Deb et al., 2017; Jiménez, Donado and Quintero, 2017). Estos niveles de error en el pronóstico suelen ser comparados utilizando criterios como el Error Absoluto Medio (MAE), como en Rahman & Ahmar (2017), el Error Absoluto Medio Porcentual (MAPE), por ejemplo en Jiménez et al. (2017); Nunes Da Silva & Carli Moreira De Andrade (2016), y la Raíz del Error Cuadrático Medio (RMSE), como en Percy, Aldeen, & Berry (2018); Rocha, Silvestre, Celeste, Coura, & Rigo (2018). Es importante resaltar que obtener modelos de pronóstico con bajos niveles de error en las variables asociadas al mercado eléctrico es un asunto de gran importancia, ya que los errores de pronóstico en este mercado conducen a problemas de balance en el sistema, y consecuentemente a incrementos en los precios de la electricidad Goodarzi, Perera, & Bunn (2019).
Tabla 1 Estudios de pronóstico de demanda de electricidad y sus resultados. Fuente: Elaboración Propia utilizando las referencias citadas
| Referencia | Variable estudiada | Modelo | Desempeño | ||
|---|---|---|---|---|---|
| MAE | MAPE | MSE | |||
| (Azadeh, Ghaderi and Sohrabkhani, 2008) | Demanda eléctrica mensual - Irán | Red Neuronal | 0,260 | 0,018 | 0,120 |
| Serie de Tiempo - ARIMA | 0,69 | 0,042 | 0,750 | ||
| (Franco, Velásquez and Olaya, 2008) | Demanda eléctrica mensual - Colombia | modelo de componentes no observables | 0,030 | 0,250 | |
| (Nunes Da Silva and Carli Moreira De Andrade, 2016) | Demanda eléctrica diaria -curva de carga | ANFIS | 1,890 | ||
| (Gil, 2016) | Demanda eléctrica mensual - Colombia | Modelo aditivo de componentes | 33,705 (GWh) | 0,915 | 1.136,033 (GWh2) |
| (Garzón Medina and Marulanda García, 2017) | Demanda eléctrica corto y mediano plazo -Sector residencial Colombia | Regresión multivariada corto plazo | 4,130 | ||
| Regresión multivariada largo plazo | 54,940 | ||||
| Serie de Tiempo corto plazo | 0,870 | ||||
| Serie de Tiempo largo plazo | 10,370 | ||||
| (Jiménez, Donado and Quintero, 2017) | Demanda eléctrica diaria -región Caribe Colombia | Redes Neuronales | 1,900 | ||
| (Rahman and Ahmar, 2017) | Demanda eléctrica -Estados Unidos | ARIMA | 723502,200 | ||
| Holt Winters Aditivo | 258350,100 | ||||
| Holt Winters multiplicativo | 262260,400 | ||||
| (Gulay, 2019) | Generación eléctrica - Sur África | SARIMA | 1,085 | RMSE: 1,188 | |
| Holt Winters Aditivo | 0,807 | RMSE: 0,888 | |||
| Holt Winters Multiplicativo | 0,727 | RMSE: 0,813 | |||
| Red Neuronal basada en Holt Winters Aditivo | 0,493 | RMSE: 0,629 | |||
| Red Neuronal basada en Holt Winters Multiplicativo | 0,460 | RMSE: 0,543 | |||
| (Jimenez et al., 2019) | Demanda eléctrica mensual - región Caribe, Colombia | Red Neuronal | 3,100 | ||
| Red Neuronal Climática | 1,800 | ||||
Autores como Romero et al. (2011) pronostican la demanda máxima de electricidad para una subestación mexicana usando redes neuronales y modelos ARIMA. Los datos corresponden a información mensual de enero de 1994 a diciembre de 2006, y su pronóstico se realiza con un conjunto de prueba de 6 datos desde junio hasta diciembre de 2006. Los autores encuentran que la red neuronal, en su caso, brindó un menor error de pronóstico.
Por otro lado, en Rahman & Ahmar (2017), se comparan los pronósticos obtenidos para la serie de consumo de energía primaria de Estados Unidos, desde 1973 a 2016, a partir de un modelo SARIMA con respecto a los pronósticos usando Holt Winters aditivo y Holt Winters multiplicativo. En este trabajo se encuentra que, para esta serie, el modelo de Holt Winters aditivo provee el menor error de pronóstico.
Por su parte, Gulay (2019) propone un modelo híbrido entre modelos simples (tipo ARIMA o Holt Winters) con modelos más complejos para el pronóstico de series de tiempo (como redes neuronales artificiales y sistema de inferencia neuro-difuso adaptativo - ANFIS) para capturar tanto la parte lineal como no lineal de los datos de la producción total de energía eléctrica en Suráfrica. En su trabajo encuentra que el mejor modelo simple para los datos fue un Holt Winters multiplicativo, y el mejor modelo complejo híbrido es aquel que usa redes neuronales artificiales basado en un modelo Holt Winters multiplicativo.
Modelos aplicados al caso de Colombia, incluyen a Franco et al. (2008) donde, utilizando los datos mensuales de demanda total del sistema entre agosto de 1995 y enero de 2007, se determinan los componentes no observables de la serie incluyendo tendencia, estacionalidad y error, con el propósito de caracterizar la demanda eléctrica. También se encuentra el trabajo de Velásquez et al. (2009), donde se compara el desempeño del pronóstico de un modelo ARIMA, un perceptrón multicapa y una red neuronal, para la demanda eléctrica agregada colombiana, encontrando mejores resultados en la red neuronal. Trabajos más recientes incluyen el de Gil (2016), quien utilizando un modelo aditivo de series de tiempo, pronostica la demanda eléctrica nacional agregada de Colombia para los períodos 2008 - 2014, encontrando un MAPE de 0,920%. Además se encuentra el trabajo de Garzón Medina & Marulanda García (2017), dónde se proponen proponen modelos de componentes series de tiempo (aditivo y multiplicativo) y modelos de regresión (incluyendo variables como producto interno bruto) para estimar la demanda para el consumo de energía eléctrica en el sector residencial colombiano en el corto y el largo plazo, obteniendo errores que varían entre el 0,870% y el 55%. Y, finalmente, se resalta la investigación de Jimenez et al. (2019), quien utiliza redes neuronales para pronosticar la demanda eléctrica mensual de la región Caribe Colombiana, encontrando un modelo con un MAPE del 1,800%.
A pesar de la existencia de múltiples aproximaciones estadísticas al pronóstico de la demanda de energía, se identifica que hay carencia de modelos de pronóstico con datos recientes para la demanda eléctrica colombiana; y que, además, los trabajos existentes para pronóstico, en el caso colombiano, se enfocan principalmente en el pronóstico del comportamiento agregado de la demanda o en el sector residencial, dejando de lado el estudio de los sectores no residenciales.
Por lo anterior, en este trabajo se estima la demanda eléctrica para el sector no residencial de minas y canteras en Colombia utilizando los criterios MAE, MAPE y RMSE, a partir de modelos estadísticos de series temporales.
3. Materiales y métodos: análisis de la serie temporal
Para el análisis de la demanda comercial de energía eléctrica del sector económico de explotación de minas y canteras, se tomaron 102 registros mensuales disponibles en el portal XM (XM, 2018), correspondientes a los meses de enero de 2010 hasta junio de 2018. Esta variable tiene como unidad de medida kWh.
La figura 1 presenta la gráfica de la serie de tiempo y su descomposición de acuerdo con un modelo de componentes que incluye tendencia, estacionalidad y error. En la figura 1 se observa que la serie pareciera tener una tendencia global creciente y un patrón estacional; por lo tanto, se decide incluir en el análisis modelos aditivos que incluyan tanto los componentes de tendencia como la componente estacional; modelos tipo SARIMA que son análogos a los modelos aditivos de componentes, y finalmente el modelo Holt Winters considerando que es posible que mediante suavizado se puedan obtener buenos resultados de pronóstico.

Fuente: Elaboración propia utilizando (R Core Team, 2017).
Figura 1 Descomposición de la serie de tiempo de demanda comercial de energía eléctrica del sector colombiano de minas y canteras.
Para el ajuste y selección de los modelos de pronóstico se dividió la serie en dos conjuntos de datos, con el objetivo de utilizar un conjunto para el entrenamiento (ajuste) y otro para verificar el pronóstico, tomando de los 102 datos disponibles 90 datos para el entrenamiento, y los últimos 12 para la prueba del pronóstico. Para cada modelo se buscó aquel que presentara los mejores indicadores de ajuste y cuyos errores fuesen ruido blanco. A continuación, se presentan los modelos ajustados, sus indicadores, y las pruebas de validación de los errores para cada uno.
A. Modelo 1 - modelo aditivo de componentes
Se selecciona un modelo que incluye las componentes de tendencia (7£), estacionali-dad(St) y error (£t), y que asume que la serie puede escribirse como la suma de las tres componentes. Las ecuaciones (1) y (2) presenta la forma de este modelo.
En el modelo 1 de componentes (ecuación (1)) se considera que la serie posee una tendencia global que sigue un proceso lineal; y que además la serie posee un componente periódico cuyo patrón estacional se repite cada doce meses. Como indicadores de bondad de ajuste el modelo estructural 1 presentó un R2 de 0,745, un R 2 de 0,705, un AIC de 835,429 y un BIC de 870,426.
Para garantizar la idoneidad del modelo se analizaron sus residuos, buscando que cumplieran los supuestos de normalidad, homocedasticidad e incorrelación. Los errores del modelo estructural no resultaron ser ruido blanco pues incumplían el supuesto de incorrelación, por lo tanto, se ajustó un proceso autorregresivo de orden dos para ésta componente (ver ecuación (2)).
Los parámetros del modelo lineal estacional ajustado se presentan en la Tabla 2.
Tabla 2 Parámetros ajustados, valor p y resultados de la prueba de significancia.
| Parámetro | ESTIMADOR PUNTUAL (PARÁMETRO AJUSTADO) | Valor p* |
|---|---|---|
| 𝛽0 | 300,368 | <2e-16 |
| 𝛽1 | 1,349 | <2e-16 |
| 𝛿1 -enero | 3,634 | 0,763 |
| 𝛿2 - febrero | -29,869 | 0,015 |
| 𝛿3-marzo | -11,608 | 0,337 |
| 𝛿4-abril | -28,018 | 0,022 |
| 𝛿5-mayo | -2,655 | 0,826 |
| 𝛿6-junio | -23,663 | 0,053 |
| 𝛿7-julio | -17,492 | 0,163 |
| 𝛿8-agosto | -8,385 | 0,501 |
| 𝛿9-septiembre | -8,165 | 0,513 |
| 𝛿10-octubre | -3,679 | 0,768 |
| 𝛿11-noviembre | -10,529 | 0,399 |
*Los valores resaltados corresponden a los parámetros estadísticamente significativos a un nivel de confianza del 95%.
Fuente: Elaboración propia utilizando (R Core Team, 2017).
Para verificar la utilidad del modelo se realizaron pruebas de hipótesis de significancia del modelo y sus parámetros. La prueba de significancia del modelo estructural con componentes lineal y estacionalidad modelada con variables indicadoras se presenta a continuación:
Hipótesis: H0 = Ningún parámetro es significativo
vs Hα = Algún parámetro es significativo
Estadístico de Prueba: F = 18,69 ~ F12.77; Criterio de rechazo: Vp < 5%
Como el valor p de esta prueba es 2,2e-16, menor que el nivel de significancia del 5%, se rechaza la hipótesis nula y se concluye que existe al menos un parámetro que explica el comportamiento de los datos. Para identificar los parámetros significativos se realizan pruebas independientes sobre cada parámetro, el valor p para cada parámetro se presenta en la Tabla 2.
Hipótesis: H 0 = El parámetro no es significativo
vs Hα = El parámetro es significativo
Criterio de rechazo: Vp < 5%
En conclusión, de acuerdo con el criterio de rechazo y la información de la Tabla 2, el intercepto (𝛽0), el parámetro 𝛽1 de tendencia lineal, y los parámetros estacionales para los meses de febrero (𝛿 2-febrero ) y abril (𝛿 4-abril ) son significativos a un nivel de confianza del 95% para explicar el comportamiento de la serie de tiempo del consumo eléctrico mensual del sector colombiano de explotación de minas y canteras.
El modelo autorregresivo de orden dos con que se modeló la componente del error (ℇt) para el modelo 1 (ecuación (2)) fue identificado utilizando la función auto.arima y ajustado con la función arima de la librería timsac del software R (R Core Team, 2017); el correspondiente valor de los coeficientes ajustados es φ1 = 0,361 , φ2= 0,212; y la media μ = - 0,593. Los residuales del modelo AR(2) (αt) resultaron ser ruido blanco y las gráficas de validación de los supuestos sobre dichos residuales se presentan en las figuras 2, 3 y 4.
La figura 2 presenta un gráfico de los residuos del modelo para cada observación del conjunto de entrenamiento; con dicha información es posible identificar que no existen patrones que indiquen heterocedasticidad; por tanto, se puede afirmar que gráficamente se cumple el supuesto de varianza constante.

Fuente: Elaboración propia utilizando (R Core Team, 2017).
Figura 2 Gráfico de residuales (αt) del modelo 1 - modelo de componentes.
Respecto al supuesto de incorrelación, se realiza la prueba de hipótesis Ljung-Box y se analiza la gráfica de autocorrelación (fac) que se presenta en la figura 3. La prueba de hipótesis se formula así:
Hipótesis: H0 = αt son incorrelacionados vs Hα= αt son correlacionados
Criterio de rechazo: Vp < 5%
El valor p de la prueba Ljung-Box de correlación para 24 rezagos es de 0,230, por tanto, no se rechaza la hipótesis nula y se concluye que los errores del modelo 1 no presentan correlación. En la figura 3 se observa cómo, consistentemente con los resultados de la prueba, la mayoría de los puntos se encuentran dentro de las bandas de Barlett en la función de autocorrelación de los residuales.

Fuente: Elaboración propia utilizando (R Core Team, 2017).
Figura 3 FAC para los residuales (at) del modelo 1 - modelo de componentes.
Para verificar el supuesto de normalidad se plantea la prueba Shapiro - Wilk.
Hipótesis: H0 = αt distribuye normal vs Hα = αt no distribuye normal
Criterio de rechazo: Vp < 5%
El valor p de la prueba Shapiro-Wilk de normalidad es de 0,146, por tanto, no se rechaza la hipótesis nula y se concluye que los errores del modelo 1 tienen una distribución normal. En la figura 4 se observa cómo, consistentemente con los resultados de la prueba, los puntos en su mayoría se ajustan apropiadamente a la recta, con excepción en algunos puntos de las colas.

Fuente: Elaboración propia utilizando (R Core Team, 2017)
Figura 4 Gráfico Q-Q para los residuales (at) del modelo 1 - modelo de componentes.
Con los resultados anteriores, se verifica entonces el cumplimiento de los supuestos de varianza constante, normalidad e incorrelación para los errores at del modelo 1; por lo tanto, se considera que los residuales αt son ruido blanco y el modelo 1 puede utilizarse para pronosticar.
B. Modelo 2 - modelo SARIMA
Los modelos autoregresivos integrados de media móvil o ARIMA propuestos por Box y Jenkins (Box and Jenkins, 1976) pueden generalizarse para incluir patrones estacionales; en tal caso se habla de los modelos SARIMA (del inglés: seasonal auto-regressive integrated moving average) o ARIMA estacionales, que además de representar matemáticamente la dependencia de los valores de la serie con respecto a las observaciones y errores consecutivos de la serie, también contiene las componentes que representan la dependencia con observaciones y errores separadas por periodos estacionales.
La estructura general de un modelo SARIMA (p,d,q)(P,D,Q)(s), puede escribirse como:
La identificación de los parámetros del modelo (𝜑1 ..., 𝜑𝑝, 𝜙1 ... 𝜙𝑃, 𝜃1 ... 𝜃𝑞,𝜗1 ... 𝜗𝑄) se hace considerando las funciones de autocorrelación (fac) y de autocorrelación parcial (facp), y los criterios de información de Akaike (AIC) y Bayesiano (BIC). Además, se verifica la significancia de los parámetros y el cumplimiento de los supuestos sobre los errores.
Para el caso del consumo de energía eléctrica del sector de explotación de minas y canteras de Colombia se encontró un modelo SARIMA(0,1,1)(0,1,1)(12) es decir, un modelo con una diferencia de orden uno para quitar tendencia, una diferencia estacional de orden 12 para dar cuenta de la estacionalidad y con componentes de media móvil de orden uno tanto para la parte estacional y la no estacional. Los parámetros estimados de este modelo se presentan en la Tabla 3, junto con su respectivo valor p. Los criterios de Akaike (AIC) y el criterio de Información Bayesiana (BIC) correspondientes fueron 7,159 y 6,215 respectivamente.
Tabla 3 Parámetros ajustados y valor p del modelo 2 - SARIMA.
| Parámetro | ESTIMADOR PUNTUAL (PARÁMETRO AJUSTADO) | Error estándar del estimador | Valor p* |
|---|---|---|---|
| ma1 (𝜃1) | -0,596 | 0,094 | 0,000 |
| sma1 (𝜗1) | -0,937 | 0,548 | 0,092 |
*Los valores resaltados corresponden a los parámetros estadísticamente significativos a un nivel de confianza del 95%.
Fuente: Elaboración propia utilizando el paquete "astsa" (Stoffer, 2012; R Core Team, 2017).
Para verificar la utilidad del modelo se realizaron pruebas de hipótesis de significancia sobre sus parámetros. La prueba de significancia de los parámetros 𝜃1 y 𝜗1 del modelo 2 - SARIMA se presenta a continuación:
Hipótesis: H0 =El parámetro no es significativo
vs Hα=El parámetro es significativo
Criterio de rechazo: Vp < 5%
En conclusión, de acuerdo con la hipótesis y la información de la Tabla 3, el parámetro ma1 (𝜃1) es significativo para explicar el comportamiento de los datos con un nivel de confianza del 95%. Por otro lado, el parámetro sma1 (𝜗1) no es significativo al 95% de confianza, pero sí lo es con un nivel de confianza del 90%.
Los supuestos sobre los errores del modelo se validan utilizando información gráfica y pruebas de hipótesis. En la figura 5, se observa que los residuos estandarizados no tienen ningún patrón de heterocedasticidad ni patrones que indiquen no linealidades, por lo que se valida el supuesto de varianza constante.

Fuente: Elaboración propia utilizando (R Core Team, 2017).
Figura 5 Gráfico de residuales (et) del modelo 2 - SARIMA.
En la figura 6 se observa la función de autocorrelación de los residuales, donde puede verse que no hay rezagos en los que haya autocorrelación, estando la mayor parte de ellos dentro de las bandas de Barlett. A continuación, se presenta la prueba formal de incorrelación de Ljung-Box:
Hipótesis: H0 = εt son incorrelacionados vs Hα = εt son correlacionados
Criterio de rechazo: Vp < 5%
La prueba Ljung-Box de correlación arrojó un valor p de 0,645 considerando 24 rezagos, por tanto, no se rechaza la hipótesis nula y se concluye que los errores del modelo SARIMA no presentan correlación.

Fuente: Elaboración propia utilizando (R Core Team, 2017)
Figura 6 FAC para los residuales (st) del modelo 2 - SARIMA.
Finalmente, en la figura 7, se observa un gráfico de probabilidad normal para los residuos, en los que se identifica que una distribución normal es posible. Este supuesto se verifica con la prueba Shapiro Wilk.

Fuente: Elaboración propia utilizando (R Core Team, 2017)
Figura 7 Gráfico Q-Q para los residuales (st) del modelo 2 - SARIMA.
Hipótesis: H0n=nεt distribuye normal vs Hα = εt no distribuye normal
Criterio de rechazo: Vp < 5%
El valor p de la prueba es 0,071, mayor que 0,05, por tanto, no se rechaza la hipótesis nula y se concluye que los errores del modelo SARIMA tienen una distribución normal.
Con los resultados anteriores, se verifica entonces el cumplimiento de los supuestos sobre los errores para el modelo 2 - SARIMA; por lo tanto, se considera que los errores del modelo SARIMA son ruido blanco y el modelo 2 puede utilizarse para pronosticar.
C. Modelo 3 - modelo Holt Winters
El modelo 3 utiliza el método de suavizamiento de Holt Winters, dicho método se basa en los aportes de Holt (1957) quién propuso un método para datos estacionales y de Winters (1960) quien lo estudió posteriormente. El método Holt Winters se basa en la solución de tres ecuaciones: una para el nivel, una para la tendencia y la última para la estacionalidad (que puede variar de acuerdo con si la estacionalidad se considera aditiva o multiplicativa). Para la serie de consumo eléctrico del sector de explotación de minas y canteras se identificó la existencia de tendencia y estacionalidad (ver figura 1); las ecuaciones para un modelo con tendencia y estacionalidad modelada de forma aditiva se presentan a continuación:
Nivel:
Tendencia:
Estacionalidad:
Una vez se calculan las ecuaciones (4), (5) y (6), para nivel, tendencia y esta-cionalidad respectivamente, el pronóstico de la serie modelada con Holt Winters se realiza de acuerdo con la ecuación (7)
Pronóstico:
Los parámetros ajustados (α,β,y) usados para la serie de datos del consumo de energía eléctrica del sector minas y canteras de Colombia son: α =0,364; β =1e-4 ; y=0,066. El modelo Holt Winters resultante presentó un criterio de Akaike (AIC) de 973,070 y un criterio de Información Bayesiana (BIC) 1010,575.
Para verificar el cumplimiento de los supuestos sobre los errores del modelo 3 se utilizaron gráficas y pruebas de hipótesis. La figura 8 presenta la gráfica de los residuales, donde puede identificarse que su dispersión indica un comportamiento homocedástico en los errores.

Fuente: Elaboración propia utilizando (R Core Team, 2017).
Figura 8 Gráfico de residuales (εt) del modelo 3 - Holt Winters.
Por otro lado, la figura 9 presenta la función de autocorrelación (fac) de los errores del modelo Holt Winters, puede observarse como se encuentran dentro de las bandas de Barlett indicando la ausencia de correlación en los errores; esta conclusión se verifica utilizando la prueba Ljung-Box.
Hipótesis: H0= εt son incorrelacionados vs H α = εt son correlacionados
Criterio de rechazo: Vp < 5%
El valor p de la prueba Ljung-Box es de 0,410 considerando 24 rezagos, por tanto, no se rechaza la hipótesis nula y se concluye que los errores del modelo 3 no presentan correlación.
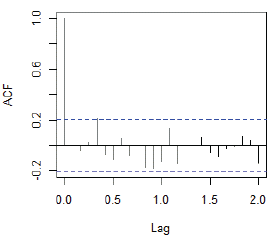
Fuente: Elaboración propia utilizando (R Core Team, 2017).
Figura 9 FAC para los residuales (εt) del modelo 3 - Holt Winters.
Finalmente, la figura 10 presenta la gráfica Q-Q utilizada para validar el supuesto de normalidad, dado que los puntos se ajustan a la recta, se concluye que los residuales tienen un comportamiento normal. Para esta afirmación se presenta también la prueba formal:
Hipótesis: H0= Et distribuye normal vs H α = εt no distribuye normal
Criterio de rechazo: Vp < 5%
El valor p de la prueba Shapiro-Wilk de normalidad es de 0,293, por tanto, se acepta la hipótesis nula y se concluye que los errores del modelo 3 tienen una distribución normal.
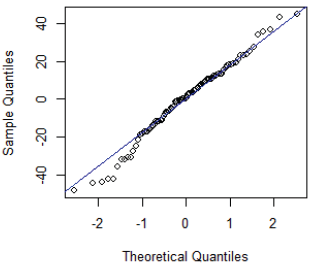
Fuente: Elaboración propia utilizando (R Core Team, 2017).
Figura 10 Gráfico Q-Q para los residuales (εt) del modelo 3 - Holt Winters.
Se concluye, entonces, que los errores del modelo Holt Winters son ruido blanco pues cumplen con varianza constante, incorrelación, y normalidad; por tanto, el modelo 3 puede utilizarse para pronosticar.
La Tabla 4 resume la información presentada en la sección 3 incluyendo los modelos ajustados, si estos resultaron significativos para explicar el comportamiento de la variable demanda eléctrica del sector de explotación de minas y canteras, y los resultados de la validación de supuestos sobre los errores teniendo en cuenta normalidad, varianza constante e incorrelación. Se identifica que todos los modelos resultaron significativos y útiles para pronosticar la serie de tiempo estudiada.
4. Resultados y discusión
Con el fin de encontrar un modelo de series temporales que permita pronosticar el consumo de demanda eléctrica del sector colombiano de minas y canteras, en este trabajo se ajustaron y validaron tres modelos utilizando la metodología de series temporales, incluyendo un modelo aditivo de componentes, un SARIMA y un modelo de suavizamiento Holt Winters.
Una vez ajustados los 3 modelos y verificado el cumplimiento de los supuestos sobre los errores, se concluye que los tres modelos encontrados pueden ser utilizados para pronosticar la serie de consumo eléctrico estudiada; por tanto, se procede a realizar los pronósticos para los últimos 12 datos reales de la serie, desde el mes de julio de 2017, hasta el mes de junio del 2018, correspondientes a las observaciones 91 a 102. Posteriormente, se calculan los criterios de error de pronóstico MAPE, MAE Y RMSE con los que se compara el desempeño de los diferentes modelos en cuánto a la exactitud de su pronóstico.
La figura 11 presenta los datos pronosticados con el modelo de componentes (Modelo 1), SARIMA (Modelo 2), Holt Winters (Modelo 3); y los últimos 12 datos reales de la serie (Observado).
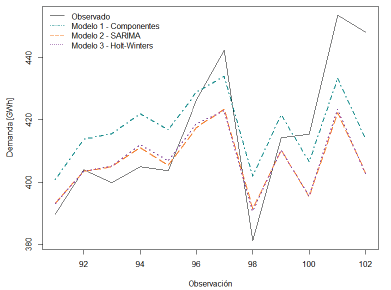
Fuente: Elaboración propia utilizando (R Core Team, 2017)
Figura 11 Comparación gráfica de los pronósticos con los tres modelos y los datos observados (conjunto de prueba).
Puede identificarse que el ajuste hecho con el modelo de suavizamiento (modelo 3- Holt Winters) es el que mejor describe el comportamiento de los datos reales, pues gráficamente se aproxima más al comportamiento de los datos observados (línea continua). Sin embargo, en los tres modelos se observa una subestimación del último dato pronosticado, lo que indica que ninguno de los tres modelos logra capturar completamente ese cambio de comportamiento que se observa en los últimos datos reales del período analizado.
La Tabla 5 presenta la comparación de los tres modelos de acuerdo con los criterios de precisión en los pronósticos MAPE, MAE Y RMSE, con el fin de brindar criterios objetivos para la selección del mejor modelo.
Tabla 5 Medidas de precisión en los pronósticos.
| Indicador | MODELO 1-COMPONENTES | Modelo 2 - SARIMA | Modelo 3 -Holt Winters |
|---|---|---|---|
| MAPE [%] | 3,390 | 3,170 | 3,010 |
| MAE [GWh] | 14,123 | 12,987 | 12,976 |
| RMSE [GWh] | 16,549 | 18,444 | 18,339 |
Fuente: Elaboración propia utilizando (Stoffer, 2012; R Core Team, 2017).
Los tres criterios utilizados, MAPE, MAE Y RMSE, son mejores mientras presenten valores más pequeños; por tanto, el modelo 3 - Holt Winters, es el que presenta los mejores resultados de acuerdo con dos de los tres criterios. Lo anterior significa que el modelo 3 brinda pronósticos más precisos, es decir, sus pronósticos son los que más se acercan al valor real guardado en el conjunto de prueba.
En términos cuantitativos, los resultados indican que la desviación de los datos es de 18,339 GWh, y que el error absoluto medio de pronóstico con el modelo Holt Winters es de 12,976 GWh. En términos porcentuales, el modelo Holt Winters, que es el mejor de los tres modelos ajustados, presenta un 3,01% de error según el criterio MAPE.
Al comparar los resultados obtenidos en este trabajo con los modelos existentes en la literatura para el caso colombiano (ver Tabla 1), se encuentra que el nivel de precisión del modelo desarrollado es comparable con los trabajos previos, siendo en algunos casos el MAPE mucho más bajo respecto a los demás modelos. Ahora bien, algunos de los modelos identificados en la literatura presentan un desempeño superior, es decir un nivel de error más bajo, pero ninguno de estos modelos fue diseñado para capturar las particularidades de la demanda eléctrica del sector no residencial de minas y canteras. En este sentido, este trabajo hace una importante contribución a la literatura, ya que proporciona el ajuste y validación de un modelo estadístico que permite explicar los fenómenos subyacentes al comportamiento del consumo de uno de los sectores más representativos en el mercado eléctrico colombiano con un bajo nivel de error.
Finalmente, no se descarta que, haciendo uso de otras técnicas de pronóstico como redes neuronales o inteligencia artificial, o haciendo combinación de estas técnicas con las series temporales o con la inclusión de variables exógenas que afecten el consumo en el sector de explotación de minas y canteras, puedan obtenerse mejores resultados para este tipo de estudios.
5. Conclusiones
Los modelos de pronóstico son herramientas útiles en la planeación estratégica, tanto desde la perspectiva de gobierno, como para la empresa y el consumidor final. En este trabajo se analizaron tres diferentes modelos de pronóstico para la demanda del sector de explotación de minas y canteras en el mercado eléctrico colombiano; el cuál se considera un sector importante debido a su gran participación en la demanda total de los sectores no residenciales en el mercado eléctrico colombiano, y por ser un sector de importancia estratégica nacional.
Para esta serie se ajustó un modelo aditivo de componentes y errores autorregresivos de orden dos, un modelo SARIMA y un modelo Holt Winters. Se encontró que los tres modelos cumplieron con los supuestos sobre los errores, por lo tanto, son adecuados para realizar pronósticos.
Se identificó que el modelo de suavizamiento Holt Winters presentó menor nivel de error, siendo éste en términos porcentuales alrededor del 3%; lo que en términos de unidades de consumo de energía equivale a una dispersión de 18,339 GWh que, aunque puede ser tolerable para evidenciar comportamientos y tendencias de mediano y largo plazo (perspectivas en períodos de un año), podría ser una dispersión significativa para la planeación estratégica detallada del sector.
Los resultados hallados en este trabajo contribuyen significativamente a la planeación estratégica del mercado eléctrico, pues aporta en la comprensión de las dinámicas de consumo de uno de los sectores no residenciales más representativos en la demanda eléctrica de Colombia, y favorece al desarrollo de instrumentos estadísticos y matemáticos para la toma de decisiones.
Finalmente, se destaca que este artículo cumple su objetivo al ajustar, validar y comparar tres modelos de pronóstico para la demanda eléctrica del sector colombiano de explotación de minas y canteras bajo la metodología de series de tiempo. Se resalta además que, en términos comparativos respecto a la literatura, los modelos desarrollados presentan un nivel de error aceptable, siendo en algunos casos mejor. Sin embargo, considerando que los hallazgos de este trabajo pueden ser útiles como insumo para la toma de decisiones estratégicas, y la gran relevancia del sector de minas y canteras, se sugiere proponer modelos adicionales con metodologías como redes neuronales u otras basadas en inteligencia artificial, o con la inclusión de variables exógenas explicativas, con el fin de identificar si es posible encontrar errores de pronóstico menores que podrían favorecer la precisión de los resultados.















