Introducción

Un objeto geométrico regular puede ser caracterizado en un plano de dos o tres dimensiones, en el primer caso se puede analizar la superficie y en el segundo el volumen. En cambio, un objeto de la naturaleza se caracteriza por su irregularidad, lo que ha implicado en la actualidad la necesidad de considerar nuevos conceptos y nociones matemáticas y geométricas que permitan medir esta irregularidad. La geometría fractal ha logrado tal finalidad, al proporcionar métodos para medir el grado de irregularidad de un objeto, mediante la dimensión fractal ¹. Los objetos de esta geometría reciben el nombre de objetos fractales, que por su configuración geométrica pueden ser deterministas o indeterministas (o estocásticos) como son los objetos de la naturaleza, que reciben el nombre de fractales salvajes ². La reproducción de este grupo de fractales, ha implicado introducir parámetros aleatorios, los cuales se caracterizan por generar modificaciones e irregularidades en su estructura ³. En la actualidad diferentes estructuras del cuerpo humano han sido caracterizadas desde el contexto de la geometría fractal. Uno de los métodos utilizados para medir el grado de irregularidad de un fractal salvaje, es el de Método de Box Counting ². Este método ha sido aplicado para caracterizar estructuras como son las arterias coronarias en un modelo experimental de restenosis, en ventriculogramas, células preneoplásicas y en las diferentes alteraciones de los glóbulos rojos ^4-11.

La variación en la forma del glóbulo rojo normal, implica un reporte de anormalidad en la muestra de extendido de sangre periférica, dando indicios de una posible enfermedad ¹². Dentro del grupo de trastornos hereditarios de los glóbulos rojos se encuentra la anemia de células falciformes o anemia drepanocítica. Se trata de una de enfermedad de origen genético de herencia autosómica recesiva caracterizada por la presencia de hemoglobina S en la cual ocurre una sustitución del aminoácido ácido glutámico por valina en la posición seis de la cadena β de la hemoglobina. Puede presentarse de manera homocigota (Hb SS) o heterocigota, presentándose varias combinaciones, tales como Hb AS, HbSC, HbS-Talasemia. Cuando disminuye la tensión de oxígeno, la hemoglobina S se polimeriza y los glóbulos rojos toman una forma falciforme o forma de Hoz o media luna característica. Esta forma favorece la oclusión de la microcirculación lo que da origen a una anemia hemolítica y crisis vaso-oclusiva dolorosa que causa la sintomatología propia de la enfermedad ¹³. Otra característica de los drepanocitos, es que son considerados causantes de la obstrucción del flujo sanguíneo cuando estos transitan por pequeños vasos ¹⁴. La comprensión de las alteraciones en la morfología de los glóbulos rojos, continúa siendo un problema clásico en la biología celular y en las últimas cuatro décadas también ha atraído la atención de otras ciencias para la ayudar a la identificación ¹⁵.

Teniendo en cuenta las consideraciones anteriores, se han propuesto nuevos estudios que plantean caracterizar la estructura irregular de las alteraciones de los glóbulos rojos ^6-11, sin las asociaciones morfológicas establecidas en los textos de hematología ¹⁶ en las que dichas células son equiparadas con figuras geométricas regulares como son el círculo, la elipse, la esfera, entre otras; logrando establecer una metodología diagnóstica para los glóbulos rojos y sus alteraciones, mediante la diferenciación lograda para los eritrocitos normales y sus diferentes alteraciones ⁶, así como para los equinocitos y esferocitos ^7-11 a partir de los espacios ocupados con la rejilla Kp, la superficie de cada célula y la proporción entre la superficie y la rejilla Kp. Después de lo anteriormente expuesto, el presente estudio tiene como propósito realizar una caracterización en la geometría de las células falciformes, midiendo para ello los espacios ocupados por la superficie de estas células en el contexto de la geometría euclidiana y fractal en el espacio de Box Counting.

Metodología

Método de Box Counting: se trata de un procedimiento matemático diseñado para calcular la dimensión fractal de fractales salvajes. Se consideran en este estudio las células falciformes como parte de este grupo de fractales. El cálculo se establece mediante la siguiente ecuación (ver Ecuación 1):

Siendo K el grado de partición de la cuadrícula (o rejillas), N el número de espacios que contiene el contorno del objeto y D la dimensión fractal.

Rejillas de 5x5 y 10x10 píxeles: se trata de un conjunto de cuadros diseñado en píxeles, en donde la cuadrícula de 5x5 píxeles, se denomina rejilla de cuadros pequeños (Kp) y la cuadrícula de 10x10 píxeles, rejilla de cuadros grandes (Kg).

Superficie (S): representa el número de píxeles que tocan el interior de la imagen de las células falciformes.

Procedimiento

Se realizó un reconocimiento de 30 imágenes de células falciformes en frotis de sangre periférica. Estas imágenes fueron reconocidas en el laboratorio de Hematología de la Universidad Colegio Mayor de Cundinamarca, según los criterios morfológicos de la célula.

La técnica de tinción utilizada para observar los glóbulos rojos fue colorante de Wright. El microscopio utilizado para hacer el reconocimiento fue con Olympus con un objetivo de 100x y un aumento ocular de 10x. Las imágenes de células falciformes fueron tomadas por una Cámara Canon de microscopio digital. Posteriormente, todas las fotografías fueron editadas en Microsoft Office Professional Plus 2010, con el fin de que todas tengan una misma escala de medida de 500 x 333 píxeles.

A continuación, fue delineado el contorno de cada una de las células falciformes tal y como se puede observar en la Figura 1. Seguidamente, fueron superpuestas las dos rejillas, para calcular mediante el método de Box Counting simplificado, el espacio ocupado por las células falciformes y posteriormente establecer su dimensión fractal (ver definiciones y Figura 2). La caracterización de las células falciformes se realizó a partir de los espacios ocupados por cada una de las células al superponer la rejilla Kp, tal y como se ha realizado en otros estudios ^9-11. Adicionalmente, fueron considerados los valores en píxeles de la superficie de cada célula y la proporción entre la superficie y los cuadros ocupados por las células falciformes al superponer la rejilla de cuadros pequeños (S/Kp).

Figura 1 Imagen de extendido de sangre periférica que corresponde a la célula falciforme No. 1 y No. 20. a) La flecha indica una célula falciforme reconocida y seleccionada para ser medida; b) la célula falciforme delineada; c) célula falciforme delineada y separada del resto de los eritrocitos que aparecen en la imagen. 

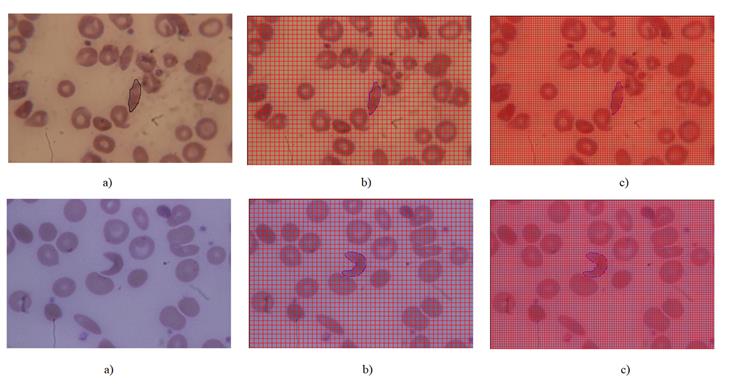
Figura 2 Superposición de rejillas Kp y Kg, en el extendido de sangre periférica en donde se encuentra la célula falciforme No. 1 y No. 20. a) célula falciforme seleccionada y delineada; b) superposición de la rejilla Kg (10 x 10 píxeles) en la célula falciforme; c) superposición de la rejilla Kp (5 x 5 píxeles) en la célula falciforme delineada. 

Resultados

Los espacios ocupados por las células falciformes con la rejilla Kp variaron entre 36 y 56, con la rejilla Kg entre 17 y 29. La dimensión fractal de las células falciformes varió entre 0.726 y 1.152 (ver tabla 1). La superficie de las células falciformes varió entre 969 y 1872 píxeles y la proporción entre S/Kp varió entre 23.1 y 39.6. El análisis de los resultados revela que los espacios ocupados al superponer las dos rejillas y la superficie de las células falciformes permite hacer la caracterización de las células falciformes. En cambio, los valores individuales de la dimensión fractal en el presente estudio no permiten caracterizar las células. Un ejemplo de esto se puede observar en los valores de la dimensión fractal de la célula falciforme No. 4 y 9 de la Tabla 1 cuyo valor de la dimensión fractal dio como resultado 1,000. Al observar los espacios ocupados por las células al superponer la rejilla Kp y Kg arroja valores distintos, evidenciando una vez más por qué no se considera los valores de la dimensión fractal para hacer distinciones matemáticas y geométricas en este tipo de estructuras.

Donde, Kp: es en número de cuadros ocupados por las células falciformes al superponer la rejilla de 5 x 5 píxeles. Kg: es en número de cuadros ocupados por las células falciformes al superponer la rejilla de 10 x 10 píxeles. Df: es la dimensión fractal; S: superficie en píxeles. S/Kp: la proporción entre la superficie y el número ocupados con la rejilla Kp.

Las Figuras 1 y 2 permiten observar los pasos previos que son requeridos para aplicar el método de Box Counting, el cual consiste en delinear la célula, para posteriormente superponer las dos rejillas (Kp y Kg), para el cálculo de la dimensión fractal. Se tomaron como ejemplo las imágenes de las células falciformes 1 y 20 de la Tabla 1, para detallar paso a paso la aplicación del método de Box Counting.

Discusión

Este es el primer trabajo que caracteriza el grado de irregularidad de las células falciformes, mediante los espacios ocupados al superponer la rejilla Kp, los valores de la superficie y las proporciones S/Kp, a partir de una metodología fundamentada en el contexto de la geometría fractal y euclidiana. En la literatura médica es muy común encontrar la asociación de la célula falciforme o drepanocitos con la forma que tiene una herramienta agrícola denominada ‘hoz’, para diferenciar esta célula del resto de alteraciones en la forma de los eritrocitos. En cambio, el presente estudio realizó una caracterización matemática directa con la forma irregular de estas células mediante los espacios ocupados por la superficie de estas células en el contexto de la geometría euclidiana y fractal en el espacio de Box Counting. Los resultados de este estudio contribuyen a generar un nuevo sistema de medida que faciliten el reconocimiento de estas células en muestras de sangre periférica.

La caracterización de las diferentes alteraciones en la morfología de los glóbulos rojos en el contexto de la geometría fractal y euclidiana, fueron posibles de realizar en la medida que se encontraron patrones matemáticos diferenciadores para cada una de estas irregularidades, lo cual contribuye a precisar el reconocimiento de estas diferentes alteraciones ^6-11. Desde esta nueva línea de investigación se encontró que los espacios de ocupación de los esferocitos evaluados con la rejilla Kp son menores al ser comparados estos valores con los espacios de ocupación de los glóbulos rojos normales. Adicionalmente se encontró que los valores de las proporciones S/Kp de estos dos tipos de glóbulos rojos permiten establecer diferencias matemáticas y geométricas ¹¹, y no los valores de la dimensión fractal tal y como se ha encontrado en estudios previos ^6-11. Esta primera caracterización realizada en la forma de las células falciformes es el primer aporte al área de la hematología con la cual se pueden refinar los estudios llevados a cabo en el reconocimiento de este tipo de células. En un futuro estudio se planteará la realización de una comparación matemática entre los glóbulos rojos normales y las células falciformes con el fin de establecer diferencias geométricas y matemáticas entre ambas células mediante los espacios de ocupación y las proporciones S/Kp.

Describir los hematíes según su tamaño, con los métodos clásicos de hematología requiere de mucho tiempo para su aplicación diaria ¹⁷. Uno de los primeros estudios propuestos para medir el tamaño de los eritrocitos fue diseñado por Price-Jones, en el cual estableció una técnica que buscaba un patrón que caracterizara la heterogeneidad de los diámetros de los eritrocitos, y de esta manera se estableciera un medio para evaluar la forma de los glóbulos rojos en la salud y la enfermedad ^17-19. En los analizadores de hematología se realiza un conteo sanguíneo completo automatizado, en estos analizadores se calcula el ancho de distribución de los glóbulos rojos, y es uno de los parámetros de rutina más disponibles. Este parámetro indica la variación en el volumen de glóbulos rojos y en su empleo se pueden detectar grados sutiles de anisocitosis ¹⁹. Sin embargo, algunos estudios han mostrado discrepancias en las interpretaciones de estos resultados ¹⁹.

El reconocimiento de la morfología celular es uno de los principios claves en la formación de los futuros profesionales. Desde esta perspectiva, un estudio llevado a cabo en 47 pacientes con anemia de células falciformes, describieron la forma de las células como redondas u ovales, un número variable de células de forma irregular, alargadas y estrechas con extremos redondos o puntiagudos ²⁰. Los resultados del presente estudio revelan la posibilidad del reconocimiento de las diferentes alteraciones de las células falciformes, a partir de la caracterización matemática de su forma irregular, permitiendo tener una medida cuantitativa, mejorando las caracterizaciones cualitativas logradas mediante analogías con figuras euclidianas. Esto permitirá al especialista caracterizar la estructura irregular celular de forma directa, evitando realizar caracterizaciones basadas en simulaciones de estas estructuras, que en la mayoría de los casos se alejan de la realidad del objeto medido.

En el espacio generalizado de Box Counting, se ha logrado caracterizar la morfología de otras estructuras como son los diferentes grados de alteración en las células de cuello uterino y establecer posteriormente metodologías diagnósticas de aplicación clínica ²¹. También se ha caracterizado arterias coronarias normales hasta re-estenosis en un modelo experimental de porcino ⁴. De igual modo, el comportamiento de la dinámica cardiaca de adulto y neonatal simulada mediante atractores cardiacos, los estados de normalidad y anormalidad, así como la evolución a estos agudos, han sido diferenciados a partir de los espacios que ocupa el atractor cardiaco ^22,23. Desde esta línea de investigación se ha logrado establecer los primeros parámetros matemáticos que predicen casos mortalidad analizando el comportamiento de la dinámica cardiaca ²⁴. También, se han logrado predicciones en otras áreas como son la biología molecular ²⁵, la epidemiologia ²⁶ y la infectología ²⁷.