Introduction
With increasing coal mining depth, the hydrogeological conditions of mines are becoming increasingly complex, and coalmine water inrush disasters are a serious threat to the safe operation of coal mines (Wu, 2014). The mine transient electromagnetic method considers proximity to the target for exhibiting a strong signal response and high resolution, this is widely used in the prediction of goaf water, column collapse, and mine disasters (Cheng et al, 2016; Danielsen et al, 2003; Huang et al, 2017; Wang et al, 2017a; Wang et al, 2017b). However, transmission and receiving devices used by the mine transient electromagnetic method are located in underground roadways and hence, the received signal is a superposition of various low-resistance electromagnetic induction signals within the detection range. Thus, distinguishing water body information from these signals for practical applications is difficult (Chang et al, 2016; Su et al, 2017; Xue & Yue, 2017; Zhou et al. 2014). Therefore, studying the influence of metal supports in the roadway on mine transient electromagnetic detection is important for eliminating metal interference and determining the distribution range of water-containing anomalies.
Many researchers have conducted experimental studies on the mine transient electromagnetic method considering metal interferences (Liu et al, 2016; Jin & Wang. 2018, Qin & Zhao. 2019, Zhou et al. 2014); however numerical calculations of these phenomena have rarely been conducted. The direct time-domain finite difference method can directly simulate the propagation and diffusion of electromagnetic waves and can be used to analyze transient electromagnetic field signals (Yan et al, 2002; Yue et al, 2008). According to the Maxwell equations and finite-difference principle, the metal support in the roadway can be considered as a thin layer of metal, and the finite difference iterative equation of this thin metal layer can be derived. The transient electromagnetic field under the influence of the metal roadway support can also be derived based on the finite-difference equation. This simulation was performed to study the electromagnetic field diffusion characteristics under the influence of a thin metal layer and generate a full-space transient electromagnetic response curve under the influence of these thin metal layers with different thicknesses. In addition, the transient electromagnetic response of the water-containing low-resistance structural model under metal the influence of the metal layer was analyzed.
Principles of the Finite-Difference Numerical Simulation
Quasi-static Maxwell's equations
where, H ( r, t ) is the magnetic field strength, E (r, t) is the electric field strength, a (r )is the dielectric conductivity, and u is the magnetic permeability. A passive diffusion equation for the electric field can be obtained.
Under 2D conditions, two infinitely long wires with positive and negative currents were used as the emission source and placed along the Y-axis. Thus, the induced electric field has only a y component and the magnetic field strength has only x and z components. Figure 1 shows the two-dimensional finite-difference meshing mode where point E i, j and its surrounding E i+1,j , , E i,j +1 , , E i,j, +1 , E i,j, +1 constitute a five-point difference format (Liu. 2014).
Connecting the center points of the four small rectangles around Ei j forms a rectangle, ABCD. At any time, Equation 2 can be integrated into the rectangle ABCD to obtain Equation 3 as follows:
The difference equation of the diffusion equation can be obtained According to Green's formula and the central difference method.
where,
Finite-Difference Simulation of the Metal Sheet
Metal supports can affect electromagnetic wave propagation, in turn affecting the detection results (Yu et al, 2008). For numerical simulations, local fine mesh or subdomain algorithms are generally used for thin lamellar bodies (Elsherbeni & Demir, 2006; Sun et al. 2013). However, the net thickness of the metal anchor is much smaller than the grid size and its resistivity is much smaller than the surrounding resistivity of the Earth. Thus, it is difficult to perform numerical simulations using conventional methods. Therefore, a finite-difference iterative formula applicable to the metal structure must be derived.
Yan and Shi (2004) derived the finite-difference iterative formula for thin wires by considering railroad tracks as thin wires. In this study, we consider the metal support to be a thin layer of metal with a finite thickness. The relationship between the electromagnetic field in the thin metal layer and the surrounding electromagnetic field can be derived using the Maxwell equation boundary conditions. Figure 2 shows the finite difference model of a thin layer of metal along the X-Z plane (Liu. 2014).
The integral form of the two rotation equations in Equation 1 can be written in the form of a difference equation.
where
 is the average conductivity within the rectangle, ABCD. Because the conductivity of the thin metal layer is much higher than that of the surrounding medium, the conductivity of the earth medium in ABCD can be neglected as follows:
is the average conductivity within the rectangle, ABCD. Because the conductivity of the thin metal layer is much higher than that of the surrounding medium, the conductivity of the earth medium in ABCD can be neglected as follows:
where σ is the conductivity of the metal and d is the thickness of the metal layer. For the metal support, d should have an equivalent thickness. Because of the influence of the metal layer, the magnetic field strength-x component H x -increases on both sides of the metal layer, and the magnetic field strength-z component H z -is continuous. Thus, the second term on the right side of Equation 7 can be neglected and the equation can be written as follows:
Substituting Equations 5 and 6 into Equation 9 yields:
The time derivative can be written in the form of a central difference:
Linear interpolation of E n i ,j
By substituting Equations 11 and 12 into Equation 10, the difference equation of the thin metal layer in Figure 2 can be obtained.
Where
For the metal layer along the X-Y plane, the difference equation can be obtained as follows:
Equations 13 and 14 are the finite difference iterative equations for the thin metal layers.
Numerical calculations
Transient electromagnetic field distribution under the influence of the metal layer
According to the principle of finite difference, using Equations 4, 13, and 14, the full-space transient electromagnetic field under the influence of the metal support was simulated using the absorbing boundary condition (Yang & Yue, 2009). Figure 3 shows the 2D space model used herein. The resistivity of the model was 50Ω- m with a roadway width of 20 m, the launching point was at the center of the roadway. The two long wire sources were placed along the Y-axis, while the normal direction was specified along the X-axis, space was 2 m, the emission current was 10A, and the metal mesh was set to a diameter of 5 mm- commonly used for the equivalent metal layer-which has an equivalent thickness of 0.2 mm.
Figure 4 shows the transient electric field contour map as a function of time with and without the metal support, where the electric unit is y/m , and the horizontal line in Figure 4 represents the roadway boundary. Figures 4a and 4b show the electric field contour maps with and without the metal support, respectively, at t = 0.64 us. Here, the transient field which appears as a 'smoke ring' did not spread to the roadway boundary, the metal support at the boundary of the roadway compressed the electric field periphery. Thus, the metal support of the roadway affected the electric field distribution. Figure 4c and d show the electric field contour maps with and without metal support, respectively, at t = 2.21 us. Here, the 'smoke ring' without support reached the boundary of the roadway, whereas when support was present, the electric field became distorted at the boundary of the roadway. The presence of a thin layer of metal reduced the rate of electric field diffusion, squeezing the "smoke ring" at the metal boundary of the roadway. Figure 4e and f show the electric field contour maps with and without the metal support, respectively, at t = 7.87 us. Here, the "smoke ring" without the support crossed the boundary of the roadway, whereas, with the support present, the 'smoke ring' remained at the boundary of the roadway and did not shift forward to a significant degree. This is due to the low resistivity of the thin metal layer (<10-6). Thus, the transient field diffused very slowly (Yu et al, 2008).
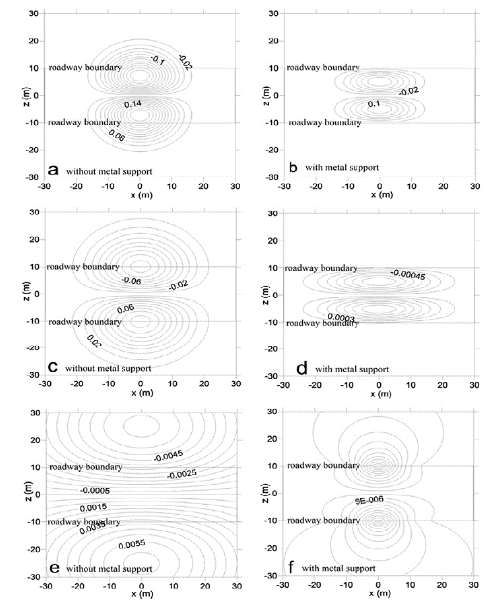
Figure 4 Transient electric field contour map at different times with and without the metal support.
Therefore, it can be concluded that the roadway metal support will greatly reduce the diffusion speed of the transient field, inevitably affecting the actual detection results.
According to the relationship between the vertical induced electromotive force and electric field in the receiving coil per unit area, the electric field can be converted into a magnetic field as a function of time as follows:
Figure 5 shows the transient electromagnetic response curve influenced by the different thicknesses of the metal support. The observation point was located at the launch point and the wire diameter of the metal support net was varied at 2, 5, and 7 mm with equivalent thicknesses of 0.03, 0.2, and 0.4 mm, respectively. From Fig. 5 it is clear that the response value with the metal support is significantly higher than that without the support, with a maximum value that differed by three orders of magnitude. Moreover, after 2 ms, increasing the equivalent thickness of the metal support layer resulted in higher response values. Initially, the response in the presence of the metal support is slowed. However, over time the decay rate gradually increases and the curve moves gradually closer to that of the unsupported curve, showing consistency with the physical simulation.
Numerical simulation of a model with low resistance anomalies
The mine transient electromagnetic method is mainly used to detect water-containing, low-resistance anomalous structures. To further study the effect of metal supports on the transient electromagnetic response, the response of a water-containing low-resistance structural model was simulated. Here, the abnormal body resistivity was set to 1 Ω-m for a size of 10 m x 10 m. The model was located below the field source, 50 m away from the floor of the roadway, and the resistivity was set to 50 Ω - m . A metal mesh with a diameter of 5 mm was selected with an equivalent thickness of 0.2 mm. The simulation results are shown in Figure 6 where the ordinate indicates the relative apparent resistivity Pr (Chang et al, 2020). The relative apparent resistivity is defined as the ratio of the apparent resistivity in the presence of an abnormal body to that without an abnormal body,
where Pτ is the apparent resistivity without any low resistance anomalies and Pτ is the apparent resistivity with a low resistance abnormality.
Figure 6 shows that without the metal support, the relative apparent resistivity curve begins to decrease at t= 0.08 ms, and a low-resistance anomaly occurs. However, in the presence of metal support, an abnormality occurs at t= 3 ms, indicating that the metal support delayed the transient electromagnetic response. Thus, when the abnormal body is at the same position, observed longer observation time is required in the presence of metal support. In Figure 6, without the metal support, the low resistance abnormality caused the curve to drop to 0.32, whereas in the presence of the metal support, the lowest point of the curve was 0.90. This indicated that the metal layer reduced the sensitivity of the transient electromagnetic method and weakened its reaction to the low resistance abnormal body.
Therefore, in the actual exploration process, there should be a special focus on the interference of the surrounding metal environment and this work should be fully recorded. In the data interpretation process, it is necessary to perform time-sharing corrections on the exploration data according to the collected time series.
Conclusions
By using a numerical simulation method to simulate the effect of metal support on TEM detection, the following conclusions are drawn.
1) The metal anchor net support was treated as a thin metal layer and the finite difference equation of the metal layer was derived. A non-uniform grid was used to simulate the transient electromagnetic response characteristics of the entire space under the influence of the metal layers. The presence of a thin metal layer slowed the transient field diffusion rate and hindered the overall diffusion of transient electromagnetic fields.
2) The magnetic field as a function of the time derivative parameter curve observed under the influence of the thin metal layer was higher than that of the response curve without the metal support. Increased thickness of the thin metal layer resulted in higher curves.
3) Simulation of the transient electromagnetic response of the water-containing, low-resistance anomaly model showed that the metal support layer delayed the transient electromagnetic response, requiring longer times for observation. Moreover, the metal support reduced the sensitivity of the transient electromagnetic method and weakened the reaction to the low-resistance anomaly. Therefore, performing relevant corrections during the actual exploration process is necessary.



































