Introduction
Today, Global Navigation Satellite Systems (GNSS) play a major role to extract high-accurate and four-dimensional (4D; x, y, z+t) geo-referenced positioning information. Among these systems, Global Positioning System (GPS), owned and operated by United States (US) has still dominant specifications by ongoing modernization facilities. Until now, GPS has been used for a wide-range geodetic/geomatics studies, such as deformation monitoring, precise navigation, geodetic networks, cadastral applications, hydrographic surveys, geographical information systems (GIS), photogrammetric studies based on kinematic GPS, terrestrial-mobile-airborne LIDAR applications, remote sensing, unmanned aerial vehicle (UAV) systems, early warning system configurations for detecting natural disasters such as earthquakes, landslides, meteorological studies, which require high precision positioning information (Ocalan et al., 2016). As commonly known, GPS enables to estimate three-dimensional precise positioning, navigation and timing facilities (Hofmann-Wellenhof et al., 2008; Gao, 2018; Erdogan et al., 2018; Zhou et al., 2019). The improvement in accurate positioning is an ongoing issue that mostly deals with modeling the error sources. Besides that, the researches about environmental issues have become more significant than before because of the climate change that affects the whole world. Especially accurate estimations of the underground water level, snow package volumes, tracking the vegetation grow, soil moisture have become crucial issues. Recently, many scientific researches have been conducted to detect the contributions of these items to the climate system with a novel methodology called, GPS interferometric reflectometry (GPS-IR) method, which provides significant and effective outcomes for these studies (Ozeki & Heki, 2011; Gutmann et al., 2012; Larson & Nievinski, 2013; Larson et al., 2009a; Chew et al., 2016; Larson et al., 2009b; Roussel et al., 2015; Roussel et al., 2016; Nievinski & Larson, 2014a).
Precise point positioning in GPS needs to eliminate or model the error sources. Although one of the major error sources so called multipath, affects the positioning accuracy, it has become an effective tool to extract environmental features. Signals reflected from the surface following one or more paths near a GPS receiver interfere with the direct signals while a composite signal is formed as the sum of them. The direct and reflected signals can simultaneously be recorded at the antenna of the GPS receiver. This interference creates significant oscillations, especially at low elevation angles. If the direct component of the signal is removed, the remaining part will be the reflected component of the signal.
The initial procedure of using reflected signals instead of direct signals was introduced by Martin-Neira (1993) to measure the ocean surface (Larson & Small, 2016). Besides, many studies have been conducted to retrieve surface specifications among the reflected signals. Larson et al. (2009a) show that variations in snow depth estimated by GPS-IR method agree very well with the in-situ measurements, which means that the method could be used successfully and high-correlated with the in-situ measurements for retrieving the effective reflector height (McCreight et al., 2014; Nievinski & Larson, 2014a; Nievinski & Larson, 2014b). Ozeki and Heki (2011) represent a geometry-free linear combination for the feasibility of analyzing multipath pattern in GPS data series and demonstrate that it could be also used for snow depth retrieving facilities. Gutmann et al. (2012) indicated the necessity of determination of the effective reflector height when the snow depth computation is indispensable for climatological studies in hydrological ecosystem and conducted a detailed study with nine-month period including winter season following GPS-IR methodology by validating the results both laser scanning data and in-situ measurements from snow poles, and found accurate results within 9 cm to 13 cm interval. Chen et al. (2014) used cost-effective dipole antenna instead of the geodetic antenna by analyzing L2C signals collected and showed an improvement in results when compared with the geodetic receiver for snow depth estimations. Hefty and Gerhátová (2014) examined SNR data of L1 and L2 carrier phases and the geometry-free linear combination of carrier phases, L4 for two permanent GPS stations data. The validation was performed with the regular manual snow depth measurements and it was demonstrated that better than 5 cm accuracy was mostly reached when comparing with the estimated reflector heights. Bilich et al. (2011) define the ground specifications of a good GPS-IR station as flat or slightly titled surface as lower than 5° ground slope, and previous studies show that implementing GPS-IR method to the horizontal, planar surface performs good results. However, a new strategy proposed by Wei et al. (2019), so-called Tilted Surface Strategy (TSS) exposed the slope effect of the topography to retrieve the snow depth and they concluded that following the TSS for receivers located on slopes works better.
In this paper, first a brief description of the multipath theory and the processing of SNR data following Larson and Nievinski (2013) are introduced. Then, the experimental site performed for accuracy assessment of the model by vertical shifting is applied and the results are presented. A snow-free environmental is demonstrated to retrieve the effective reflector height for the experimental test to mitigate the penetration effect of the GPS signals into the surface and the estimations with the RMSEs of vertical shifting values are computed.
Multipath Effect and SNR observations
Hofmann-Wellenhof et al. (2008) give the basic description of the multipath effect on carrier phases as receiving the satellite-emitted signal at the receiver by more than one path, caused by reflecting surfaces near the receiver in particular (Figure 1). Recently, multipath, as a major error source for GNSS precise point positioning, has become a key element for retrieving information from reflecting surface. Even though the antenna configuration of the GPS is designed to suppress this error source, that can not be removed totally (Larson et al., 2009b). The reflected signal contribution can be seen at low elevation angles, i.e. lower than 30°, due to antenna gain pattern (Larson & Small, 2016). Several studies have been exposed to the use of multipath data for estimating the parameters of reflecting surface. Besides that, the geometry of the reflecting signal allows computing the effective reflector height, which is extracted from where the signal reflects on the ground and arrives at the GPS antenna phase center (APC).

Figure 1 Multipath effect due to reflecting surface and converted vertical height from reflecting surface
The multipath effect means that the satellite signals don't reach the antenna center directly in one way, but some are reflected once or several times in advance on objects in the receiving environment or on the ground. The multipath effect is occurred both from the relation of the geometry of the reflecting surface and geodetic receiver antenna and the dielectric constant of the reflecting surface (Larson et al., 2009b). The reflected signals have always a longer transit time than the direct signal. That leads to an extended pseudorange determination between the antennas on the ground and the satellite. Since the phase of a wave is a function of the transit time, a longer transit time also affects the carrier phase measurement. Because objects on the surface of the earth mainly affect satellite signals with low elevations, signals from low-flying satellites are more affected by multipath effects than signals sent by satellites with high elevation. The amount of the error, which is caused by multipath effects, depends on the multipath length (the resulting delay of the signal travel time), the phase difference between direct and reflected waves and their power ratio.
The achievable accuracy of positioning using GNSS measurements depends on the detection of the stations (variations of the antenna phase center, multipath effect, receiver noise, receiver clock and receiver signal errors) and satellite-specific factors (satellite geometry, clock and orbit errors of the satellites, including GNSS Code and system bias, phase wind-up) The behavior of the signals of the GNSS satellites, which acts as high-flying fixed points at an average altitude of 20200 km, is influenced during the propagation in the various layers of the atmosphere (delay in the signals in the ionosphere and troposphere). Most of the error components that affect the accuracy of GPS are largely eliminated by the differentiation method by data processing. A good example of such an approach is RTK (Real-Time Kinematik) and Network-RTK, where error components of GNSS are calculated using data from one (RTK) or several reference stations (Network-RTK) in the surroundings of the rover and by a data transmission medium either as correction of coordinates or as values for corrections from the rover received satellite data made available in real-time. The rover uses these corrections to increase the accuracy of the positioning, This requires a service for the calculation and transmission of the corrections to the rover as well as for the permanent maintenance of reference stations within the network. From the mid-1990s, CORS (continuously operated reference station) networks were established in Europe and in certain regions of the world to provide the RTK and network RTK services.
Multipath effect, the cause of which lies only in the immediate surroundings of the antenna, cannot be therefore eliminated using the differential method, because multipath effects are uncorrelated even from a distance of a few meters between two antennas. The computation of multipath effects at reference stations are therefore very important with respect to the precise positioning using GNSS data, since a coordinate error at reference station also influences the determination of the correction data and thus falsifies the calculated coordinates of the rover. Therefore, the CORS of a network must be free of the multipath effect to reach the high quality for positioning.
Since any general model can be extracted for the multipath effect, the influence can be detected by code and carrier phase measurements (Hofmann-Wellenhof et al., 2008). However, the signal power of the composite signal formed by interfering with the reflected and direct signals can be affected as well. Multipath effects are also visible in the signal to noise ratio (SNR) data constantly collected by GNSS receivers (Roussel et al., 2015). Signal strengths are also stored in GPS receivers beside carrier phases. The signal strength corresponds to the carrier-to-noise density ratio (C/No), which is a ratio of signal power to noise power density (Larson & Nievinski, 2013). The SNR, computed from this ratio, is usually used for determination of signal quality and noise characteristics of classical GPS observations (Qian & Jin, 2016; Tabibi, Geremia-Nievinski, & van Dam, 2017). Since the SNR data are in the logarithmic unit in dB, they are converted to a linear scale in watt per watt (volt per volt) by SNR  =10SNR(dB-Hz/20), assuming a 1-Hz bandwidth (Larson & Nievinski, 2013). The SNR value recorded at a receiver is assumed to be equal to the amplitude of the received signal, then the equation equals the same quantity between SNR and amplitude of the composite signal. During the satellite movements across the sky, the phase difference between direct and reflected signals is formed, which is also represented as an interference pattern (Löfgren et al., 2014; Drosinos, 2016). The interference between these signals is directly related to the satellite elevation angle. Since, the satellite elevation angle increases, the multipath effect on SNR data decreases (Larson et al., 2008). As the signal transmitted from a satellite received at the antenna as a composite signal, interfere of direct and indirect signals, the relation between the signal to noise ratio can be expressed as Equation 1 (Larson et al., 2008; Larson & Nievinski, 2013; Nievinski & Larson, 2014a);
=10SNR(dB-Hz/20), assuming a 1-Hz bandwidth (Larson & Nievinski, 2013). The SNR value recorded at a receiver is assumed to be equal to the amplitude of the received signal, then the equation equals the same quantity between SNR and amplitude of the composite signal. During the satellite movements across the sky, the phase difference between direct and reflected signals is formed, which is also represented as an interference pattern (Löfgren et al., 2014; Drosinos, 2016). The interference between these signals is directly related to the satellite elevation angle. Since, the satellite elevation angle increases, the multipath effect on SNR data decreases (Larson et al., 2008). As the signal transmitted from a satellite received at the antenna as a composite signal, interfere of direct and indirect signals, the relation between the signal to noise ratio can be expressed as Equation 1 (Larson et al., 2008; Larson & Nievinski, 2013; Nievinski & Larson, 2014a);
Here, A d and A m are the amplitudes of direct and reflected signals (in volt unit), respectively and is the phase difference (in radian unit) between these signals. Assuming A d >> A m , the magnitude of the SNR is mainly caused by direct signal, a quadratic polynomial function can be used to remove the dominant part effect (Larson & Small, 2016). After removing this part, the remaining SNR value, as commonly expressed by detrended SNR (dSNR), can be described by Equation 2;
where A is the amplitude, Ψ is the phase offset, e is the satellite elevation angle, λ is the carrier wavelength, h is the distance between the antenna phase center (APC) and the reflecting surface (generally called as reflector height). As the multipath pattern can be expressed as a function of the sine of the elevation angle, that causes an unevenly spaced sampling intervals, the dominant frequency of the dSNR will be constant and equal to the 2M. Once the dominant frequency of the dSNR values is extracted, it can be converted to the reflector height, which is the distance between the APC and reflecting surface. Lomb Scargle Periodogram (LSP) is used to estimate the dominant frequency (Larson & Small, 2016). Since LSP spectrum analysis represents the power of the frequencies for the SNR series, the SNR data used are grouped into varied elevation angle ranges including noisy frequencies to control the effective reflector heights estimated with in-situ reflector measurements.
Materials and methods
Study area
The study aims to control the SNR data fluctuations on retrieving effective reflector heights by checking the vertical shift amount from them. For that, two stations, so-called ELK1 and ELK2 were established on the roof of the Faculty of Electrical and Electronics Engineering at the Davutpasa Campus of Yildiz Technical University in Istanbul. The two-dimensional metrics of the roof are approximately 12 m and 75 m. The roof surface can be accepted as quite flat avoiding the surface roughness, with the exception of the slightly elevated ground as wall border near the ELK1 station. Also, there are no high buildings near the roof that could obstruct the open sky view and make disturbing reflections. The representation of the locations of the stations on the roof is given in Figure 2 and the geographical coordinates are given in Table 1.
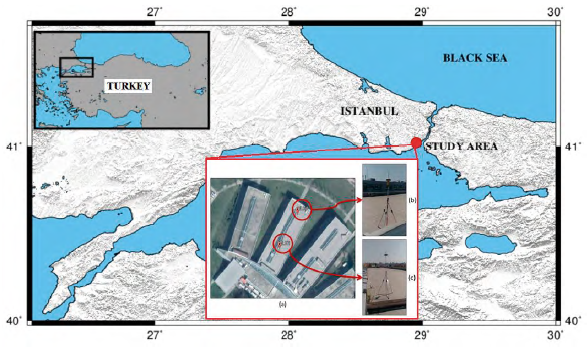
Figure 2 Study environment (a) Locations of the stations on the roof (b) ELK2 station-south direction (c) ELK1 station-east direction
Data acquisition
GPS observations were performed in an experimental field site with two observation stages. The first one was carried out on day of years (DoY) 203, 204, 205, 206, 207 and 210; and the latter on DoY 211, 212, 213, 214, 215 and 217. The starting and ending times and dates for observations are given in Table 2.
The receivers used in the first part were Topcon HiPer Pro at ELK1 and Topcon GR-5 at ELK2, and in the second part were CHC i70 at ELK1 and CHC i80 at ELK2, respectively. Moreover, the technical specifications of the used receivers are given in Table 3. Table 3 also covers the SNR evaluations of the collected data that are done for L1 carrier frequencies.
Table 3 Technical specifications of GNSS receivers and SNR data collected (e, satellite elevation angle)

GPS data were collected with a sampling interval of 1 sec. To detect the effective reflector heights on the site using GPS SNR data, a decrement as 10 cm assuming a vertical displacement occurred as an effect of changing the vertical distance was applied to both reflectors established on the stations. To do that, the observations were planned first to start from 2 m for the ELK1 station and 1.70 m for the ELK2 station, and then the reflector height was reduced by 10 cm in every two days by collecting daily data for at least 6 hours. The decrement is applied to simulate snow depth variations. In this study, only GPS observations were used. The data collected during the site surveys are split as ascending and descending according to variations of the satellite elevation angle. All the data were recorded by the GPS receivers, but the data for low elevation angles (5°-25°), where the major multipath effect was intense, were analyzed. In the analysis, observations, where the difference between the minimum and maximum elevation angles of each observed satellite during any satellite arc track is less than 10° are not taken into account. This 10° condition benefits from getting enough epoch numbers for each track. In the evaluations, the azimuth angle range of 30°-210°, where the roof surface is flat, was selected, and data from other directions were excluded due to the obstructs on the roof. Here, the azimuth angles except the selected range were not proper to analyze while considering the direction and width of the sensed areas on the roof. The sensed area, i.e., first Fresnel zone (FFZ), varies depending on the change of satellite elevation angle and reflector height (Larson & Nievinski, 2013). Due to that different reflector heights have been used to track the variation of the sensed area from FFZs. Figure 3 shows the FFZs for observations to the satellites at elevation angles 5° and 10° for reflector heights of 1.70 and 2 m in DoY 203.
Only SNR values of L1 signals were analyzed and used in this study. The statement given in Larson and Nievinski (2013) is used to identify the signals as a strong reflection, where the peak value on data series is higher than four times of background noise, for each ascending and descending arcs of the satellite tracks.
The signal that does not meet this condition is called weak reflection in this study. In this way, it has been found that 139 of the 371 signals have a strong reflection. Maximum critical reflector height converted from the LSP was taken as 10 m, which was important to estimate the strong reflection statement that can change the arithmetical mean value of A i .

Figure 3 FFZs at ELK1 and ELK2 in DoY:203 (a) for 5° elevation angle, 2.00 m reflector height (b) for 10° elevation angle, 2.00 m reflector height (c) for 5° elevation angle, 1.70 m reflector height (d) for 10° elevation angle, 1.70 m reflector height. Red ellipses are within the desired azimuth range while blue ellipses are outside that range. The radii of the nested circles indicating the distance from the point were drawn in increments of 10 m.

Figure 4 Four examples of dSNR values in DoY:211 (a) strong reflection at ELK1 (b) weak reflection at ELK1 (c) strong reflection at ELK2 (d) weak reflection at ELK2. Dashed lines are polynomial fits to the SNR data. The black lines show the SNR data, the blue dSNR in linear scale, the orange SNR in logarithmic scale and an example for (e) total C/No for both direct and multipath signals with satellite elevation angle
Results and Discussion
The examples of weak and strong reflections of dSNR values obtained from the analyses are represented in Figure 4. The examples of strong reflections shown in Figures 4a and 4c present sinusoidal trend for oscillations especially at low elevation angles. Since the multipath effect decreases with increasing the satellite elevation angle, the oscillations in the resulting signal become smaller. Thus, the oscillations become stable when the elevation angle increase. For the weak reflection examples, no strong periodic oscillation could be tracked (Figure 4b, 4d). Moreover, although the reflections between 5°-15° elevation angles did not show periodic oscillations, this situation has changed when the elevation angle interval is drawn for 15°-20° (see, Figure 4b and 4d). This can be caused by the location of the reflected signal that falls to the roof surface when the elevation angle increases.
The LSP was used to convert the SNR data to the effective reflector heights. Spectral amplitudes of each GPS track computed by LSP were evaluated by following Larson and Nievinski (2013). Then, the dominant frequencies are converted into effective reflector heights. Figure 5 shows the 6-day amplitude-reflector height values of strong signals for ELK1 and ELK2 stations.
The correlation coefficients (ρ) between estimations and in-situ measurements for reflector heights are shown in Figure 6. Moreover, the detailed information about the correlation coefficients calculated from estimated reflector heights and in-situ measurements calculated separately from receivers is given in Table 4. The highest correlation coefficient is computed at ELK2 station as 0.9346 for 46 estimations. Although the maximum estimation number, 49 is obtained at ELK2, the correlation coefficient is calculated as 0.8587, which is the lowest agreement with the in-situ measurements. This could be caused by the GPS instrument used (see, Table 3).
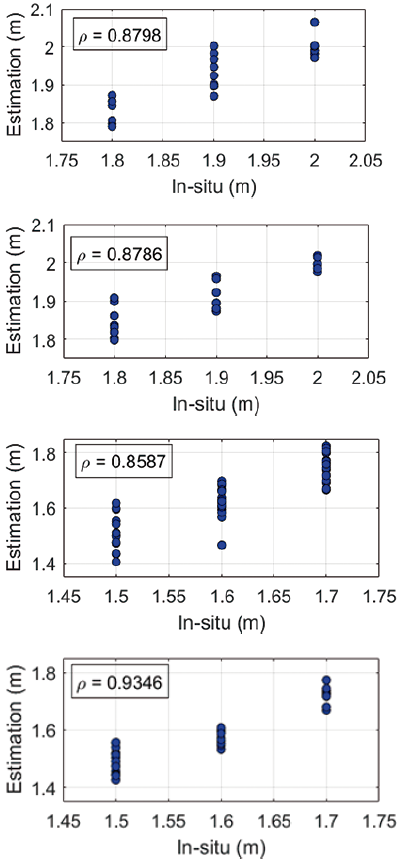
Figure 6 Correlation coefficients (a) Topcon HiPer Pro at ELK1 (b) CHC i70 at ELK1 (c) Topcon GR-5 at ELK2 (d) CHC i80 at ELK2
Table 4 Number of estimations and correlation coefficients for receivers
| Receiver | Number of estimations | Correlation coefficient |
| Topcon HiPer Pro (at ELK1) | 23 | 0.8798 |
| Topcon GR-5 (at ELK2) | 49 | 0.8587 |
| CHC i70 (at ELK1) | 21 | 0.8786 |
| CHC i80 (at ELK2) | 46 | 0.9346 |
The daily mean values of estimated reflector heights and root mean square errors (RMSE) with respect to DoYs are given in Table 5.
Here, the model efficiencies were estimated to figure out how the model fit the site observations considering the location of the points separately. Then, the accuracy of the model for ELK1 with TOPCON HiPer Pro receiver is computed as 2.7 cm, for ELK2 with TOPCON GR-5 receiver is 3.4 cm, for ELK1 with CHC i70 receiver is 2.8 cm, for ELK2 with CHC i80, receiver is 2.2 cm.
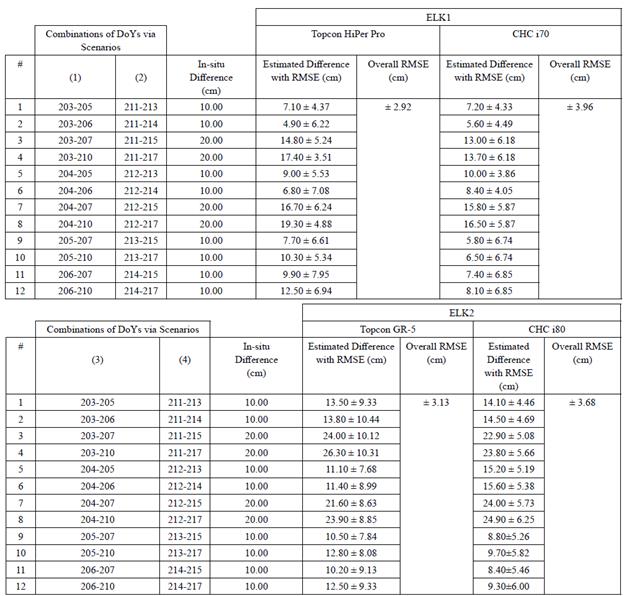
To verify the estimations with the vertical shift amount, assuming as constant in each couple of days, 12 different combinations were created for decrements of 10 cm or 20 cm. The RMSEs of estimated differences are computed from subtracting the in-situ differences from the differences in the mean of daily estimated heights. Table 6 represents the computed RMSEs of 12 combinations for four simulated scenarios. The overall RMSEs of ELK1 for scenarios 1 and 2 are calculated as ±2.92 cm and ±3.96 cm, respectively. Meanwhile, the overall RMSEs of ELK2 for scenarios 3 and 4 are calculated as ±3.13 cm and ±3.68 cm, respectively. These results agree with the RMSEs of the daily mean values of estimations. However, according to the RMSE computations of estimated differences (see Table 6, column 5 & 7), the RMSE values of some of the vertical shifts (the underlined cell) are greater than vertical shift values. This situation can be interpreted as they are statistically insignificant. Moreover, according to the results given in Table 5 and 6, there are slight differences between the RMSE values of estimations, which are arisen due to usage of different receivers.
Conclusions
In multipath theory, a signal transmitted from a satellite uses more than one path to arrive at the GNSS antenna. Here, the signal may be reflected from the surface around where the receiver is set. The reflected and direct signals, which interfere with each other at the phase center of the GNSS antenna, are recorded simultaneously. The multipath modulation can be observed in GPS observations as SNR values, which enable to estimate the vertical distance between the reflected surface of the signal and phase center of the GNSS antenna. Several studies have been conducted to estimate the reflector height to extract environmental variables, such as snow depth, vegetation height, etc. In this study, an experimental site was prepared to extract the effective reflector height with its accuracy assessment. The study involves GPS L1 SNR data due to provide strong signal strengths than the L2 and/or L5. To achieve varying reflector heights on the site, the reflector height is displaced manually in daily observations to detect artificial reflector height variations. The results indicate that the reflector heights and height differences between days given as 10 cm in each observation day agree with the daily in-situ measurements showing a high correlation with 0.9346 correlation coefficient at ELK2 station. Here, the results are supported by the in-situ measurements to present the accuracy of the estimations. When the 6-day estimations are considered to figure out how the model fits the site observations, the best accuracy of the model is computed as 2.2 cm for the same station as well. Although the reflector height estimation has become a routine and well-known method, in this study the accurate estimation of vertical differences is examined to obtain precisions from the reflector heights. The absolute vertical differences as 10 cm and 20 cm are considered as the true value and RMSEs of vertical shifting amounts are computed. According to the results, the overall accuracy is obtained between 2.92 cm and 3.96 cm. However, this also shows that some of the reflector height estimations are insignificant. This situation brings a necessity to examine the differences as well. With the help of statistical considerations, more accurate and valid solutions in reflector height retrieving can be provided.