1. Introduction

Global navigation satellite system (GNSS) is the basic component of many kinematic or dynamic applications that require high-precision positioning such as unmanned aerial vehicles (^{Eling et al., 2015}), mobile mapping (^{Nocerino et al., 2017}), road surveying (^{Jo & Sunwoo, 2014}), marine positioning (^{Jiang et al., 2015}), structural health monitoring (^{Shen et al., 2019}) and autonomous vehicles (^{Kuutti et al., 2018}). GNSS positioning techniques vary according to the required accuracy for kinematic applications. In high-precision kinematic positioning studies, the post-process kinematic technique is generally preferred, and double-differential observations are used (^{Paziewski et al., 2018}). Post-process kinematic (PPK) technique has proven its reliability and effectiveness by providing centimeter level accuracy after the resolution of the carrier phase integer. But the accuracy of the PPK method may be adversely affected by the long baselines (^{Ocalan, 2016}). However, positioning accuracy is not affected by the baseline length in Precise Point Positioning (PPP) technique since the technique requires only one receiver (^{Furones et al., 2012}). PPP is a method that can generate positioning at the centimeter or decimeter level employing precise satellite orbit and clock data that can be obtained from analysis centers, such as International GNSS Service (IGS), Bundesamt für Kartographie und Geodäsie (BKG), Centre National d'Etudes Spatiales (CNES), European Space Agency (ESA), Deutsches GeoForschungsZentrum (GFZ) and GMV Aerospace and Defense (GMV)), with undifferenced code and phase measurements using a single GNSS receiver. Thus, it has become an essential alternative to PPK in evaluating kinematic GNSS data gathered with aircraft, vessels, and cars at high speed (^{Alkan et al., 2017}; ^{Elliott & Hegarty, 2017}; ^{Erol et al., 2020}; ^{Misra & Enge, 2011}). ^{El-Mowafy (2011)} compared PPP and PPK coordinate results using fixed-wing aircraft and showed that their differences ranged from a few millimeters to 1.5 decimeters. Moreover, the convergence time of the solution can be shortened, and the position accuracy can be increased by adding GLONASS observations to GPS observations in the PPP method (^{Choy et al., 2013}). In the near future, the PPP method is expected to be used effectively in smart city applications such as parking, cargo delivery, shared vehicle use, emergency response and autonomous driving (^{Brovelli et al., 2016}; ^{Robustelli & Pugliano, 2019}; ^{Xu et al., 2018}).

At present, GNSS receivers have become the main component of precise navigation systems with the high precision and accuracy that PPP and PPK methods offer. Still, it may not always be possible to use the position information of GNSS receivers since signal interruptions in areas with many restrictions on satellite visibility, such as footbridges, flyovers, tunnels, or close to tall buildings or forests. In these situations, the number of visible satellites (NVs) is insufficient; that's why desired positioning accuracy level may not be provided. Although multi-constellations increase satellite visibility and geometry, they cannot provide sufficient enhancement in positioning accuracy compared to the GPS-only results unless there is a weak number of GPS satellites and the poor satellite geometry (^{Bakuła et al., 2015}; ^{Li et al., 2019}; ^{Specht et al., 2020}, ^{Ocalan et al., 2016}). Also, multi-constellation solutions in challenging conditions may not be sufficient for high-precision positioning studies (^{Petovello, 2003}; ^{Yigit et al., 2014}). Therefore, satellite systems are often used in such areas by being integrated with inertial sensors due to their complementary properties. The inertial measurement unit (IMU) provides high-rate signals (specific force and angular velocity) for monitoring the ego-motion of the sensors. Integrating the measurements from the GNSS receiver with the measurements from the IMU is achieved with the Kalman filter. This conventional configuration can provide very high accuracy due to its completeness.

In this paper, to evaluate the positioning performance of the GNSS/IMU integration, a field experiment was carried out in two different environments, urban and wooded areas with poor GNSS satellite geometry and limited satellite visibility. In this contribution, there are three main objectives. Firstly, the positioning accuracies of the satellite-based and loosely-coupled based (LC-based) results were comparatively investigated. Second, in these conditions, the impact of satellite systems (including multi-GNSS and GPS-only) on positioning accuracy was examined. Finally, a comparative analysis of the accuracy performance of the PPP and PPK approaches in challenging situations was conducted.

2. Motivation

In the literature, several studies evaluated the loosely coupled integration of IMU with the RTK, PPK or PPP methods separately; however, few studies assess the loosely coupled integration of IMU with both PPK and PPP methods under challenging environments with limited satellite view. ^{Godha and Cannon (2007)} achieved an 80-90% improvement by adding the IMU system to the PPK method during GPS outages in an urban area. ^{Vu et al. (2013)} achieved a centimeter precision result by integrating the data collected with dual-frequency GPS processed according to the PPK method and 200 Hz IMU on a land vehicle. ^{Vana and Bisnath (2020)}, in which they integrated PPP/IMU with the land vehicle and obtained 40 cm accuracy in the horizontal component and 1.2 m in the vertical component during 30 seconds of signal interruption. The primary motivation of this study is to examine the performance of PPP and PPK methods as a result of IMU integration in the same environment and conditions.

In most of the PPP/PPK and IMU integration studies, the obtained positioning performance of the proposed methods has been compared to the other GNSS-based results named as reference data (^{Falco et al., 2012}; ^{Chiang et al., 2013}; ^{Falco et al., 2017}). However, these reference data are also highly affected by GNSS-based error sources such as clock-related errors, atmospheric errors, multipath errors, orbital errors, and receiver noise, especially in harsh environments such as urban areas, heavy tree cover etc. and thus may offer a low accuracy position information. As a result, comparing the proposed method with the result of another GNSS-based method may not be appropriate in such challenging environments. The highest grade IMUs are used in some studies to obtain the high accuracy reference solution, but this solution is not sufficient to get the exact trajectory (^{Ilci & Toth, 2020}; ^{Otegui et al., 2021}; ^{Zhang et al., 2020}). To avoid this situation, in this study, reference data were obtained by terrestrial methods, and high-accurate reference data were obtained along the trajectories in urban and wooded areas. In this study, besides the comparative analysis of the PPP-based and PPK-based solutions, the GPS-based and GNSS-based solutions and the LC-based and satellite-based solutions are also comparatively analyzed.

3. Loosely Coupled model

GNSS/INS integration methods are divided into three different types called "loose", "tight", and "ultra-tight" (^{Solimeno, 2007}; ^{Gao and Lachapelle, 2008}; ^{Petovello, 2003}). The fundamental difference between these methods is the type of data shared by the GNSS receiver and INS. In the LC technique, the positions, velocities, and times (PVT) estimated by the GNSS receiver are integrated with the INS solution, while in the case of a tightly-coupled method, measurements from GNSS raw measurements (i.e., pseudorange, carrier phase measurements and Doppler observables) and measurements from inertial sensors are processed to estimate PVT. The ultra-tight integration method includes the baseband signal processing of GNSS receivers (i.e., the digital tracking loops) (^{Falco et al., 2017}). For the integration of individual systems for the accuracy or integrity requirements, LC integrations should be preferred (^{Bhatti et al., 2007}). Even though many articles describe LC integrations for automotive applications in urban areas (^{Angrisano et al., 2012}; ^{Atia & Waslander, 2019}; ^{Godha & Cannon, 2007}; ^{Li et al., 2018}; L. ^{Zhao et al., 2016}; ^{S. Zhao et al., 2016}), limited studies have been conducted to evaluate the effectiveness of LC solutions based on different environments such as forestry and open skies from a practical point of view. However, the loosely coupled integration algorithm was used in this study, as ^{Salytcheva (2004)} also described, because tightly coupled algorithms have less computational efficiency and a more complex system and measurement model than loosely coupled schemas.

Kalman Filter is used in the LC technique in order to determine the position and velocity errors, gyroscope bias error, first-order Markov process random noise errors and accelerometer bias error (^{Hol, J. D. 2011}; ^{Xu et al., 2018}). Then, INS position error 6P, velocity error δP, velocity error δV, gyroscope bias errors εb, and first-order Markov process random noise errors of gyroscope εr and accelerometer bias error 𝝯 constitutes the state vector X_K= (δP_KδV_Kε_b,k𝝯_K)T. The state equation of GNSS/INS LC can be written as:

Where,

F _{K K} -1: the state transition matrix

G_K: the system noise distribution matrix

W_K: the system noise vector

The position and velocity differences between INS and GNSS can be regarded as measurements. The measurement model is written as:

Where,

N _g: the position error of GNSS

M _g: the velocity error of GNSS

H _p, H _v : state space transformation matrices

V _k : the measurement error is considered as white noise, i.e., E(V _k ) = 0. Its covariance R _k can be estimated as R _k = E(V _K V _K ^T ).

Z _k : the position and velocity difference between the GNSS measurements and INS estimation.

Under the normal cases, there is consistency between the position and velocity states of GNSS and that of INS, and for this reason, the position and velocity difference Z is small, equal to the sum of GNSS noise and INS errors, i.e., Z _k = V _k (^{Xu et al., 2018}). The item Z _k is GNSS noise when all INS errors are corrected. The velocity difference δV is optional in some LC integration systems (^{Falco et al., 2017}). The GNSS/INS integration system becomes integrated with position fusion, and the measurement model becomes Z _k = H _P,k X, + N_g, _k (^{Xu et al., 2018}). Details about the LC integration model can be found in (Hoi, J. D. 2011, ^{Qin et al., 2015}).

4. Study Area

In this study, the data were collected by using a GNSS receiver and an IMU sensor mounted on a three-wheel hand pushcart (carrier platform) in the Yildiz Technical University, Davutpasa Campus in 2018 (DoY: 137). The test environments are shown in Figure 1. The campus features medium-sized buildings that create lower elevation angles relative to dense urban areas, and trees on both sides mainly cover the roads. The test was conducted in two different areas; a wooded area where the GNSS signals are partly interrupted due to trees around it and an urban area where GNSS signals are heavily interrupted by the buildings and the footbridges between the buildings. The roads in the test environments are smooth and are not be exposed to high vibration-effect.

Figure 1 Study areas (blue line: wooded area; red line: urban area) 

5. Data Collection and Processing

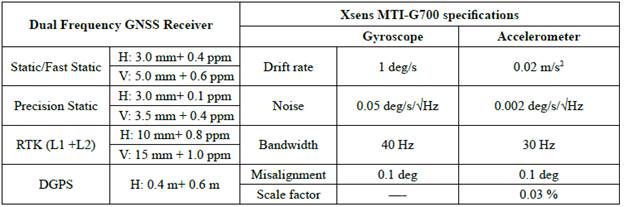
The data collection vehicle is shown in Figure 2. A Topcon HyperPro dual-frequency GNSS receiver and a high-precision Xsens MTi-G-700 IMU were used in this study. In addition, raw data were received and stored on a laptop. MTi-G-700 sensor generates the accelerometer and gyroscope data. The technical characteristics of the IMU and GNSS receiver are shown in Table 1. The data sampling rates of the GNSS and IMU was set to 10 Hz and 400 Hz, respectively. In two test environments, data were collected for approximately 1 hour. In the study, the 20-min duration is considered as convergence time. Therefore, 20 minutes of static observation data were collected before the vehicle started moving.

Figure 2 Data collection vehicle ( a) wooded-area; b) urban area) 

Table 1 Specifications of IMU and GNSS receiver 

Table 2 Solution groups 

All the processes were conducted using Inertial Explorer post-processing software developed by NovAtel. The collected GNSS data was processed using post-process kinematic (PPK) and Precise Point Positioning (PPP) techniques in both only GPS signals and GPS/GLONASS (GNSS) multi-constellation satellite system signals. The YLDZ base station (located on the roof of the Yildiz Technical University, Civil Engineering Faculty) data of the related test dates were used as the reference in the PPK processes. The maximum distances of the YLDZ base station to the wooded and urban areas are 280 m and 160 m, respectively. In GPS-only and GNSS processes in both PPK and PPP methodologies, the cut-off angle and data processing intervals were set to 10 degrees and 0.1 seconds, respectively. Then, these PPK and PPP solutions were separately combined with the 400 Hz IMU data using the LC algorithm. All these procedures were repeated for wooded and urban areas, and the results were exported in 10 Hz frequencies. So, eight different solutions were obtained: PPK/GPS, PPK/GNSS, PPP/GPS, PPP/GNSS, PPK/GPS-IMU, PPK/GNSS-IMU, PPP/GPS-IMU, and PPP/GNSS-IMU. For clarity, we grouped the solutions for the aimed comparisons seen in Table 2, and the solutions will be named as these groups. The reference solution for wooded and urban areas has been provided by the traditional surveying method, which is accurate to 1-2 centimetres by using a total station to determine the accuracy of the solutions. The obtained processing results were compared with that of reference coordinates.

6. Results

6.1. Wooded-Area Test:

Figure 3 depicts the satellite-based solutions in the wooded area. None of the epochs along the trajectory for these four solutions is missing. According to the findings, the satellite-based solutions are quite near to the reference trajectory through the route.

Figure 3 Trajectories of satellite-based solutions and the reference trajectory in the wooded-area 

Figure 4 shows the LC-based solutions in the wooded area. It can be observed that LC-based systems offer extremely accurate results that are comparable to satellite-based results.

Figure 4 Obtained trajectories of LC-based solutions and the reference trajectory in the wooded-area 

Figure 5 shows the 2D position errors of the satellite-based (top) and LC-based (middle) solutions and the NVs (bottom) during the observations. The satellite-based (top) and LC-based (middle) solutions provide lower than 22-cm error levels through the trajectory where the NVs is mostly higher than 10.

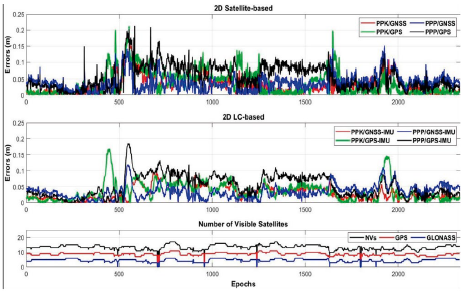
Figure 5 2D position errors in wooded-area (top: satellite-based; middle: LC-based), and the NVs during the wooded-area test (bottom) 

Figure 6 shows the height errors of the satellite-based (top) and LC-based solutions (middle) and the NVs (bottom) during the observations. Unlike the 2D position errors, LC-based height solutions provide better results than satellite-based height results. Also, both Figure 5 and Figure 6 show that the LC-based result's fluctuation is smaller than that of satellite-based results. Since Kalman filtering technique is used to determine the unknowns, thus, it can be concluded that the LC-based solutions are more reliable than the satellite-based solutions.

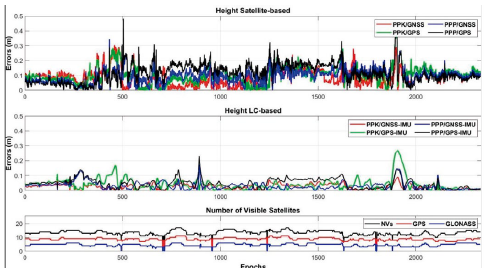
Figure 6 Height errors in wooded-area (top: satellite-based; middle: LC-based), and the NVs during the wooded-area test (bottom) 

Table 3 Error statistics of 2D position for wooded-area 

Table 3 gives the error statistics of the 2D position for satellite-based and LC-based solutions in the wooded area. In 2D position, satellite-based PPK/ GPS, PPK/GNSS, PPP/GPS, and PPP/GNSS solutions provide 0.21, 0.20, 0.21, and 0.16 meter errors in maximum and 0.04, 0.03, 0.06 and 0.04 meter errors on average, respectively. RMSE values of PPK and PPP methods reveal that the GNSS-based solutions slightly improve positioning accuracy compared to the GPS-based methods.

LC-based PPK/GPS-IMU, PPK/GNSS-IMU, PPP/GPS-IMU, and PPP/GNSS-IMU position solutions provide 0.17, 0.10, 0.18, and 0.12 meter errors in maximum and 0.04, 0.03, 0.05 and 0.03-meters errors on average, respectively. Comparing the satellite-based and LC-based solutions reveals that LC integration provides a remarkable improvement only in the maximum errors. In contrast, average and RMSE values of LC-based methods provide a very slight improvement.

Table 4 Error statistics of height for wooded-area 

The error statistics of the height component for satellite-based and LC-based solutions are given in Table 4. Height errors of satellite-based PPK/GPS, PPK/GNSS, PPP/GPS, and PPP/GNSS solutions provide 0.41, 0.30, 0.48, and 0.43 meters in maximum and 0.10, 0.08, 0.12 and 0.10 meters on average, respectively. Comparing the satellite-based PPK and PPP methods reveals that the PPK-based errors in maximum, average, and RMSE statistics are less than PPP-based errors. The comparison of the GPS and GNSS solutions reveals that the GNSS solutions are better than that of GPS solutions.

LC-based PPK/GPS-IMU, PPK/GNSS-IMU, PPP/GPS-IMU, and PPP/GNSS-IMU solutions of height component provide 0.27, 0.09, 0.23, and 0.17 meters in maximum and 0.04, 0.02, 0.05 and 0.03 meters errors on average, respectively. The maximum errors of all LC-height solutions are in the 1-2 dm level. Comparing the satellite-based and LC-based results in the height component reveals that LC integration significantly improves PPK/GPS, PPK/GNSS, PPP/GPS and PPP/GNSS maximum, average RMSE statistics.

6.2. Urban-Area Test:

Figure 7 shows the satellite-based solutions in the urban area. This trajectory has five bridges for pedestrians from building to building that causes satellite signal blockage. Under or nearby these bridges, satellite-based four solutions either do not give any results or give very erroneous results. PPK/GNSS, PPK/GPS, PPP/GNSS, and PPP/GPS solutions have 22%, 36%, 25% and 31% missing gaps, respectively, through the trajectory. Although GNSS-based methods provide fewer gaps than GPS-based methods, the produced solutions of the GNSS-based methods are mostly unsatisfactory under or nearby the bridges like GPS-based methods. Moreover, PPP/GNSS and PPP/ GPS trajectories dramatically leave the reference trajectory in some route parts.

Figure 7 Trajectories of satellite-based solutions in the urban-area 

Figure 8 shows the LC-based solutions in the urban area. There are no missing epochs in all LC-based solutions. GNSS/IMU integrated LC-based solutions bridge the gaps of the satellite-based solutions in all these methodologies, providing continuous trajectories. Although PPP-based methods provide uninterrupted solutions, they are significantly separated from the reference route in some regions along the course.

Figure 8 Trajectories of LC-based solutions in the urban-area 

Figure 9 shows the 2D position errors of the satellite-based (top) and LC-based integrated solutions (middle) and the NVs during the observations (bottom). The negative effect of the five bridges is seen as the five gaps in this figure, and the error values reach the highest values near these epochs. Also, it can be seen that the maximum errors obtained from these processes occur before and after these gaps. Figure 9 also visualize that the maximum errors of PPP-based solutions reach up to 3 meters between the 1500 to 2000 epochs. The middle part of this figure indicates that the GNSS/IMU integrated LC-based solutions bridge the GNSS solution's gaps in all four methods. But, especially PPP-based solutions can not provide satisfactory improvement in some parts of the trajectory.

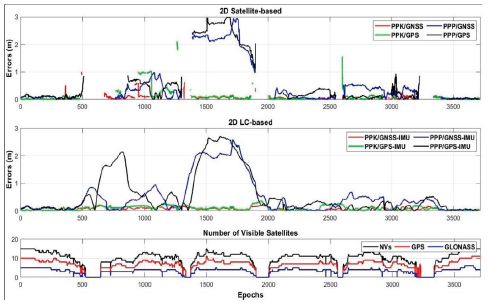
Figure 9 2D position errors in urban-area (top: satellite-based; middle: LC-based) and the NVs during the observations (bottom) 

Figure 10 gives the height errors of the satellite-based (top) and LC-based (middle) solutions and the NVs during the observations (bottom). Similar to the 2D position errors, five gaps are seen in the height component in the top part of the figure. All method's errors reach meter-level, but PPK-based solutions are better than PPP-based ones. The middle part of the figure shows that the IMU integration fills the gaps in all methods and improves height accuracy.

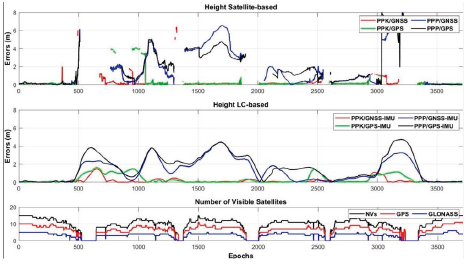
Figure 10 Height errors in urban-area (top: satellite-based; middle: LC-based) and the NVs during the observations (bottom) 

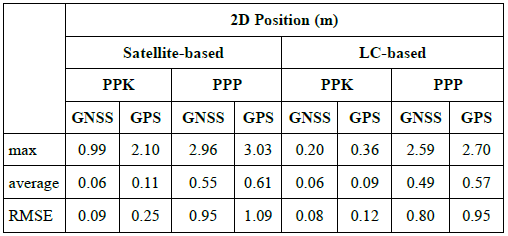
Table 5 gives the error statistics of the 2D position for satellite-based and LC-based solutions in the urban area. The satellite-based PPK/GPS, PPK/GNSS, PPP/GPS, and PPP/GNSS solution errors are 2.10, 0.99, 3.03, and 2.96 meters in maximum and 0.11, 0.06, 0.61 and 0.55 meters on average, respectively. The satellite-based PPK methods outperform the PPP methods in maximum, average, and RMSE statistics in the GNSS challenging environment. GNSS-based methods are significantly better than GPS-based solutions in PPK-based solutions, while in the PPP-based solutions, this improvement is very slight.

Table 5 Error statistics of 2D position for urban-area 

LC-based PPK/GPS-IMU, PPK/GNSS-IMU, PPP/GPS-IMU, and PPP/GNSS-IMU solutions provide 0.36, 0.20, 2.70, and 2.59 meters in maximum and 0.09, 0.06, 0.57 and 0.49-meter errors on average, respectively. Similar to the satellite-based solutions, the provided accuracies of the PPK-based methods are significantly better than that of PPP-based methods in the LC-based solutions, and GNSS-based methods better perform than the GPS-based methods. Although the LC-based methods can not improve the average values substantially compared to the satellite-based methods, LC-based methods fill the gaps through the trajectory (nearly %30 of the trajectory), provide lower maximum errors, and less fluctuation in the error values.

The error statistics of the height component for satellite-based and LC-based solutions are given in Table 6. Height errors of satellite-based PPK/GPS,PPK/GNSS, PPP/GPS, and PPP/GNSS solutions are 10.86, 6.43, 12.95 and 8.73 meters in maximum, and 0.38, 0.24, 1.90 and 1.75 meters on average, respectively. These results reveal that the PPK methods provide a better solution than PPP methods in the height component in the urban area and the GNSS-based methods outperform the GPS-based methods.

Table 6 Error statistics of height for urban-area 

Height errors of LC-based PPK/GPS, PPK/GNSS, PPP/GPS, and PPP/ GNSS solutions are 1.64, 1.49, 4.74 and 4.45 meters in maximum, and 0.34, 0.16, 1.67 and 1.31 meters on average, respectively. Similar to the satellite-based methods, LC-based results reveal that the PPK-based and GNSS-based methods provide better than PPP-based and GPS-based solutions, respectively.

The LC-based solutions enhance the maximum height accuracies for all methods. The average results of GNSS-based solutions (PPK-GNSS and PPP-GNSS) indicate that LC-based solutions slightly improve height accuracy. However, on GPS-based solutions (PPK-GPS and PPP-GPS methods), LC slightly deteriorates the height accuracies.

7. Conclusions

GNSS has been the playmaker of positioning applications for the last two decades, from low-cost single-frequency receivers to state-of-the-art technologies. Nevertheless, this technology needs another assistance technology, such as IMU, in some conditions where obstacles partially or entirely block the GNSS signals. This study aims to determine the positioning performance of the GNSS/IMU integrated solution in the two GNSS signal blockage test environments; a wooded area and an urban area. Using the obtained results, this study tests and analyses three comparisons, namely satellite-based and LC-based solutions, GNSS-based and GPS-based solutions, and PPK-based and PPP-based solutions.

In the wooded area test, similar to the LC-based methods, the satellite-based methods provided cm-level accuracies through the trajectory due to the higher NVs. LC-based methods slightly improved the accuracy, reduced the fluctuation in the errors, and offered more reliable solutions than the satellite-based method. Moreover, it can be concluded that the GNSS-based methods offered a slightly better solution than GPS-based methods and PPK-based methods provided a slight improvement over the PPP-based methods.

In the urban area test, the satellite-based methods have very big gaps in the solutions. LC-based solutions filled the gaps, provided uninterrupted solutions with a slight positioning improvement, lower fluctuations in the errors and provided more reliable solutions than the satellite-based results. Moreover, PPK-based solutions provided significant progress compared to the PPP-based methods and GNSS-based methods outperformed the GPS-based solutions.

Considering the abovementioned results, it can be concluded that the GNSS/IMU integration with PPK methods provides a reliable and uninterrupted solution with the best positioning performance in both the highly and partially GNSS-denied environments.