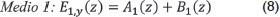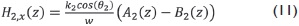Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Entramado
Print version ISSN 1900-3803
Entramado vol.12 no.2 Cali July/Dec. 2016
https://doi.org/10.18041/entramado.2016v12n2.24222
http://dx.doi.org/10.18041/entramado.2016v12n2.24222
La mitocondria como un sistema de multicapas ópticas para la propagación de los campos electromagnéticos
Mitochondria as a multilayer optical system for propagating electromagnetic fields
As mitocôndrias, como um sistema óptico de múltiplas camadas para a propagação de campos electromagnéticos
Francis Armando Segovia-Chaves*, Daniel Suescún-Díaz** Diego Alejandro Rasero-Causil***
* Doctor(c) en Ciencias Físicas, Universidad Nacional de Colombia. Profesor de planta Universidad Surcolombiana, Neiva-Huila, Colombia. fasegoviac@unal.edu.co, francis.segoviac@gmail.com.
** Ph. D en Ciencias Físicas, Universidade Federal Do Rio De Janeiro. Profesor de planta Universidad Surcolombiana, Neiva-Huila, Colombia. dasuescun@javerianacali.edu.co.
*** Doctor(c) en Ciencias Físicas, Universidad de Sucre, Colombia. Docente tiempo completo Universidad Surcolombiana, Neiva-Huila, Colombia. diegorosero@gmail.com.
Este es un artículo Open Access bajo la licencia BY-NC-SA (http://creativecommons.org/licenses/by-nc-sa/4.0/)
Cómo citar este artículo: SEGOVIA-CHAVES, Francis Armando, SUESCUN-DIAZ, Daniel; RASERO-CAUSIL, Diego Alejandro. La mitocondria como un sistema de multicapas ópticas para la propagación de los campos electromagnéticos. En: Entramado. Julio - Diciembre, 2016 vol. 12, no. 2, p. 246-253 http://dx.doi.org/10.18041/entramado.2016v12n2.24222.
Recibido: 25/06/2015 Aceptado: 10/11/2015
Resumen
El artículo propone estudiar la propagación de los campos electromagnéticos a través de la mitocondria. Se presenta un modelo simplificado de la mitocondria como un sistema periódico de multicapas de índices de refracción alternantes. Mediante el método de transferencia matricial se calcula la dependencia, la reflectancia y transmitancia en función de la longitud de onda del campo electromagnético incidente. Se observa la existencia de una región de longitudes de onda (o frecuencia prohibidas) en la cual no existe propagación de los campos a través del sistema, esto corresponde a una reflectancia máxima R=1.
Palabras clave: Campos electromagnéticos, índice de refracción, longitud de onda, mitocondria, reflectancia, transmitancia.
Abstract
The article aims to study the propagation of electromagnetic fields through the mitochondria. We present a simplified model of the mitochondrion as a periodic multilayer of alternating refractive indices. Using the transfer matrix method calculates dependence reflectance and transmittance versus wavelength of incident electromagnetic field. Observe the existence of a wavelength region (or prohibited frequency) in which there is no spread of the fields through the system, this corresponds to a maximum reflectance R = 1.
Keywords: Electromagnetic fields, refractive index, wavelength, mitochondria, reflectance, transmittance.
Resumo
O artigo tem como objetivo estudar a propagação de campos eletromagnéticos através das mitocôndrias. Nós apresentamos um modelo simplificado da mitocôndria como uma multicamada periódica de alternância de índices de refração. Utilizando o método de matriz de transferência calcula reflectância dependência e transmitância contra o comprimento de onda de campo eletromagnético incidente. Note-se a existência de uma região de comprimento de onda (ou frequência proibida) em que não há nenhuma propagação dos campos através do sistema, isto corresponde a um máximo de reflectância R = 1.
Palavras-chave: Campos electromagnéticos, índice de refração, comprimento de onda, as mitocôndrias, reflectância, transmitância.
Introducción
Se inicia este trabajo con una breve fundamentación de conceptos referentes a la mitocondria, para luego proponer el modelo físico matemático que representará el sistema óptico.
Es conocido que las células, además de constituir las unidades básicas del cuerpo humano, son las que intervienen en todas las actividades requeridas por el organismo para su supervivencia. El componente vivo de la célula es el proto-plasma, que se subdivide en citoplasma y nucleoplasma. Existen más de 200 tipos celulares diferentes, la mayoría de las células tienen características comunes que les permiten cumplir con sus diversas funciones (Gartner, 2003). Ahora bien, en las células se encuentran presentes las mitocondrias. Las mitocondrias se conocen desde hace más de un siglo, el primer investigador en describir estas estructuras fue el patólogo e histólogo alemán Richard Altman; las identificó como responsables de ciertas funciones vitales y eran estructuras intracelulares (vivían dentro de las células) a las que llamó mioblastos. Benda utilizó la denominación mitocondrias, del griego mitos que significa hilo y condos gránulo (Martorell, 2014). Estas estructuras intracelulares son organelos presentes en prácticamente todas las células eucariotas (Arboleda, 2008). La organización interna de células eucarióticas está caracterizada por los compartimientos de diversos organelos (núcleo, retículo endoplasmático, mitocondria, microsomas) los cuales se relacionan para funciones específicas fisiológicas. Estos compartimientos son generalmente encerrados por una o dos membranas que consisten de una bicapa lípida. Las mitocondrias están conformadas por dos membranas, una externa y una interna. El compartimiento entre ambas se denomina espacio inter-membrana. La membrana interna presenta plegamentos que forman crestas, y encierra un espacio lleno de un líquido viscoso, denominado espacio de la matriz. La matriz mitocondrial contiene el ADN mitocondrial, mitoribosomas y RNA mitocondrial. En su interior se llevan a cabo reacciones de vital importancia como el ciclo de Krebs y beta-oxidación de ácidos grasos (Guevara, 2012).
La mitocondria presenta distintas morfologías, su número varía por célula dependiendo de los requerimientos de energía de la misma célula, siendo los tejidos más ricos en mitocondrias el del músculo cardíaco, el músculo esquelético y el cerebro. Las primeras imágenes sobre su estructura aparecieron en los años cincuenta, con el uso del microscopio electrónico, el cual a diferencia del microscopio convencional utiliza electrones. Se inicia el camino por el biólogo rumano George Palade y el físico e histólogo sueco Fritiof Sjöstrand, quienes observaron distintos elementos estructurales de estos orgánulos como la membrana externa, la membrana interna y las crestas mitocondriales (Martorell, 2014). Sumada a las observaciones realizadas con el microscopio electrónico donde se muestra la mitocondria como organelos ovoides de alrededor 0,5μm de diámetro, las pruebas de fluorescencia muestran que las mitocondrias tienen filamentos. Un solo filamento de mitocondria tiene alrededor de un diámetro de 100-500nm y una longitud de alrededor 10μm, ellas están asociadas con microtúbulos en el citoesqueleto.
Desde un punto de vista físico, una propiedad importante para la propagación de la luz dentro de un medio es el índice de refracción n (Reitz, 1986). Las células vivas se pueden observar con nitidez en un microscopio de contraste de fases o de contraste de fases interferencial (Kierszenbaum, 2012). Cuando la luz pasa a través de una célula viva, la fase de la onda luminosa varía en relación con el índice de refracción de la célula: al pasar la luz en una región relativamente gruesa o densa de la célula (el núcleo), esta se retrasa y su fase queda desplazada con respecto a la de la luz que ha pasado a través de una región adyacente de citoplasma, más fina. Tanto los microscopios de contraste de fases y de contraste de fases interferencial aprovechan los efectos de interferencia que se producen, cuando se combinan estos dos grupos de ondas, se origina una imagen de la estructura celular. Estas técnicas permiten realizar mediciones de los índices de refracción para diferentes componentes intra-celulares. Los filamentos de mitocondria que aparecen en imágenes de microscopía electrónica al realizar un corte transversal, muestran una serie de capas alternadas de matriz y espacio intermembrana, con una distancia d≈100nm (Cifra, 2010). En la Figura 1 se representa un modelo simplificado de la mitocondria.
Con el modelo representado por la Figura 1, se está en condiciones en proponer un modelo físico matemático que permita construir de manera simplificada, la mitocondria como un sistema de medios alternados. Este trabajo se encuentra dividido en tres partes: Primero, se realiza el planteamiento del problema, se presentan además los trabajos más sobresalientes con respecto a la propagación de los campos electromagnéticos en medios periódicos. Segundo, se muestran las relaciones físicas más importantes y se describe en esencia el método de la matriz de transferencia (MMT) el cual permite determinar los flujos de energía reflejada (reflectancia) y transmitida (transmitancia). Por último se presentan los resultados obtenidos.
1. Descripción del problema
A partir de la Figura 1 se presenta un modelo óptico unidimensional de una mitocondria ideal, como se muestra en la Figura 2. Tal sistema se comporta como un medio periódico donde la luz puede propagarse.
Para estudiar el modelo propuesto en la Figura 2, se considera la incidencia de una onda electromagnética (campo electromagnético) plana monocromática, desde un medio caracterizado por un índice de refracción ni y con un ángulo de incidencia θ. El medio de salida de la onda electromagnética tiene un índice de refracción ns. El sistema está formado por N bicapas de medios alternados no dispersivos, con índices de refracción n1 y n2 , cada uno de ellos tiene un espesor l1 y l2.
Se debe tener presente que la propagación de los campos electromagnéticos a través del modelo propuesto en la Figura 2, ha tenido una extensa investigación en la física aplicada, en telecomunicaciones, electrónica y demás campos de la ingeniería y la ciencia. El conocer el comportamiento de los campos electromagnéticos al pasar a través de un material brinda información importante para su caracterización y posterior uso, así como el descubrimiento de nuevos fenómenos aprovechables. Una multicapa está hecha de la combinación de dos o más medios materiales diferentes. Por ejemplo se ha reportado la fabricación de espejos a base de multicapas con distribución tipo chirped (Agarwal, 2006) y Gaussian (Estévez, 2009) en sus índices de refracción. Tambien se ha explorado el diseño de reflectores usando serie de Fibbonacci (Grushina, 2009) y algoritmos genéticos (Jiang, 2008). El estudio de la propagación de ondas en medios periódicos se remonta a los trabajos de Lord Rayleigh (Rayleigh, 1892) y en el libro de León Brillouin (Brillouin, 2003). Este tipo de periodicidad marca el nacimiento de los cristales fotónicos, de manera independiente sus descubridores son Eli Yablanovitch (Yablanovitch, 1987) y Sajeev Jhon (Sajeev, 1991). Los cristales fotónicos son una nueva especie de semiconductores de luz, en ellos la luz siempre encuentra alguna dirección por la que pueden propagarse a través del cristal y se hace referencia al gap fotónico, como el rango de frecuencias prohibidas donde no existe propagación de la luz (Joannopoulos, 2011). Este tipo de estructuras se caracterizan por presentar modulación periódica en el espacio de su constante dieléctrica (o índice de refracción) (Soukoulis, 2002). En esa misma línea, Johnson y colaboradores (Johnson, 1985), consideran la propagación de plasmones superficiales en una multicapa periódica finita conformada por medios dieléctricos intercalados de espesor constante. Al solucionar la ecuación de Laplace, numéricamente determinan la relación de dispersión aplicable a la elección arbitraria de los parámetros del medio y el número de periodos. Siguiendo los lineamientos descritos en el trabajo de Johnson, se demuestra que cuando una luz se propaga en un medio periódico dieléctrico con inhomogeneidades, se encuentra sujeta a múltiples dispersiones; lo cual conduce a la aparición de las estructuras de banda y a la dependencia de la transmitancia con el espesor de los medios (McCall, 2001). Variaciones del modelo de un sistema periódico de multicapas plano encuentra una extensión al considerar que los medios constituyentes son dieléctricos y metales, y la de radiación electromagnética incide de forma normal al sistema. Para ello, haciendo uso de una buena aproximación clásica para el caso óptico se describe la dependencia con la frecuencia de las propiedades eléctricas a partir del modelo fenomenológico de Drude Sommerfeld (Sukhoivanov, 2009).
2. Metodología propuesta
Para resolver el sistema descrito por la Figura 2 se empleó el conocido método de la matriz transferencia (MMT) y así se pudo estudiar la propagación de los campos electromagnéticos en la mitocondria. A continuación se describe el MMT con el cual se determinan los rangos de longitudes de onda para los cuales existe una reflectancia R y transmitancia T, en la estructura mitocondrial simplificada.
Método de la matriz transferencia
Las ecuaciones fundamentales de la electrodinámica vienen determinadas por los dos pares de ecuaciones de Maxwell en forma diferencial, (Hecht, 2002):
Donde los vectores de campo electromagnético vienen determinados por:  El vector de campo eléctrico,
El vector de campo eléctrico,  el vector de desplazamiento eléctrico,
el vector de desplazamiento eléctrico,  y
y  representan los vectores de inducción y de campo magnético, respectivamente. Las fuentes de los campos electromagnéticos están determinados por la densidad volumétrica de carga eléctrica p y el vector de densidad de corriente eléctrica
representan los vectores de inducción y de campo magnético, respectivamente. Las fuentes de los campos electromagnéticos están determinados por la densidad volumétrica de carga eléctrica p y el vector de densidad de corriente eléctrica  . En la Ecuación 1, tenemos las leyes de Faraday y de Gauss. La primera implica que variaciones temporales del campo magnético son fuentes de campo eléctrico y la segunda, densidades volumétricas de carga eléctrica son fuentes o sumideros del vector de campo eléctrico. En la Ecuación 2 presentamos la ley de Ampere-Maxwell, el campo magnético es originado por las densidades de corriente eléctrica y de desplazamiento eléctrico. Y por último, la ecuación para la no existencia de monopolos magnéticos (Greiner, 2012). Las ecuaciones de Maxwell necesariamente se deben complementar con las ecuaciones constitutivas o relaciones materiales: para medios lineales, homogéneos e isótropos tenemos (Callister, 2007):
. En la Ecuación 1, tenemos las leyes de Faraday y de Gauss. La primera implica que variaciones temporales del campo magnético son fuentes de campo eléctrico y la segunda, densidades volumétricas de carga eléctrica son fuentes o sumideros del vector de campo eléctrico. En la Ecuación 2 presentamos la ley de Ampere-Maxwell, el campo magnético es originado por las densidades de corriente eléctrica y de desplazamiento eléctrico. Y por último, la ecuación para la no existencia de monopolos magnéticos (Greiner, 2012). Las ecuaciones de Maxwell necesariamente se deben complementar con las ecuaciones constitutivas o relaciones materiales: para medios lineales, homogéneos e isótropos tenemos (Callister, 2007):
En la Ecuación 3, ∈ y μ son la permitividad dieléctrica y permeabilidad magnética, respectivamente.
Interesa estudiar la propagación de la onda electromagnética sin considerar sus fuentes, es decir,  . La ecuación que rige la propagación de la onda electromagnética es una ecuación diferencial de segundo orden de la forma (Soto, 2009):
. La ecuación que rige la propagación de la onda electromagnética es una ecuación diferencial de segundo orden de la forma (Soto, 2009):
Las soluciones de interés de la Ecuación 4, son las ondas planas monocromáticas,
Donde  representa el vector de onda y w es la frecuencia angular de los campos electromagnéticos. Las amplitudes E0 y H0 son constantes y en general son números complejos. Para el caso descrito en la Figura 2, la onda electromagnética incide sobre la interface haciendo un ángulo θi con respecto a la normal. Por lo tanto, es posible descomponer la onda con respecto al plano de incidencia XZ en una componente perpendicular (polarización s) y en una componente paralela (polarización p). En lo que sigue a lo largo de este trabajo solo estudiaremos la polarización s.
representa el vector de onda y w es la frecuencia angular de los campos electromagnéticos. Las amplitudes E0 y H0 son constantes y en general son números complejos. Para el caso descrito en la Figura 2, la onda electromagnética incide sobre la interface haciendo un ángulo θi con respecto a la normal. Por lo tanto, es posible descomponer la onda con respecto al plano de incidencia XZ en una componente perpendicular (polarización s) y en una componente paralela (polarización p). En lo que sigue a lo largo de este trabajo solo estudiaremos la polarización s.
El vector de onda incidente tiene por componentes en X y Z:
En la Ecuación 6, el módulo del vector de onda es  siendo c la velocidad de la luz en el vacío. Los medios que conforman el sistema periódico (Figura 2) son homogéneos en X, por lo tanto los índices de refracción no varían en esa dirección. A medida que la onda electromagnética se propaga experimenta múltiples reflexiones en cada una de las interfaces. En este caso, el campo eléctrico está constituido por la onda que viaja a la derecha (+Z) y otra a la izquierda (-Z), (Kavokin, 2007):
siendo c la velocidad de la luz en el vacío. Los medios que conforman el sistema periódico (Figura 2) son homogéneos en X, por lo tanto los índices de refracción no varían en esa dirección. A medida que la onda electromagnética se propaga experimenta múltiples reflexiones en cada una de las interfaces. En este caso, el campo eléctrico está constituido por la onda que viaja a la derecha (+Z) y otra a la izquierda (-Z), (Kavokin, 2007):
En la Ecuación 7, el subíndice j representa el medio en el que la onda se propaga, para nuestro caso j=1,2. La letra d hace referencia a la onda que viaja a la derecha +Z y la letra i la onda que viaja a la izquierda, -Z. En la Ecuación 7, los dos tipos de ondas (izquierda y derecha) las representamos por A(z) y B(z). Según lo anterior, el módulo del campo eléctrico en cada uno de los medios se escribe (Chuang, 1995):
Al reemplazar la Ecuación 5 en la ley de Faraday y al tener en cuenta las componentes del vector de onda dado por la Ecuación 6, obtenemos el vector de campo magnético en cada medio, el resultado es:
En las Ecuaciones 10 y 11, k1 y k2 representan los módulos del vector de onda en el medio 1 y 2 respectivamente. El propósito ahora es determinar las funciones A(z) y B(z) que aparecen en las soluciones del campo eléctrico y magnético. Para ello se deben imponer las condiciones de frontera de continuidad de la componente tangencial de los campos (Grant, 2013). En nuestro caso particular, el campo eléctrico es continuo en Y y el campo magnético es continuo en X, al realizar el procedimiento algebraico se obtiene un sistema de ecuaciones algebraicas que se condensan de la siguiente forma (Cottam, 2004):
Donde se ha definido (Lipson, 2010):
como la matriz dinámica para la polarización s. A medida que la onda electromagnética se propaga, debe atravesar diferentes fronteras de división. Por ello es necesario definir la matriz de transmisión entre los medios:
Además, existe un cambio de fase a lo largo de la dirección Z,
El anterior parámetro representado por la Ecuación 15, es positivo para ondas que se propagan a la derecha y negativo si se propagan a la izquierda, dj representa el espesor de los medios que se está considerando. Matricialmente definimos la matriz de propagación como Zhan (2013).
El mecanismo de propagación y transmisión ocurre a lo largo de todo el sistema. En general la matriz característica del sistema de la Figura 2, viene dada por Cabrera (1993)
Donde N representa el periodo de las bicapas que se consideran en el sistema. Al conocer la matriz característica, es posible obtener la reflectancia R y transmitancia T las cuales representan el flujo de energías reflejadas y transmitidas a medida que la onda electromagnética incide. Estas cantidades se determinan por las siguientes ecuaciones:
En las Ecuaciones 18 y 19, M11 y M21 representan los elementos matriciales de la matriz característica dada por la Ecuación 17.
En la siguiente sección, se presentan los flujos de energía reflejados (reflectancia) y transmitidos (transmitancia) considerando como caso particular parámetros de la mitocondria reportados en la literatura científica (Thar, 2004). Las simulaciones se realizan con el software Mathematica (Wolfram, 2009).
3. Resultados y discusión
Teniendo en cuenta el sistema descrito por la Figura 2, se estima que el medio de entrada y el de salida son iguales, para el caso de interés será el índice de refracción del citoplasma ni = ns = 1,35. Los índices de refracción para los medios que conforman la membrana son: medio 1 (matriz y membrana interna) n1 = 1.5 con espesor l1 = 50nm, medio 2 (espacio intermembrana) n2 = 1.35 con espesor l2 = 50nm, (Spencer, 1982). Se asume además que el número de bicapas viene determinado por N. En la Figura 3, se calculan los espectros de reflectancia R y transmitancia T. El índice de refracción de mitocondria es más alto que el citoplasma que lo rodea, lo cual hace que el retículo mitocondrial pueda actuar como una guía de onda óptica, es decir, la onda electromagnética se propaga en un medio periódico. Para longitudes de onda superiores a 400nm, todo el campo electromagnético incidente logra atravesar el sistema ya que el flujo de energía dado por la transmitancia es máxima (T≈1), esto se observa por la curva punteada. Caso contrario ocurre con la reflectancia (curva continua), donde para ese mismo rango de longitudes de onda, R≈0.
Sin embargo, al aumentar el número de bicapas como el que se presenta en la Figura 4, la región de máxima transmitancia (T≈1) se encuentra para longitudes de onda entre 300-800nm y la región de máxima reflectancia (R≈1) ocurre entre longitudes de onda de 270-290nm. El hecho que la reflectancia sea máxima, implica que la incidencia del campo electromagnético sobre la mitocondria en ese intervalo de longitudes de onda, supone la existencia de una región de frecuencias prohibidas (o gap). Ningún modo electromagnético puede propagarse a través de la mitocondria con un valor determinado de frecuencia que se encuentre en la región donde la reflectancia es máxima. Por fuera de los intervalos de longitudes de onda anteriormente señalados, existe una transmisión de la energía del campo electromagnético a lo largo del sistema biológico.
De los resultados presentados en las Figuras 3 y 4, se evidencia que el número de picos de transmisión para el sistema formado con un periodo de 50 bicapas es mayor que el número de picos de transmisión con un periodo de 20 bicapas. Es decir, existe una dependencia de los picos de transmisión con el número de periodos que conforman la mitocondria. Es de anotar que entre mayor sea el número de bicapas, las oscilaciones presentes en las curvas de reflectancia (o transmitancia) disminuyen.
En los dos anteriores casos, la incidencia de los campos electromagnéticos es normal. En general, existe una dependencia de las relaciones energéticas (reflectancia y transmitancia) tanto del número de bicapas N y del ángulo de incidencia θ . Esto se observa en la Figura 5, en esta se representa la curva de reflectancia con un número de bicapas N=50 y con el ángulo de incidencia del campo electromagnético sobre la mitocondria de θ=15° . A diferencia del resultado obtenido en la Figura 4, en la reflectancia existe un corrimiento en los valores a longitudes de onda menores (aproximadamente 270-285nm) para obtener una reflectancia máxima.
Ese corrimiento a longitudes de onda menores aumenta a medida que crece el ángulo de incidencia, como se muestra en la Figura 6; para valores comprendidos de la longitud de onda entre 200-225nm, la reflectancia es máxima. La mitocondria refleja todo el campo electromagnético que incida con ese rango de longitudes de onda y no logra el campo propagarse en el sistema.
4. Conclusiones
Los sistemas periódicos conformados por medios de índices de refracción diferentes, presentan ciertos rangos de longitudes de onda (o frecuencias) donde se permite y prohíbe la propagación de la radiación electromagnética. La mitocondria no es la excepción, se logró implementar analíticamente el método de la matriz de transferencia para el caso en que consideramos este sistema biológico como un sistema ideal de multicapas unidimensionales periódicas. Se presenta la dependencia de las curvas de reflectancia y transmitancia con el número de bicapas y del ángulo de incidencia, evidenciando que la mitocondria al igual que un | sistema periódico unidimensional de bicapas, presenta reregiones de frecuencias prohibidas (gap) donde la reflectancia R es máxima y por lo tanto no existe propagación del campo electromagnética en ese intervalo de frecuencias (o longitudes de onda).
Agradecimientos
A la Universidad Surcolombiana por su apoyo financiero, mediante el proyecto de investigación: Masas y mezclas de los neutrinos a partir de operadores autoadjuntos positivos asociados a espacios de Hilbert.
Conflicto de intereses
Los autores declaran no tener ningún conflicto de intereses.
Referencias bibliográficas
1. AGARWAL, Bhagwan D.; BROUTMAN, Lawrence J.; CHANDRAS-HEKHARA, K. In: Analysis and performance of fiber composites. John Wiley & Sons, 2006. [ Links ]
2. ARBOLEDA, Gonzalo; SÁNCHEZ, Ruth Mélida. Mitocondria y muerte celular. En: NOVA Publicación en Ciencias Biomédicas, 2008, vol. 6, no 10, p. 190-200. [ Links ]
3. BRILLOUIN, Leon. In: Wave propagation in periodic structures: electric filters and crystal lattices. Courier Corporation, 2003. [ Links ]
4. CALLISTER, William D.; RETHWISCH, David G. In: Materials science and engineering: an introduction. New York: Wiley, 2007. [ Links ]
5. CABRERA, José Manuel; LÓPEZ, Fernando Jesús; LÓPEZ, Fernando Agulló. En: Óptica electromagnética: Fundamentos. Addison-Wesley Iberoamericana España, 1993. [ Links ]
6. CIFRA, Michal, et al. Electric field generated by axial longitudinal vibration modes of microtubule. In: BioSystems, 2010, vol. 100, no 2, p. 122-131. [ Links ]
7. COTTAM, Michael G.; TILLEY, David R. In: Introduction to surface and superlattice excitations. CRC Press, 2004. [ Links ]
8. CHUANG, Shun Lien; CHUANG, Shun L. In: Physics of optoelectronic devices. 1995. [ Links ]
9. ESTEVEZ, J. O., et al. Enlargement of omnidirectional photonic bandgap in porous silicon dielectric mirrors with a Gaussian profile refractive index. In: Applied physics letters, 2009, vol. 94, no 6, p. 061914. [ Links ]
10. GARTNER, Leslie P.; HIATT, James L. Atlas color de histología. En: Médica Panamericana, 2003. [ Links ]
11. GRANT, Ian S.; PHILLIPS, William Robert. In: Electromagnetism. John Wiley & Sons, 2013. [ Links ]
12. GREINER, Walter. In: Classical electrodynamics. Springer Science & Business Media, 2012. [ Links ]
13. GRUSHINA, N. V., et al. Broad omnidirectional band of reflection from Fibonacci one-dimensional photonic crystals. In: PIERS, 2009, vol. 5, no 6, p. 511-515. [ Links ]
14. GUEVARA FONSECA, J.; MATUZ MARES, D.; VÁZQUEZ MEZA, H. La mitocondria en el centro del universo celular. En: Mensaje bioquímico, 2012, vol. 36. [ Links ]
15. HECHT, Eugene. Optics 4th edition. In: Optics, 4th Edition, Addison Wesley Longman Inc, 1998, 1998. [ Links ]
16. JIANG, Wen, et al. Nanoparticle-mediated cellular response is size-dependent. In: Nature nanotechnology, 2008, vol. 3, no 3, p. 145-150. [ Links ]
17. JOANNOPOULOS, John D., et al. In: Photonic crystals: molding the flow of light. Princeton university press, 2011. [ Links ]
18. JOHNSON, B. L.; WEILER, Jerome T.; CAMLEY, R. E. Bulk and surface plasmons and localization effects in finite superlattices. In: Physical Review B, 1985, vol. 32, no 10, p. 6544. [ Links ]
19. KAVOKIN, A., et al. In: Microcavities Oxford University Press. New York, 2007. [ Links ]
20. KIERSZENBAUM, Abraham L.; TRES, Laura. En: Histología e biología celular. Elsevier Brasil, 2012. [ Links ]
21. LIPSON, Ariel; LIPSON, Stephen G.; LIPSON, Henry. In: Optical physics. Cambridge University Press, 2010. [ Links ]
22. MCCALL, M. W. Axial electromagnetic wave propagation in inhomogeneous dielectrics In: Mathematical and computer modelling, 2001, vol. 34, no 12, p. 1483-1497. [ Links ]
23. MARTORELL, Alejandro. Indagando el origen de las mitocondrias. En: Revista de divulgación de la Facultad de Biología, 2014, vol. 1, no 1. [ Links ]
24. MARTORELL RIERA, Alejandro. Regulación de la dinámica mitocondrial en neuronas sometidas a excitotoxicidad. Tesis Doctoral. Barcelona. Universidad de Barcelona. Departamento de Biología, 2014. 48 p. [ Links ]
25. RAYLEIGH, Lord. LVI. On the influence of obstacles arranged in rectangular order upon the properties of a medium. In: The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1892, vol. 34, no 211, p. 481-502. [ Links ]
26. REITZ, John R. Christy, et al. En: Fundamentos de la teoría electromagnética. 1986. [ Links ]
27. JOHN, Sajeev. Localization of light. In: Phys. Today, 1991, vol. 44, no 5, p. 32-40. [ Links ]
28. SOTO, Alonso Sepulveda. En: Electromagnetismo. Universidad de Antioquia, 2009. [ Links ]
29. SOUKOULIS, C. M. The history and a review of the modelling and fabrication of photonic crystals. En: Nanotechnology, 2002, vol. 13, no 3, p. 420. [ Links ]
30. SPENCER, Michael. En: Fundamentals of light microscopy. Cambridge University Press. 1982. [ Links ]
31. SUKHOIVANOV, Igor A.; GURYEV, Igor V. In: Photonic crystals: physics and practical modeling. Springer, 2009. [ Links ]
32. THAR, Roland; KÜHL, Michael. Propagation of electromagnetic radiation in mitochondria? In: Journal of theoretical biology, 2004, vol. 230, no 2, p. 261-270. [ Links ]
33. WOLFRAM, Stephen, et al. Mathematica. In: Wolfram Research, Champaign, 2009. [ Links ]
34. YABLONOVITCH, Eli. Inhibited spontaneous emission in solid-state physics and electronics. In: Physical review letters, 1987, vol. 58, no 20, p. 2059. [ Links ]
35. ZHAN, Tianrong, et al.Transfer matrix method for optics in graphene layers. In: Journal of Physics: Condensed Matter, 2013, vol. 25, no 21, p. 215-301. [ Links ]