1. Introduction
The study of the satellite galaxies of the Milky Way has been of great interest because they may help answer two fundamental questions about the evolution of galaxies [1]: the actual content of dark matter inside these dwarf galaxies and their implications in the hierarchical formation of the galactic halo.
One of the most interesting members of the Local Group is the Sagittarius dwarf galaxy, discovered in 1995 when R. Ibata et al. [2] did a study on the spheroid of the Milky Way. It is the closest known satellite galaxy to the Milky Way, subtends an angle of ~10° In the celestial vault and is at a galacto-centric distance of 24 ± 2 kpc [2] [3] [4].
Because of this closeness, the Sagittarius progenitor has been exposed to enormous tidal forces. Consequently, Sagittarius has been and continues to be dismembered, leaving as evidence of this interaction a trail of great tidal tails. The study of these tidal tails can reveal the shape of the gravitational potential of the Milky Way and the orbit of Sagittarius. In general, it can be stated that the study of these tidal tails of the satellite galaxies in the Local Group can give important clues about the formation scenarios of galaxies such as the Milky Way [5].
Traditionally it is assumed that the Sagittarius progenitor belongs to the spheroidal type (dSph) [6] [7] [8] [9] [10][11] [12] [13], that is, there are research works trying to reproduce the characteristics observed in the tidal currents of Sagittarius (e.g. [14] [15] [16] [17] [18]), where the progenitor of the dwarf galaxy is a spheroidal galaxy (a distribution of stars and a halo of dark matter), without a subjacent theoretical model that fully explains the data provided by the 2MASS [16] and the SDSS [19] galaxy surveys. These two catalogs have allowed studying in great detail the tidal tails of Sagittarius, showing that these tails have bifurcations, besides constituting a percentage of the galactic halo of the Milky Way. Evidence of a bifurcation in the northern tidal stream of Sagittarius consisting of two branches observed from data from the SDSS DR5 [19].
Here they clearly show how the bifurcation begins around the Galactic North Pole with RA≈180°. The tidal tails are located in (l, b, R) = (350°, 50°, 46 kpc) to the north and (157°, -58°, 33 kpc) to the south [19] [20] [21], where (l, b, R) correspond to the galactic coordinates: galactic longitude, galactic latitude and distance to the Sun, respectively. Branch A is in the lowest declination while branch B is in the highest declination (See Figure 1 in [19]). In [9] it is shown that the trace of the north current of Sagittarius is between RA = 270° and RA = 190°, where the separation distance of branches A and B is ≈ 15 kpc and that there is no evidence that any part of this tidal tail passes through the solar neighborhood. A prominent Sagittarius debris arm extends from the center of this galaxy to the north galactic plane at a distance of ~45 kpc from the Sun and turns toward the top of the galactic north (NGC), from there descends back to the galactic plane.
The distribution of the debris of the Sagittarius tidal tails traces their orbit [9]. The stellar tidal tails present in the halo of the Milky Way produced by accretion of smaller galaxies are a prediction of the hierarchical model of structure formation in the Universe. It has been mentioned that branches A and B were probably formed in different stages according to [18] [19] [22] [23]. In 2006 Fellhauer et al. [23] performed several numerical N-Body simulations of the evolution of a disc-like progenitor of Sagittarius orbiting the Milky Way, which was modeled with a rigid potential.
In their simulations the progenitor of Sagittarius was a Plummer sphere. They were able to reproduce the bifurcations in the tidal streams of Sagittarius only if the potential of the Milky Way is near to spherical. It has been found that these branches have similar distances, velocity distributions and metallicities [24] [25], which would refute the hypothesis that the bifurcations are of different ages or that they are tidal streams of different progenitors [26]. There is no definitive evidence yet about that.
In 2010 Peñarubia et al. [18] considered the possibility that the progenitor of Sagittarius had not been a dSph but a rotating disk galaxy. They sought to examine how tidal currents are affected by rotation without trying to reproduce the observed characteristics of neither the tidal stream nor the current state of the galaxy. For that they used N-body simulations with a rigid potential to model the Milky Way, and found bifurcations in the simulated tidal stream similar to those observed. Table 1 shows the observed physical properties for this satellite galaxy, in addition, it is estimated that the current mass of Sagittarius is Msgr =2-5x108 M⊙ [3].
Based on the work done by [18] and [23], in this paper, we study the possibility that the progenitor of Sagittarius was a rotating disk galaxy and try to reproduce the bifurcations in its tidal tails and the observed physical properties (present) of Sagittarius modeling the Milky Way as a live potential rather than with a rigid potential, as done by [18] and [23]. Some preliminary parts of the research work presented in this paper have been published in proceedings [27]. An extended and detailed documentation about this research can be found in the master's thesis (in Spanish) [28].
This work is organized as follows: in Section 2 we show the structural parameters for each galaxy and the initial orbital conditions in the simulations. In Section 3 we present the results from the simulations, comparing the observed values of position, bifurcations and physical properties found in the cases of interest.
2. Structures and initial conditions
In this work, the Milky Way is modeled as a disk-type galaxy with three components: dark matter halo, stellar disc and stellar spheroid. Sagittarius is considered a disk-type galaxy with two components: a halo of dark matter and a stellar disk. The initial conditions of the possible orbits of Sagittarius are determined by simulating the orbit of a test particle in a rigid potential representing the Milky Way.
2.1 Initial Structures
To generate the initial galactic structures for the Milky Way and Sagittarius, the GALIC software [32] has been used.
GALIC is an open source code for the construction of N-body galaxy models using an iterative method, starting with some initial particle's velocities from an initial mass density distribution. The difference of the time-averaged density response produced by the particle orbits with respect to the initial density configuration is characterized through a merit function, and a stationary solution of the collision-less Boltzmann equation is found by minimizing this merit function directly by iteratively adjusting the initial velocities. The velocity adjustment is done with a stochastic process from an approximate solution of the distribution function, seeking for an improvement of the fit.
The GALIC program requires an input file with the values of the parameters of the galaxy to be created. The values used to create the Milky Way and Sagittarius with GALIC are listed in Tables 2 and 3 respectively.
2.1.1 The Milky Way
For the modeling of the Milky Way galaxy, the parameters are shown Table. Here a h is the radial scale length of the dark matter halo, C is the concentration parameter, ad is the radial scale length of the disk, z d is the vertical scale length of the disk, N h is the number of particles in the dark matter halo, N d is the number of particles in the disc and N b is the number of particles in the bulge. In Figure 1 the initial structure of the Milky Way, projected on the planes xy, yz, xz respectively, is shown.
2.1.2 Progenitor of Sagittarius
For the model of the progenitor of the Sagittarius dwarf galaxy the parameters are shown in Table 3. Figure 2 shows the initial structure of the progenitor of Sagittarius, projected on the planes xy, yz, xz.
The numerical structures obtained with GALIC [32] were simulated under their own gravity with GADGET-2 [33] over a period of time of 2.0 Gyr to ensure virial balance, where the values for the softening length (ε) are shown in Table 4, where εh, εd, εb, are the softening lengths for the particles in the halo, disc and bulge, respectively.
GADGET-2 is an open source code to perform N-body simulations including gas dynamics on massively parallel computers with distributed memory. The gravitational forces are computed with a hierarchical tree algorithm in combination with a particle-mesh scheme for long-range gravitational forces (optional), while the gas dynamics are simulated using smoothed particle hydrodynamics (SPH). GADGET-2 can be used to perform either Newtonian or cosmological simulations over a wide range of scales.
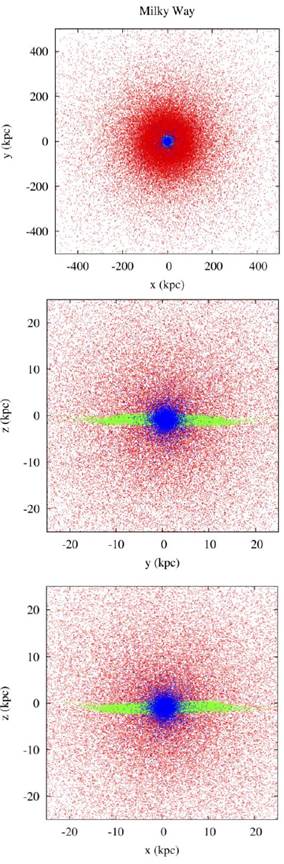
Figure 1 Initial structure of the Milky Way. Projections on the planes xy, yz and xz, respectively, are shown. The colors correspond to the different components of the Galaxy: blue for the bulge, green for the disk and red for the dark matter halo.
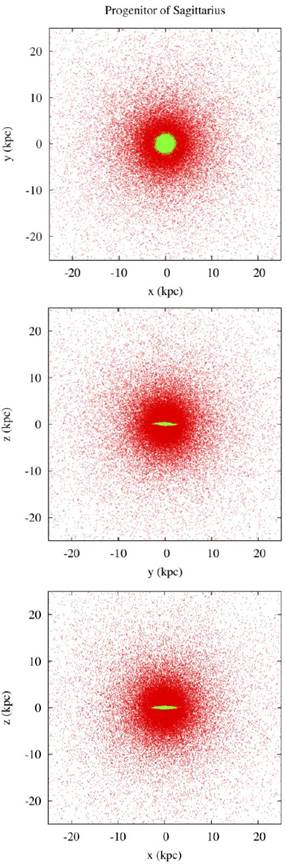
Figure 2 Initial structure of the Sagittarius dwarf. Projections on the planes xy, yz and xz, respectively, are shown. The colors correspond to the different components of the simulated galaxy: green for the disk and red for the dark matter halo.
2.2 Initial Conditions: Orbit
The orbit of a test particle in the rigid potential of the Milky Way was simulated back in time, with an initial radial velocity of 171 km/s and a tangential velocity varying between -325 km/s and 325 km/s, at intervals of 5.0 km/s. For each simulated orbit the pericentric and apocentric distance are calculated taking into account that the observational values for the apocenter are between 50 and 70 kpc and for the pericenter are between 10 and 15 kpc. Initial conditions for the orbit are shown in the table 5.
2.3 Numerical Simulations
For the set of initial conditions in the Table 5 the evolution of the Sagittarius progenitor is simulated using GADGET-2 during 7 Gyr with several angles of inclination θ between the angular momentum of the disc and the angular momentum of the orbit in the range 0° ≤ θ ≤ 180° (see Figure 3). For the simulations the softening lengths shown in Table 4 were used. We constructed a program to set the initial conditions of the orbit of the progenitor and the inclination of the disk respect to the plane of the orbit (angle θ) in the format required by GADGET-2.
The simulations are performed in Cartesian coordinates with the center of the Milky Way at the origin. The positions and velocities of all particles in the simulation are stored in a snapshot file each 0.1 Gyr.
The physical properties of the remnant of Sagittarius to be determined are the central surface brightness, the mass-to-light ratio, the line-of-sight central velocity dispersion and the half-light radius.
To carry out the theoretical calculation of these quantities we perform the following sequence: first we tag the most bound particles of the progenitor at the initial time of the simulation and use them iteratively to compute the position of the center of mass of the object at the following snapshot times, taking care of those particles that are not inside the core anymore.
After this we projected the stars (disc) particles on the sky, as observed from the position of the Sun, that lie inside a circle of a given radius around the center of mass of the remnant; and computed the corresponding quantities following the method described in [34] [35] [36] [37].
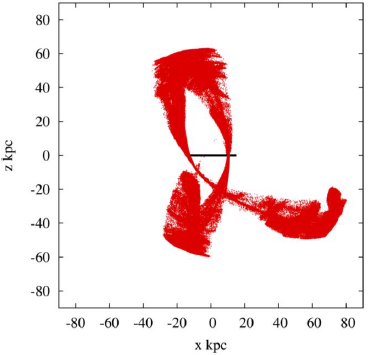
Figure 4 Tidal tails of the dwarf galaxy, projected on the xy plane, as it orbits the Milky Way. The horizontal line shows the position of the disk of the Milky Way. The red dots correspond to the disk particles of the progenitor of Sagittarius.
In order to search for the bifurcations in the tidal tails of Sagittarius we projected the positions of the stars particles (disc) of the dwarf galaxy on the sky using equatorial coordinates in declination-right ascension maps. This was done for each snapshot in each of the simulations we have performed.
3. Results
Figure 5 shows the tidal tails obtained for different angles between the angular momentum of the disc of the dwarf galaxy and the angular momentum of the orbit. It can be observed that the bifurcations are more evident when θ = 130° and θ = 160°.
In addition, since for θ= 130° the bifurcation is more similar to the features observed by the SDSS DR5, we compute the physical properties of the remnant of Sagittarius in this simulation. When θ= 0° and θ= 90° no bifurcation is generated. Our results about the bifurcation for θ= 160° are similar with those obtained by [18] (θ = -20° in their paper).
Along with the loss of particles of the dwarf galaxy due to the tidal forces produced during its interaction with the Milky Way and the deformation of the initial stellar disk, the dwarf suffers a succession of quenching and stretching events.
All these processes combined produce a change in the properties an observer would measure as the remnant of the disk changes its shape and stellar content. Moreover, the observed properties could change with the relative orientation of the remnant respect to the position of the Sun.
Figure 6 shows the time evolution during t = 7.0 Gyr of the central surface brightness, the half-light radius, the central velocity dispersion along the line of sight and the mass-to-light ratio for the progenitor of Sagittarius with an angle θ = 130°. These quantities were computed as described in [36].
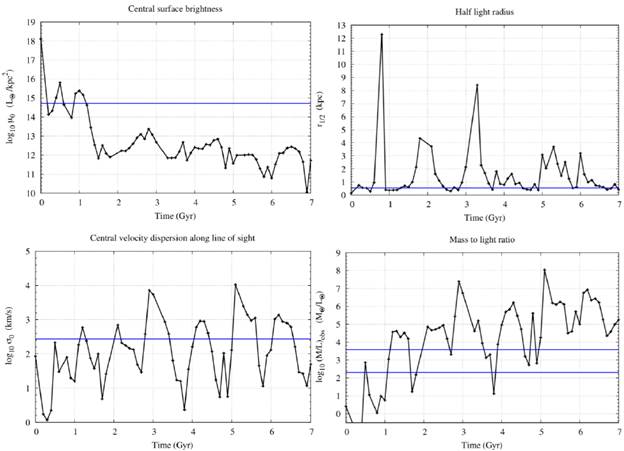
Figure 6 Time evolution of the physical properties of Sagittarius for θ = 130°. The horizontal lines show the corresponding value(s) reported in the literature for each of the properties of Sagittarius (see Table 3). Error bars are of the size of the symbols in the plots.
As we already mentioned, the simulation of interest will be θ = 130° due to the great similarity between the bifurcations found in our simulations and the observational data. For this case, the bifurcation arises in t = 5.0 Gyr and it starts in RA ~170°, the separation between branches is ≈ 15 kpc.
Table 6 shows the results obtained for the physical properties of the remnant of Sagittarius. Recall that the current position of Sagittarius is (RA, dec, R) = (238.7°, -30.5°, 24 kpc). For this simulation although the bifurcation is found it is not possible to locate the remnant in a position close to the present one.
Some physical properties like the mass-to-light ratio and the of central velocity dispersion have a value close to the observed one, while quantities such as the half-light radius and the central surface brightness have values significantly different from those observed. The remnant is closer to the current position when t = 6.6 Gyr.
However, that position is significantly away from the current position and the physical properties of the remnant at that position are quite far from the observational ones.
On the other hand, in the simulation with θ = 160° it is found that the bifurcation appears in t = 5.0 Gyr and it starts at RA 160° and the separation between branches is ≈ 15kpc. Table 7, shows the results obtained for the physical properties of the remnant of Sagittarius when the bifurcation appears and when the remnant is at the position that is closer to the current one, which is t = 6.2 Gyr.
Table 7 shows that, as in the previous case, when the bifurcation appears (t = 5.0 Gyr) the remnant is not close to the actual position and the physical properties are not similar to those observed for this galaxy. Nevertheless, at t = 6.2 Gyr the position of this remnant is close to the observed position and quantities such as the half-light radius and the central velocity dispersion have values close to the current ones.
4. Conclusions
In this study we find the bifurcations in the tidal streams of Sagittarius similar to those observed by SDSS DR5 when θ = 130° and θ = 160° at t = 5.0 Gyr, However, when they appear, the main body of this galaxy is not located at the actual position of Sagittarius; for θ = 130°, close values are found in the mass-to-light ratio and the central velocity dispersion of the main body when the bifurcation becomes evident.
The position of the remnant closest to the observed one occurs when θ = 160° and t = 6.2 Gyr and values close to those observed for the half-light radius and the central velocity dispersion are found, i.e., although the bifurcations and the position of the remnant close to the present one exist, in no case they reproduce simultaneously the position of the remnant and the bifurcations nor is there a set of initial conditions that reproduce all the observational physical properties of this galaxy.
Our results regarding the reproduction of the bifurcation in the tidal streams of Sagittarius are similar to those obtained by [18 and [23], but modeling the Milky Way as a live potential. Thus, confirming their findings. It appears that under the right parameters it is possible to reproduce the bifurcation in the tidal streams of Sagittarius both with a spherical and with a rotating disc galaxy. The problem is still open and further theoretical and observational studies are required. A possible extension of this work would be to perform numerical simulations with other stellar to dark matter ratios in the progenitor and changing the orbital parameters.






















