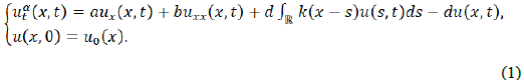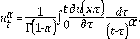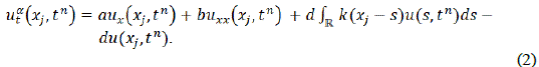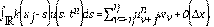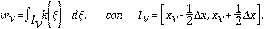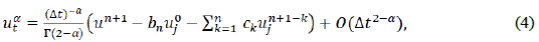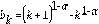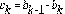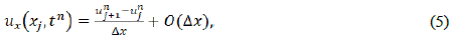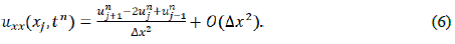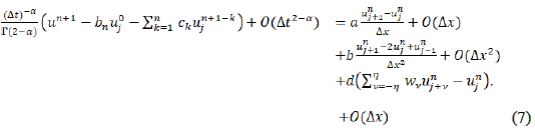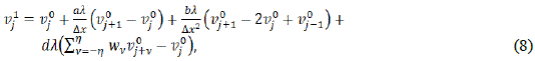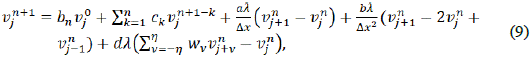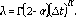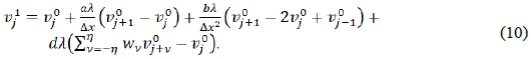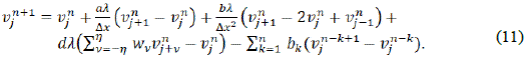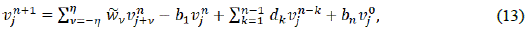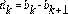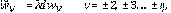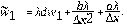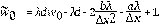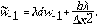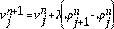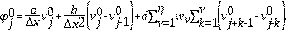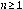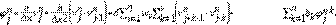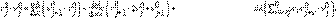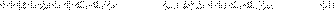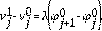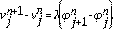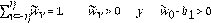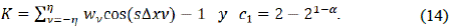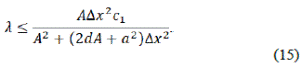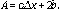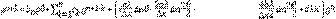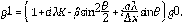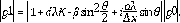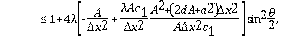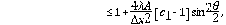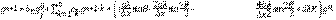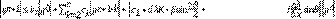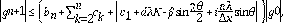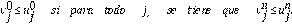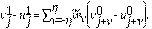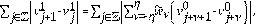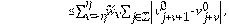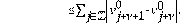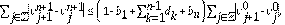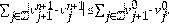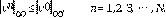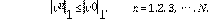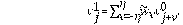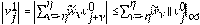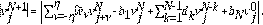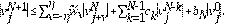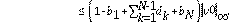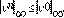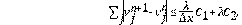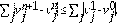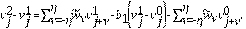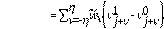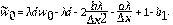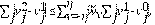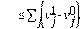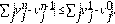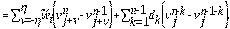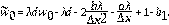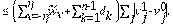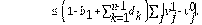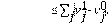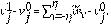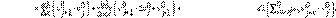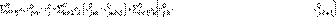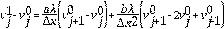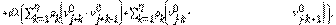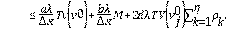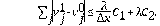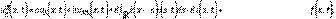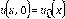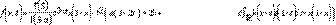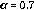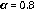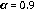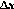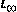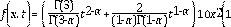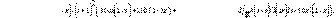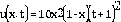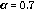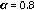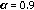I. Introducción
EL desarrollo de la teoría sobre ecuaciones diferenciales fraccionarias se convirtió en un tema de gran importancia, por sus numerosas aplicaciones en las ciencias y las ingenierías [1]-[5]. De esta forma, el objetivo de este artículo es desarrollar un método numérico para hallar oluciones aproximadas de la ecuación de Black-Scholes no local con derivada fraccional en el tiempo, basado en un esquema de diferencias finitas tanto para la derivada fraccional en el sentido de Caputo como para las derivadas espaciales. Además, en la discretización del término no local de la Ec. (1), se usará un kernel con las características de la molificación discreta de [6]. Esto permitirá aplicar las técnicas propuestas para las condiciones de borde de los datos faltantes en los extremos del intervalo de la aproximación.
En los recientes años, muchos autores se han dedicado a estudiar métodos de solución para este tipo de ecuaciones desde un enfoque analítico o numérico. Por ejemplo, en [7]-[12] se construyen soluciones analíticas para modelos no lineales de reacción-difusión o ecuaciones Fokker-Planck las cuales son usadas en la mecánica estadística esencialmente en el análisis del movimiento browniano. Otros trabajos desarrollan aproximaciones numéricas de las ecuaciones diferenciales fraccionarias. Por ejemplo, en [13] y [14] se construyen esquemas numéricos empleando el método de diferencias finitas para el término de difusión fraccional, donde la derivada se define en el sentido de Caputo. De manera similar, en [15] y [16] se considera la derivada de Caputo en ecuaciones no lineales, definiendo esquemas numéricos basados en el método de diferencias finitas. Otros estudios, como en [17]-[19], se aplican las derivadas fraccionarias para valores entre 1 y 2, utilizando discretizaciones de diferencias finitas para sus respectivas soluciones numéricas. Además, en [20], se desarrollan otros métodos mediante OHAM (Optimal Homotopy Asymptotic Method) para obtener un esquema numérico de una ecuación de reacción difusión fraccionaria, y en [21] se desarrollan soluciones de la ecuación de difusión fraccional en el espacio mediante el método de lines y splines.
Consideramos el siguiente problema de valor inicial,
De la misma manera que en [22] y [23], las constantes
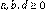 , y el kernel
, y el kernel
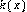 es una función simétrica que decae suavemente de
es una función simétrica que decae suavemente de
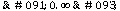 y
y
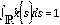 . Además, se exige que la condición inicial sea Lipschitziana y
. Además, se exige que la condición inicial sea Lipschitziana y
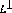 . Para la derivada fraccional en el tiempo se limita el valor
. Para la derivada fraccional en el tiempo se limita el valor
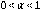 con la definición en el sentido de Caputo, es decir:
con la definición en el sentido de Caputo, es decir:
El desarrollo del artículo se estructura de la siguiente forma: En la Sección II se construye el modelo numérico de la Ec. (1) usando diferencias finitas y la técnica de molificación discreta. Luego, en las Secciones III y IV se incluye las pruebas de estabilidad, regularidad, monotonía, propiedad TVD y las desigualdades relacionadas con la norma 1 y la norma
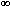 . En la Sección V, se desarrollan los experimentos numéricos para determinar los errores de la aproximación y ordenes de convergencia con diferentes
. En la Sección V, se desarrollan los experimentos numéricos para determinar los errores de la aproximación y ordenes de convergencia con diferentes
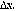 , y se finaliza con las conclusiones del trabajo.
, y se finaliza con las conclusiones del trabajo.
II. Aproximación numérica
Para la discretización de la ecuación (1) se define una malla en los puntos
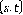 . Tomando
. Tomando
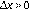 y
y
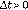 , donde
, donde
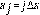 y
y
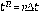 para
para
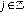 y
y
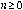 . Sustituyendo los anteriores valores en la Ec. (1), se obtiene que:
. Sustituyendo los anteriores valores en la Ec. (1), se obtiene que:
Para construir el esquema numérico de la Ec. (2) se plantea las siguientes discretizaciones: el término no local se apróxima por el método utilizado en [24]. De tal forma, se tiene:
donde,
La derivada fraccional en el tiempo se discretiza usando el método de diferencias finitas como en [24] y [25],
Las aproximaciones para los términos de la convección y la difusión de la Ec. (2), se expresan de la siguiente forma:
Reemplazando las ecuaciones (3), (4), (5) y (6) en la Ec. (2), obtenemos que:
De la ecuación (7) tenemos la siguiente discretización:
Es necesario reorganizar los esquemas numéricos de las Ec. (8) y Ec. (9), para facilitar las demostraciones de los lemas y la implementación de los experiementos numéricos. De tal forma que se obtengan las siguientes ecuaciones equivalentes:
En los experimentos numéricos se empleará la siguiente discretización. Esto permitirá construir la matriz de condición de borde para los datos faltantes en los extremos de los intervalos donde se aproxima la solución.
A continuación, se probará el lema 2.1 para la aproximación numérica en las Ec. (10) y Ec. (11). Este lema garantiza que el esquema propuesto tiene la propiedad de conservación, característica importante en las soluciones de los problemas de aplicación, condición que se debe mantener en las aproximaciones numéricas.
Lema 2.1 (Ley de conservación) El esquema numérico de la Ec. (10) y Ec. (11) tiene la forma conservativa:
Demostración. Probaremos primero el caso para
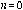 , sea
, sea
Suponemos que para los
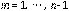 la igualdad se cumple. Ahora los probaremos para
la igualdad se cumple. Ahora los probaremos para
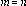 .
.
III. Estabilidad
En esta sección analizaremos la estabilidad del esquema en la Ec. (9), mediante el método de Von Neumann para diferencias finitas bajo las siguientes condiciones:
Lema 2.2 El esquema en la ecuación (9) es estable bajo las condiciones Ec. (14) y
Demostración. Sea
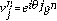 , reemplazando en el esquema numérico Ec. (9) se obtiene:
, reemplazando en el esquema numérico Ec. (9) se obtiene:
Debemos probar que
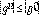 , primero se mostrara el caso
, primero se mostrara el caso
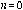
donde
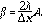 . Aplicando el modulo a ambos lados de la ecuación anterior, se tiene que:
. Aplicando el modulo a ambos lados de la ecuación anterior, se tiene que:
Por lo tanto, tenemos la siguiente igualdad:
Como
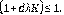 ,
,
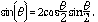 ,
,
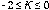 y dada la condición Ec. (14),
y dada la condición Ec. (14),
Asumimos que la desigualdad
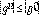 se cumple hasta
se cumple hasta
 . Probaremos para el caso
. Probaremos para el caso
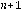 .
.
Sea,
Aplicando el modulo en la ecuación anterior, obtenemos la desigualdad
Por inducción,
Tenemos que,
De la siguientes condiciones
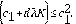 ,
,
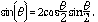 ,
,
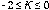 y de Ec. (14), obtenemos la siguiente desigualdad:
y de Ec. (14), obtenemos la siguiente desigualdad:
Por lo tanto,
IV. Monotonía
A continuación, se probará la monotonía del esquema numérico, así como las condiciones de regularidad y TVD. Definimos la monotonía del esquema de aproximación de la siguiente forma: Sean dos discretizaciones de Ec. (13)
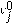 y
y
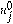 , se dice que el método es monótono si satisface
, se dice que el método es monótono si satisface
Lema 4.1 El esquema numérico en la Ec. (13), es monótono bajo la condición CFL.
Demostración. Suponemos que
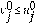 , probemos el sistema para
, probemos el sistema para
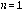 , tenemos que:
, tenemos que:
Vamos a suponer que para
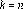 se cumple la monotonía del sistema. Probaremos el caso
se cumple la monotonía del sistema. Probaremos el caso
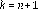 .
.
bajo las condiciones CFL tenemos que,
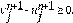 .
.
Ahora demostraremos algunas propiedades de regularidad de del esquema numérico.
Lema 4.2 Bajo la condición de estabilidad se cumple la propiedad TVD.
Demostración. Probemos el caso
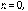 , tenemos que,
, tenemos que,
entonces:
Suponemos que se cumple la propiedad TVD para los valores
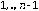 . Ahora en el caso
. Ahora en el caso
 , tenemos que:
, tenemos que:
El término
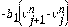 se puede agrupar con
se puede agrupar con
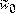 , de tal forma que
, de tal forma que
Por inducción,
Por lo tanto,
Lema 4.3 Bajo la condición de estabilidad se cumplen las siguientes desigualdades.
Demostración. Para
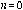 el esquema en la Ec. (13) toma la siguiente forma
el esquema en la Ec. (13) toma la siguiente forma
tenemos que,
Por inducción suponemos que se cumple para
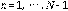 , ahora lo probaremos para
, ahora lo probaremos para
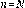
De la misma forma que el Lema 4.2 se tiene que:
La demostración para la desigualdad
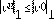 es similar a la prueba de la propiedad TVD.
es similar a la prueba de la propiedad TVD.
Lema 4.4 Bajo la condición CFL, se cumple que
donde
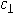 y
y
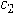 son constantes que no dependen de
son constantes que no dependen de
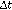 y
y
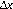 .
.
Demostración. Se demostrara primero la desigualdad
Entonces,
Suponemos que para valores hasta
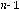 , se cumple que
, se cumple que
De igual forma que en el caso
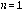 , se tiene que
, se tiene que
Obtenemos la siguiente desigualdad
Finalmente, de la Ec. (12) implica que
Como en [9], tenemos que
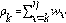 , donde
, donde
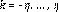 , de tal forma podemos escribir como:
, de tal forma podemos escribir como:
de modo que,
Entonces,
Tenemos que,
donde
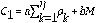 y
y
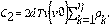 . De esta forma reemplazando en la Ec. (16) completamos la prueba.
. De esta forma reemplazando en la Ec. (16) completamos la prueba.
V. Experimentos numéricos
En los experimentos numéricos se adiciona un término fuente en la Ec. (1). Usando esta nueva expresión podemos obtener una solución exacta del problema, y asi realizar el respectivo análisis de error y de orden de convergencia mediante el esquema en la Ec. (13). Este análisis se realizó para valores de
 iguales a 0.7, 0.8 y 0.9 en la derivada de Caputo. Las condiciones iniciales se aproximan a cero en los extremos del intervalo de la variable espacial, donde se pretende encontrar la solución numérica. La condición anterior se debe implementar con el fin se usar la matriz de condición de borde de cero propuestas en [6] y [22], para compensar los datos faltantes en los límites del intervalo.
iguales a 0.7, 0.8 y 0.9 en la derivada de Caputo. Las condiciones iniciales se aproximan a cero en los extremos del intervalo de la variable espacial, donde se pretende encontrar la solución numérica. La condición anterior se debe implementar con el fin se usar la matriz de condición de borde de cero propuestas en [6] y [22], para compensar los datos faltantes en los límites del intervalo.
Vamos a considerar la siguiente ecuación de Convección-Difusión no local con derivada fraccional en el tiempo para los experimentos numéricos:
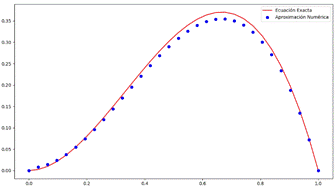
A continuación encontramos los ejemplos con las tablas y gráficas respectivas, que verifica el comportamiento de la aproximación numérica y el orden de convergencia 1 del esquema en la Ec. (7).
Ejemplo 5.1 Sean
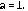 ,
,
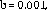 ,
,
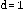 y el tiempo
y el tiempo
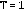 . Consideramos un intervalo en
. Consideramos un intervalo en
 de
de
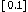 , el kernel
, el kernel
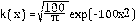 y el término fuente
y el término fuente
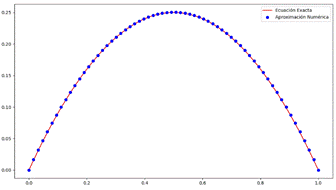
El problema anterior tiena la solución exacta:
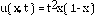
A continuación se muestra la Tabla I de errores para diferentes valores de
 , y la Fig. 1 con la comparación de la solución exacta y la aproximación numérica para
, y la Fig. 1 con la comparación de la solución exacta y la aproximación numérica para
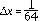 .
.
Ejemplo 5.2 Sean
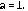 ,
,
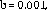 ,
,
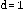 y el tiempo
y el tiempo
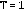 . Consideramos un intervalo en
. Consideramos un intervalo en
 de
de
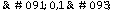 , el kernel
, el kernel
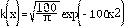 y el término fuente,
y el término fuente,
El problema anterior tiene la solución exacta:
A continuación se muestra la Tabla II de errores para diferentes
 , y la Fig. 2 con la comparación de la solución exacta y la aproximación numérica para
, y la Fig. 2 con la comparación de la solución exacta y la aproximación numérica para
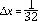 .
.
VI. Conclusiones
A partir del estudio realizado, se obtuvo un esquema numérico explícito con orden de convergencia 1. En el desarrollo del método numérico se probaron la ley de conservación, la monotonía y la propiedad TVD, además de otras propiedades que son necesarias, pero no suficientes en la convergencia del esquema. Los experimentos numéricos coinciden con el desarrollo teórico del método. Sin embargo, se observó que el algoritmo de aproximación tiene un costo computacional alto debido a la condición CFL. Por esta razón, se optó por utilizar valores pequeños del parámetro
 , lo que permitió reducir los tiempos de ejecución y los requerimientos computacionales.
, lo que permitió reducir los tiempos de ejecución y los requerimientos computacionales.
La derivada fraccional temporal en el sentido de Caputo requiere que se almacenen todos los valores
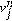 para el cálculo del siguiente término
para el cálculo del siguiente término
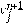 , esto genera una carga significativa en la memoria de la computadora durante la ejecución de la rutina.
, esto genera una carga significativa en la memoria de la computadora durante la ejecución de la rutina.