INTRODUCTION
The Department of Boyaca has been characterized by the production of deciduous fruit trees thanks to edaphoclimatic conditions that are conducive to their establishment. In addition, farmers here are experienced and have a long tradition of producing deciduous species. This department has achieved one of the higher yields in the country for fruit species, such as plums, pears, apples and peaches (Ducuara-Cabrera, 2017), where the peach tree is one of the better adapted to tropical conditions (Pinzón et al., 2014; Quevedo-García et al., 2017). However, peach trees from temperate zones present a different phenological cycle than tropical crops because the flowering-harvest phenological stages are largely determined by the average post-flowering temperature (Pola et al., 2016). For this reason, the dynamics of fruit growth and development must be understood for the different peach varieties to plan cultivation tasks.
The growth of the so-called stone fruit trees, including the peach tree, has been generally described as double sigmoid (Silva et al., 2019). However, this statement is not entirely consistent because there are many peach cultivars that differ in terms of their phenological cycle, highlighting the presence of short-cycle materials that follow a sigmoid behavior, while intermediate and long-cycle cultivars follow a double sigmoid behavior (dela Bruna, 2007; Della Bruna and Moreto, 2011). To characterize the growth behavior of peach fruits and other organs, variables such as height, weight, and diameter, among others, have been used, most commonly with regression models (Casierra-Posada et al., 2004; Quevedo et al., 2017). However, non-linear regression models have strong advantages over linear regression models, such as conservation of resources, in the cases of simple non-linear models, and biological interpretation of estimated parameters (Fernandes et al., 2014; Muianga et al., 2016).
Nonlinear regression models are commonly selected as an important alternative for the analysis of data from agricultural processes (Archontoulis and Miguez, 2015) because they are simple, have flexibility and are conserve resources. Nonlinear models can often be easier to interpret than alternatives although objectives and applications may vary.
Growth models can be classified into two large groups: those that assume that there is an asymptotic final size, and those that do not. The choice between asymptotic and non-asymptotic functional forms depends in part on the response variable of interest and the time scale of the study. Asymptotic models are also appropriate for analyses that include the entire life cycle, while non-asymptotic models implicitly assume that growth continues indefinitely (Paine et al., 2012).
Growth curves are a useful tool for modeling natural events that involve response changes over time (Szabelska et al., 2010). For a given model, time is a continuous variable instead of a discrete one, where the main condition for generating growth curves is the existence of a functional relationship between the response variable and time (Hanusz et al., 2008). This type of curve generally has a sigmoid appearance (S-shaped) that is adjusted with nonlinear regression models because the parameters have direct practical interpretation, which is why non-linear models are widely used in growth studies for different species (Leal do Prado et al., 2013; Sari et al., 2019; Menezes da Silva et al., 2020).
Sigmoid curves can be generated from mathematical functions from non-linear models and are commonly used to describe variables such as height, weight, leaf area index or seed germination as a function of time (Miguez et al., 2018). In general, the suitability of a sigmoid equation to estimate the maximum rate of increase or the optimal x level to maximize the value of y is important (Yin et al., 2003). There are several models that generate curves with a sigmoid pattern, such as logistic, Gompertz, Richards or Weibull (Miguez et al., 2018). Their equations have an inflection point, where the growth rate increases up to the inflection point and then decreases. For this reason, they can be used to analyze processes with two growth phases (Shabani et al., 2018).
Studies have been carried out on the growth and development of peach fruits; however, most were conducted in temperate zone conditions to elucidate growth dynamics but do not represent the fruit growth conditions in tropical and subtropical zones, where the ecophysiological conditions are different (Fischer et al., 2011). For this reason, this research aimed to understand the dynamics of fruit growth based on the thermal time of the Dorado variety, grown in the Colombian high tropics, using different non-linear mathematical models.
MATERIALS AND METHODS
Data collection
The fruits used for the determination of the mathematical growth models were collected from the La Esperanza farm, located in the Agua Blanca district in the municipality of Tuta-Boyaca (Colombia), with the geographical coordinates: 5°41'24'' N and 73°13'35'' W, located at an altitude of 2,640 m a.s.l., with an average annual rainfall of 1,216 mm, average temperature of 14ºC and relative humidity of 85%, determined with an RHT20 datalogger (Extech™). The Dorado variety was selected because it is one of the more cultivated and accepted varieties in the domestic market. According to Campos (2013), this cultivar is adapted to 2,200 to 2,700 m a.s.l., requires 300 h with temperatures below 7.2°C when dormant, and has good acceptance in the market because of its yellow skin with slight red pigmentation, yellow pulp with reddish coloration around the stone, rounded shape, and average weight of 150 g. It is consumed fresh and used in agribusiness.
To quantify the growth variables, 15 sampling units were taken, each composed of three trees that were randomly selected. The sampling was carried out every 15 d, starting from stage 65 (full flowering) and lasting until the fruits reached full bloom, optimal growth and consumption maturity stage 89 according to the BBCH scale (Meier, 2001), with a total of 9 samplings (135 days after full flowering (daff)).
Methodology
45 trees were randomly selected, three for each estimated sampling point. 100 flowers/plant with mixed branches in year one were marked, guaranteeing 25 fruits/plant in the sampling points. The selected peach trees were 7 years old and planted at a distance of 3 m between plants and 2.5 m between rows. At the start of full flowering (floral opening of 50% of the flowers), corresponding to stage 65 according to the BBCH scale (Meier, 2001), they were marked with silicone rubber. In each sampling, the fruits were manually collected from the trees and packed in paper bags that were placed in a polystyrene thermos. The collection was done in the afternoon so that the analyses could be carried out in the morning hours of the next day. 10 repetitions were carried out for the growth variables (Tab. 1), each composed of a fruit.
Table 1. Equations used to determine AGR and RGR (Hunt, 2017).
| Index | Description | Equation | Units |
|---|---|---|---|
| AGR | Absolute growth rate |
|
g d-1 |
| RGR | Relative growth rate |
|
g g-1 d-1 |
W = total dry mass (g); d W / dt = variation of dry mass as a function of thermal time.
The accumulation of growing degree day (GDD) was determined using the residual method (Torres, 2006), using the following equation (1)
Where, Tm is the mean daily air temperature, calculated from the daily temperature quantified every 30 min using an RHT20 humidity and temperature datalogger (Extech ™); Tbase was defined from the physiological point of view as the value of the temperature under which the development of a crop or a specific organ of a plant stops (Trudgill et al., 2005), which for this study was assumed as 4.5°C according to Chaar and Astorga (2012)
The evaluated growth variables were: fresh weight, which was quantified for the endocarp (seed and shell) and the edible part (pulp (mesocarp) + rind (epicarp)) using a sample of 10 fruits taken at each sampling point and recording the weight individually using an Acculab® VIC 612 precision balance with an approximation of 0.01 g; dry weight for the endocarp (seed-bone) and the edible part (pulp + rind) using a sample of 10 fruits taken at each sampling point and independently placing the fruits in a Memmert® drying oven at a temperature of 75°C until constant weight; polar diameter, which was obtained as the distance between the apical and basal area of the fruits using a Mitutoyo digital caliper with a precision of 0.05 mm; and suture diameter as the distance at the equatorial zone using a Mitutoyo digital caliper with a precision of 0.05 mm.
The parameters were estimated with the total dry weight data to calculate the absolute growth rate (AGR) and relative growth rate (RGR) with the equations in table 2.
Table 2. Definition of models and parameters to evaluate the growth of the P. persica cv. Dorado fruits.
| Model | Equation | Parameter definition |
|---|---|---|
| Logistic model |
|
Where, Y is the response variable (eg, biomass or diameter), t is the explanatory variable (eg Growth Day Degrees (GDD)), Y asym or Y max is the asymptotic or maximum Y value, respectively, t m is the inflection point where the growth rate is maximized, and k refers to the inflection point of the curve |
| Gompertz model |
|
|
| Weibull model |
|
To characterize the fruit growth, the following non-linear regression models were adjusted using the parameterization recommended by Miguez et al., (2018) for the case of the logistic and Gompertz models. In the case of the Weibull model, the parameterization recommended by Ritz and Streibig (2005) (Tab. 2).
A descriptive analysis was carried out, in which the average and standard error were determined for each of the variables evaluated at each of the sampling points. The behavior of each variable with respect to thermal time (GDD) was plotted with the data. The most suitable regression model was determined for each dependent variable. The parameters were estimated using R version 4.0.5 with the 'drc' package, which optimizes the estimation of the parameters using the Gauss-Newton algorithm. The initial assumption of the vector of residuals was verified using the Shapiro-Wilks hypothesis tests for normality, Durbin-Watson, independence and constant variance with the Breusch-Pagan test. The best model was selected with the Residual Standard Error (RSE), Akaike's Information Criterion (AICc) (Hurvich and Tsai, 1993), and Bayesian Information Criterion (BIC) (Raftery, 1986).
RESULTS AND DISCUSSION
The models were adjusted for each of the growth variables. Then, the assumptions of the residual vector were verified, reaching the conclusion that none of these assumptions were violated at the 5% significance level, that is, the vectors had normal values, distribution with zero mean, and independent and constant variance.
Accordingly, each parameter obtained for each model was evaluated (Tab. 2). The three-parameter logistic model was the best model for the fresh and dry weight gain for both the pulp and the endocarp, with parameters significant at 5%. The Gompertz with three parameters was the best model for the polar and suture diameters with parameters significant at 5%. Although the models presented good performance when evaluated using the information criteria, the logistic model presented a lower value for the AICc, BIC and RSE (Tab. 3) in all variables for the fresh and dry weights. The Weibull model presented non-significant parameters for the fresh and dry weights of the pulp, polar diameter and suture diameter and presented the highest values of AICc, BIC and RSE (Tab. 3), making it unreliable for estimating the models for the growth variables in this study.
Table 3. Non-linear models, estimated parameters and information criteria for growth variables of the peach fruit cv. Dorado.
| Model | Variable | Estimated parameters | Data criteria | RSE | |||
|---|---|---|---|---|---|---|---|
| Y asym | k | t m | AICc | BIC | |||
| Logistic | Fresh weight of pulp | 693.57* | -0.00497* | 1,272.47* | 74.15 | 55.93 | 4.06 |
| Fresh weight of endocarp | 12.278* | -0.0072* | 570.79* | 35.75 | 17.54 | 0.48 | |
| Dry weight of pulp | 49.861* | -0.0047* | 1,135.28* | 37.17 | 18.96 | 0.45 | |
| Dry weight of endocarp | 6.112* | -0.0111* | 691.82* | 14.44 | -3.76 | 0.14 | |
| Polar diameter | 7.695* | -0.00284* | 449.38* | 26.65 | 8.44 | 0.29 | |
| Suture diameter | 7.671* | -0.00369* | 462.87* | 29.11 | 10.9 | 0.33 | |
| Gompertz | Fresh weight of pulp | 4518.35NS | -0.00109NS | 2,132.83* | 79.41 | 61.41 | 5.45 |
| Fresh weight of endocarp | 13.274* | -0.0042* | 496.01* | 37.06 | 18.84 | 0.51 | |
| Dry weight of pulp | 252.35NS | -0.0011NS | 1,869.30* | 34.65 | 16.44 | 0.52 | |
| Dry weight of endocarp | 6.401* | -0.0069* | 639.90* | 25.29 | 7.08 | 0.26 | |
| Polar Diameter | 8.721* | -0.0016NS | 321.049* | 23.94 | 5.73 | 0.25 | |
| Suture diameter | 8.687* | -0.00214* | 358.93* | 25.10 | 6.89 | 0.26 | |
| Weibull | Fresh weight of pulp | 24114.0NS | -0.6913* | 10,586.5NS | 85.78 | 67.57 | 7.76 |
| Fresh weight of endocarp | 18.331* | -1.5050* | 583.37* | 40.04 | 21.82 | 0.61 | |
| Dry weight of pulp | 1345.0NS | -0.6324* | 10,238.3NS | 41.73 | 23.52 | 0.67 | |
| Dry weight of endocarp | 6.802* | -4.398* | 646.05* | 27.53 | 9.32 | 0.30 | |
| Polar diameter | 33.188NS | -0.2367* | 9,263.21NS | 38.52 | 20.30 | 0.56 | |
| Suture diameter | 42.117NS | -0.2963* | 7,929.08NS | 33.59 | 15.38 | 0.42 | |
* Parameter significant at 5%; ns: non-significant parameter; Y asym is the asymptotic or maximum Y value, k refers to the inflection point of the curve, and t m is the inflection point where the growth rate is maximized, AICc: Akaike's Information Criterion, corrected; Bayesian Information Criterion (BIC); Residual Standard Error (RSE).
The accumulated growth of the peach fruit cv. Dorado followed a sigmoid behavior, represented by the three-parameter logistic model, which is characteristic of short-cycle peach cultivars (Dela Bruna, 2007), regardless of the model type used to describe. This growth presented three phases. Phase I was characterized by rapid growth as the result of cell division, moving to phase II, in which there were important changes at the physiological and anatomical levels, including a temporary decrease in pulp mass gain, increased endocarp mass, accumulation of substances such as lignin and others involved in endocarp lignification and partial or total seed formation (Cunha et al., 2007; Dela Bruna, 2007). Phase III was characterized by physical and biochemical changes that are typical of the ripening process, such as: increased production of ethylene and other volatiles, color changes, increased respiratory rate, decreased firmness and chemical transformations that affect sugars, organic acids, proteins, phenolic compounds, pigments and pectins (Almanza et al., 2015).
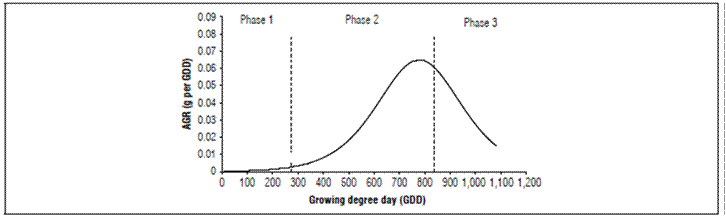
The evaluated material presented fruit set one month after full flowering (stage 65). Afterwards, the fruits began the first growth phase, characterized by active cell division. This phase lasted 30 d and accumulated 273.5 GDD. A second phase of cell expansion and simultaneous lignification of the endocarp lasted for 60 days and accumulated 561.8 GDD. A final phase of fruit maturation lasted 33 d and accumulated 246.5 GDD. This cultivar accumulated a total of 1081.8 GDD in a period of 153 daff (Fig. 1 and 2).
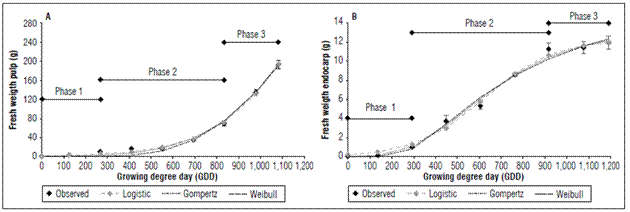
Figure 1. Mathematical modeling of fresh weight in pulp (A) and endocarp (B) of the peach fruit cv. Dorado.
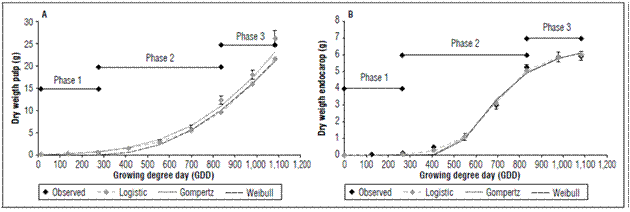
Figure 2. Mathematical modeling of dry weight in pulp (A) and endocarp (B) of the peach fruit cv. Dorado.
The Dorado cultivar presented a fresh endocarp weight (stone and seed) with a final value of 11.95±0.67 g and a dry weight of 5.93±0.26 g (Fig. 1A and 2A). The fresh pulp had a maximum value of 192.63±8.27 g, which corresponded to a pulp dry weight of 22.06±1.50 g. Previous values were 1,081.8 GDD (153 ddpf) (Fig. 1B and 2B).
The polar and suture diameters presented a constant increase that was adjusted to the Gompertz model with three parameters. The polar diameter had a final value of 6.80±0.11 cm, and the suture diameter had a final value of 7.27±0.15 cm (Fig. 3A and B). Increases in diameters and volume in fleshy fruits, including the peach, depend on epidermal extensibility (Thompson, 2001). While epidermal cells divide throughout fruit development, the division in the pericarp is limited to a short period of development and is located in the external tissues around the vascular bundles and in the hypodermis. Once cell division ends, cell expansion begins, increasing fruit size (Bertin, 2005).
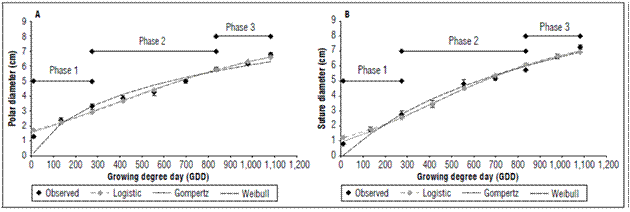
Figure 3. Mathematical modeling of the polar diameter (A) and suture diamter (B) of the peach fruit cv. Dorado.
In addition, the size and final diameter of an organ is related to its dumping power because it is the capacity or potential demand to accumulate assimilates and water (Marcelis and Heuvelink, 2007). As such, fruits are the main sink organs that compete with each other, as do vegetative organs, for the available assimilates (Peil and Galvez, 2005).The logistic, Gompertz, and Weibull models were evaluated to obtain the parameters for the total dry weight for calculating the AGR and RGR. Although the models presented significant parameters, the logistic model was the best model because it presented lower AICc, BIC and RSE values (Tab. 4).
| Variable | Model | Estimated parameter | Data criteria | RSE | |||
|---|---|---|---|---|---|---|---|
| Y asym | k | t m | AICc | BIC | |||
| Total dry weight | Logistic | 29.0515* | -0.00898* | 778.221* | 41.03 | 22.03 | 0.64 |
| Gompertz | 34.330* | -0.00453* | 742.20* | 50.86 | 32.86 | 1.10 | |
| Weibull | 44.053* | -2.6361ns | 805.293ns | 53.27 | 35.06 | 1.27 | |
AICc: Akaike's Information Criterion, corrected; Bayesian Information Criterion (BIC); Residual Standard Error (RSE). Y asym is the asymptotic or maximum Y value, k refers to the inflection point of the curve, and t m is the inflection point where the growth rate is maximized.
The AGR and RGR were evaluated with the three-parameter logistic model. The RGR slowly increased during phase I of growth and increased rapidly until reaching its maximum point at 790.3 GDD (114 daff), with a gain of 0.0650 g GDD-1. It then decreased continuously until harvest (Fig. 4), that is, the maximum growth rate occurred in phase II, as reported for some fleshy fruits.
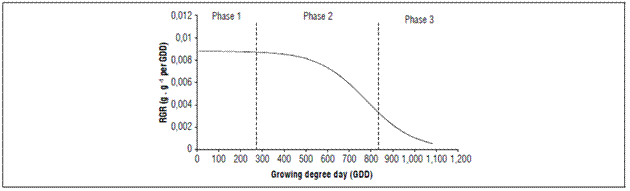
The RGR had a continuous decrease but its decrease was more marked, from 469.4 GDD (80 daff). At the beginning the RGR was 0.01548 g g-1 GDD-1 and, at harvest, it was 0.001501 g g-1 GDD-1 (Fig. 5).
Since the relative growth rate expresses the increase in dry mass of the plant or its organs in time intervals, based on the initial value of the dry mass produced and accumulated, the RGR tended to decrease during the fruit growth and development, as has been reported for this cultivar (Carranza et al., 2009).
CONCLUSIONS
This research corroborated the efficiency of non-linear models for describing the growth of different plant organs or parts. In this case, it was determined that the logistic model with a sigmoid type curve was the most accurate model for the short-cycle peach materials, while the Gompertz model was the most adjusted when the diameter was described. These results agree with those from reports on growth models in different fruit types.
This research evidenced the importance of applying statistical processes, specifically the modeling of growth variables with the Logistic and Gompertz non-linear models, which adequately described the growth curves of the peach cultivar 'Dorado' and generated parameters with practical interpretations that represented the studied biological phenomenon.




![Symptoms and growth components of feijoa (Acca sellowiana [O. Berg] Burret) plants in response to the missing elements N, P, and K](/img/en/prev.gif)