1. Introducción
La valoración de las matemáticas inmersas en prácticas cotidianas, ha sido objeto de estudio en las investigaciones fundamentadas en la Etnomatemática porque permite estudiar los conocimientos matemáticos utilizados y desarrollados por diferentes personas o grupos culturales (Gerdes, 2013). La mayoría de las investigaciones enmarcadas en un programa de investigación (Etnomatemática), inclusivo y preocupado por las prácticas cotidianas, han asumido que la Etnomatemática es: “la matemática practicada por […] comunidades urbanas o rurales, grupos de trabajadores, clases profesionales, niños de cierta edad, sociedades indígenas y otros grupos que se identifican por objetivos y tradiciones comunes a los grupos” (D’Ambrosio, 2001).
D’Ambrosio (2014), caracteriza la Etnomatemática desde su etimología, mencionando que está conformada por tres raíces: las tics o ticas (modos, estilos, artes, y técnicas) de matemá (para explicar, aprender, conocer, lidear en/con) en un determinado etno (ambientes naturales, sociales, culturales); es decir, la Etnomatemática son las ticas de matema en un determinado etno. No obstante, Aroca (2016), manifiesta que la etimología del término Etnomatemática debe ser más abarcadora, por lo que propone la definición siguiente:
(…) No sólo es lo sociocultural, también es lo histórico, lo político, lo ético, su relación con la educación, la formación, la pedagogía, la didáctica, lo religioso, lo económico, lo psicológico, lo lingüístico que median en la enseñanza y aprendizaje de las matemáticas, y no a todas estas dimensiones las podemos interpretar mediante las ticas de mathema en una etno. (Aroca, 2016, p. 192)
En las investigaciones sobre aspectos geométricos, procesos de medición y diseños, se han identificado medidas y patrones de diferentes tipos, que son importantes para la enseñanza y el aprendizaje de las matemáticas (National Council of Teachers of Mathematics, NCTM, 2000). Por ello, a continuación se presenta un estado del arte de investigaciones sobre medidas y patrones desde la Etnomatemática.
Los estudios relacionados con el uso de unidades de medida no convencionales en prácticas cotidianas, como: la carpintería, la pesca y la elaboración de tortillas, han reportado el uso de partes del cuerpo (Chieus, 2009; Castro, Rodríguez-Nieto, Aravena, Loncomilla & Pizarro, 2020; Rodríguez-Nieto, 2020; Rodríguez-Nieto, 2021; Rodríguez-Nieto, Mosquera & Aroca 2019). Asimismo, se ha reportado el uso de artefactos u objetos diseñados por la propia comunidad para realizar mediciones (Blanco-Álvarez, Fernández-Oliveras & Oliveras, 2017; García-García & Bernandino-Silverio, 2019; Paternina-Borja, Muñoz-Granados, Pacheco-Muñoz, & Aroca, 2020; Rodríguez-Nieto et al., 2019; Rodríguez-Nieto, Morales-García, Muñoz & Navarro, 2017; Zambrano, 2012). Particularmente, la actividad de medir juega un papel fundamental en el desarrollo de las ideas matemáticas, y se ocupa de comparar, ordenar y cuantificar cualidades que tienen valor e importancia (Bishop, 1999).
En el sector agrícola, se han reportado unidades de medida no convencionales utilizadas en el proceso de siembra y/o cosecha de algunos productos. En Ávila (2014), se muestran: la tarea o el jornal utilizada para medir superficies agrícolas con base en el tiempo; el zote definida como una capa rectangular conformada por mazorcas colocadas una al costado de otra para calcular la cosecha de maíz, y el paso como unidad de medida en la siembra del maíz. En Trujillo, Miranda y de la Hoz (2018), presentan el codo, la cuarta, el paso y el pie como medidas autóctonas utilizadas para establecer distancias entre los surcos y las matas que siembran. Mientras que en la siembra de café, se emplean la vara, la braza y la vara grande para organizar la siembra, de modo que las matas queden alineadas facilitando así la recolección de la cosecha.
En la gastronomía y la agricultura, Rodríguez-Nieto et al. (2019), reportaron los procesos de medición en la elaboración del bollo de yuca, donde un campesino empaca y transporta la yuca, usando unidades de medida no convencionales como el saco, el bulto y el tercio. En otras investigaciones se consideran unidades y patrones de medida como la vara y la braza que equivalen a dos metros, y el paso (tranco) es igual a un metro (Rodríguez-Nieto, 2020). Asimismo, los contextos relacionados con la distribución de suelos para sembrados de café o la delimitación de propiedades, favorecen la comprensión de conceptos geométricos como área y perímetro (González, Santa & Londoño, 2014; Toledo & Cruz, 2018).
Cabe destacar que, en el primer periodo evolutivo antropométrico de las nociones metrológicas del hombre, se consideraron las unidades básicas de las medidas asociadas al cuerpo humano, y posteriormente el hombre busca sus unidades de medición en su entorno, como los objetos (Kula, 1980). De este modo, para Kula (1980), la creación de una medida: “requiere de una actividad mental muy compleja y se basa en la medición abstracta de una de las características propias de unos objetos y la comparación de estos en base a aquella”.
Para Godino, Batanero y Roa (2002), la medición “procede secuencialmente desde la percepción a la comparación y después a la aplicación de un estándar de medida (o referente)” y definen la unidad de medida como la cantidad usada como elemento de comparación reiterada (Godino et al., 2002). Sin embargo, García y Osorio (2008), señalan que ver a la medida como un proceso de asignación numérica, implica obstáculos en su aprendizaje. Para la Real Academia Española (RAE, 2018), medir es comparar una cantidad con su respectiva unidad de medida, con el fin de hallar cuántas veces la segunda está contenida en la primera.
Desde la óptica Etnomatemática, existen investigaciones interesadas en el análisis de patrones en diversas prácticas culturales (Gerdes, 2013; Muhtadi, Sukirwan, Warsito & Prahmana, 2017). La noción de patrón se vincula con: ritmo, simetría, secuencia, repetición, dimensión, iteración, y se presenta en cualquier contexto. Devlin (1998), define las matemáticas como la ciencia de los patrones abstractos, esencia del pensamiento, comunicación, cálculo, sociedad, y simplemente la vida. Con base en esta definición, Kraft (2004) señala que los patrones pueden establecer conexiones entre lo cultural y las ciencias naturales. Así, en el contexto cultural, un patrón consta regularmente de unidades repetidas cuya repetición es posible en todas las dimensiones y potencialmente infinito.
Gerdes (2013), clasificó patrones geométricos emergentes de grupos indígenas, afrodescendientes y otros; a partir de ellos generó una tipología de patrones (planares, entrecruzados, de colores, decorativos). Aroca (2008; 2013), distingue dos tipos de patrones: figurales y geométricos, y su vinculación con el pensamiento matemático. Por ejemplo, Aroca (2008) señala la incidencia del pensamiento geométrico en la práctica del tejido de las mochilas de la comunidad indígena de los arhuacos. El patrón figural es el conjunto de trazos mínimos y visibles de la figura tradicional que permite, por medio de algunas transformaciones geométricas, generar la figura en su totalidad. Además, Aroca (2015), indagó sobre los patrones figurales, movimientos y transformaciones en el círculo, triángulos, ángulos, figuras zoomorfas o antropomorfas, anillos, sectores circulares y simetrías, la homotecia, superficies cóncavas, y traslaciones.
En este sentido, el patrón figural es una representación de una figura visible configurada que cumple con características geométricas, mientras que el patrón geométrico, que no es estrictamente mental, es la estructura del patrón figural, es el lenguaje formal que subyace a él (Aroca, 2008). El patrón geométrico es la abstracción y la visualización del proceso espacial repetible (Kraft, 2004), utilizados en diferentes comunidades (africanas, indígenas, entre otras) y, sus diseños son comunes para el tejido de mochilas, canastos, sombreros, máscaras, que además de tener su valor estético, también poseen significados dentro de sus creencias (Valencia-Salas et al., 2014).
En otros contextos, se han utilizado patrones de medición (Rey & Aroca, 2011; De La Hoz et al., 2017; Rodríguez-Nieto, 2020). Rey y Aroca (2011), encontraron patrones de medición como la cuarta, cuyo patrón de referencia es la mano, así como objetos de referencia, como una cuerda, donde su longitud sirve como patrón de medida. De la Hoz et al. (2017), identificaron que la vara es equivalente a la distancia que hay desde la punta del dedo índice de una persona hasta la parte central de su pecho, usado como patrón de medición de los Arhuacos. Rodríguez-Nieto (2020), identificó patrones de medición como “la pita” y “el palito”, en la elaboración de cometas y cajones y, “la vara” para medir la distancia entre una planta y otra. En esta línea, Godino et al. (2002), asumen que:
La imposibilidad o dificultad de trasladar la colección o el objeto en cuestión en el espacio o en el tiempo, debido al tamaño o naturaleza de estos, lleva a tomar un objeto (o varios) de referencia que sí se pueden trasladar o reproducir. Dichos objetos de referencia son las unidades o patrones de medida.
El patrón de medida hace referencia a la unidad básica. Es el hecho aislado y conocido que sirve como fundamento para crear una unidad de medir magnitudes. Los lineamientos curriculares del Ministerio de Educación Nacional de Colombia (MEN, 2006), señalan que, este tipo de patrón desarrolla el sentido de la medida e involucra significativamente aspectos geométricos como la semejanza en mediciones indirectas y aspectos aritméticos fundamentalmente, implicando el desarrollo del pensamiento métrico.
La revisión anterior permite identificar que las investigaciones valoran el conocimiento de nuestros antepasados o ancestrales (e.g., medidas no convencionales), inmerso en prácticas cotidianas relacionadas con: el sector agrícola, la pesca, elaboración de cometas, cajones, bollos de yuca, siembra de café, maíz, yuca, guandú, construcciones de casas, así como la posible vinculación de los conocimientos matemáticos de culturas en el currículo escolar o planes de estudio. Si bien existen investigaciones sobre patrones de medida en la creación de artefactos y siembras, en la práctica cotidiana de la siembra de palma de coco (Cocos nucifera L.), de interés en esta investigación, no se ha reportado un estudio dirigido a la enseñanza y aprendizaje de las matemáticas.
En el caso de la palma de coco, se han adelantado estudios sobre el rendimiento de la copra del coco y los sistemas de producción (Lagunes-Fortiz et al., 2021). En Yucatán-México, Uzcanga et al. (2015), analizaron las preferencias de los consumidores hacia tres derivados alternativos del cocotero: tuba, aceite y agua de coco, encontrándo que la comida con aceite de coco es más sabrosa. En el mismo contexto geográfico, Ramos et al. (2021), indagaron sobre la recuperación de la producción de cocos, encontrando que: “es importante la creación de vínculos entre productores, académicos y gobierno, dar capacitación sobre el aprovechamiento integral del fruto e impulsar políticas públicas para minimizar las debilidades de la cadena de producción y maximizar las oportunidades para los productores”.
En este sentido, sería fundamental investigar y vincular los procesos de siembra, producción y comercialización, para favorecer la enseñanza y aprendizaje de las matemáticas. Esto lo refuerzan Martínez-Padrón et al. (2019), al afirmar que en dichas prácticas agrícolas subyacen contenidos aritméticos, geométricos y algebraicos, al momento de contar, medir o diseñar, donde pueden aparecer formas, patrones y maneras específicas de razonar. Por ello, en este artículo nos proponemos identificar y conectar medidas y patrones en tipos de siembra de palma de coco, construidos por un campesino mexicano.
2. Metodología
Esta investigación es cualitativa enmarcada en la etnografía (Hernández, Fernández & Baptista, 2014), desarrollada en tres etapas: i) selección del participante y conversaciones de acuerdos entre él y los investigadores sobre su rol en la participación. ii) implementación de una entrevista semiestructurada para recolectar los datos y explorar la práctica cotidiana. iii) análisis temático de datos (Braun & Clarke, 2006).
2.1 Participante y contexto
Un campesino-comerciante del suroeste de México participó en esta investigación de manera voluntaria. Él nació en Técpan de Galeana, Guerrero, vivió su niñez junto con sus abuelos y padres, quienes construyeron una huerta de palmas de coco. Sin embargo, hace mucho tiempo reside en la capital (Chilpancingo de los Bravo) con su familia. Actualmente, tiene 64 años y dedicado a la siembra de palmas de coco durante 50 años. Además, su pasión por el campesinado lo llevó a formarse académicamente como licenciado en agronomía y profundizar en aspectos de las ciencias biológicas, químicas y matemáticas.
2.2 Recolección de datos
Los datos fueron recolectados en dos momentos basados en el método etnográfico, porque la etnografía permite que el etnógrafo comprenda y se apropie de la cultura de las personas y reporte los sucesos tal y como se presentan en la realidad (Restrepo, 2016). El primero fue la familiarización con el participante llegando a un acuerdo, es decir se le comentó que se estaba realizando un proyecto de investigación sobre las matemáticas inmersas en prácticas cotidianas desarrolladas por comerciantes y artesanos de Chilpancingo. El participante decidió colaborar, lo que significó emprender un viaje de relación amena de diálogo y exploración entre los investigadores y el comerciante. El segundo momento, dirigido a conocer la práctica del sembrado de cocos, llevó a implementar una entrevista semiestructurada (Hernández et al., 2014) iniciada con la pregunta: ¿Cómo inicia y en qué consiste la siembra de cocos?. A partir de esa pregunta surgió información que le permitió a los autores seguir una conversación rica y puntual sobre la práctica; es decir, con base en las respuestas del participante, el entrevistador formulaba nuevas preguntas para profundizar en el tema. D’Ambrosio y Knijnik (2020), afirman que, “la mayor parte de la investigación en etnomatemática implica llevar a cabo un trabajo de campo en el que se utilizan técnicas etnográficas, como la observación participante, la grabación de audio, el diario de campo y la entrevista”.
No obstante, el trabajo de campo (entrevista) con el campesino no se realizó en la huerta, sino en su casa por motivos de la covid-19. Por tal razón, las evidencias se videograbaron en la sala de su casa (siguiendo las medidas de seguridad: uso de cubrebocas y distanciamiento social), también se enfatizó en los dibujos para dar una idea visual y artística de la huerta y los sistemas de siembra. Además, algunas producciones escritas en Portable Document Format (PDF) fueron compartidas vía WhatsApp. Después de tomar los datos sobre la siembra de cocos, se procedió a su análisis.
2.3 Análisis de datos
El análisis de datos se llevó a cabo siguiendo las seis fases de análisis temático sugeridas por Braun y Clarke (2006) (ver Figura 1, de elaboración propia a partir de los autores mencionados), quienes sostienen que este tipo de análisis permite al investigador identificar, analizar y reportar patrones (temas) dentro de los datos, así como organizar y describir detalladamente un conjunto de datos. Asimismo, se mantuvo la idea de D’Ambrosio (2014), y D’Ambrosio y Knijnik (2020), con relación a las investigaciones basadas en el Programa Etnomatemática, donde se pueden observar las prácticas de diferentes grupos culturales, seguidas de un análisis de lo que hacen y por qué lo hacen. También se siguió el principio de análisis de prácticas cotidianas como se hizo en Rodríguez-Nieto et al. (2019), lo cual coincide con la fase del reporte de los resultados de Braun y Clarke (2006).
Para ilustrar lo anterior, se presenta un ejemplo de análisis de datos etiquetando al investigador (I) y el participante (P), ver el extracto de la transcripción siguiente:
I: Y ¿Dado el caso que no hubiese tenido una cinta?
P: Se puede medir con un cordel, con los pasos, un metro normalmente es un paso, sino tuviera cinta, por ejemplo, este es un metro (señala la medida desde su pecho hasta el dedo).
En el extracto de entrevista (transcrito) se evidencian palabras clave o códigos como cinta, cordel, pasos y metro que sugieren unidades de medidas de longitud, y, frases que soportan las conversiones y equivalencias (e.g., un metro normalmente es un paso). Ahora bien, estos códigos tienen características similares por ser unidades de medida de longitud, en referencia al tema. Posteriormente, los investigadores revisaron los temas y por último hicieron un reporte de los resultados, como se presenta en la sección 3.
3. Resultados y discusión
3.1 Resultados
En este apartado se presentan los hallazgos correspondientes a medidas y patrones evidenciados en los sistemas de siembra (marco real y tres bolillos), de palma de coco (ver Figura 2), usados por un campesino mexicano.
Medidas y patrones en el sistema de siembra Marco Real
En el proceso de siembra de palmas de coco basado en el sistema marco real, se identificaron unidades de medidas convencionales, no convencionales y patrones de medidas y figurales. Inicialmente el campesino describió a la hectárea, equivalente a diez mil metros cuadrados, como unidad de medida para la superficie de siembra. En este caso el campesino se centró en la hectárea equivalente a cien metros por cien metros (ver extracto de la transcripción).
I: Cuando son cantidades de matas (plantas), el espacio ¿Cómo lo distribuye?
P: ¡Ah! la distancia, vamos a suponer aquí vamos a hacer cien metros, cien metros…
I: ¿Qué es eso? (Con base en el dibujo, I preguntó).
P: Son las líneas donde van a ir las palmas, aquí son cien metros, vamos a hablar de una hectárea de tierra tiene diez mil metros cuadrados puede ser de cualquier dimensión de largo y de ancho, pero que dé diez mil metros cuadrados, puede ser una longitud de doscientos por cincuenta, pero aquí yo lo voy a hacer de cien por cien, una hectárea.
Posteriormente, el campesino usa diferentes unidades de medida para medir el terreno y ubicar las plantas. En este proceso el campesino usa la cinta métrica de treinta metros para marcar el lugar donde hará los hoyos (separados a una distancia de diez metros), y donde se siembran los cocos. Después la misma cinta métrica la traslada para marcar el lugar donde se harán otros tres hoyos y, por último, para completar el surco de noventa metros, traslada nuevamente la cinta métrica para colocar la marca y realizar diez hoyos. De esta manera, el campesino realiza las marcas para los demás surcos (ver extracto de la transcripción).
P: Con una cinta de medir, hay una cinta que viene de treinta metros que son tres (hoyos separados a una distancia de treinta), y ahí te vas con la cinta, vas marcando, donde se va a hacer el hoyo con una palita.
Otro tipo de unidad de medida usada por el campesino es el cordel o mecate, dividido en distancias de un metro, que el campesino considera equivalente a la medida “desde el lado derecho del pecho hasta la punta del dedo”, haciendo un nudo en el cordel por cada metro, hasta completar diez metros. (ver extracto de la transcripción y Figura 3).
I: ¿Dado el caso que no hubiese tenido una cinta?
P: Se puede medir con un cordel, con los pasos, un metro normalmente es un paso, sino tuviera cinta, con un…, por ejemplo, este es un metro (señala la medida desde su pecho hasta el dedo) que es desde mi lado derecho del pecho hasta la punta del dedo es un metro, yo siempre lo tengo calculado, o también un paso, entonces puede hacerse aquí así (señala la medida desde su pecho hasta el dedo) y con una cinta se hacen nudos a la cinta que vayan dando la misma distancia.
I: ¿Tiene alguna cinta?
P: Aquí es un metro, si tú tienes una cuerda, un cordel, tú le vas haciendo un nudito.
I: ¿Qué pasa con ese nudo?
P: Ahí es un metro, luego, otro metro sería así (ver Figura 3), o también así para que sea más exacta o que no falle.
I: ¿A qué se refiere que no falle?
P: Bueno porque, aquí es más exacto que… aquí le haces el nudito, y sería un metro, en cada nudito es un metro y así te vas con el cordel haciéndole nuditos. Este cordel lo amarras en una estaca y lo estiras, te alineas con la otra estaca que está en el otro extremo, y con base en los nuditos ahí son un metro, marcas los diez metros y los marcas con un botecito con cal.
La otra unidad de medida es el paso, equivalente a un metro y a la medida “desde el lado derecho del pecho hasta la punta del dedo”. Generalmente, el paso es usado cuando se amarra un cordel en una estaca, situada en un extremo del terreno para conservar la línea recta hasta el otro extremo (opuesto) del terreno. Posteriormente, el campesino marca un hoyo cada diez pasos sobre la línea recta establecida con el cordel (ver extracto de la transcripción y Figura 4).
I: Y eso que me decía de los pasos ¿Cómo es?
P: Ah… los pasos son uno, dos, tres… amarras el cordel primero ponen una estaquita allá y otra allá en los cien metros y lo estiras, ahí lo amarras así bien estiradito y ya que lo tienes amarrado vas marcando los pasos uno, dos, tres, … diez pasos, el cordel es para que salga la línea recta y ya las medidas con los pasos, diez pasos son diez metros, le pones otra marca de cal y así te vas.
P: A los diez pasos le pones la cal para que tu sepas que ahí va el hoyo, ese es cuando no tienes una cinta.
I: ¿Cómo les llaman a las líneas?
P: Surcos y al espacio que hay entre surco y surco se le llama camellón.
Otros conocimientos matemáticos se evidenciaron en el diseño y construcción del sistema de siembra marco real. Debido a que no se pudo ir a la huerta del campesino, se logró capturar una vista satelital de la huerta, ubicada en Tecpan de Galeana, por medio de Google Maps (ver extracto de la transcripción y Figura 5).
P: Ahora para el diseño de la siembra, estas son las líneas (las cuenta (10)).
I: Preferiblemente, son diez líneas.
P: Se pueden sembrar a una distancia de diez metros, diez por diez en cuadro.
I: ¿A qué se refiere en cuadro?
P: Así, por ejemplo, uno, dos, tres, cuatro, …, nueve y diez, las palmitas, los pozos van a ir aquí ese es un cuadro, o también se pueden sembrar en triángulo.
Por otra parte, el campesino utiliza el estadal para medir terrenos con más de diez hectáreas. Este instrumento es usado por los topógrafos y está constituido por la dupla prisma-estación para distancias y alturas (ver extracto de la transcripción).
I: ¿Con qué miden esos metros?
P: Pues con cinta, cuando son extensiones grandes, pues con aparato topográfico se ponen los tripies (trípodes), y con el aparato se va marcando, con un estadal un palito así se pone el aparato y se ve y ya el estadal donde pegue la vertical y ahí va… es rápido.
I: Y ¿Siempre han utilizado el estadal?
P: No, no, esa es una técnica más sofisticada, ahorita una persona que quiera sembrar diez, veinte, treinta, cien hectáreas que esté terreno plano, le es más fácil con un aparato (estadal), pero una, dos o tres hectáreas pues lo puede hacer con cinta o con un cordel, un mecate.
En la Tabla 1 se presenta el sistema de medidas usado por el campesino en la siembra de coco en Tecpan de Galeana.
Tabla 1. Unidades de medida en la siembra con Marco Real.
| Tipo | Nombre | No convencional | Convencional |
|---|---|---|---|
| Longitud | Cordel o mecate | x | |
| Paso | x | ||
| Camellón | x | ||
| Brazada | x | ||
| Longitud desde la punta del dedo hasta el pecho. | x | ||
| Cinta métrica | x | ||
| Metro | x | ||
| Estadal | x | ||
| Superficie | Hectárea | x |
Después de marcar y medir la superficie de siembra, el campesino procede a hacer los hoyos para sembrar los cocos, o bien, las palmitas. Estos hoyos tienen forma de cubo con medidas de treinta centímetros de largo, treinta centímetros de ancho y treinta centímetros de alto, evidenciándose medidas volumétricas y figuras tridimensionales como el cubo. Cabe destacar que la forma del hoyo se repite en todas las marcas realizadas.
I: ¿Cómo es el proceso de sembrado de la palma de coco?
P: El fruto que es el coco, de ahí germina una palmita y esta se trasplanta en la tierra en un hoyito de medio metro o puede ser treinta de largo por treinta de ancho y treinta de alto.
I: ¿Cómo haría un dibujo de los treinta centímetros donde introduce el coco?
P: Si… se hace, este es el suelo, la tierra, entonces aquí se… puede ser de treinta a cuarenta centímetros, de treinta a cincuenta centímetros de ancho y aquí igual.
I: Entonces ¿Usted cómo le llamaría al espacio (I señala el dibujo)?
P: El hoyo o pozo.
I: ¿Qué forma tiene ese pozo?
P: Es cuadrado o redondo, o sea, donde quepa el coco nada más, no es necesario hacerlo muy amplio.
I: Pero preferiblemente ¿Cómo?
P: Así como está ahí cuadrado (señala el dibujo), sí, porque aquí se entierra y en caso de que se riegue aquí queda el agua y penetra aquí la tierra (ver Figura 6).
En la Figura 6 se evidencia una conexión etnomatemática desde la perspectiva de Rodríguez-Nieto (2021), que relaciona la forma del hoyo para sembrar el coco con el concepto matemático “cubo”, que tiene tres dimensiones iguales (largo=ancho=alto= 30 cm). Es decir, se establece una relación entre la matemática identificada en la práctica cotidiana y la matemática institucionalizada, universal o pública que se aborda en los planes de estudio, libros de texto, etc. A su vez, el hoyo o cubo funciona como patrón ya que se repite, conservando su diseño y medidas para plantar todas las palmas de coco, y tiene como volumen: V=largo∗alto∗ancho=30cm∗30cm∗30cm=27.000c m 3 .
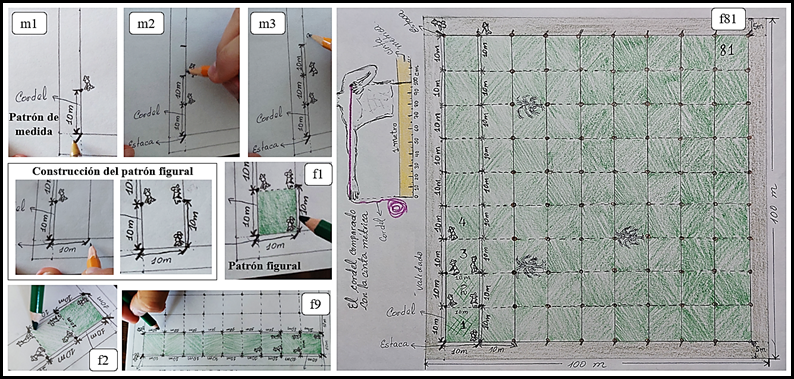
Para la construcción del sistema de siembra marco real, se identificaron patrones de medida y figurales conectados con las medidas usadas por el campesino. En este contexto, el campesino usa tres patrones de medida: la cinta métrica, el cordel y el paso, que le permiten reconocer sus unidades de medida o referencias (10 metros) para medir el terreno, reproducir y conservar dicha medida. Este proceso se realiza para marcar la distancia entre las palmas ubicadas en un mismo surco. Además, el campesino utiliza este patrón de medida para hallar la distancia entre dos o más surcos, lo cual lleva a la conformación de un cuadrado que se repite iteradamente hasta generar un camellón. El cuadrado formado, es el patrón figural que se va construyendo a medida que el campesino siembra sus palmas (ver Tabla 2). En particular, el patrón de medida “metro” se puede usar por medio de una cinta métrica, pero el campesino generalmente establece equivalencias para el metro como “el cordel” y “el paso”. En el caso del cordel, el campesino establece una distancia de un metro y coloca un nudo, el cual reproduce a través de la comparación reiterada hasta conseguir los 10 metros. Este mismo proceso se evidenció cuando el campesino usó el paso como su patrón de medida, es decir, 10 pasos equivalen a 10 metros (ver Tabla 2).
Tabla 2 Patrones identificados en la siembra de Marco Real.
| Descripción | |
|---|---|
| Patrón de Medida | Patrón de medida convencional
|
| Patrón de medida no convencional
| |
| Patrón figural | El cuadrado con área de 100 m 2 es un patrón figural que se repite con regularidad 81 veces en el terreno de siembra, para mantener distancias con medidas iguales entre las palmas de coco. |
En la Figura 7 se representan los patrones descritos en la Tabla 2 y se especifican los patrones de medida por momentos (m1, m2, m3, …) y los patrones figurales representados por figuras (f1, f2, …, f81), en el sistema de siembra marco real. Es decir, en la Figura 7, el momento 1 (m1) significa que el campesino realiza su primera medida equivalente a 10 metros referido al patrón de medida (cordel) que se reproduce hasta en los momentos siguientes para construir todo el sistema de siembra. Mientras que f1, f2, …, f81, significa la representación de los patrones figurales con forma de cuadrado desde la construcción de los patrones de medida, lo cual evidencia la conexión: patrón de medida - patrón figural.
Medidas y patrones en el sistema de siembra Tres Bolillos
Este sistema de siembra se caracteriza por requerir más conocimientos matemáticos para su conformación y por el aumento de la cantidad de plantas que pueden caber en una hectárea, a diferencia del sistema marco real. En este sentido, el campesino manifestó que la ubicación de las plantas de coco forma un triángulo equilátero (ver extracto de la transcripción).
P: […] el sistema de tres bolillos va una planta de palma en la parte de la arista, en cada punta del triángulo. Y eso es efectivamente un triángulo equilátero que se forma.
I: Y, ¿Por qué es equilátero?
P: Es equilátero. Debe ser por ejemplo si son 9 metros por 9 metros por 9 metros. Aquí la diferencia con el marco real es de qué una palma queda en medio de dos. O sea, forman un triángulo equilátero. Van a ser 4 en marco real, serían tres en triángulo […]
Posteriormente, el campesino dibujó una parte del sistema de siembra, mostrando la ubicación del triángulo equilátero en el terreno y cómo encuentra la distancia entre surcos, que es la línea desde un vértice del triángulo hasta la mitad de la base (ver extracto de la transcripción y Figura 8).
P: Sí. Entonces, se tiene la base de nueve metros hacia abajo, nueve metros hacia arriba, un triángulo equilátero, entonces de la parte de arriba de una arista trazo una línea hacia abajo, hacia la mitad del lado de la base … Esta va a ser la distancia entre surcos.
En la Figura 8 se muestran otros aspectos matemáticos desencadenados cuando el entrevistador le preguntó al campesino ¿Cuánto es esa distancia?, a lo cual respondió el campesino “es lo desconocido” y, para encontrarlo, el campesino describió que primero tiene en cuenta que la suma de los ángulos internos de un triángulo es igual a 180° y al ser el triángulo equilátero, los tres ángulos miden 60°. Posteriormente, usa dos métodos para encontrar la distancia entre surcos: En el primero halla la mitad del ángulo de 60° que es igual a 30° y toma como cateto opuesto la base de 4.5 metros, la hipotenusa de 9 metros y el cateto adyacente es el desconocido. Con esta información acudió a la razón trigonométrica cos B = cateto adyacente hipotenusa , para hallar la medida de la distancia entre surcos (ver extracto de la transcripción y Figura 8).
P: Entonces efectivamente para calcular esa distancia entre surcos, ahí sería con el teorema de Pitágoras, sería un triángulo rectángulo, sería entonces los ángulos de arriba como miden 60 grados, la mitad son 30 … entonces para tomar el cateto opuesto sería el de la base, la mitad de nueve sería 4.5 metros … y la hipotenusa sería 9 metros. Se desconoce el cateto adyacente en este caso, porque el ángulo el de arriba, el de 30 grados, entonces sería por el coseno, porque el seno de 30 grados sería cateto opuesto sobre hipotenusa y el coseno es cateto adyacente sobre hipotenusa. Entonces la distancia entre surcos vendría siendo el cateto adyacente del coseno de 30 grados, entonces es lo que se desconoce.
En el segundo método, propone que se puede usar el teorema de Pitágoras porque tiene la hipotenusa (c = 9 metros) y un cateto (b = 4.5 metros) del triángulo rectángulo ABC (ver extracto de la transcripción y la Figura 9).
I: ¿Cómo lo calcula?
P: Aquí hay una fórmula, es cateto opuesto al cuadrado más el cateto adyacente al cuadrado es igual a la hipotenusa al cuadrado.
En la construcción del sistema de siembra tres bolillos, el campesino evidenció el uso de patrones de medidas y con estos conformó los patrones figurales. Cabe destacar que, estos patrones de medidas son los mismos identificados en el sistema marco real (la cinta métrica, el cordel y el paso), evidenciándose una conexión externa desde la perspectiva de Rodríguez-Nieto (2020), pero cambia en su forma de uso. Por ejemplo, la distancia entre palmas de coco ubicadas en un mismo surco es igual a nueve metros (patrón de medida) y para medir los nueve metros usa la cinta métrica, el cordel o el paso de manera reiterada. No obstante, el campesino menciona que, después de medir los nueve metros requiere hallar la distancia entre surcos (camellón) que corresponde a la medida de la altura de un triángulo equilátero (7.79 metros). En este aspecto, se reconocen dos patrones de medida convencionales, uno para la distancia de la base del triángulo y el otro para la altura, que es necesario para trazar otros surcos y formar camellones (ver Tabla 3). El triángulo formado en la siembra tres bolillos, se reconoce como el patrón figural de este sistema, el cual genera mayor trabajo para el campesino, pero mayor cantidad de plantas sembradas en el terreno de una hectárea. Este patrón desde la literatura es de tipo figural de reproducción (Rivera & Sánchez, 2015).
Tabla 3. Patrones identificados en el sistema de tres bolillos.
En la Figura 10 se representan los patrones de medida y figurales y su conexión con las medidas (convencionales y no convencionales), usadas por el campesino en el sistema de siembra tres bolillos. Cabe destacar que el triángulo equilátero es el patrón figural de reproducción, que se itera 204 veces en el terreno de siembra basado en la medida del cordel equivalente a 9 metros. En la Figura 10, se evidencian los patrones descritos en la Tabla 3 y se especifican los patrones de medida por momentos (m1, m2, m3, …), en términos de cada medida de 9 m, y los patrones figurales representados por figuras triangulares (f1, f2, …, f204).
3.2 Discusión
En esta investigación se identificaron las medidas y patrones conectados entre sí, usados por un campesino en la construcción de dos sistemas de siembra de palmas de coco. Los resultados de este trabajo muestran el potencial matemático del campesino, debido a que en la mayoría de la explicación de su práctica cotidiana usó nociones matemáticas, por ejemplo, en la siembra marco real, se refirió al cuadrado, línea recta, hectárea, centímetros, metros, área, caja (cubo), entre otros. En el sistema de tres bolillos, usó: el triángulo equilátero, triángulo rectángulo, ángulo recto, rectas perpendiculares y paralelas, punto medio, operaciones aritméticas, hexágono, rombo, el teorema de Pitágoras (haciendo alusión a los catetos opuesto, adyacente, e hipotenusa de un triángulo rectángulo), distancia, razones trigonométricas como el seno, coseno y tangente. Además, el campesino reconoció la propiedad de los triángulos, cuando dijo que “la medida de los ángulos internos de un triángulo es igual a 180°”. Reconocemos que, el campesino tiene un amplio conocimiento matemático que le ayuda en su labor de siembra, lo cual tiene sentido por su formación profesional como agrónomo y experiencia en el campo.
Los resultados de esta investigación aportan a la amplia literatura en Educación Matemática y al Programa Etnomatemática, en cuatro direcciones. Primero, se indagó sobre dos sistemas de siembra que no se habían explorado anteriormente en otras investigaciones enfocadas en la agricultura y siembras (De la Hoz et al., 2017; González et al., 2014; Toledo & Cruz, 2018; Rodríguez-Nieto, 2020; Trujillo et al., 2018). Segundo, se analizaron medidas convencionales y no convencionales de longitud y su conexión con patrones de medida y figurales. En la literatura se había informado sobre medidas y patrones de manera separada, los cuales guardan similitudes. Tercero, se ofrece una metodología siguiendo un análisis temático con una mirada etnomatemática, que permitió identificar códigos o frases en el discurso del campesino, sobre medidas y patrones. Otro aporte metodológico, es el papel fundamental de los dibujos hechos por el campesino (Figuras 5, 6, 8 y 9), que expresan su realidad cotidiana. Estos dibujos se unen a los hechos por los investigadores, para expandir y adecuar los sistemas de siembra en un terreno con superficie de una hectárea, que requirieron de una validación por el campesino (Figuras 7 y 10).
En la cuarta dirección, este artículo está dirigido a la docencia de la matemática, ya que el profesor podría usar los conocimientos matemáticos explorados en este artículo, para desarrollar clases sobre: triángulos, mediciones, trigonometría, patrones y usar el geoplano, entre otros, en distintos niveles escolares. Ejemplo de ello es el trabajo de Sunzuma y Maharaj (2020), quienes integraron enfoques etnomatemáticos para la enseñanza de la geometría. Lo anterior es importante ya que en diversos currículos la medición y los patrones son relevantes, pues se demanda que los estudiantes identifiquen y analicen patrones para detectar regularidades (MEN, 2006; NCTM, 2000; SEP, 2017). Asimismo, la medición debe desarrollarse a partir de situaciones cotidianas, de hecho, en el MEN (2006), se propone que a partir de la cotidianidad: “se construye sentido y significado para las actividades y los contenidos matemáticos; y, por lo tanto, es desde donde se establecen conexiones con la vida cotidiana de los estudiantes y sus familias”.
4. Conclusiones
En la investigación se evidenciaron los procesos matemáticos que caracterizan las conexiones entre las medidas y patrones, con la finalidad de no percibirlos o utilizarlos de manera aislada. En el contexto de los sistemas de siembra de palma de coco, se reconoció el potencial matemático asociado especialmente a los patrones de medida, como: la cinta métrica (30 metros), el cordel o mecate, el paso y la brazada, así como patrones figurales que se refieren a cuadrados y triángulos, que se repiten con regularidad en la construcción de los distintos tipos de siembras. Asimismo, se identificó un insumo fundamental para el abordaje de la geometría y la trigonometría en el aula de clases de matemáticas, que permite a su vez, la valoración de las matemáticas implícitas en el contexto sociocultural de los estudiantes y profesores.
Como futuras investigaciones proponemos que se diseñen tareas matemáticas que involucren problemas sobre medidas (convencionales y no convencionales), y patrones (de medida y figurales), relacionadas con situaciones de la vida cotidiana para promover las conexiones, que son útiles en la comprensión de conceptos matemáticos.