INTRODUCTION
To Robert Hermann (1931-2020)
Beginning in the second half of the 20th century, some philosophers of mathematics have advocated a more 'practice oriented’ approach to their field and have developed what is now called the philosophy of mathematical practice. This intellectual movement argues that restricting philosophy of mathematics to foundationalism and logicism not only caricatures the production of mathematical knowledge, but also overlooks important philosophical questions that would benefit from being investigated through the study of praxis. Mancosu (2008), one of the main proponents of this approach, stated at the end of the 2000s that:
Attention to mathematical practice is a necessary condition for a renewal of the philosophy of mathematics. We are not simply proposing new topics for investigation but are also making the claim that these topics cannot effectively be addressed without extending the range of mathematical practice one needs to look at when engaged in this kind of philosophical work. Certain philosophical problems become salient only when the appropriate area of mathematics is taken into consideration (p. 2).
Although the epistemic stance that accepts mathematical practice as relevant to philosophical inquiries has its roots in the mid-twentieth century, the number of contributions has only flourished in the last twenty years. Indeed, the impressive outpouring of papers, monographs, conferences, and collective volumes, as well as the creation of the Association for the Philosophy of Mathematical Practice in 2009, affirm the position of the philosophy of mathematical practice as a legitimate subfield of the philosophy of mathematics.1
However, although philosophers of mathematical practice advocate a philosophical approach that interacts with other disciplines, the integration of sociological concepts and methods has been scarce. This may be explained by the embryonic state of the sociology of mathematics, despite early works by sociologists Bloor (1973, 1976) and Restivo (1988), and some recent but scattered contributions (MacKenzie, 1999; Heintz, 2000; Rosental, 2008; Zarca, 2012). It seems to us that this lack of recognition of sociology in the philosophy of mathematical practice is partly due to a cognitive-oriented stance that is prevalent among philosophers of mathematics. Indeed, in the last twenty years, numerous publications have addressed the relationship between cognitive sciences and mathematical knowledge (Netz, 1999; Lakoff & Núñez, 2001; Leng et al., 2007; Pease et al., 2013; Bangu, 2018). A recent monograph notes this trend in the philosophy of mathematical practice, which favors a cognitive and agent-based approach (Ferreirós, 2016). In comparison, little has been done to integrate sociological approaches with the philosophy of mathematical practice, even where it would seem legitimate.
This article highlights how the philosophy of mathematical practice would benefit from a sociological perspective. For instance, sociological concepts such as scientific communities are of central importance for understanding collective mathematical practices. Based on the literature in the sociology of science, a community-centered approach to the study of mathematical practice will be advocated first. It will then be explained how this approach is particularly suited to outline the role of metamathematics, a philosophical concept used as placeholder for the opinions, views and positions which mathematicians maintain with respect to their practice (Kitcher, 1984). It has been considered that change in metamathematics is often associated with ‘revolutionary’ changes in mathematics (Dunmore, 1995), as exemplified by the emergence of modern algebra at the beginning of the 20th century (Corry, 2004). In contrast, much less has been said on the role of metamathematics in stabilized mathematical practices. The emergence of geometric control theory, and one of the founding theorems of this community: the orbit theorem, will be used as a case study to show the need to connect the notion of metamathematics to that of scientific communities.
In the first part of the case study, it is shown how that the introduction of geometric tools in control theory in the 1960s precipitated a change in the metamathematical perspective, resulting in the emergence and grow of a new practice. This mathematical community - later called ‘geometric control theory’ - has the particularity of merging elements from differential geometry and from applied mathematics to solve problems about systems of nonlinear differential equations. A founding element of this community is the so-called orbit theorem: although this label only appeared in the 1980s, it refers to a statement originally formulated - and proved independently - by control theorist Sussmann (1973b) and differential geometer Stefan (1974b). Although the content of their respective contributions is quasi-identical, it appears that their presentations differ in a way that parallels their respective disciplinary affiliation. Then, an analysis of contemporary citational practices demonstrates that the identification of the work of Stefan and Sussmann -as well as that of another geometer, Tadashi Nagano - with the label ‘orbit theorem’ is mostly restricted to the community of control theory. The article concludes by discussing how metamathematical views associated to the collective practice of a mathematical community shape the production and the receptions of mathematical knowledge. Relying on both quantitative and qualitative methods, the case study illustrates how sociological perspectives are not only relevant but also fruitful to research in the philosophy of mathematical practice.
MATHEMATICAL COMMUNITIES AND THE INTERPLAY OF THEIR PRACTICES
A sociological approach to mathematical practice
Mathematical research is a collective enterprise ranging from training under the supervision of a mentor, to writing and publishing papers as a professional mathematician. However, these institutional aspects are merely the tip of the iceberg, for knowledge acquisition is mediated through various instances: discussions with colleagues, books, talks, etc., all of which are socially shaped or constrained. Moreover, learning the implicit norms regulating a domain of mathematics and constructing a professional ethos can only be made through the succession of social experiences lived by the mathematicians. Thus, to study mathematical practice, it seems legitimate to adopt a sociologically oriented perspective focusing on communities of researchers.
This position is illustrated by the work of sociologist Rosental (2008). In his monograph, he studies a controversy in logic triggered by the uncertainty surrounding the proof of Elkan’s theorem in the 1990s. The unfolding of the debates among logicians reveals how a theorem is produced by its scientific community and how it is not reducible to a mere cognitive content discussed according to purely individual dynamic. Rosental (2008) emphasizes the collective dimension of the process by which the theorem achieved the status of certified knowledge. His work is a rare attempt of studying the production of theoretical knowledge from an anthropological perspective. In particular, he warns the reader of the danger of invoking the immateriality of logico-mathematical knowledge, that would be exclusively localized in the minds of the scientists. Rather, he argues that a relevant approach to the understanding of scientific practices in logic and mathematics should rely on a social and material analysis of the debates. For example, in his case study, he notices the importance of the role of online forums in giving a collective meaning to Elkan’s statements, by enabling the transmission of theoretical, immaterial arguments. The study of material supports as conveyors of immaterial knowledge has been further investigated in another anthropological study, led by Barany and MacKenzie (2014), in which they provide an ethnographic account of how blackboards structure the exchange of immaterial theoretical knowledge in the mathematics department.
This anthropological approach not only invites us to focus on the material dimensions of scientific research, but also to study mathematical practice at the level of communities of researchers. Following the historian of mathematics Dahan-Dalmedico (1994), Rosental (2008) defends the idea of developing a social history of mathematics, which would not be limited to the history of a concept or the work of an individual, but would rather include “the study of a scientific milieu, a community, a set of scientific productions, in order to apprehend a ‘site’, a geography of works, the emergence of a discipline, and the role of leading academic figures” (p. 37). Barany and MacKenzie support Rosental’s position by observing that the study of mathematical practice relies mostly on historical and philosophical accounts of settled mathematics, thus lacking an adequate sociological treatment of ongoing research (Barany & MacKenzie, 2014). Indeed, although the influence of social factors on scientific production has been widely discussed in the sociology of scientific knowledge - for example see (Knorr-Cetina & Mulkay, 1983; Barnes et al., 1996) - and has found some echoes in the history of mathematics (Bos & Mehrtens, 1977; Gispert, 2000), contributions to the sociology of mathematics have remained scarce.
In the history of mathematics, interest in the role of collective practice and in mathematical communities has attracted more and more attention in the last twenty years. For example, regarding mathematical physics, Warwick (2003) described how local factors impacted the reception of Einstein’s theory of relativity at Cambridge. A recent sociohistorical assessment of the notion of mathematical community is the study led by Gauthier (2007, 2009) on mathematicians working on the geometry of numbers in the first half of the 20th century. Another important account of international collaborative work in mathematics has been made by Barany (2018), on the emergence of Schwartz’ theory of distributions. Finally, a recent collective volume on the institutional and social history of mathematical communities in the interwar period has just been published (Mazliak & Tazzioli, 2021).
However, in the history and the sociology of sciences, the notion of scientific community has generated a large body of literature since the 1960s (Ben-David & Collins, 1966; Kuhn, 1970; Crane, 1972; Mullins, 1972; Edge & Mulkay, 1976; Lemaine et al., 2012; Knorr Cetina, 1999; Frickel & Gross, 2005). These contributions focus either on institutional aspects or on the more social aspects which define scientific communities. For example, in his discontinuous account of scientific change, Kuhn (1970) identifies scientific communities as communities of views, practice and commitments. To each community he associates a paradigm - or a disciplinary matrix in his later work - since this notion should much better reflect its relationship with the scientific community to which it belongs. Kuhn borrowed this perspective from Fleck (1979), who introduced the notions of thought collective (Denkkollektiv) and of thought style (Denkstil). Moreover, he acknowledges the multi-level aspect of scientific communities - smaller specialties inside larger disciplines - and emphasizes that his model should fit this taxonomy (Kuhn, 1977, pp. 296-297).
Although philosophers of mathematics have discussed the relevance of adapting the notion of disciplinary matrix to describe mathematical change (Mehrtens, 1976), they do not seem to have specified how it would be articulated with the multi-level taxonomy of mathematical communities. Except in a few cases (Van Kerkhove & Van Bendegem, 2004), most famous attempts of describing mathematical practice occurred either at the global level (Kitcher, 1984) or at the individual level (Ferreirós, 2016). While it is certainly necessary to study the evolution of mathematicians’ individual practices, a sociological approach would enable to explore practices associated to different communities. This paper adopts the view of a socio-historical perspective on mathematical practice relying on the notion of mathematical community and on their multi-level taxonomy. The notion of metamathematics crafted by the philosophy of mathematics allows to ground practices in the notion of mathematical communities.
The role of metamathematics in mathematics
One of the earliest attempts to assess the validity of Kuhn’s model in describing mathematical change was led by philosopher Mehrtens (1976), who concluded that normal science, anomalies, and crisis occur in mathematics, but that the concept of revolution should be adapted for mathematics. Philosopher Philip Kitcher also defended the idea that Kuhn’s theory would apply to mathematics with minor modifications. In his book The Nature of Mathematical Knowledge, Kitcher (1984) provided a model for mathematical growth along Kuhn’s lines. Kitcher’s idea is to replace the notion of disciplinary matrix by the notion of mathematical practice. It can be described, at a given time, by a set ⟨L, S, R, Q, M⟩ of five components: a language L in use among mathematicians; a set S of accepted statements, propositions and theorems; a set R of accepted reasonings, proofs and arguments which justify the accepted statements; a set Q of mathematical questions considered as important by the community: those questions which are worth asking and answering, and which have variable difficulty and urgency; and finally a set M of metamathematical and methodological views about the character of the proofs, the articulation and the hierarchy of the disciplines, the scope and the nature of mathematics. Most of these views are implicit in the shared knowledge of the mathematical community and get incorporated during the learning process that every young mathematician goes through.
There exists some empirical ground for the notion of metamathematics. Philosophically inspired inquiries have documented the non-explicit aspects of mathematicians’ appraisal of proofs and reasonings in mathematics (Löwe et al., 2010; Inglis & Aberdein, 2015). An empirical survey led by sociologist Zarca (2009, 2012) on (French) mathematicians substantiates the claim that mathematical practice relies on shared but implicit values. His work provides a comprehensive description of the beliefs and opinions of mathematicians on their own field. Zarca mobilizes the notion of ethos to account for the content of these opinions: a professional ethos is a set of dispositions acquired through experience and which depend on what is socially recognized as relevant in the exercise of a profession, in any dimension (epistemic, aesthetic, social, etc.). Dispositions are a central element of Bourdieu’s theory of fields and habitus; they can be considered as embodied and regularized schemes of action and beliefs, internalized through familial and professional socialization (Lahire, 2003, 2019). Zarca (2009) explains that:
A professional ethos can be identified from the individual practice and judgments of the members of the profession, as well as from the collective practices and judgments, crystallized in hierarchies, prestige, or power and objectified in the modes of organization of exchanges, control of work, distinction of excellence, etc. (p. 352).
Mathematicians in training must become acquainted with these implicit hierarchies, rules and norms of behavior that are interwoven with their professional practice. Thus, the sociological notion of ethos sheds light on the process by which mathematicians acquire metamathematical opinions on their practice.
Kitcher (1984) justifies the relevance of his model by arguing that change occurs in mathematics through what he calls interpractice transitions from some mathematical practice ⟨L, S, R, Q, M⟩ to another mathematical practice ⟨L′, S′, R′, Q′, M′⟩. Kitcher (1984) contends that the evolution of mathematics consists of a sequence of mathematical practices and that the role of metamathematics is central in these transitions: "changes in metamathematical views are intertwined with large-scale changes in other components, and metamathematical change serves to indicate those episodes which are the closest analogs to scientific revolutions" (pp. 191-192).
An example of such a ‘revolutionary’ change has been proposed by Corry (2004), who shows that the image of mathematics2 shared by algebraists had changed at the beginning of the 20th century. In particular, the reconfiguration of their metamathematical perspectives led to the emergence of modern algebra and materialized in the publication of Bartel L. Van der Waerden’s textbook Moderne Algebra in 1930. This view is also developed by Dunmore (1995), who considers that profound changes in mathematics may be revolutionary on the meta-level, although still being conservative on the object-level. To explain such changes, Dunmore supports Mehrtens’ claim that anomalies - in Kuhn’s sense - play an important role in revolutionary changes in mathematics: they force mathematicians to modify their metamathematical views to avoid the inconsistencies. Kitcher (1984) contends that it is precisely in such crises in which different views of mathematics compete, and in which mathematicians must commit and defend their views, that metamathematical views become fully explicit (p. 189).
Metamathematics and the interplay of practices
In his book, Kitcher (1984) purported to describe nontrivial changes in mathematical practice. However, his approach suffers from its generality, which prevents his model from accounting for local and specific dynamics, especially those governing the 20th and 21st centuries mathematical production, which is characterized by the professionalization of the discipline. Kitcher’s model of mathematical practice seems to apply to some mathematical community prior to the 20th century, although he acknowledges the existence of several sub-communities, that would be characterized by their own metamathematics. For him, the goals of every mathematical community - such as advancing knowledge, systematizing results, increasing understanding, offering proofs, etc. - “are mediated by more specific metamathematical views, which can vary from community to community, and which represent the community’s reflective understanding about how its ultimate goals are to be achieved" (Kitcher, 1984, p. 189). Unfortunately, Kitcher does not explain how to account for local changes of mathematical practice that would concern only communities of mathematicians.
This is precisely an objection raised by Ferreirós (2016) in his monograph Mathematical Knowledge and the Interplay of Practices. Ferreirós acknowledges the difficulty of accounting for the multi-level structure of mathematical practices and his book is devoted to providing an alternative to what he considers to be reductionist approaches. Among them he includes that of Kitcher, but also its extension by philosophers Van Kerkhove and Van Bendegem (2004), because their model describing the plurality of mathematical practice would be too compartmentalized. Moreover, Ferreirós notices that Kitcher’s adaptation of Kuhn’s model to mathematics promoted an image of the discipline that is governed by a single practice or disciplinary matrix. In contrast, Ferreirós defends the idea that, at a given time, several practices - or frameworks, as he names them - coexist in the mathematical community. While Kitcher, following Kuhn, focuses on interpractice transitions and sees mathematical change as a temporal succession of such practices, Ferreirós is interested in the interactions between practices: what he calls their interplay. For him, practices are interconnected in a systematic fashion at various levels, and the analysis of any practice should require the philosopher to consider the connections with other strata of practices.
The work of sociologist Zarca (2012) lends support to this claim. In his survey, he asked mathematicians to determine the classes of the Mathematics Subject Classification (MSC) to which they believe themselves to belong3: only 36 % of the mathematicians picked up one such class, 27 % chose two, and 37 % chose three. These results reflect the prevalence of interconnections within mathematical specialties. Indeed, the granularity of mathematical communities - which was already recognized as early as the 1960s (Fisher, 1966) - and the widespread lack of co-understanding between mathematicians (Barany & MacKenzie, 2014), are counter-balanced by the high interconnectivity of mathematical sub-domains. This implies that mathematicians may claim membership to various sub-disciplines more often than natural scientists.
For Zarca (2012), the interconnectivity of domains of mathematics plays a tremendous role in the unity of mathematics, even more prominent than the centrality of rigorous demonstrations and axiomatization: “the possibility of solving a problem related to a given discipline by different methods, borrowed from other disciplines, and this, in a reciprocal manner, is a strong sign of the profound unity of mathematics” (p. 233). This has structural implications for mathematical accumulation (compared to the natural sciences): mathematicians do not discard old theories since they are incorporated into the new, more intricated ones, through conceptual connections (Dauben, 1995). Ferreirós (2016) supports this view arguing that:
The whole history of mathematics can be presented as the gradual development of a network of links connecting different core notions that initially lie separate, i.e., as the creation of a delicate tapestry or spider web establishing bridges between the discrete and the continuum, number and geometry, algebra, and analysis-and, later, topology-etcetera (p. 40).
Despite appearing very sensitive to a comunity-centered and a multilevel characterization of mathematical practice, Ferreirós’ (2016) account of the interplay of mathematical practices derives from an agent-based, cognitive approach. For him, the study of mathematical practices should focus on the mathematicians as individuals and on the evolution of their set of metamathematical beliefs through time, as they play a central role in the production of new mathematics and in the reconfiguration of the discipline (pp. 80-82).
There is no denying that every mathematician has an individual history and a unique trajectory in the field: there is so much specialization in mathematics that this is unavoidable. Hence, Ferreirós (2016) is right to emphasize that "a mathematician ENT#091;...ENT#093; possesses working knowledge of several different practices and of their systematic interconnections; this involves interplay of different strata of mathematical knowledge" (p. 247). However, it does not appear that this argument is conclusive to justify that an agent-based approach of mathematical practice - and of metamathematics in particular - is as relevant an approach as a community-based one. Indeed, individual scientific production relies on professional networks, schools of thoughts, etc., which are meso-level organizations (Whitley, 2000). Thus, mathematical communities have a direct effect on mathematical growth and on individual mathematical practice. From these theoretical considerations, the case study evaluates the role of metamathematics in mathematical change and stabilized mathematical practices in the geometric control theory community.
FROM THEORETICAL CONCEPTUALIZATION TO METHODOLOGICAL IMPLEMENTATION
Operationalizing the notion of collective practices
There are several recent textbooks on geometric control theory (Jurdjevic, 1997; Agrachev & Sachkov, 2004; Bullo & Lewis, 2005), including an internal history (Brockett, 2014; Lewis, 2018). While they provide qualitative information on the mathematical practices shared by geometric control theorists, they do not give material foundation to the underlying mathematical community. Then, to make this notion operational, we will now turn to the study of citational practices. Indeed, citation is an institutionalized practice in scientific research: citing is a performative action which labels the cited papers depending on the function the citing author attribute to them (Moravcsik & Murugesan, 1975). The reasons for citing can be very varied: persuasiveness, positive or negative credit, information, reader alert, etc. (Brooks, 1986). By drawing a line between the cited author and the citing author, a citation enables the latter to claim some (or reject any) cognitive proximity with specific members of a scientific community.
Citing “correctly” is an expected and peer-reviewed literary exercise: when reviewing the state of the art in each field, one has the right to expect certain recognized sources; moreover, citing a reference is a matter of not being blindly critical, nor overly laudatory. The citational practices of a given field constitute implicit norms that young scholars must internalize and failure to comply with them is considered a serious violation of the professional ethics associated with that field (Lemieux, 2012). Since citational practices are collectively regularized, they give indirect insights about some aspects of the practices associated with scientific communities. Indeed, the cited references in a scientific production form a trace of the professional activity, through which certain socio-cognitive relationships between the cited author and the citing author are expressed and endorsed (Milard, 2014). These considerations show that citational practices may be used as a proxy for membership to a mathematical community.
In the first part of the case study, the subjective historical narratives made about the emergence of geometric control theory will be corroborated with a co-citation analysis. We say that author A and author B are co-cited in a given paper if they both appear in the bibliography. Co-citation is a relationship established by the citing author. The more two authors are co-cited by a large number of researchers, the more they can be considered ‘close’ from a scientific perspective. Measuring this closeness is equivalent to measuring the association between authors as perceived by the population of citing authors (Small, 1973). From a set of authors and their co-citations, one can draw a weighted graph whose nodes represent the (most) cited authors and whose edges symbolize occurrences of co-citations. This graph establishes a symbolic map of the existing socio-cognitive connections within the field, whose evolution through time can be observed. Co-citation analysis then provides a tool for monitoring the development of scientific specialties.
The visual layout of the graph represents a simulation of a physical model, in which nodes are electric charges and edges are springs (Eades, 1984). Depending on the choice of the physical parameters, authors who are often co-cited together can appear closer than authors which are less co-cited (the attractive force of the springs compete with the repulsive force between the nodes). Community detection algorithms identify a partition of the graph (into sub-graphs, or communities) which maximizes the internal connectedness over the interconnectedness. A recognized method to perform this task consists in maximizing a quality function called the modularity (Newman & Girvan, 2004), which has been shown to be equivalent to minimizing the energy associated to a spin-glass model (Reichardt & Bornholdt, 2006). Due to their higher degree of connectedness compared to the mean connectedness of the graph, such communities gather authors who are more often co-cited among them, and then can be considered as proxies for scientific communities (Wallace et al., 2009; Gingras, 2010).
The second part of the case study addresses the citational practices themselves to assess how membership to the community of control theory shapes mathematical practices. The discussion focuses on the articles published in 1973 and 1974 by control theorist Sussmann and differential geometer Stefan, because they proved independently and simultaneously quasi-identical results with similar methods. This is a unique opportunity to study whether and how the production and the reception of mathematical results depend on the community. To evaluate this hypothesis, the limitations of scientometrics are compensated with a specific methodology: a thematic labelling of the corpus of the papers citing their contributions is made, and a test of independence is performed on the contingency tables obtained from this labelling procedure. Such a qualitative treatment of the corpus of scientific articles completes the scientometric analysis of the first part and illustrates the fruitfulness of using complementary sociological traditions.
Throughout the entire case study, the role of metamathematics and its articulation with the notion of mathematical community are addressed through textual sources written by geometric control theorists. This textual content is an important material of the case study as it is mobilized to support the hypotheses formulated from the quantitative and qualitative analyses. The dialogue between the textual resources - both mathematical and historical - and the bibliometric analyses allows to operationalize the relationship between metamathematics and mathematical communities. In the end, the sociological content of the case study will support and enable philosophical inquiry, rather than replace it: the former will inform the latter, whose centrality will be preserved.
Empirical and methodological aspects
The corpuses of mathematical articles involved in both parts of the case study have been extracted from the Web of Science bibliographic database, which includes information of authors, journals, and citations. This database is widely used in scientometrics and represents the most up-to-date database on scientific journals (Li et al., 2018). The corpus selected for the co-citation analysis consists of all the articles published between 1968 and 1982 by the SIAM Journal on Control and Optimization4. Although the IEEE Control Systems Society - an organizational unit of the Institute of Electrical and Electronics Engineers dedicated to the advancement of the theory and practice of systems and control in engineering - publishes several journals on the topic of control, they were not selected in the corpus because the current study focuses on mathematical communities. The period 1968-1982 is divided in three sub-periods of five years: 1968-1972 (232 articles), 1973-1977 (328 articles) and 1978-1982 (290 articles). Given that the interest is in the dynamics of the research network in control theory, it seemed appropriate to base the co-citation analysis on this periodization.5
The data extracted from the Web of Science was then parsed on the open-access data analysis platform CorText Manager. Network mapping6 has been performed on the 150 most cited authors7, letting CorText find the optimal threshold for edge filtering8. These choices favor the most endogenous cited authors over exogenous ones. Running the network mapping algorithm with different periodizations (from 1 to 4 periods, determined by CorText), numbers of nodes (150 or 300) and values of threshold (from 2 to 5, the optimal threshold found by CorText on the periods 1973-1977 and 1978-1982), shows that the latter variable seems to be most influential in the partitioning of the graph found by the community detection algorithms9. Overall, the higher the threshold, the more the names attached to geometric control in the literature form an independent community. It is noteworthy that the data associated to the years 1973-1977 appear to be the most robust with respect to changes in periodization, number of nodes and threshold. Visual processing of the graphs and running of the community detection algorithms have been performed on the open-source software Gephi (Cherven, 2013).
The second component of the case investigates some aspects of the citational practices within the community of control theory10 since the middle of the 1990s. It analyzes how the results of Sussmann (1973a, 1973b) and of Stefan (1974a, 1974b) - and in a lesser extent a theorem of Nagano (1966) - have been mobilized in this community. Since there is an interest in stabilized citational practices within or outside the control theory community, the corpus has been restricted to the period from 1993 until March 202011. This time span still contains the majority of papers citing Stefan and Sussmann’s articles, since overall, the number of citing papers published after 1993 is three times the number of citing papers published before 199312. Following standard practice in qualitative sociology (Paillé & Mucchielli, 2012), several labels were then attributed to each paper, depending on how Stefan’s, Sussmann’s or Nagano’s contributions were cited in the papers. The attribution of such labels was made based on the context in which the reference was found, i.e., the text surrounding the reference. It is often obvious that the context refers to one of the chosen labels, while sometimes it may be too vague to firmly choose a category. Hopefully, these cases are rare and barely impact the relative weights of the categories which are of interest for us: being cited for the ‘orbit theorem’ or for the generalization of Frobenius integrability theorem.
The community to which the citing paper belongs was then coded. To carry out this last task, the category to which the journal publishing the paper is associated in the Web of Science database was checked: journals classified in the category ‘Automation’ were considered part of the control theory. Then, there are papers published in journals of other categories, but which can still be considered as belonging to control theory: thus, it was checked whether each of the other citing papers contained ‘control’ or ‘systems’ in the title, in the name of the journal or in the keywords and, in any of the cases, it was evaluated whether the paper could indeed be considered as belonging to this domain. Subsequently, the independence of the variables ‘reason for citing’ and ‘citing community’ was tested in the contingency tables thus obtained. Pearson’s χ2 tests were performed on the tables that met Cochran’s criteria, while a Barnard’s test was performed on the only table that did not meet this criterion (Table 3).
THE EMERGENCE OF GEOMETRIC CONTROL THEORY
“Control theory is the theory of prescribing motion for dynamical systems rather than describing their observed behavior” (Bloch, 2015, p. VI). This field, which lies at the junction of mathematics and engineering, emerged in the 19th century industrial revolutions and blossomed in the first half of the 20th century following the development of aeronautics and the need for the understanding of automation and servomechanisms (Bennett, 1996). After the Second World War, the knowledge of the so-called ‘control systems’ - dynamical systems with feedback loop - became increasingly necessary in fields such as aerospace engineering, cybernetics and early robotics. It was only at the end of the 1950s that conscious steps to formalize control theory as a precise mathematical discipline were undertaken. An important milestone in representing control systems occurred at the beginning of the 1960s, when Rudolph Kalman proposed to consider the feedback input as a control parameter living in an abstract ‘control space’ (Kalman, 1960a). Relying on Kalman’s discovery of the necessary and sufficient condition for a linear control system to be controllable (Kalman, 1960b), the 1960’s were devoted to understanding the behavior of linear control systems, focusing on stability, feedback and hysteresis (Brockett, 2014).
The need for a mathematical description of nonlinear control systems was triggered by the earlier attempts of geometrizing mechanics, and most notably the acclaimed book Foundations of Mechanics by Abraham and Marsden (1967). This stimulated interest in the control theory community toward using geometric and Lie algebraic techniques. In fact, a successful and fruitful attempt to connect the study of differential equations and differential geometry had been already made in 1963 in a seminal paper by Hermann (1963). However, this article did not attract much attention before the end of the decade, when the contributions of control theorists Lobry (1970), Haynes and Hermes (1970) acknowledged Hermann’s insights. Geometric control theorist Jurdjevic (1997) argues that the theoretical orientations of control theory at the beginning of the 1960s - towards automata, logic, and abstract dynamical systems - “led away from geometric interpretations of linear theory and was partly responsible for the indifference with which R. Hermann’s pioneering work of 1963 ENT#091;...ENT#093; was received by the mathematical community” (p. 2). In addition to the explanations proposed by Jurdjevic, geometric control theorist Brockett (2014) also considers responsible the fact that linear algebra and geometry were not widely taught in engineering curricula at that time, and that the learning curve to master these techniques at a sufficient level was steep and compounded by the scarce and uneven literature (p. 2204).
The state of a dynamical system is symbolized by a point in a so-called ‘state space’ and the differential equations governing the system give the trajectory of this point in this state-space, depending on the choice of control parametrizing the system. One of the goals of control theory is to determine, given an initial state x 0 in a n-dimensional state-space - or more generally a manifold M - what is the set Σ ⊂M of solutions in positive time of the system of differential equations parametrized by the control; this set corresponds to the set of states that are reachable from the initial state. A system is controllable from x 0 when the set of reachable states from x 0 is the entire state space, i.e., when Σ = M (Sontag, 1991).
The relationship between control theory and differential geometry relies on the notion of vector fields. It was well-known in the dynamical system community that the set of solutions of a first order nonlinear differential equation on a manifold M could be equivalently seen as an integral curve on the same manifold. Indeed, the differential equation uniquely defines a vector field on the manifold, through the following one-to-one correspondence:
dx/dt = f (x(t), t) ←→ f is a vector field on M
This correspondence can be straightforwardly generalized to parametrized systems of differential equations, i.e. control systems: a given set of differential equations dx/dt = f(x(t), t, u(t)) parametrized by a control u: R → R m then corresponds to a family of vector fields F= (f u ) u on M.
The innovation of Hermann’s (1963) work to solve control theoretic problems relies on drawing a relationship between two important results dating back from several decades: Frobenius integrability theorem and Chow-Rashevskii theorem. Using the above bijective correspondence, Hermann has shown that under adequate conditions, the set Σ of reachable states from x 0 corresponds to the leaf through x 0 of the foliation induced by the family of vector fields F. He provides several sufficient conditions on F, which make the distribution of vector fields induced by F integrable into a (singular) foliation. For at least one of these conditions - when the family is involutive and locally finitely generated - he had proven that the induced distribution was integrable (Hermann, 1962). Today, Hermann’s result is recognized as an important contribution toward the generalization of Frobenius theorem to singular (smooth) distributions and singular foliations, which was eventually proven by Sussmann (1973b) and Stefan (1974b).
Historical accounts of the 1960s-1980s made by control theorists converge in saying that the introduction of geometry in control theory precipitated a change in perspective, which some geometric control theorists qualify as ‘revolutionary’ (Brockett, 2014, p. 2204). This led to the emergence of the field of geometric control theory (Jurdjevic, 1997, p. 2), which then has “steadily ENT#091;grownENT#093; into a well-developed research area” (Lewis, 2018, p. 136). The co-citation analysis of papers published in the SIAM Journal on Control and Optimization in the period 1968-1982 substantiates the narratives of geometric control theorists. SIAM is the acronym for the Society for Industrial and Applied Mathematics, an organization gathering engineers and mathematicians. Founded in 1951, it is characterized by its size and interdisciplinary scope: it is the world’s largest scientific association devoted to applied mathematics. The Society began publishing its own journals in the mid-1960s. The aforementioned journal began printing in 1963 as the Journal of the Society for Industrial and Applied Mathematics Series A: Control. The name was subsequently changed to SIAM Journal on Control in 1966, and it adopted its current name in 1976. The frequent name changes reflect the speed of the disciplinary reconfigurations during this period in this part of applied mathematics.
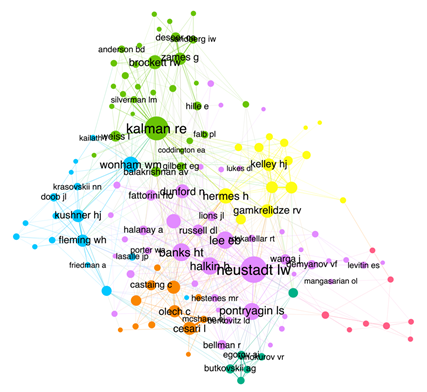
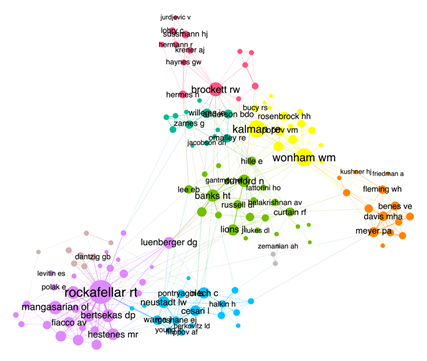
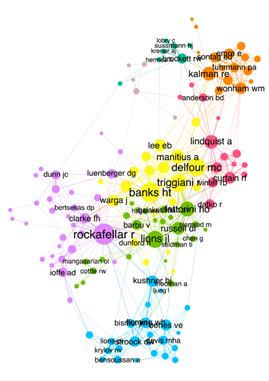
It can be seen that Figure 1 for the period 1968-1972 is very dense. It reflects the state of the field at the end of the 1960s: an effervescence of research topics, without deep specialization. The size of the node associated to Kalman confirms its prominence in the development of control theory as a discipline. Figure 2, covering the period 1973-1977, shows a process of differentiation between several clusters, which seem to direct their research in different directions. More importantly, the presence of the geometric control theory community can be observed (in magenta, at the top). The names appearing in this sub-graph gather the researchers identified in the literature as the founders of this discipline, as well as their main historical references. Their spatial proximity with Kalman’s huge node is a manifestation of their theoretical proximity. Figure 3, covering the period 1978-1982, shows that geometric control theory still forms a distinct community (in dark green, at the top), with a very close relationship with Kalman’s cluster.
Source: Created by the author
Figure 1 150 most cited authors in the SIAM Journal on Control and the SIAM Journal on Control and Optimization between 1968 and 1972
Source: Created by the author
Figure 2 150 most cited authors by the SIAM Journal on Control and the SIAM Journal on Control and Optimization between 1973 and 1977
Source: Created by the author
Note: The size of the nodes varies according to the number of citations of their associated author. The names of the 50 most cited authors are reported (except in Figure 2, where the names Hermann, Jurdjevic, etc., are shown to locate them). The visual layout has been obtained via the Force Atlas algorithm on the Gephi software. The colors indicate the communities determined through the Leiden algorithm: the violet subgraph is the one gathering more nodes than any other, then comes the light green subgraph, then cyan, yellow, orange, magenta, and dark green. The modularity of Figure 1 is 0.51, that of Figure 2 is 0.66 while that of Figure 3 is 0.59.
Figure 3 150 most cited authors by the SIAM Journal on Control and the SIAM Journal on Control and Optimization between 1978-1982
The realization by several control theorists at the end of the 1960s that geometric methods could lead to relevant insights and could solve seemingly intractable problems encouraged them to become acquainted with these tools. Brockett (2014), who was then active, testifies that: “For systems describable by differential equations, this geometric approach seemed to hold the promise of a systematic development of nonlinear control, something that had been completely missing in the past” (p. 2204) The introduction of this new mathematical material led to what might be considered a ‘revolution’ in this sub-part of control theory. This radical change was due not only to the importation of new arguments and constructions, but also to a shift in the metamathematical positions that control theorists had adopted toward their object of research. In particular, the view that merging geometry and control theory was a necessary step in the process of better understanding nonlinear control systems has been widely held in the geometric control community13. This metamathematical opinion has even been formalized by Sussmann (1985), a prominent figure in geometric control theory, who justified the importation of geometric tools as follows:
In our view, the real criterion for deciding whether or not a mathematical theory A has significant applications to a research area B is whether, using A, questions about B can be answered that make sense before A is brought in, but cannot be answered without A (p. 517).
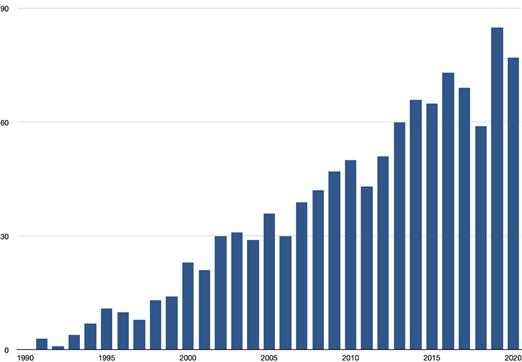
The above citation was written in the mid-1980s, when the community of geometric control theory was still in search for recognition and can therefore be interpreted as an attempt to legitimize the existence of this community. There exist attested cues of the diffuse institutionalization of geometric control theory by the mid-1980s, through textbooks (e.g., Isidori, 1985) and collective volumes (see Fliess & Hazewinkel, 1986). The growing interest in the geometrical aspects of control theory during this decade is illustrated in the preface to the second edition of Isidori’s (1989) textbook: “Synthesis problems of longstanding interest ENT#091;…ENT#093; can be dealt with relative ease, on the basis of mathematical concepts that can be easily acquired by a control scientist” (p. VII). While in the 1980s this community of researchers, bound by this common interest, was sometimes designated under the term ‘nonlinear control theory’14, the name ‘geometric control theory’ enjoyed little recognition before the 1990s (see Figure. 4). As of today, control theorist Lewis (2018) claims that geometric control theory forms a distinct community with a clear and well-established topic of research, synthesized in various texts (p. 136).
A COMMUNITY-CENTERED PERSPECTIVE ON MATHEMATICAL KNOWLEDGE
What is the ‘orbit theorem’?
The emergence of geometric control theory at the beginning of the 1970s paralleled the publication of two simultaneous decisive contributions by control theorist Sussmann (1973b) and differential geometer Stefan (1974b), who independently proved two results. The first one states that the orbits of a family of vector fields on a given manifold are immersed submanifolds. In modern day control theory, this result is designated under the name ‘orbit theorem’ (see Figure 5). Although this mathematical result had been mobilized in geometric control since the publication of Sussmann’s and Stefan’s work in 1973 and 1974, this label was not attributed to it for at least a decade. The denomination ‘orbit theorem’ appeared first as an indefinite generic name at the beginning of the 1980s15. The personification of this label -attributing its origin to several authors - did not occur before the end of the 1980s, as control theorist Sontag (1986) was still using the indefinite denomination in 1986. The orbit theorem is considered a founding element of geometric control theory since it describes the differentiable structure of the sets of reachable points of a control system. To emphasize the centrality of this result in this community, Jurdjevic (1997) goes so far as to state that “the ‘orbit theorem’ marks a point of departure for geometric control theory” (p. 32).

Source: The first theorem is by Jurdjevic (1997, p. 33), the second by Agrachev and Sachkov (2004, p. 63), and the third by Bullo and Lewis (2005, p. 373)
Note: The statement of the orbit theorem can have several forms, although at least all include the first statement and more generally all correspond to Theorem 4.1. of Figure 6.
Figure 5 Excerpts from several textbooks on geometric control theory

Source: Excerpt from Sussmann’s (1973b, p. 179) original paper
Figure 6 Distinction between 1) the so-called "orbit theorem" (Theorem 4.1.) and 2) the generalization of Frobenius’ theorem (Theorem 4.2.)
The second result proven by Stefan and Sussmann in their 1973-1974 articles (Sussmann, 1973b; Stefan, 1974b) is a generalization of Frobenius integrability theorem. This theorem was formulated by the mathematician Frobenius in 1877 as a decisive contribution in the solution to the ‘problem of Pfaff’ (Hawkins, 2013). This result, in a modern formulation, states that a smooth regular distribution is integrable into a regular foliation if and only if it is involutive16. When the distribution is no longer regular, i.e., when its rank is not constant and possesses singularities, the involutivity condition is no longer sufficient. In 1962, Hermann extended Frobenius’ result to locally finitely generated smooth singular distributions; in 1966, Tadashi Nagano generalized it to analytical singular distributions; and in 1973, Stefan and Sussmann independently showed that it could be extended to smooth singular distributions.17
A preliminary study of the mathematical literature citing the results of Stefan, Sussmann and Nagano, led to the hypothesis that citational usages were dependent on the citing community. In control theory, these authors seem to be cited mainly for the orbit theorem, while outside control theory, they were cited mainly for the generalization of Frobenius integrability theorem18. These differences are visible both at the level of citational practice and at the level of mathematical knowledge production. In fact, the papers of Sussmann and Stefan differ in their respective emphasis: on the manifold structure of the orbits, on the one hand, (Sussmann), versus the characterization of foliations with singularities by means of foliated atlases, on the other (Stefan). Although the mathematical objects that are central to their proofs differ only slightly19, the differences between their respective mathematical motivations are reflected in the way they prove their results: the former uses a tedious topologically-oriented proof, while the latter uses a more geometry-oriented one.
Hector Sussmann was born in Buenos Aires in 1946. After earning a degree in mathematics in 1966, he went to the Courant Institute (NYU) to complete his doctorate in applied mathematics, which he defended in 1969. In his paper published in the Transactions of the AMS, Sussmann (1973b) is primarily motivated by control theoretic considerations: finding the differentiable structure of the orbits of a family of vector fields, because under some conditions they correspond to the reachable sets of a control system. This explains the order in which he addresses the problem (see Figure 6): in his paper, he first distinguishes the results demonstrating the differentiable structure of the orbits and then presents the generalization of Frobenius theorem as a mere consequence of the first more fundamental results. This hierarchical presentation is made explicit in the introduction of his article and was even transparent in the short letter he published a few months earlier in the Bulletin of the AMS to advertise his result (Sussmann, 1973a). The journals in which Sussmann published his letter and his main paper belong to the American Mathematical Society and are intended for a large audience. This would explain why Sussmann uses in his paper a general-purpose mathematical language that does not include the linguistic and notational specificities of control theory (which can be found in some of his papers of the same period).
Simultaneously, Peter Stefan, then a Slovak refugee and a PhD student in differential geometry at the University of Warwick, proved the same results (Stefan, 1974b). While the methods were similar, his goals were distinct. His work focuses on singular foliations, even if he seems sufficiently acquainted with control theory to employ its vocabulary: he received an education in this field and contributed to it before leaving Prague (Brown & Eells, 1981), and he certainly attended the first international conference on geometric methods in control theory as his contribution appears in the proceedings (Stefan, 1973). The first page of the first section of his 1974 paper published in the Proceedings of the London Mathematical Society is devoted to defining singular foliations and their leaves. This is very important because Stefan is the first to provide an explicit definition of singular foliations in terms of local coordinates, thus mimicking the well-known definition of regular foliations through foliated atlases and charts. Both in his paper and in the letter sent to the Bulletin of the AMS in March 1974 to advertise his result (Stefan, 1974a), Stefan puts the emphasis on the foliation structure equipping every partition of M into orbits. Stefan considers the differentiable structure of the orbits to be an intermediate result: it is mentioned as a side remark in Theorem 1. (see Figure 7), and appears in his proof as a consequence of Lemma 3.1. The generalization of the Frobenius theorem corresponds to Theorem 5. of his paper, which is a reformulation of Theorem 1. in the context where the arrows are vector fields. During the years following the publication of his original paper, Stefan focused on deepening his understanding of the integrability conditions of singular smooth distributions into singular foliations. His last article - edited and published after his accidental death during a hike on Mount Tryfan in Wales in 1978 - is a summary of what was known at that time about the integrability of families of vector fields (Stefan, 1980). This supports the idea that he was primarily interested in the study of singular foliations.

Source: Excerpt from Stefan’s (1974b, p. 701) original paper
Note: Theorem 1. is the main theorem presented in the beginning of the article from which Stefan generalizes Frobenius theorem. He emphasizes that the partition of M by the "accessible sets" (which he chose over the term ‘orbits’) forms a singular foliation.
Figure 7 Theorem 1
What do you cite for? Where do you cite from?
While Stefan’s and Sussmann’s contributions were produced for different objectives, they have also been received very differently within and outside the control theory community. In the citing corpus over the period 1993-2020, four main situations can be identified: 1) when the citing article refers to their papers for having proven the orbit theorem; 2) when the citing article refers to their papers for having proven the generalization of Frobenius integrability theorem; 3) for definitional purposes, such as for the definition of orbits or singular foliations; 4) as mere routine reference. The number of times Stefan or Sussmann were cited alone was also calculated. The proportion of each one of those categories is presented in Table 1.
Table 1 Most common reasons for citing in articles indexed in the Web of Science database and citing Štefan (1974a, 1974b) and Sussmann (1973a, 1973b) between 1993 and March 2020

Note: The table should be read as follows: “From 1993 to March 2020, 47 % all papers citing one or both Stefan's (1974a, 1974b) articles do it for his generalization of Frobenius theorem”. Notice that the sum of the percentages of the first four columns may go beyond 100 % because some articles in the corpus refer to Stefan or Sussmann for several different reasons.
Source: Created by the author.
Although Stefan and Sussmann simultaneously and independently proved similar results, there is no consensus on what their main contribution is, be it understood as the orbit theorem or as the generalization of Frobenius theorem. However, some variations in Table 1 may be explained by the different aspects favored by one author over the other. For example, the fact that Stefan is much more cited for definitional purposes certainly comes from the fact that the definition of singular foliations plays a prominent role in his paper. The authors are co-cited 108 times, which implies that 92 % of the time Stefan is co-cited with Sussmann. Usually, when they are cited in the same paper, they are cited for the same reason, in the same place of the text. The last column shows that Stefan is almost never cited alone (in only 8 % of the papers citing him), whereas Sussmann is cited alone two-third of the times. This might be explained by the fact that the references to Sussmann come mainly from the field of control theory, in which he is an important figure, while Stefan’s early death may have influenced his near disappearance from the citational landscape. To refine the analysis, the community to which each cited paper could belong was evaluated on the basis of bibliographical data (see Table 2 and 3).
Table 2 Number of citations of Sussmann’s (1973a, 1973b) contributions, with respect to the given reason and the origin of citation

Source: Created by the author.
Table 3 Number of citations of Stefan’s (1974a, 1974b) contributions, with respect to the given reason and the origin of citation
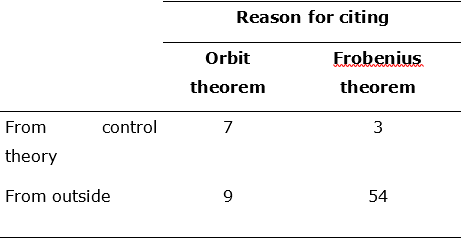
Note: The tables should be read as follows: “Outside of control theory, Sussmann has been cited forty-six times for the orbit theorem, while in control theory he has been cited thirteen times for the generalization of Frobenius theorem”.
Source: Created by the author.
Stefan is disproportionately cited for the generalization of Frobenius integrability theorem outside control theory (Table 3). Sussmann is also widely cited for this reason, but he is also cited almost as much for the orbit theorem (Table 2). Notice that while in control theory he is cited twice as much for the latter than for the former, the situation is reversed outside control theory. These contingency tables support the preliminary observation20 that outside control theory the contributions of Stefan and Sussmann are associated with the generalization of Frobenius integrability theorem, while within control theory they are associated with the orbit theorem (hence without much emphasis on the foliated structure of the ambient manifold). This result confirms also the claims made by geometric control theorists that the orbit theorem is quite central to their mathematical practice.
It might be objected that the differences in citational practices may be artificial because there are two distinct results in Stefan’s and Sussmann’s contributions (see Figure 6 and 7). This is not surprising because when they wrote their respective articles, both Stefan and Sussmann had different objectives and emphasized different aspects of their work. However, this justification is not convincing: indeed, it cannot explain the fact that mathematician Nagano (1966) is also cited for the orbit theorem in control theory. Nagano is a Japanese mathematician who proved in 1966 a generalization of Frobenius theorem in the analytic setting. The presentation of the result in his paper shows a clear intention to affiliate himself with Frobenius, and Velimir Jurdjevic testifies that Nagano was totally disconnected from the community of control theory (Jurdjevic, 1997, p. 63). This is confirmed by the study of the literature, since the first recorded mention of Nagano in control theory21 was made in a relatively unnoticed paper of 1971 (Elliott, 1971), and then in Sussmann’s (1973a) letter as a mere reference since his proof does not rely on Nagano’s ideas. Moreover, control theorists Lobry (1970), Haynes and Hermes (1970) had already started mentioning Hermann’s fruitful geometric approach in the late 1960s, without mentioning Nagano’s work either.
However, today his name is referred to in control theory as an important milestone in the conceptual foundation of the body of knowledge associated with geometric control, and he is sometimes presented as a precursor of the orbit theorem (along with Hermann). For example, in contemporary geometric control theory textbooks, the orbit theorem is alternatively attributed to Hermann and Nagano (Jurdjevic, 1997, p. 48), or to Nagano and Sussmann (Agrachev & Sachkov, 2004, p. 63), or to Stefan and Sussmann for the smooth case, and various authors (among whom belongs Nagano) for the analytic case (Bullo & Lewis, 2005, p. 110). A bibliometric analysis of the contemporary literature citing the 1966 paper of Nagano shows that the reasons for which he is cited in control theory do not correspond to his original intentions: providing a generalization of the Frobenius theorem to the analytic setting (see Table 4). Indeed, in the citing corpus over the period 1993-2020, three main thematic categories can be identified22: 1) for the generalization of Frobenius integrability theorem to analytic singular distributions; 2) for the orbit theorem; 3) for the accessibility rank condition - or Hörmander condition. The last label designates in control theory the condition that a vector field family must satisfy for its orbits to coincide with the entire state space (in that case, there is only one orbit). It is often reformulated as a characterization of the tangent spaces of the orbit; then, in this form, this condition is usually part of the orbit theorem (see for example item (2) of Theorem 5.1 and item (ii) of Theorem 7.5 in Figure 5).
Table 4 Number of citations of Nagano’s (1966) paper, with respect to the given reason and the origin of citation
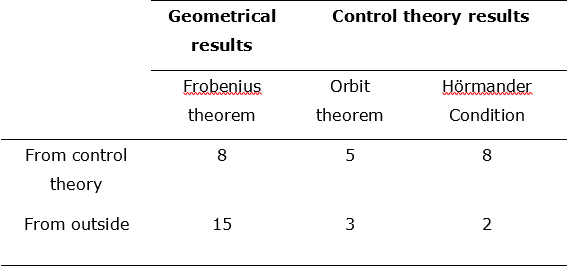
Source: Created by the author.
Outside control theory, Nagano has been overwhelmingly cited for his generalization of Frobenius integrability theorem. In contrast, in control theory, he has been as evenly cited for this result as for the Hörmander condition, and in a lesser extent for the orbit theorem. This correlation suggests that the reason for citing is highly dependent on the origin of the citation23. This not only supports what has been seen for Stefan and Sussmann - that the community of control theory shares particular citational practices that differ from those outside of control theory - but also proves that, in the particular case of Nagano, control theorists attribute endogenous labels to a mathematical result that was not originally related to their field, nor was it intended to be promoted to the status of a theorem. Indeed, in his 1966 paper, the fact that the leaves of an analytic foliation are immersed submanifolds - the infamous ‘orbit theorem’ that control theorists refer to - is an intermediary step in the proof of Nagano's theorem.24
CONCLUSION
What then is a theorem?
Several actors agree on the sharp turn that the study of nonlinear control systems took in the 1970s, when the geometric perspective was introduced and became a defining element of this mathematical community (Jurdjevic, 1997; Brockett, 2014; Lewis, 2018). The centrality of the geometric approach to study systems of differential equations is still recognized in the 2000s, as illustrated by Bullo and Lewis (2005) in the preface of their textbook: “… at some point the unity offered by a differential geometric treatment becomes advantageous and we feel that this is merely a necessary part of the subject, as we see it” (p. X). Geometric control theorists not only defend the (metamathematical) view that geometric approach is fruitful - and even necessary - to solve their problems, but they also claim that it contributes to produce a new mathematical significance on their object of research.
Indeed, control theorist Brockett (2014) argues that although the introduction of geometric techniques created a schism with engineers, it opened up points of contact with physics and mathematics (p. 2204). In particular, geometric control theory is tightly related to other subfields of mathematics such as Cauchy-Riemann geometry, hypoelliptic differential equations or sub-Riemannian geometry, etc.25 Thus, some geometric control theorists (such as Agrachev) publishes articles in pure mathematics journals, as well as in dedicated control theory journals. The existence of such interconnections between sub-communities, echoes Ferreirós’ and Zarca’s belief that the interconnectedness of mathematics is a fundamental property of this discipline. These successive arguments show that geometric control theory appears as a smaller community inside the broader community of control theory, with its own metamathematics and independent ties to other mathematical communities that other specialized communities within control theory do not share.
The second part of the case study has then shown that these specific collective metamathematical views impact the production and the reception of mathematical contributions in control theory. The intention of Stefan to affiliate himself with the Frobenius theorem was explicit, whereas Sussmann chose to emphasize that the orbits of a control system form immersed submanifolds of the state space. This mathematical result, later recognized as a founding element of geometric control theory, has been subsequently labelled under the denomination ‘orbit theorem’. As the case study shows, this theorem - associated by control theorists to Stefan, Sussmann, Hermann and Nagano - seems not to be much mobilized outside of control theory. This situation can be explained by the fact that the results of Stefan and Sussmann sit at the border between control theory and differential geometry. The two communities then refer differently to these results because they are not interested in the same problems. A certain mathematical community may consider that the key point of a theorem lies not in the original intention of the author, but in the applications this community finds in it. Therefore, the original statement of a theorem may differ from the way it is invoked years later in each mathematical community, because some aspects of mathematical knowledge have stood out and shape what is considered as interesting or not.
A similar question had already been investigated in the 1960s by sociologist Fisher (1966). He studied the perceived status of the (dying) theory of invariants in the mid 20th century and observed that “different groups of mathematicians evaluate the theory differently within their mathematical Weltanschauung26 ENT#091;and thatENT#093; these classifications and evaluations evolve over time” (Fisher, 1966, p. 138). This emphasizes the local properties of metamathematical opinions: they are not homogeneously defined across all communities, but rather localized and dependent on the community, precisely because they form the basis of collective practices. In the same way, in the case study of the present article, control theorists single out the ‘orbit theorem’ from the contributions of Stefan, Sussmann and Nagano, because it provides the crucial assumptions from which every mathematical reasoning in geometric control theory can be made. Thus, it seems that the label ‘orbit theorem’ plays a particular role in this community.
Attributing a name to a mathematical statement is a performative and socially regularized act. It aims at pointing to a set of cognitive contents that go beyond the limits established by the original statement: “Theorems are in a sense just tags, labels for proofs, summaries of information, headlines of news, editorial devices” (Rav, 1999, p. 20). The denomination ‘orbit theorem’ thus conveys not only a cognitive meaning (the statement, per se), but also a metamathematical meaning: that of being an institutionalized manifestation of geometric control in mathematical knowledge. Applying a label allows different generations of mathematicians to refer to an object that is neither completely the same, nor completely different, but which remains a powerful marker of social membership to the community that uses this label.
Therefore, the orbit theorem is much more than a mathematical statement: it carries collective metamathematical representations. Grasping this content could not have been possible without mobilizing the notion of mathematical communities. The case study demonstrates that mathematical knowledge is primarily a collective knowledge, and that mathematical practice is a collective practice. It is interwoven with socio-historical aspects in a way that could not be reduced to the oversimplified picture of the interaction between an agent - the mathematician - and an external socio-historical background. Rather, the interplay of the collective practices with which a mathematician has been acquainted in her professional life crystallizes in her unique individual practice. Thus, a philosophical inquiry about individual mathematical practices cannot be complete without acknowledging the role of mathematical communities and of their associated practices. Their importance is even more crucial in contemporary mathematics, which have been characterized by their increasing professionalization and internationalization since the Second World War.
A central aspect of mathematical practice consists of the metamathematical component, for it shapes not only the way mathematicians conduct their work, but also how they interact with exogenous mathematical knowledge. Then, grounding the philosophical notion of metamathematics in the sociological notion of mathematical community is a decisive movement to make the concept of collective practice operational. This makes it possible to highlight community-dependent aspects of mathematical production, which in turn demonstrates that institutionalized and settled mathematical knowledge is not unified but is susceptible to variations across communities. In time, it could be very informative to deepen these sociological considerations and to study the differentiated usages to which mathematical objects are subject in different communities. Thus, reinstating the collective dimension of mathematical work brings a much more dynamical perspective to the study of mathematical practices and their interplay. This illustrates how the use of sociology of science benefits the philosophy of mathematical practice.