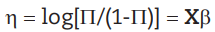Coaligarse o no coaligarse y el emprendimiento

Establecer una colaboración para el desarrollo de nuevos equipos o tecnologías es muy común. Esto aparece referido como tareas de R&D o de joint venture en la literatura anglosajona. Consideremos una población de firmas que participan del mercado de un bien. Cada una tiene un fondo para investigación acotado y da señales al mercado tales como fidelidad a la marca, nicho de mercado, calidad percibida por los clientes, nivel de sus dispositivos de investigación y desarrollo (ID), etc. Este es un tema que es tratado en diversos trabajos como los de ^{Veugelers (1998)}, ^{Yi (1998)}, ^{Ray y Vohra (1999)}, ^{Shane et al. (2016)}, ^{Anderson (2015)}. Los productos de cada firma están diferenciados ligeramente. Las firmas por su parte compiten en el mercado pero evalúan cooperar para el desarrollo de nuevas tecnologías. Por ejemplo, ^{Aloysius (2002)} señala los casos de IBM y Lucent Technologies, quienes comparten el mercado de circuitos integrados para aplicaciones específicas a través de unidades vendedoras. Similarmente, ocurre con Intel y Advanced Micro Devices en el mercado de microprocesadores, Hyundai, Motorola y Phillips, en tecnología para telefonía celular, o usuarios finales de tecnologías de punta en sus productos acabados como Compaq y Hewlett-Packard.

En estos casos, las firmas envían como señales sobre sus potencialidades para desarrollar parte de una nueva tecnología a otras firmas. Las firmas evalúan estas señales para establecer si la probabilidad de que sea exitoso el coligarse con ella es alta o no y si esto es suficientemente beneficioso, entonces, ¿representará una ventaja para las empresas, en términos de la utilidad, coaligarse?

Este problema lo podemos modelar usando la propuesta de ^{Aloysius (2002)}. Desde el punto de vista de la Teoría de Juegos podemos considerar la existencia de una población de firmas Todo subconjunto S de esta población es una coalición. En términos de la Teoría de Juegos debemos considerar que cada firma tiene un presupuesto acotado y se busca obtener un beneficio por tomar como decisión que la señal da signos de que lo mejor es aceptar la incorporación a la coalición. Si a la firma i le cuesta el entrar en la coalición, lo que depende de la tecnología y la potencialidad investigativa que aporta, entonces la coalición asumirá la tecnología más barata aportada por los miembros de ella. Por tanto el costo del desarrollo de la nueva tecnología es: . Si cada firma obtiene una fracción de beneficio lo que busca al coaligarse puede ser caracterizado por resolver el problema de optimización:

Donde solo si la firma “i” decide entrar en la coalición. Los otros miembros de la coalición envían señales a esta firma y valoran si querrá incorporarse. Para ello necesitan establecer si 1 es suficientemente grande.

Algo similar harán los promotores de una cooperación para desarrollar una nueva tecnología. Analizando las señales enviadas por las firmas sobre su capacidad tecnológica y su éxito, en empeños previos de investigación-desarrollo y/o su desempeño en el mercado, se considera si la firma decidirá integrarse o no a la cooperación. Por su parte, una firma puede analizar la actitud de las demás para enviar señales sobre cuál considera que debe ser su fracción .

La modelación

Un enfoque se basa en el análisis de la utilidad. Consideremos que el agente receptor (AR) recibe señales del mercado y desea estudiar el comportamiento de una función de utilidad

Donde los son parámetros desconocidos, las s son variables de control y es un error aleatorio de esperanza cero y varianza constante. Un ejemplo de tal función de utilidad está dado por la riqueza del agente a partir de la estructura de su portafolio de acciones. En este caso es el número de acciones del bien representa los pasivos del agente receptor (AR) en cuentas bancarias y el resto de los parámetros el valor de un bono del bien correspondiente. En el caso de la cooperación en ID la firma tiene un nicho en el mercado en los productos t = 1,.., p y un pasivo B₀. Considera que el bien t le aporta una ganancia B_tY_t. Relacionemos la señal que obtiene con la variable

Z=1, si la señal sugiere a i que ejecute cambios en su vector de bienes.

Z=0, si la señal sugiere a i que no ejecute ninguna acción.

Cuando Z=0 el AR no considerará cambiar y su riqueza no se ve afectada. Si Z=1 él puede cambiar y tomar un como el vector con los nuevos valores de la variable de decisión, la estructura de las acciones del portafolio. Al cambiar se incrementa el bien t en . Es decir, con la decisión de cambiar su utilidad sería:

El cambio en la utilidad es

Donde . Por su parte representa el cambio en la utilidad del agente debido a cambiar Y_it por X_it ^t haciendo caso a la señal.

Vamos a considerar solo el caso en que los parámetros no varían con la decisión tomada para t = 1,.., p. Entonces la esperanza del cambio es igual a

Note que en el caso de un solo bien el agente va a ser indiferente ante la señal si se fija como solución

En la práctica, el AR considera la existencia de diversos escenarios posibles. Cada uno debe generar una señal que al ser identificada le llevaría a fijar un valor de Z.

Consideremos que el AR analiza el mercado y observa una señal S_h Entonces toma una decisión asociada a un vector del conjunto Su interés es establecer si cierto x_i, que cree está asociado a la señal es adecuado por considerar que el valor de la variable aleatoria es Z=1. Si es alta, entonces, al observar la señal decidirá cambiar su portafolio con estructura

por el dado por x. Esto se asocia a la valoración de si (U_i toma valores positivos suficientemente altos.

Aceptemos que el número de realizaciones observadas en el mercado lleva a que:

n_i= número de observaciones en que es suficientemente grande para aceptar que .

Una mentalidad estocástica lleva a que el AR desee establecer cuál es la función de distribución del incremento de la utilidad, es decir,

Analizando una muestra de tamaño , evaluará las variables Bernoulli

Y_i(h)=1, si se genera una señal que determina que se debe cambiar a

Y_i(h)=0, si se genera una señal que determina que no se debe cambiar

Es decir que Y_i(h)=1 si y solo sí . Aunque estas variables de Bernoulli no sean independientes, dado el tamaño de la muestra,

, se distribuye como una Binomial, .

El problema debe ser resuelto a través de la estimación de ((x). Podemos usar el estimador naive:

Dadas las hipótesis sobre los ni’s: , y considerando que el orden de convergencia soporta la aceptación de que .

Si el experimento es diseñado se observan ni resultados del efecto de enviar la señal xi. Esto, por ejemplo, será de interés para una agencia considerada como el gestor de formar una coalición. Se envían señales y se observa el comportamiento de los receptores. A partir de su estudio ellos deciden qué política llevar para comunicarse exitosamente a través de un sistema de señales.

Como cada señal corresponde a un solo vector y las n respuestas son representables por la matriz

donde hay n_i, réplicas del vector .

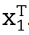Por otra parte la Ley de los Grandes Números garantiza que

Donde ( representa un vector cuyas k componentes son iguales

.

Otra situación es aquella en la que se obtienen n señales y se identifica que ni de ellas corresponden a x_i. Consideremos que estas fueron generadas por una de H clases posibles y que hay m posibles señales. El gestor analiza la firma aspirante y considera si puede ser del tipo C_j, j=1,..., H, tal como ocurriría con un corredor de bolsa, que debe evaluar situaciones del mercado cambista, con la finalidad de tomar la mejor decisión.

Ahora n_i continúa siendo una variable aleatoria y el interés está en la variable Z_ij = j si x corresponde a la señal i y pertenece a C_j (Z_ij = 0 en otro caso).

El AR se interesa en conocer:

Ahora

Tomando en otro caso).

Al igual que en el modelo anterior el interés está en estimar

Una contrapartida del estimador de ((x) propuesto anteriormente es

Consideremos que es válido el conjunto de hipótesis

H1:

Un par de relaciones de interés teórico necesarias son que H2:

H2.1. Existe solo un se cumple que

H2.2 Existe solo un 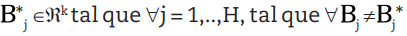se cumple que

Cuando se cumplen H1 y H2.1 tenemos el modelo logit y si fuera H1, H2.2 el multinomial y la convergencia de los estimadores dados en (1) es garantizada.

Otra forma más clásica es usar los modelos logit y log-lineal para hacer la estimación de los parámetros usando el método de máxima verosimilitud para obtener las probabilidades. Este enfoque establece que los agentes involucrados van a utilizar distintos modelos para establecer cómo evaluar la probabilidad de que su utilidad sea incrementada al coaligarse. Utilizando los criterios predominantes en el mercado el AR determina k escenarios. Evaluando ni experiencias similares le interesa conocer

P’_i = proporción de firmas que entrarían en el escenario i.

Usando como función de enlace la canónica

donde,

( vector de predictores lineales.

X = matriz de dimensión kxp.

= vector paramétrico de dimensión p.

El método de máxima verosimilitud (MV) es el más usado para hacer los ajustes, véase Fahrmeier-Tutz (1994). Pueden ser usados como algoritmos el Genmod del sistema SAS 8.10 y el GLM aplicado sobre R. Véanse experiencias recientes sobre su uso en ^{Gentleman (1996)} y ^{Barreto y Kypreos (2004)}. Un análisis del método general puede ser obtenido en ^{Agresti (1990)} y en ^{McCullagh-Nelder (1989)}. Véanse particularidades sobre los algoritmos usados en el paquete SAS en ^{Little y Yau (1996)} y ^{Wolfinger (1999)}.

La desviación:

donde, . Esta es calculada para establecer la bondad del ajuste y, dado que la devianza binomial residual se distribuye (2 (k-p), se probará si el modelo es adecuado usando la prueba chi-cuadrado. Se estima la dispersión utilizando:

El cual estima la escala (. Este es el estimador de momentos del estadístico generalizado de Pearson, ( es el vector de variables dependientes ajustado y (* el estimador de (, véase ^{McCullough-Searle (2001)}. Este estimador permite establecer la existencia o no de superdispersión. Esto es válido cuando es significativamente grande.

El AR espera que si la probabilidad de éxito es suficientemente grande es conveniente unirse en la joint venture. Si el aspirante conoce el modelo usado estará en condiciones de estimar esta probabilidad.

Comparación de los diferentes estimadores mediante un experimento de Monte Carlo

Compararemos los resultados asociados al uso de los estimadores calculados con los algoritmos dados en SAS y R, dado que tienen integradas las funciones para las estimaciones, respecto a la estimación realizada usando los estimadores Naive (1) y (2).

Consideremos que el orden de convergencia soporta la aceptación de que . Véase ^{Hadjicostas (2003)} para una discusión de problemas de este tipo. Para ello consideraremos una firma con p = 10 y k = 5 escenarios. En cada uno se generaran 1.000 vectores x que producen una ganancia dentro de un rango . Tenemos en cuenta señales generadas aleatoriamente que dan información sobre realizaciones de los diferentes escenarios. Se generaron 500 vectores y con ellos se evaluó el modelo para estimar la probabilidad de obtener un valor aceptable de la ganancia. Se consideraron dos métodos de muestreo: se hace un muestreo tomando en cuenta la estratificación por tipo de escenario y, en el segundo, no se tiene en cuenta la estratificación.

Para cada uno de los métodos se indica el porcentaje de veces en que se aceptó el modelo usando D(P’, P*), la estimación de la dispersión y el promedio de la norma. El promedio de la norma se define como ||probabilidad estimada-probabilidad real|| y se denota por . Los resultados se brindan en la tabla 1.

Tabla 1 Exactitud de los métodos 

Fuente: elaboración propia a partir de datos simulados.

Como se ve en la tabla 1, Genmod computa estimadores que son los de menor dispersión y la propuesta Naive (1) es la menos confiable en estos términos. En general, al considerarse la devianza, el comportamiento de los estimadores es aceptable. El modelo es aceptado con una frecuencia muy cercana a la fijada por la teoría excepto para (1). Para (* también GLM-R1.6.1 es el mejor en términos de la aceptación del modelo como correcto. Las otras alternativas no difieren considerablemente. Sin embargo (1) tiene los mejores valores de (. Esto conlleva a que la elección de uno de los estimadores como el mejor globalmente no sea posible sino sobre la base de criterios del decisor.

En el caso en que el número de fracasos sea superior a lo esperado de una distribución binomial un enfoque es considerar que la distribución de los éxitos está contaminada con una distribución degenerada que tiene probabilidad uno de no observar un éxito. Diversos autores han acometido el estudio de esos modelos como es el caso del trabajo de ^{Breswlow y Clayton (1993)} y ^{Deng y Paul (2002)}. En este caso, un modelo adecuado es suponer que el juego en que estamos involucrados ha sido afectado por un cierto shock que genera un número alto de no-éxitos inesperadamente. Tomemos un vector de efectos aleatorios (i para modelar este fenómeno. Sea , con probabilidad con probabilidad 1-Q_it) una variable aleatoria. Ahora , siendo el vector de las como el de las probabilidades de mezcla Bit las que son funciones de las covariables.

mide la sobredispersión en la prueba desarrollada por ^{Berenhaut (2002)}, dando origen al modelo es el vector de los el vector de parámetros de la regresión,

B = ( B₁ ^T ,..., B_k ^T )^T y W = ( W1T ,..., WkT )T matrices de diseño. Para las probabilidades de mezcla el modelo es Logit(Q_i ) = , donde es el vector de parámetros de la regresión y G = ( G1T ,..., GkT )T

y W = ( W₁ ^T ,..., W_k ^T ) matrices de diseño. El cómputo de los estimadores se llevará a cabo usando el software SAS’ PROC NLMIXED.

La existencia de shocks va a modelarse introduciéndolas por variables aleatorias, uniforme en (0, 1), Qij. Aplicamos los métodos de cómputo de estimadores utilizados en el experimento reportado en la tabla 1. Comparamos sus resultados con los obtenidos con este último cuando el modelo efectivo es el asociado al shock. Es decir, la firma desconoce el cambio en el mercado y utiliza los datos observados utilizando un estimador que realmente no es máximo verosímil.

La tabla 2 brinda los resultados obtenidos al analizar las muestras generadas. Las distribuciones incluidas en el estudio tenían el mismo parámetro de escala. Las observaciones en la base de datos fueron transformadas al generar el correspondiente usando la distribución prefijada. Las distribuciones utilizadas en la experimentación fueron: la uniforme en , la normal, la Cauchy y la doble exponencial (Laplace) con esperanza 0 y escala _it y la exponencial con media .

Los resultados en la tabla 2 establecen la superioridad en términos de exactitud del uso de los estimadores Naive siendo el (2) ligeramente superior que el (1) en la mayoría de las experiencias. Genmod-SAS tiene un buen comportamiento para las llamadas “distribuciones alfa-estables”: Cauchy y normal. Estos resultados califican los estimadores Naive como una opción aparentemente robusta.

Tabla 2 Exactitud de los estimadores medida por bajo diversas distribuciones de con parámetro de escala  

Fuente: elaboración propia a partir de datos simulados.

Otro enfoque de este problema sería considerar que, en vez de un shock hay un componente aleatorio que afecta la evaluación que se hace de las señales enviadas por las firmas que pueden integrarse a la coalición. Tengamos en cuenta que debe considerarse en el modelo de la respuesta la existencia de este factor utilizando el vector aleatorio ui y establecer que su efecto es medido por el factor . Note que este se distribuye condicionalmente de acuerdo con una binomial con esperanza . Denotaremos Y* = y por r al vector cuya componente i-ésima es ri = Y*i /mi. Tomando , la matriz de efectos fijos como Xkxp y la matriz de efectos aleatorios Dkxq el modelo a usar es

Para resolver el problema de la estimación véase ^{McCullough-Searle (2001)}, el uso de la quasi-log verosimilitud penalizada conjunta

Se considera en su construcción que u sigue una distribución normal q-variada N(0,G).

El problema de optimización asociado es complicado pues, la variable dependiente ajustada, debe ser aproximada por:

Lo que garantiza que: .

Usando el macro GLIMMIX y el procedimiento PRC MIXED del SAS 8.10 los estimadores son evaluables. Otra alternativa es ajustarlos usando el comando glmmPQL, que es básicamente un procedimiento de mínimos cuadrados reponderados iterativamente, del ambiente R 1.6.1 basado en el método de Newton-Raphson para ajustar el modelo generalizado, mientras que usa el EM para resolver el problema de optimización planteado en la estimación de los componentes de la dispersión asociados a los efectos de u. Una discusión sobre cómo trabajan los algoritmos de maximización conjunta que aparecen en ambos procedimientos es brindada por ^{Breslow-Clayton (1993)}. El ajuste del modelo es evaluado por el test de superdispersión basados en el estimador de la componente de extradispersión: es el estimador del vector de estimadores el rango de X y u la predicción de u. La prueba se basa en comprobar si este estadístico de prueba soporta que el parámetro es significativamente mayor que 1. Vea ^{Schall (1991)} para una discusión sobre este y el algoritmo usado para su determinación.

Utilizamos las mismas características del experimento de Monte Carlo efectuado para el caso de los shocks, con el fin de generar los efectos aleatorios. En este caso usado como desviación típica a .

Tabla 3 Exactitud de los estimadores medida por bajo diversas distribuciones de ui con parámetro de escala  

Fuente: elaboración propia con datos simulados.

Los resultados del algoritmo programado en el ambiente R 1.6.1 son mejores que los brindados por el del SAS en términos de pues están más cerca de cero en todos los casos. Ambos algoritmos establecen siempre la aceptación de la consistencia de la varianza con la distribución asumida, lo que evidencia la no-existencia de superdispersión. Sin embargo, GLIMIX PRC MIXED SAS 8.10 tiene valores menores de V2 en todos los casos.