Introducción
En la actualidad, la enseñanza de las matemáticas está mediada por el uso de tecnologías digitales que pretenden, desde su uso más básico, facilitar los procesos de aprendizaje entre los estudiantes, que poseen intereses disímiles (Bray & Tangney, 2017). Hay también argumentos más robustos que promueven la mediación de la tecnología para ofrecer nuevas alternativas para la construcción e interacción con el conocimiento matemático en contextos auténticos (Drijvers, Mariotti, Olive & Sacristan, 2010; Olive et al., 2010). A su vez, las tecnologías modernas pueden ayudar a aumentar la colaboración y a lograr un mayor énfasis en las aplicaciones prácticas de las matemáticas, a través del modelado, la visualización, la manipulación y la introducción de escenarios más complejos (Geiger, Faragher & Goos, 2010; Olive et al., 2010).
De este modo, la realidad tecnológica envuelve la práctica de enseñar y sus dispositivos se convierten en nuevos socios del contrato didáctico (Dagdilelis, 2018). En el escenario del aprendizaje de las matemáticas, las prácticas de los maestros no deben enfocarse en sitios comunes, como aquellos definidos por elementos estrictamente teóricos (Swain & Pearson, 2002), sino también en una variedad de enfoques de aprendizaje que incorporen materiales didácticos que motiven el interés y el gusto por aprenderlas (Arbain & Shukor, 2015). Otros lugares de enunciación pueden ser aquellos donde se introduzcan estrategias interactivas fundamentadas en tecnologías que aumentan y redimensionan el universo de métodos posibles para comprender, aún más, al sujeto que aprende (Skryabin, Zhang, Liu & Zhang, 2015). Este contexto posibilita la comprensión de la vinculación de la tecnología con el ejercicio pedagógico -y su papel central- (Tondeur, Forkosh-Baruch, Prestridge, Albion, & Edirisinghe, 2016), ya que promueve el avance del proceso educativo en medio de una gama de posibilidades frente a su implementación en el aula (Şad & Göktas, 2014), sobre todo cuando en algunos casos los docentes reclaman acciones de formación y actualización como alternativa para suscitar la innovación pedagógica.
La vinculación de la tecnología a la enseñanza de las matemáticas impone un desafío para el docente, no solo por el hecho de que las tecnologías digitales hayan transformado y estén transformando las relaciones humanas (Westera, 2004), sino también, porque esta vinculación parece servir de mediadora en la resignificación del proceso de enseñanza y aprendizaje (Inayat & Hamid, 2016). Se destacan dos perspectivas epistemológicas que pueden convivir en educación matemática: la primera concibe la tecnología como un recurso para el desarrollo de procesos de modelado; la segunda le asigna un rol reorganizador de este proceso, donde las tecnologías digitales son fundamentales para desarrollar experimentos y simulaciones que promuevan diversos tipos de participación de los estudiantes en la construcción de su propio conocimiento, al mismo tiempo que pueden acceder a soluciones numéricas, herramientas de visualización y control gráfico (Molina-Toro, Rendón-Mesa & Villa-Ochoa, 2019).
A favor de esta revolución, el software de geometría dinámica GeoGebra ha promovido nuevas formas de interacción en el aula -y fuera de ella- a partir del uso de recursos para el aprendizaje de las matemáticas (Arbain & Shukor, 2015). Aunque existe una gran variedad de resultados de investigación que evidencian una actitud positiva de los docentes frente a este tipo de recursos (Zakaria & Lee, 2012), se presenta un escenario paradójico que devela la integración precaria de software dinámico en los distintos niveles educativos, a pesar de un acceso creciente a las tecnologías digitales (Hohenwarter, Hohenwarter & Lavicza, 2009).
Desde esta perspectiva, resulta poco provechoso proponer la acción formativa sin tener en cuenta un proceso de alfabetización tecnológica que involucre tanto a docentes como a estudiantes (Schumann & Green, 2000). Este proceso de alfabetización, en el sentido de involucrar dispositivos móviles -como los teléfonos celulares- dentro y fuera del aula, es un tema crítico en la formación de maestros de hoy (Ozdamli & Uzunboylu, 2015), marcado por la interacción orgánica entre educación y tecnología que, particularmente, ha transformado la práctica educativa en relación con la enseñanza y el aprendizaje de las matemáticas (Taleb, Ahmadi & Musavi, 2015).
Hay evidencia empírica que valora las TIC como mediadoras en prácticas innovadoras en el aprendizaje de las ciencias (Kozma, 2014). En este sentido, aparece GeoGebra, un software que integra las posibilidades de la geometría dinámica y el álgebra computacional (Preiner, 2008) , como una herramienta para la educación matemática (Hohenwarter & Fuchs, 2004). Esta herramienta, que sirve para niveles o grados de enseñanza diferentes (Abramovich, 2013), ofrece nuevas oportunidades a partir de entornos tecnológicos, con fundamento en la visualización y exploración de objetos y conceptos matemáticos. Ha logrado marcar una pauta importante y diferenciadora en el ejercicio de enseñar matemáticas, además de estimular una percepción positiva por parte de los estudiantes que la usan y obtienen resultados de aprendizaje favorables (Arbain & Shukor, 2015). También, existe evidencia a favor del uso de GeoGebra para que los estudiantes exploren una gama más amplia de tipos de funciones y alcancen conexiones entre representaciones simbólicas y visuales (Dikovic, 2009) , incluso mayores, si se combinan con otras herramientas como los foros de discusión en línea (Zakaria & Daud, 2013) o el uso de pizarras digitales (Maclaren, 2014), con el ánimo de promover y transformar el discurso matemático.
La diversidad de recursos de GeoGebra facilita a estudiantes y maestros la enseñanza y aprendizaje de las matemáticas y es una herramienta valiosa para enfrentar los desafíos del mundo digital (Zakaria & Lee, 2012). Este software posibilita la representación de algunos procesos matemáticos desde una perspectiva geométrica y algebraica a la vez, en un entorno de fácil uso (Little, 2009). Así, GeoGebra aparece en el escenario educativo como un recurso que, si bien no resuelve por sí solo todos los problemas y dificultades del aprendizaje, sí plantea un salto cualitativo y tecnológico que pone a disposición del proceso educativo recursos, al transformar los límites y formas de aprendizaje (Fahlberg-Stojanovska & Stojanovski, 2009), que lo convierten en un recurso que propicia una transformación didáctica. En línea con este progreso, GeoGebra implementó, entre otras, dos aplicaciones móviles que han tenido una gran acogida: Calculadora Gráfica y Geometría. Esta apertura, que se enmarca dentro del contexto del mobile learning o m-learning, en el sentido del aprendizaje a través de contextos diversos e interacciones múltiples a través de dispositivos móviles, brinda la oportunidad de contar con los beneficios del software en estos dispositivos y poder aprender en cualquier momento y lugar, más allá del aula tradicional (Peng, Su, Chou & Tsai, 2009) y con una retroalimentación más afectiva que la tradicional, incluso para personas en condición de discapacidad (Georgiev, Georgieva & Smrikarov, 2004).
En algunos países, con un nivel de desarrollo importante, el aprendizaje mediado por dispositivos móviles se utiliza para apoyar y mejorar el aprendizaje tradicional y los enfoques de enseñanza, mientras que, en los países en vía de desarrollo, el difícil acceso a educación de calidad, condiciones económicas, sociales y políticas adversas y la falta de impulso a la innovación tecnológica en educación siguen siendo un impedimento que deja como resultado la poca investigación empírica sobre el tema (Hwang & Tsai, 2011; Pimmer, Mateescu & Gröhbiel, 2016). Otras investigaciones también han evidenciado los efectos positivos en la enseñanza del área bajo la curva y su relación con el valor de la integral definida cuando se incorpora la tecnología -en particular GeoGebra para PC-, como un instrumento de mediación en el proceso de aprendizaje (Tatar & Zengin, 2016).
El estudio de Caglayan (2016) busca superar las dificultades para comprender la esencia de la integral definida a través de las sumas de Riemann, la notación correspondiente y la generalidad involucrada en las expresiones. Para lograrlo, desarrolla actividades en el aula con apoyo de la tecnología, con el fin de ayudar a comprender este concepto y su relación geométrica con el área bajo la curva, y así lograr la comprensión del concepto de integral, definida de una manera fácil y directa. Allí se muestran evidencias de que algunos estudiantes ya estaban haciendo conjeturas sobre mejores aproximaciones y límites superior e inferior cuando la función estaba creciendo o decreciendo, para acercar de esta manera el valor de la integral mediante el área bajo la curva.
Otra experiencia significativa es la incorporación de GeoGebra en el proceso de enseñanza del concepto de área bajo la curva para estudiantes de secundaria que tuvieron una interacción inicial en el curso de cálculo integral, con el ánimo de lograr una mejor comprensión de los conceptos. Para ello, todos los estudiantes fueron provistos de un computador portátil que tenía instalada la versión de escritorio del software GeoGebra. En este contexto, se generaron construcciones que permitieron aproximar el área bajo la curva mediante sumatorias de áreas de rectángulos por defecto y por exceso para manipular los parámetros de función a integrar, número de rectángulos e intervalo de integración. De este proceso se pudo concluir que los estudiantes, al resolver problemas abiertos -diseñados para el uso en un entorno de aprendizaje respaldado por GeoGebra-, tienen una gran posibilidad de profundizar su comprensión de los conceptos del cálculo integral, tales como el área bajo la curva y su relación con la integral definida. Esto significa que el enfoque de aprendizaje se puede mover desde saber cómo resolver integrales hasta saber qué hacer y por qué (Mehanovic & Spikol, 2012).
Finalmente, este artículo pretende mostrar los resultados de investigación de un proyecto desarrollado en la Facultad de Ingeniería y Ciencias Básicas de la Fundación Universitaria Los Libertadores, cuyo propósito fue implementar una estrategia didáctica para la enseñanza de la noción de área bajo la curva, durante el desarrollo de un curso de cálculo integral, a partir de la integración de teléfonos celulares y de la aplicación móvil Calculadora Gráfica de GeoGebra, como dispositivos que pueden apoyar el proceso de aprendizaje -no como artefactos nocivos o distractores- y que responden a nuevas formas de reconocerse e integrarse a comunidades alternativas de aprendizaje.
Metodología
Se seleccionaron aleatoriamente noventa estudiantes de los programas académicos de Ingeniería Mecánica, Ingeniería Industrial e Ingeniería Aeronáutica, que cursaron cálculo integral. Se distribuyeron aleatoriamente en cuatro grupos según el diseño experimental 4G de Solomon (tabla 1). El 100% de los estudiantes contó con teléfonos celulares que se conectaron a internet a través del sistema de conexión inalámbrica proporcionado por la institución. A continuación, se presentan los rasgos relevantes de cada grupo:
Tabla 1 Composición de los grupos conformados para el experimento
| Grupo | Función | Cantidad | Edad promedio (años) | Pretest | Postest |
|---|---|---|---|---|---|
| 1 | Experimental | 23 | 20,2 | Sí | Sí |
| 2 | Experimental | 22 | 19,7 | No | Sí |
| 3 | Control | 21 | 20,1 | Sí | Sí |
| 4 | Control | 24 | 19,8 | No | Sí |
Fuente: elaboración propia.
El diseño general del experimento se dinamizó a partir de la metodología de cuatro grupos de Solomon, que consiste en un diseño experimental auténtico de pretest y postest (Solomon, 1949) que articula la experimentación en procesos de investigación, cuya principal virtud es controlar la reactividad de los instrumentos de medición (Whitman, Van Rooy, Viswesvaran & Alonso, 2008). Este diseño evita algunas dificultades conocidas y reportadas respecto a la validez interna del proceso experimental. También permite monitorear la naturaleza intrusiva de la prueba pretest en los resultados del postest y el efecto del tratamiento mediado por la aplicación móvil de GeoGebra en el número de respuestas correctas obtenidas en el postest. Estas dos variables son las que intervienen en el experimento y son analizadas a partir de distintas combinaciones que favorecen la consistencia de los resultados (Sawilowsky, Kelley, Blair & Markman, 1994).
El proceso inició con la identificación de qué evaluar: en este caso, los conocimientos previos sobre el cálculo de áreas -a través del pretest-, o posteriores -con el postest-, de los estudiantes en cuanto la noción de aproximación del área bajo la curva. Una vez identificados los conocimientos a evaluar, el siguiente paso fue formular las afirmaciones que permitieron dar cuenta del significado y alcance de los puntajes obtenidos por los estudiantes. A partir de cada afirmación se construyeron las evidencias; es decir, las acciones o productos observables que hicieron posible verificar los desempeños a los que se refieren las afirmaciones, por lo que las evidencias fueron la base para la construcción de las preguntas de las pruebas. El siguiente paso fue la elaboración de tareas, entendidas como enunciados que dan pautas para la construcción de las preguntas o ítems de una prueba y, de este modo, caracterizar la dificultad o complejidad de las preguntas.
Pruebas pretest y postest
Como instrumentos de pretest y postest se usaron pruebas estandarizadas de veinte preguntas de opción múltiple con única respuesta. Cada ítem tenía cuatro opciones de respuesta. Una era verdadera y las otras tres eran distractores. Los instrumentos se diseñaron a partir del diseño centrado en evidencias (Mislevy, Almond & Lukas, 2003), que pretende garantizar la validez a través de la articulación de los procesos y productos de los instrumentos con sus objetivos. Asimismo, se contó con la participación de los profesores expertos para la discusión acerca de los propósitos de la evaluación. De igual modo, participaron otros profesores en las mesas de discusión acerca de los propósitos de la evaluación de los conocimientos previos -pretest- o posteriores -postest- de los estudiantes que participaron en la intervención. Luego, acompañaron el proceso de validación de los instrumentos.
Después de identificar los conocimientos a evaluar (tabla 2), se construyeron las afirmaciones, que convierten el estándar en desempeños, para evidenciar el significado y el peso de los puntajes alcanzados por los estudiantes. Con base en cada afirmación, se levantaron las evidencias, es decir, los productos y acciones que facilitarían la verificación de los desempeños relacionados con las afirmaciones. Las evidencias recopiladas se asociaron con las actividades realizadas por los estudiantes con el ánimo de demostrar el desarrollo de competencias, conocimientos o habilidades. A partir de las evidencias, se inició la construcción de preguntas y, posteriormente, se prepararon los enunciados para la elaboración de los ítems correspondientes.
Interacción con la aplicación móvil Calculadora Gráfica
Se elaboraron dos unidades didácticas: una para los grupos control, que abordaron el concepto con calculadora científica tradicional; otra para los grupos experimentales, la cual incorporó la Calculadora Gráfica. A los grupos experimentales se les solicitó descargar la aplicación móvil a través de las diferentes plataformas existentes. Finalmente, se les pidió explorar la herramienta. Luego, comenzó la presentación del concepto de área bajo la curva a partir de la visualización que la Calculadora Gráfica permite. Una vez entendida la dinámica de la aplicación, se introdujeron diferentes parámetros para la estimación del área bajo la curva en una función determinada. Se utilizaron, entre otros, los valores n = 1 (figura 1), que supone una aproximación inicial; n = 2 (figura 2), que presenta una mejora en la aproximación inicial al incorporar un segundo polígono; y n = 5 (figura 3), que presenta una mejora sustancial respecto al área a ser estimada. Finalmente, con n = 25 (figura 4), es posible ver cómo el área se aproxima a partir de los polígonos regulares utilizados. La Calculadora Gráfica se destaca por la potencia y facilidad de la visualización de las curvas y polígonos, además del rápido cálculo numérico, lo cual facilita la presentación de la idea propuesta por Riemmann, y que puede considerarse como el sello distintivo del concepto de integral definida: el paso al límite de la sumatoria de Riemmann.
Resultados
Para el análisis de resultados, se tomó como variable dependiente de análisis el puntaje del pretest y del postest. La figura 5 presenta la distribución observada de los cuatro grupos y la relación entre ellos en términos de la presencia o ausencia del pretest y de la intervención.

Fuente: elaboración propia.
Figura 5 Distribución observada de los resultados en los cuatro grupos considerados.
En este punto, se considera pertinente hacer algunos comentarios desde una perspectiva enteramente descriptiva y exploratoria:
Estadísticamente la intervención tiene un efecto positivo en los grupos, pues los grupos 1 y 3 lograron mejores resultados que los grupos que no tuvieron la intervención con la herramienta propuesta.
Podría considerarse que el efecto del pretest en el postest en los grupos que no recibieron la intervención fue mínimo.
Podría conjeturarse inicialmente que sí existe un efecto del pretest en el postest en los grupos que sí recibieron la intervención, pues el grupo 3 -que no presentó pretest y tuvo la intervención mediada por la aplicación móvil- tuvo un mejor desempeño que el grupo 1 -que sí presentó pretest y también contó con intervención mediada por dicha aplicación-.
Para el análisis inferencial de los resultados, procedemos de acuerdo con Braver y Braver (1988), que plantean un flujograma para analizar la información recopilada con los cuatro grupos de Solomon. Para este caso, se descarta la influencia de la interacción, con una ANOVA de 2x2 con interacción, por lo que se procede a analizar los resultados con una ANOVA de 2x2 de efectos principales en el experimento -pretest e intervención-. La implementación computacional del estudio se realizó en el paquete estadístico R (versión 3.6.0), a través de la interfaz Rstudio (versión 1.2.1335), en un computador con sistema operativo Windows 10 Pro.
Tabla 3 Resultados de ANOVA de 2x2 de efectos principales sin interacciones

Fuente: elaboración propia
La tabla 3 presenta la salida principal del montaje de una ANOVA de 2x2 con efectos fijos. La figura 6 presenta una buena distribución de los residuos alrededor del intervalo de confianza -en azul- del 95% de confianza para los residuos. Además, el p-valor de la prueba de normalidad de Jarque-Bera para los residuos del mismo es 0.7467, lo que permite concluir la normalidad de los mismos.

Fuente: elaboración propia.
Figura 6 Distribución observada de los resultados en los cuatro grupos considerados.
La figura 7 presenta una buena distribución para los valores observados respecto a sus valores estimados, lo cual muestra que no existe evidencia de desviación de alguno de los supuestos del modelo general. De esta manera, con un nivel de significancia del 5%, hay evidencia estadísticamente significativa para afirmar que el modelo es válido.
Según la información de la tabla 3 y con un nivel de significancia del 5%, existe evidencia estadísticamente significativa para afirmar que la intervención mediada por la aplicación móvil tiene efecto en los resultados del postest. Por lo tanto, la intervención de GeoGebra fue importante para la comprensión de la noción de área bajo la curva para una función positiva, en el contexto de un curso de cálculo integral de la Facultad de Ingeniería y Ciencias Básicas de la Fundación Universitaria Los Libertadores.
De la misma forma, es posible afirmar que existe evidencia estadísticamente significativa en contra de la hipótesis de que el pretest no tiene efecto sobre los resultados en el postest. En otras palabras, la existencia de la prueba de entrada, condiciona los estudiantes durante su proceso de aprendizaje mediado por la aplicación Calculadora Gráfica sobre el estudio del área bajo la curva para la prueba de salida. Es decir, la experiencia del pretest condiciona la prueba de salida y no permite obtener resultados que sean clara y únicamente atribuibles a la intervención. De esta forma, además de resaltar el uso de las tecnologías en el aula como medio para facilitar el aprendizaje del cálculo, destacamos la importancia del pretest en el montaje de experimentos para verificar la eficacia de una estrategia didáctica particular.
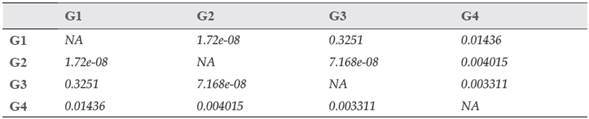
Para concluir las diferencias entre los grupos, la tabla 4 presenta los p-valores de pruebas t-student bicaudales entre los grupos para establecer las diferencias estadísticamente significativas entre ellas. Los grupos 1 y 3 tuvieron la intervención. El grupo 1 desarrolló el pretest, pero el grupo 3 no. En conclusión, la evidencia indica que el resultado del grupo 3 presenta una dinámica diferente a los demás grupos. Este grupo es el que tiene mejores resultados en la prueba.
Discusión y conclusiones
Se presentaron los resultados de investigación obtenidos de un diseño experimental que compara el logro académico alcanzado por dos grupos de estudiantes después de aplicar una unidad didáctica para la enseñanza de la noción de área bajo la curva a partir de la vinculación de la aplicación móvil Calculadora Gráfica de GeoGebra, frente al rendimiento de dos grupos de control que abordaron el tema de manera tradicional. El diseño mostró que la unidad didáctica que vincula a GeoGebra con los dispositivos móviles es pertinente para la enseñanza de dicho concepto en el contexto de estudiantes de ingeniería de la Fundación Universitaria Los Libertadores de Bogotá. Se necesitaron dos pares de montajes tradicionales del grupo control versus grupo experimental. Se consideró una prueba de entrada para uno de ellos únicamente. Este montaje permitió determinar la influencia de la intervención mediada por la aplicación móvil. Se consideró también la influencia de una prueba de entrada.
Los resultados señalan que, en los dos grupos que tuvieron la intervención mediada por la aplicación móvil, el rendimiento en la prueba de salida fue estadísticamente superior a los obtenidos por aquellos grupos que tuvieron una intervención tradicional -con calculadora científica tradicional- sobre la noción de área bajo la curva. Lo anterior ofrece evidencia estadísticamente significativa que sugiere la utilidad de la incorporación de las tecnologías digitales en las aulas -en este caso la aplicación Calculadora Gráfica- para la presentación de conceptos matemáticos. También, se tiene evidencia estadísticamente significativa de la influencia de la prueba de entrada en los resultados de la prueba de salida. Se consideró el hecho de haber presentado la prueba de entrada, más allá de la calificación obtenida en la misma. Lo anterior es un resultado fundamental para los autores, pues se deriva de la ejecución de este proyecto de investigación que tuvo como propósito analizar el efecto de una intervención mediada por una aplicación móvil. Se incorporó también la variable del desempeño en la prueba de entrada al momento de realizar el montaje del experimento.
De acuerdo con Bray y Tangney (2017), las herramientas tecnológicas también se utilizan para dar a los estudiantes nuevas formas de visualizar conceptos y abordar problemas de forma dinámica. Particularmente, en esta investigación se logró que un grupo de estudiantes visualizara geométricamente el concepto de suma de Riemann y, de esta manera, pudieran crear una noción de integral definida a partir de la manipulación de sumas de áreas de figuras geométricas, como rectángulos y trapecios, para aproximar el área bajo la curva determinada por una función f(x) y un intervalo de su dominio [a,b], y observar cómo se aproxima cada vez mejor el valor real del área cuando se incrementa el número de divisiones y se hace cada vez más pequeño el margen de error.
Los resultados de este proyecto de investigación deberían generar reflexiones profundas acerca de la validez externa de los experimentos de tipo pretest-intervención-postest con grupo control en educación matemática y la forma en que se construyen los experimentos para medir los efectos de estrategias didácticas -como la que aquí se presentó-, debido a que ese esquema parte de la hipótesis de que el pretest no es fuente de variabilidad para los resultados del postest. En este caso, esa hipótesis se rechaza debido a que se observó una influencia del pretest en la cantidad de respuestas correctas obtenidas en el postest.
Según Molina-Toro et al. (2019), los estudios futuros deberán centrarse no solo en múltiples herramientas tecnológicas o en el rendimiento de los estudiantes, sino también en cómo modelan, cómo dan sentido a sus conjeturas, cómo realizan sus experimentos, cuál es el impacto de las tecnologías digitales en ellos y cuáles son las características de las herramientas que seleccionan para abordar esos procesos. Aunque la literatura científica sobre m-learning se ha desarrollado recientemente, aún es escasa y se necesita más investigación teórica y empírica sobre el uso de dispositivos móviles en el modelado. Nuestros resultados pueden servir de insumo para avanzar en la comprensión de cómo los estudiantes dotan de sentido un objeto matemático a partir de la visualización y la interacción, como es en este caso, la noción de integral como área bajo la curva.