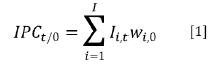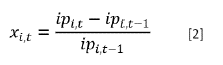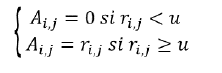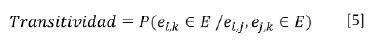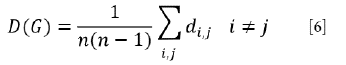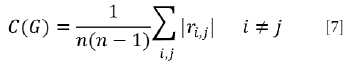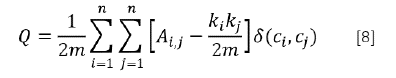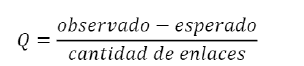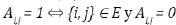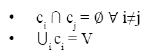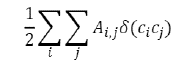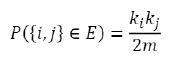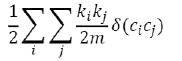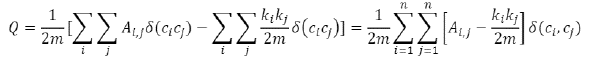INTRODUCCIÓN

En las economías de mercado, los precios de los bienes y servicios están sujetos a cambios constantes, por efecto de modificaciones en la oferta o la demanda. Algunos precios aumentan y otros disminuyen. Se habla de inflación cuando se produce un aumento generalizado de los precios. Como resultado, pueden adquirirse menos bienes y servicios por cada unidad monetaria y la moneda vale menos que antes. Concretamente, la inflación se define como el aumento generalizado y sostenido del nivel general de precios. Entre algunos de sus efectos, se destaca la pérdida sostenida del valor de la divisa que produce dificultades para ahorrar en moneda nacional y un desestímulo a la inversión real en detrimento de inversiones especulativas, que pueden terminar agravando aún más el problema.

Existen diversas teorías acerca de las causas de este fenómeno. Uno de los enfoques tradicionales para la comprensión de la inflación es la teoría monetarista. En ella, se supone que la inflación es esencialmente un fenómeno monetario que surge como consecuencia del desfasaje entre la oferta y la demanda de dinero. Cuando el Banco Central aumenta la cantidad de dinero (oferta) sin que exista una contrapartida en la demanda, esto provoca una disminución del valor de la moneda con lo cual se produce inflación. Dado que el enfoque anterior suele ser considerado de largo plazo, para comprender mejor la variación de precios en el corto plazo suele ser mejor enmarcarse en teorías keynesianas, vinculadas con las fricciones de corto plazo en los precios de los diferentes mercados analizados. Para una economía pequeña, abierta y altamente dolarizada como la uruguaya, es razonable suponer que la inflación dependerá de la evolución del tipo de cambio nominal, de la inflación del resto de mundo y de presiones internas.

Por otra parte, autores como ^{Noyola Vázquez (1956)} y ^{Olivera (1960)} han considerado que los modelos anteriores no son satisfactorios para describir la situación inflacionaria en países latinoamericanos. Por esto, plantean la teoría estructuralista de la inflación, donde se establece que la inflación surge como consecuencia de presiones básicas y de la puja distributiva entre distintos sectores y clases sociales de la economía. A diferencia de las teorías monetaristas y keynesianas, la inflación no se da por un exceso de demanda, sino por una rigidez en la oferta de bienes agrícolas, que, ante un aumento de la demanda, responde con un alza significativa de sus precios. De este modo, los aumentos de la cantidad de dinero son una consecuencia endógena de estos aumentos de precios. Esta teoría ve a las devaluaciones como un mecanismo redistributivo donde se da una transferencia de recursos desde los sectores industriales hacia los sectores agroexportadores.

En cambio, en ^{Heymann y Leijonhufvud (1995)} se sugiere que las causas de la inflación suelen ser más complejas que lo establecido por ciertos modelos tradicionales. El foco de la crítica que se hace a los modelos tradicionales es que no tienen en consideración el proceso de toma de decisiones de los empresarios y los motivos que llevan a decidir el aumento de precios. Los autores plantean abordar el comportamiento de los agentes desde una mirada más completa, entendiendo que el ser humano está inmerso en una sociedad sumamente compleja, con diversas instituciones (entre ellas el dinero) que hacen difícil abstraer y simplificarei comportamiento humano. Las personas toman sus decisiones de consumo y producción en este marco, dando lugar a interacciones entre los agentes y las variables del entorno. En este sentido, la economía puede ser vista como una red de contratos (formales e informales) inmersos en la estructura descrita anteriormente, y es así que puede entenderse a la inflación como un resultado emergente de este proceso.

Esta problemática conduce a que uno de los principales objetivos de los bancos centrales sea velar por la estabilidad de la moneda, es decir, mantener la inflación baja y estable en el tiempo. Este objetivo ayuda a crear un entorno predecible para la toma de decisiones, lo cual contribuye a suavizar los ciclos económicos y sentar las bases para un crecimiento sostenido del país. Los bancos centrales han basado el control de la inflación en políticas basadas en esquemas de metas de inflación (^{Taylor, 1993}; ^{McCallum, 1988}), donde se comprometen a estabilizar el aumento del nivel de precios a partir del ajuste de los instrumentos de política seleccionados y en respuesta a las condiciones macroeconômicas. Para que las políticas sean efectivas, los bancos centrales deben actuar de forma consistente, a la vez que las proyecciones sobre la economía y el comportamiento de los agentes económicos deben converger a las metas propuestas.

Cada familia tiene sus propios hábitos de consumo, que difieren de familia en familia. Las costumbres de consumo medios del conjunto de las familias determinan el peso de los distintos bienes y servicios en el cálculo de la inflación. En concreto, la inflación se calcula mediante la tasa de variación en el tiempo de un índice de precios, por lo general el índice de Precios al Consumidor, que mide los precios de una selección de bienes y servicios adquiridos por un consumidor medio. Por ejemplo, el índice Armonizado de Precio de Consumo mide la inflación de los precios de consumo en la zona del euro.

En Uruguay la inflación se estima con el índice de Precios del Consumo (IPC), un indicador agregado que estima la evolución mensual de los precios de un conjunto de bienes y servicios que consumen los hogares para un periodo y región determinados. Estos se seleccionan con base en su importancia relativa en el gasto total y la frecuencia de hogares que consumen estos bienes. El IPC se calcula de la siguiente manera:

Donde f es el subíndice que representa a cada uno de los bienes y servicios, IPC_t/0 es el índice de precios del consumo en el periodo t, con base en el periodo 0, I _it .es el índice de precios del producto í en el periodo t, y w. _i,0 es la ponderación del producto i en el mes base (periodo 0). Nótese que -además de medir las variaciones de los precios a nivel del consumidor-, el IPC se utiliza para calcular el poder adquisitivo de la moneda, calcular el índice de salario real y sirve como deflactor de las cuentas nacionales.

Si bien este índice permite tener una estimación de la inflación en distintos plazos, existen ciertos inconvenientes asociados a su construcción. Uno de los principales problemas es que al usar una canasta de bienes y servicios consumidos por un tipo de familia determinada que se mantiene constante en el tiempo, no se contempla la sustitución de bienes ante cambios en los precios relativos que podrían realizar los consumidores. A su vez, tampoco considera cambios en la calidad de los bienes, en la estructura de consumo o en la relación entre los distintos bienes y servicios, y tampoco contempla la introducción de nuevos bienes. Por estas razones, cada cierto periodo se procede a una actualización de la canasta, también conocida como cambio de base. La construcción del IPC se hace mediante una encuesta sobre gastos familiares obtenida a partir de una muestra significativa de toda la población¹.

Este trabajo pretende ofrecer una mejor comprensión de las características de la inflación, abordando al sistema de precios de la economía como un sistema complejo. Si bien en este trabajo el ejercicio se realiza para el caso de la economía uruguaya, puede extenderse a cualquier otro país. El estudio introduce técnicas de análisis innovadoras que permiten comprender en mayor medida las características del fenómeno. Por ello, nuestros objetivos consisten en estudiar la relación entre las redes de precios y la inflación, analizando la relación entre los periodos de inestabilidad macroeconômica con cambios en la estructura de la red. En particular, se observará cómo evoluciona la red ante variaciones en la política cambiaria.

Asimismo, poder relacionar el resultado del sistema (nivel de inflación] con lo que ocurre a una escala meso (visualizado a partir de redes de precios) puede dar lugar a una mejor comprensión del fenómeno, ya que se pueden estudiar los procesos internos del sistema que dan lugar a cambios en el nivel de precios. Además, podrían identificarse distintas fases del proceso inflacionario con base en la composición interna de las redes para distintos niveles de inflación, lo cual daría lugar a detección de umbrales o puntos de quiebre donde la dinámica del sistema cambie radicalmente.

Es preciso destacar que, dado que estaremos enmarcados en la teoría de los sistemas complejos, este trabajo no buscará hacer predicciones acerca de la inflación (^{Edmund, 2017}), sino que se propone un modelamiento explicativo. Con base en esto, será posible obtener una mayor comprensión acerca de la estabilidad de los precios relativos y la respuesta a shocks devaluatorios.

El documento se estructura de la siguiente forma. En la sección posterior se hace una revisión de antecedentes. Luego se describe el proceso de obtención y procesamiento de los datos, mientras que en una sección siguiente se detalla la metodología utilizada para analizar los datos. Posteriormente se presentan los resultados empíricos, y en la sección final se presentan comentarios, conclusiones y posibles extensiones de este trabajo.

ANTECEDENTES

Existen algunos trabajos académicos que estudian la inflación en Uruguay desde el punto de vista de la descripción y predicción del fenómeno. Un precursor de esta línea es ^{Cancelo et al. (1994)}, que analiza el proceso inflacionario dividiendo los bienes y servicios que lo componen en transables y no transables; se constatan diferencias entre las dinámicas de las series, por lo que se realiza una proyección desagregada del IPC con base en esta categorización. Es importante destacar que la distinción entre ambos tipos de bienes es efectuada de forma ad hoc por los autores, sin basarse en un método estadístico. Sin embargo, esta elección no es arbitraria ni trivial, sino que existen diversos modelos económicos (^{Samuelson, 1964}) que sugieren que es esperable que las dinámicas de los bienes transables y no transables sean distintas, ya que están sujetas a diferentes procesos de producción. Asimismo, ^{Garda et al. (2004)}, ^{Cuitiño et al. (2010)} y ^{Brum et al. (2012)} realizan mayores desagregaciones para efectuar las predicciones, que pueden coincidir o no con las divisiones del IPC.

Dado que Uruguay es una economía pequeña y abierta, es esperable que el tipo de cambio nominal sea una variable relevante en la determinación de precios, y dada la creciente integración económica, se espera que aumentos del tipo de cambio sean cada vez más influyentes. De hecho, ^{Licandro (2000)} estima que un aumento de un 1% en el tipo de cambio nominal genera un aumento de un 0,83% en el IPC. En otro trabajo, ^{Zacheo y Güenaga (2019)} constatan que la magnitud del impacto de una devaluación en los precios se encuentra vinculada con las expectativas de los agentes económicos con respecto a la credibilidad de las metas de inflación. El estudio evidencia una reacción más fuerte ante shocks del tipo de cambio cuando las expectativas están desalineadas.

En alternativa a los trabajos anteriores, ^{Alvarez et al. (2021)} analizan el sistema de precios de Uruguay como un sistema complejo; constatan que para el periodo de estudio existe un proceso evolutivo en el sistema de precios, caracterizado por la dinámica no constante en la composición de las comunidades de precios. Al intentar encontrar una estructura de comunidades representativa del periodo, es determinante el grado en que los bienes y servicios son sujetos de intercambio comercial con otros países. Esto da un sustento inicial para justificar que la dinámica de las comunidades de los bienes depende de esta característica, pero no permite concluir que esto se sostenga a nivel micro.

El trabajo de ^{Brum et al. (2016)} constituye un estudio desde la perspectiva monetarista de la inflación para lograr una mejor comprensión de este fenómeno a largo plazo. En él se constata la existencia de un "impacto positivo y significativo del crecimiento del núcleo monetario en la tasa de inflación", donde al realizar pruebas de significación estadística se concluye que la trayectoria de la inflación está pautada por el crecimiento de la base monetaria por encima del crecimiento de la demanda de dinero. Luego, estudios de corte keynesiano han sido utilizados para comprender en mejor medida las dinámicas cortoplacistas de la inflación. Estos pueden ser complementados con el enfoque de ^{Álvarez et al. (2021)}, que también es de corto plazo y permite visualizar otros aspectos del fenómeno, aunque la literatura adolece de estudios que complementen ambos enfoques. Por último, siempre se han hecho predicciones desde un enfoque econométrico para predicciones a corto y mediano plazo, aunque podría ser interesante incorporar otras técnicas estadísticas, tales como redes neuronales (ver ^{Sari et al., 2016}) para la predicción.

Con respecto a los antecedentes académicos del estudio del fenómeno inflacionario desde la perspectiva de los sistemas complejos, además del trabajo anteriormente descrito, se han encontrado dos referencias: ^{Gao et al. (2013)} para el caso de China y ^{Sarantitis et al. (2018)} para el Reino Unido. En ^{Gao et al. (2013)} se construye una red compleja tomando como nodos distintos precios de la economía y como aristas la correlación entre estos. Dado que la correlación empírica entre dos series nunca es exactamente 0, lo que daría lugar a redes excesivamente densas, se utilizó un umbral u = 0,82 para filtrar todas las correlaciones que estuvieron por debajo de este valor. En cuanto al Reino Unido, se realiza el mismo procedimiento que el caso anterior, pero incluyendo solo bienes y servicios que componen el IPC y tomando un umbral de u = 0.5. En lo que respecta a Uruguay, como se comentó previamente, existe el antecedente de ^{Álvarez et al. (2021)}, que al igual que el caso de ^{Sarantitis et al. (2018)} construye redes complejas con base en las clases del IPC, pero tomando un umbral de u = 0,36.

A pesar de la importancia de comprender la dinámica del proceso inflacionario, no hemos encontrado otros trabajos que se refieran al caso de Uruguay o sobre la aproximación al problema desde los sistemas complejos. La escasez de estudios académicos del tema abre la posibilidad a desarrollar ulteriormente el análisis del caso uruguayo y de otros casos desde la perspectiva de la economía de la complejidad.

DATOS Y METODOLOGÍA

Datos

Los datos primarios utilizados como base de este trabajo fueron extraídos de la base del índice de Precios del Consumo (IPC), el cual es elaborado por el Instituto Nacional de Estadística (INE) con frecuencia mensual. Se tomaron datos comprendidos en el periodo marzo de 1997 hasta julio de 2020, aunque cabe aclarar que la base está subdividida en dos periodos (marzo 1997 a noviembre 2010 y diciembre de 2010 en adelante), ya que en diciembre de 2010 se realizó un cambio de base.

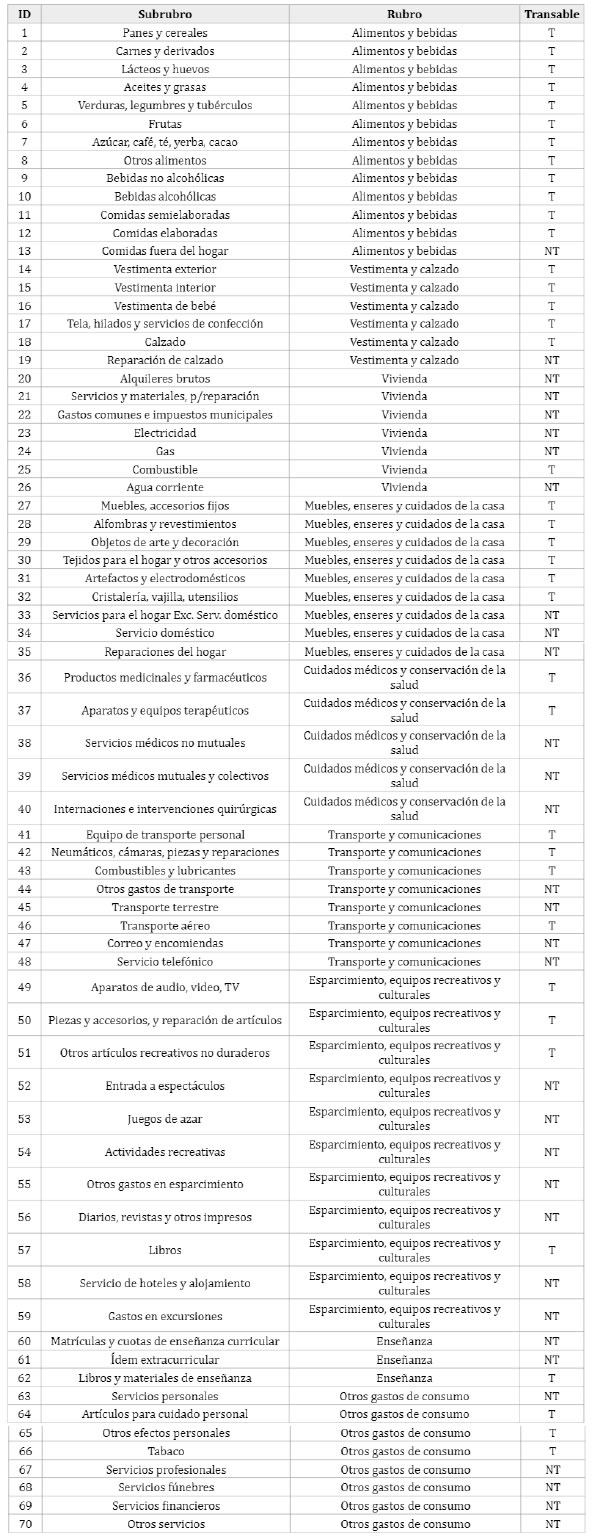
Los datos correspondientes al primer periodo tienen como base el mes de marzo de 1997, en el cual se introdujo un cambio metodológico (véase ^{INE, 1997}) con respecto al periodo que le precede. En esta ocasión, el IPC estaba compuesto por 310 bienes y servicios correspondientes al área urbana de Montevideo, los cuales se pueden agrupar a distintos niveles en conjuntos de bienes y servicios considerados similares, conformándose 70 subrubros y 9 rubros que engloban a los primeros. Para este trabajo se utilizará el nivel de desagregación correspondiente a los subrubros (véase Anexo A.1), por lo cual se disponen de 70 series temporales.

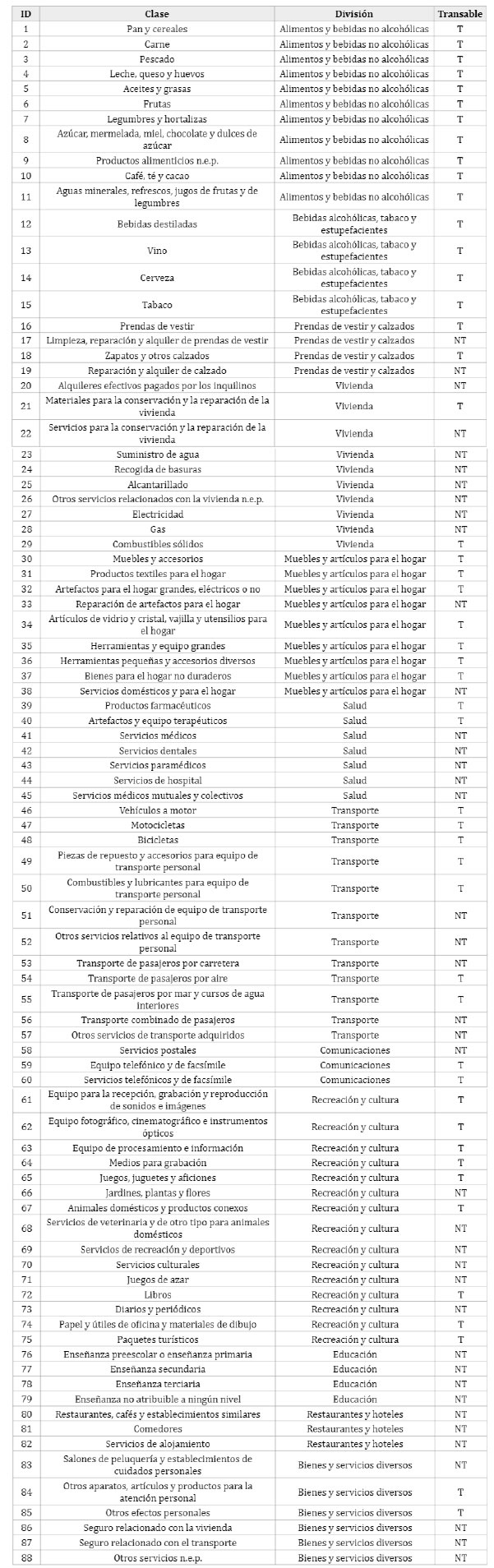
El segundo periodo tiene como base el mes de diciembre de 2010, donde no solo se amplía la cantidad de bienes y servicios considerados a 374 (véase ^{INE, 2010}), sino que también se incorporan a la muestra algunas áreas urbanas del interior del país, por lo cual este índice representa la evolución del precio de una canasta de consumo típico de una familia de Montevideo o del interior urbano. Estos productos se agrupan en 88 clases de bienes y servicios con características similares, las cuales a su vez se agrupan en 12 divisiones. Así como en la primera parte se consideró el nivel de los subrubros, para este periodo se tomaron los datos correspondientes a las clases (véase Anexo A.2), disponiéndose de 88 series temporales. El formato con el cual se trabajan las series es el de las variaciones mensuales porcentuales para cada una de las clases o subrubros. Por lo tanto, a cada serie ip _i , _t en el momento t se la transforma (ecuación [2]) para obtener una nueva serie temporal X_it,... Obsérvese que al realizar dicho procedimiento se "pierde" una observación para cada uno de los dos subperiodos.

Análisis de redes

Definición

Se define una red compleja como una red (modelada como grafo) que posee ciertas propiedades estadísticas y topológicas no triviales, características de los sistemas complejos que no ocurren en redes simples. Una red (o grafo) es un conjunto de objetos llamados nodos (vértices) unidos mediante enlaces llamados aristas (arcos), que sirven para representar relaciones entre elementos de un conjunto. La definición precisa de red es la siguiente: se define una red G (V, E) como un conjunto de nodos (V) relacionados entre sí a partir de aristas (E). El conjunto de nodos V = {v _1, v ₂ ,…v _n } representa los objetos a estudiar, mientras que el conjunto de aristas E = {e _1.1, e _1,2 ..., e _n,n } da la conexión entre los distintos nodos de la red, donde se cumple que el nodo í está conectado con el nodo; si y solo si e_ij ЄE (o análogamente, {i,j} ЄE).

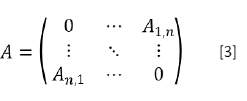
Un grafo puede ser representado a partir de una matriz de adyacencia A_nxm (ecuación [3]), donde el elemento A _i,j , representa el enlace que une al nodo í con el j. En el caso de que dos nodos no estén conectados, se indica con un 0 en la matriz de adyacencia, por lo que A_i,j. = 0 ⇔ {i,j} ∉ E; los valores diferentes a 0 implican que existe un enlace entre ambos nodos, y el elemento A_i,j de la matriz nos da la intensidad de dicho vínculo. En este trabajo se utilizan redes no dirigidas, esto quiere decir que la relación entre el nodo i y el nodo j es la misma que la relación entre el nodo j y el nodo z; y sin autobucles, esto quiere decir que no existe relación del nodo i consigo mismo. En términos de la matriz de adyacencia, estas condiciones pueden expresarse como A_i,j. = A_i,j y A_i,j = 0, respectivamente, por lo que la matriz de adyacencia será una matriz simétrica con la diagonal principal nula.

Construcción de las redes

Para este trabajo los nodos estarán representados por los subrubros (para el periodo marzo 1997 a noviembre 2010) y por las clases (para el periodo diciembre de 2010 a julio de 2020), por lo que para el primer periodo las redes tendrán 70 nodos, mientras que para el segundo tendrán 88. Esto hace que las redes no sean estrictamente comparables entre los dos periodos debido a la heterogeneidad en la composición de los nodos.

Estas redes serán construidas utilizando datos correspondientes a periodos de 12 meses, desde una ventana temporal mensual a fin de poder obtener la mayor cantidad de redes posibles. Para la construcción de estas redes se utilizó el paquete igraph (^{Csárdi y Nepusz, 2006}) del software estadístico R. A modo de ejemplo, la primera red será construida usando los datos comprendidos entre marzo de 1997 y febrero de 1998, la segunda con datos entre abril de 1997 hasta marzo de 1998, y así sucesivamente. Es importante destacar que dentro de cada periodo los nodos se mantienen constantes y lo que se modifica son las aristas, ya que estas dependen de la correlación entre las clases o subrubros, que a su vez van evolucionando a medida que se mueve la ventana temporal.

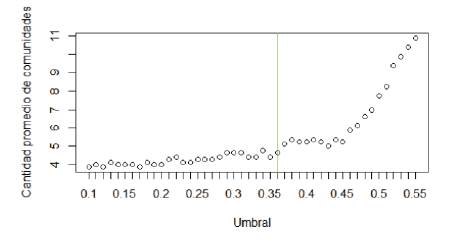
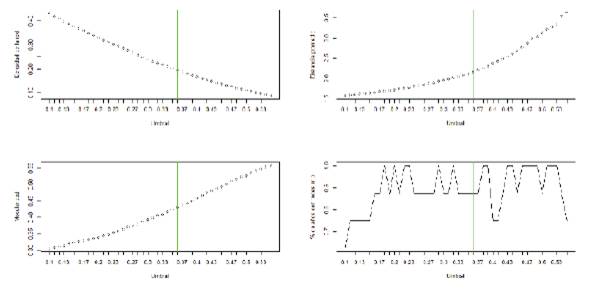
En ambos casos, las aristas entre los nodos estarán representadas por el coeficiente de correlación lineal de Pearson en el periodo de construcción de la red entre las clases o subrubros que representan a cada nodo. Como fue señalado, este valor representa la intensidad del vínculo entre dos elementos de la red. En términos de la matriz de adyacencia, esto puede ser representado como A_i,j =A.. = por lo que en principio se establecerá que dos nodos estarán conectados si tienen una correlación distinta de 0. Esta situación puede dar lugar a redes excesivamente densas donde se toma como válida información poco relevante que puede llegar a resultar en conclusiones erróneas. Basándonos en antecedentes previos (^{Sarantitis et al., 2018}; ^{Álvarez et al., 2021}), se procederá a filtrar todas las correlaciones por debajo de cierto umbral u. Para el caso de Uruguay, el antecedente de ^{Álvarez et al. (2021)} establece como valor de umbral u = 0,36 (véase Anexo A.3). Por lo tanto, la matriz de adyacencia de la red que estudiamos A_nxm está determinada por:

Una vez realizado este procedimiento, se obtienen 154 redes de 70 nodos para el primer periodo y 104 redes de 88 nodos para el segundo periodo, por lo cual es posible comenzar su análisis.

Densidad de ¡a red

La densidad de la red G, denotado den[G) (ecuación [4]), representa el grado de conectividad entre los nodos de la red. Toma valores entre 0 y 1, siendo 0 una red donde no existen conexiones entre los distintos nodos y 1 donde todos los nodos están conectados entre sí. Se define como el cociente entre la cantidad de aristas existentes y la cantidad máxima de aristas posibles, donde, para el caso de una red no dirigida y sin autobucles con n nodos, es de n(n - 1)/2.

Transitividad

Este indicador busca cuantificar qué tan cierto es que si el nodo i está relacionado con el j, y el j con el k, esto implica que el nodo ¡ está relacionado con el k. En términos precisos, podemos dar la siguiente definición: dados tres nodos i,j y k, donde e_i,j Є E y e _j,k Є E, una transitividad de 1 implica que necesariamente e _j,k Є E, mientras una transitividad de 0 implica que e _j,k ∉ E. En particular, este indicador (ecuación [5]) se puede interpretar como la probabilidad de que e _j,k Є E, dado que e _i,j Є E y e _j,k Є E.

Distancia promedio de la red

La distancia entre dos nodos dentro de una red se define como la longitud del camino más corto que une a dichos nodos. La distancia promedio de la red G, denotado D(G) (ecuación [6]), es la distancia promedio entre dos nodos cualesquiera. Permite cuantificar qué tan rápido fluye la información dentro de la red y para su cálculo no se tiene en cuenta el peso de las aristas, es decir, .

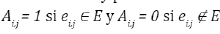Correlación media de la red

Permite analizar el grado de correlación de la estructura de precios de la economía para los distintos periodos de análisis. Para su cálculo, es necesario trabajar con todas las correlaciones, es decir, se trabajan con los datos sin filtrar. Se define la correlación media de la red G, denotado C(G), que se calcula con la siguiente fórmula:

Comunidades

Detectar comunidades permite identificar subgrupos de precios con dinámicas similares dentro de las redes a estudiar. Para este trabajo se utilizará el algoritmo de Louvain propuesto por ^{Blondel et al. (2008)}. Es un algoritmo del tipo "jerárquico agregativo" (aunque con ciertas particularidades) que tiene como fin detectar comunidades de nodos con gran cantidad de enlaces entre ellos y pocos enlaces entre los nodos de diferentes comunidades. Con este fin, se busca maximizar la modularidad Q (ecuación [8]), la cual toma valores en el intervalo [-1, 1], donde valores próximos a 1 indican que existe gran cantidad de enlaces dentro de las comunidades en comparación con la cantidad de enlaces entre comunidades.

Donde n es la cantidad de nodos en la red; A., representa el enlace que va desde el nodo i al nodo 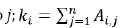es el grado del nodo i; 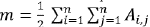es el valor total de los enlaces en la red; c. es la comunidad del nodo i; y δ(c _i , c _j ) es la delta de Kronecker: la cual vale 1 si c_i = c _j y 0 en caso contrario. Una derivación matemática de la intuición que está detrás de esta expresión se encuentra en el Anexo A.4.

El algoritmo se aplicará tantas veces como redes se tengan; por lo tanto, para cada periodo es posible obtener la modularidad como medida representativa de la calidad de las comunidades, así como la cantidad de comunidades que se obtuvieron, e incorporarlas al análisis junto con los demás indicadores.

RESULTADOS DEL ANÁLISIS DE REDES

Como se ha mencionado, se construyeron redes para los diversos años de estudio usando ventanas móviles de un mes. A fin de ilustrar los resultados obtenidos, la figura 1 representa las redes de precios obtenidas para los periodos diciembre de 2002 y 2014. En ella puede observarse que en ambos casos (y en los casos no visualizados) existe un conjunto de nodos centrales rodeados de otros periféricos, donde los primeros se caracterizan por haber tenido una dinámica similar a muchos otros nodos de la red en su periodo de construcción, mientras que los segundos tuvieron un comportamiento atípico. Si bien esta estructura se mantiene para todas las redes, los resultados en términos de las redes per se son sumamente dinámicos: se observa que la posición y el comportamiento de los nodos cambia a lo largo del periodo de estudio.

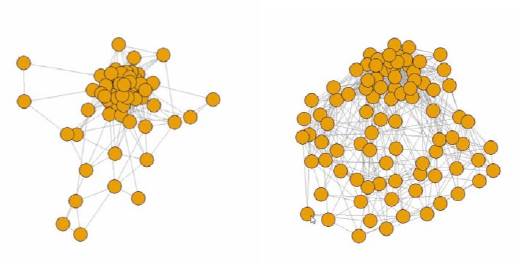
Fuente: elaboración propia a partir de datos del Instituto Nacional de Estadística de Uruguay (INE).

Figura 1 Redes de precios de ¡a economía uruguaya a diciembre de 2002y 2014, respectivamente 

Para abordar esta sección del análisis se estudiará por separado lo sucedido en el periodo 3/1997-12/2010 y 1/2011-7/2020. Esto se debe a que, al realizarse el cambio de base en el IPC en diciembre de 2010, las redes no son comparables debido al cambio en la cantidad de nodos (redes de distinto tamaño). Asimismo, es preciso aclarar que en términos de la evolución de los indicadores no se disponen datos en los periodos 3/1997-2/1998 y 1/2011-11/2011, ya que estos periodos fueron necesarios para la construcción de las redes.

La figura 2 muestra las correlaciones entre los diferentes indicadores seleccionados y la inflación interanual, donde el color rojo está asociado con correlaciones altas y positivas, el azul con altas y negativas, y el blanco con correlaciones débiles. Con respecto al primer periodo, en términos generales se observa que la inflación interanual presenta correlaciones fuertes con varios indicadores de la red. En particular, la inflación interanual registra una correlación alta y positiva con la densidad de la red, la transitividad y la correlación media, mientras que presenta una correlación alta y negativa con la distancia promedio y la modularidad.

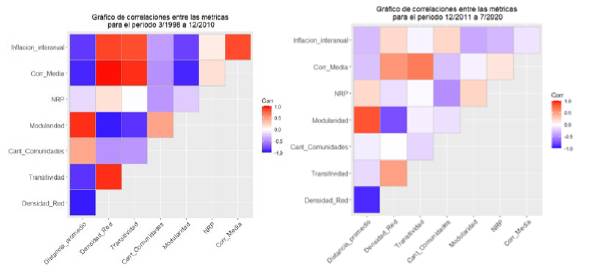
Fuente: elaboración propia a partir de datos del Instituto Nacional de Estadística de Uruguay (INE).

Figura 2 Correlaciones entre la inflación y los distintos indicadores para el primer y segundo periodo de estudio, respectivamente 

Al estudiar las correlaciones entre los distintos indicadores, se encuentran varios resultados esperables, como una correlación alta y positiva entre la densidad de la red y la correlación media (lo cual es esperable debido a la forma en la que se construyeron los enlaces), una correlación alta y positiva entre la correlación media y transitividad, y correlaciones negativas entre la densidad de la red y la distancia promedio.

Sin embargo, es importante destacar que en este periodo de estudio ocurrió en Uruguay una crisis económica que tuvo, entre otras consecuencias, una fuerte devaluación dela moneda (ladevaluación interanual fue de 112% en agosto del 2002), con las ya mencionadas consecuencias para el nivel general de precios. Basados en los postulados de la teoría de inflación de costos y en constataciones empíricas para Uruguay (^{Cancelo et al., 1994}; ^{Bergara et al., 1995}), se puede afirmar que una devaluación de la moneda provoca transmisión al nivel general de precios por la vía de aumento de costos de producción para los productores locales y por vía del aumento de los precios de los bienes transables que están sujetos a lo que sucede en el resto del mundo.

Como mencionan ^{Coleman et al. (2010)} y ^{Mordecki (2018)}, en el 2002 se desencadena una profunda crisis económica con caída del PIB superior al 10%, con consecuencias en la desigualdad y los niveles de pobreza. Previamente a esta crisis, durante la década de 1990 se estableció un plan de estabilización con ancla cambiaría, en un contexto de reformas estructurales importantes en Uruguay y la región. En esos años, las reformas apuntaban a una mayor "disciplina fiscal y monetaria, en conjunto con la liberalización, desregulación, apertura externa y privatización de la economía" (^{Mordecki, 2018}).

Por lo tanto, y con el fin de realizar un análisis más detallado, se dividió este periodo en tres etapas: un periodo precrisis comprendido entre marzo de 1998 y mayo de 2002; el periodo de crisis está comprendido entre junio de 2002 y enero de 2004; mientras que el periodo poscrisis se corresponde a febrero de 2004 y diciembre de 2010. Cabe destacar que la selección de estos periodos se realizó con base en los problemas inflacionarios (no necesariamente económicos), tomando como registros críticos aquellos en los cuales la inflación superó el 10%. La elección del punto de quiebre se hizo considerando lo establecido en la "cláusula gatillo", donde se pauta que, en caso de que la inflación supere un 12%, los salarios nominales deberán ajustarse para evitar que los trabajadores pierdan salario real. Si bien nuestro valor difiere del establecido en la cláusula, se elige el 10% ya que es un valor que se encuentra lo suficientemente cerca y, además, es el primer valor que alcanza las dos cifras. Esto tiene implicancias desde el punto de vista psicológico para los agentes, ya que perciben fácilmente que el sistema probablemente se empiece a comportar de manera distinta. Es importante notar que este valor es adecuado para la situación uruguaya, pero no asegura que sea extrapolable a otros países².

Al analizar el periodo de crisis, parece observarse en la figura 4 que la inflación interanual estaría fuertemente vinculada con lo que sucede dentro de las redes, y se nota una alta correlación entre los distintos indicadores y la inflación. En cambio, en los periodos de estabilidad no se observa una relación tan intensa entre los indicadores y la inflación, aunque en líneas generales se observa una mayor correlación para el periodo poscrisis. Esto podría indicar que los efectos de la crisis tuvieron un impacto en la estructura de las redes.

Dado el marco teórico planteado, podría pensarse este resultado como una consecuencia de que la inflación sería un sistema de dos fases, donde las inflaciones altas y bajas conllevan dinámicas sustancialmente distintas en cuanto al proceso de formación de redes de precios. En el mismo sentido, podría pensarse en la existencia de un umbral para la inflación cercano al 10 %, a partir del cual la dinámica del proceso cambia rotundamente.

Otro de los resultados destacables es la fuerte relación entre la cantidad de enlaces y los periodos de alta inflación. Se observa que en los periodos de estabilidad la correlación entre ambas variables es inferior a 0,3, mientras que en los periodos de crisis inflacionaria la correlación es de 0,78. Esto nos permitiría concluir que los periodos de crisis generan una ruptura en la estructura de precios relativos de la economía, ya que surge un gran número de altas correlaciones entre precios. A su vez, esto puede ser visto como un aumento en el flujo de información entre diferentes precios, ya que, al haber más aristas, la información fluye de manera más ágil dentro de las redes.

Al considerarse el último periodo de los datos (2011 en adelante), se tiene que las correlaciones son más débiles (figuras 2 y 5) que antes y se constatan cambios en el sentido de la correlación entre algunos indicadores y la inflación. Esto podría deberse a que estamos enmarcados en un periodo de inflación estable (similar a los periodos de pre- y poscrisis), por lo cual se mantienen los resultados de correlaciones débiles ante inflaciones bajas.

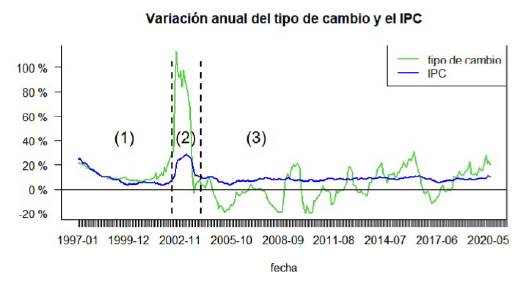
Fuente: elaboración propia a partir del Instituto Nacional de Estadística de Uruguay (INE).

Figura 3 Comparación de la evolución interanual del tipo de cambio y el aumento de precios en el periodo enero de 1997 a junio de 2020, separado por etapas 

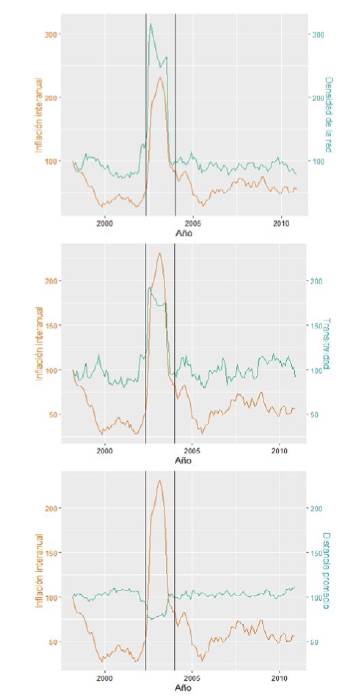
Fuente: elaboración propia a partir de datos del Instituto Nacional de Estadística de Uruguay (INE).

Figura 4 Comparación de principales indicadores con la inflación interanual en el periodo marzo de 1997 a diciembre de 2010, separado por etapas (índice en marzo de 1998 = 100) 

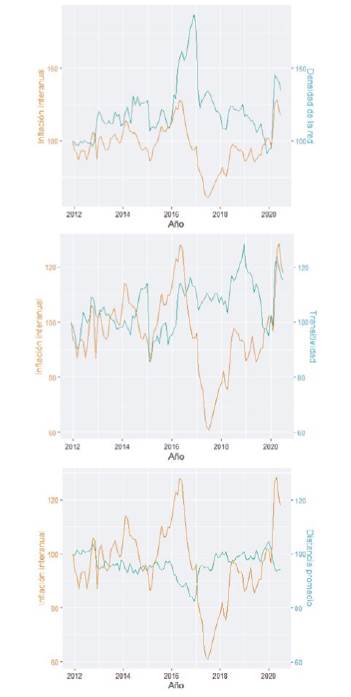
Fuente: elaboración propia a partir de datos del Instituto Nacional de Estadística de Uruguay (INE).

Figura 5 Comparación de principales indicadores con la inflación interanual en el periodo diciembre de 2011 a julio de 2020, separado por etapas (índice en diciembre de 2011 = 100) 

Sin embargo, se sigue manteniendo el hecho de que los picos de inflación están asociados a cambios en la topología de la red. En este caso, se observa que tanto la densidad de la red como la transitividad aumentan significativamente en los momentos en los que la inflación alcanza los valores más altos dentro de este subperiodo (fines de 2016 y principios de 2020), los cuales, nuevamente, superaron el mencionado umbral de 10%. Es interesante notar que estos picos inflacionarios estuvieron relacionados con aumentos importantes en el tipo de cambio, como puede apreciarse en la figura 3. Por lo tanto, estos resultados sugieren que variaciones importantes en el tipo de cambio generan disrupciones en la topología de la red, formándose grupos más cohesivos asociados a la distinción entre las dinámicas de bienes transables y no transables.

Esto parecería indicar que, para este periodo de estudio, se constata una relación entre el comportamiento del sistema a un nivel macro (vista desde la inflación) y de las redes expresada a través de los indicadores. Por lo tanto, se observa que, en periodos de estabilidad del sistema de precios, las redes también presentan un comportamiento estable. Asimismo, esta relación se mantiene en periodos de inestabilidad: se constatan cambios abruptos en la topología de las redes en momentos de fluctuaciones intensas de precios; es decir, se encuentra una relación entre el comportamiento del sistema a un nivel meso y el output del sistema.

Los resultados obtenidos de la relación entre los indicadores de red y la inflación interanual son consistentes con los obtenidos para el Reino Unido en el trabajo de Garantitas et al. (2018). En periodos de estabilidad (gran parte del periodo considerado para el trabajo en el Reino Unido) se encuentra una relación débil entre ciertos indicadores propuestos por los autores y la inflación. Por otra parte, ante un aumento abrupto en la inflación en el periodo de 2008-2009 (crisis financiera), también constatan la existencia de un pico en la densidad de la red.

Lo mencionado es concordante con lo expuesto por ^{Caraballo y Dabus (2008)}, autores que encuentran una relación entre la inflación y la variabilidad de los precios relativos (vista, en nuestro caso, desde la evolución de las redes). A su vez, los autores constatan que los diferentes regímenes de inflación son determinantes en la variabilidad de precios, lo cual coincide asimismo con los hallazgos de este trabajo. Esto tiene consecuencias para la asignación de recursos por parte de los agentes. Entendiendo al sistema de precios como el resultado de las interacciones entre individuos y como base de las decisiones futuras de estos, cambios abruptos en el sistema y en la estructura de precios relativos hacen que la asignación óptima de dichos recursos sea difícil.

CONCLUSIONES

El presente trabajo permitió abordar la estructura de precios de la economía uruguaya desde un enfoque no tradicional, como lo son los sistemas complejos. Como resultado, se vieron características del sistema que serían difíciles de percibir si se buscaran mediante los métodos usuales desde los cuales se ha abordado la inflación en Uruguay.

En particular, se pudo comprobar que para el periodo de estudio el sistema se comporta sustancialmente distinto durante periodos de inestabilidad. Este resultado no es algo nuevo en la teoría económica (^{Blanchard, 2014}), sino que debería ser considerado por parte de los hacedores de política y agentes económicos. Por lo tanto, quienes realizan modelos deben ser precavidos con estos cambios de fase que se pueden producir en el sistema, ya que un modelo puede operar de forma adecuada si el sistema mantiene su comportamiento; pero en caso de que se produzca un cambio de fase y la dinámica del sistema se transforme rotundamente, los modelos darán resultados erróneos (tal como ha sucedido en el pasado).

Es preciso recordar que un proceso inflacionario puede darse como un aumento del nivel general de precios sin cambios sustanciales en la estructura de precios relativos, o con cambios bruscos en estas relaciones. El segundo caso suele ser más nocivo para la economía ya que el aumento de precios no solo erosiona los saldos en moneda nacional, sino que también cambia la forma en la cual los agentes asignan sus recursos, ya que, ante cambios en los precios relativos, se generan incentivos a la relocación de factores productivos y cambios en la estructura de consumo. Pudo observarse que durante los procesos de alta inflación aumentaba la densidad de la red y, por lo tanto, la relación entre distintos precios. Este cambio en las relaciones puede ser visto como un cambio en la estructura de precios relativos de la economía, por lo que puede concluirse que durante la crisis de 2002 se produjo un proceso de inflación alta acompañada de cambios fuertes en los precios relativos.

Los resultados anteriores permiten concluir que la estructura de precios de la economía uruguaya es sumamente volátil, e incluso es probable que no exista una estructura subyacente. Si bien el trabajo parte de la base de que la inflación puede ser vista como el resultado emergente de un sistema complejo, a lo largo del trabajo se recolectaron pruebas suficientes para asegurar que esto es plausible. Si aceptamos esta premisa, parece razonable pensar que es muy difícil realizar predicciones de la inflación, al menos en el largo plazo. Esto parece ser coherente con los errores que cometen sistemáticamente quienes usan modelos de predicción lineales, que pueden funcionar relativamente bien en el corto periodo, pero no en el largo plazo. La evidencia empírica (^{Curtin, 2009}; Coibiony Gorodnichenko, 2015; ^{Frachey Lluberas, 2019}; ^{Chen, 2019}) muestra que los valores esperados por los consumidores se ajustan mejor a la realidad que los valores esperados por los expertos, pese a su estatus de conocedores del modelo subyacente de la economía.

Como se pudo comprobar, la dinámica, evolutividad y falta de una estructura fija subyacente son características presentes en el periodo de estudio, y estas, a su vez, son parte de lo que define a un sistema complejo. Asimismo, los cambios en la estructura de precios relativos hacen que sea difícil obtener una buena estimación de la inflación y más aún su predicción. Esto puede generar problemas importantes en los ajustes económicos y planificación de políticas que se realizan tomando como uno de los indicadores importantes los niveles de inflación. Tal es el caso de laya mencionada "cláusula gatillo" del caso uruguayo, o las proyecciones que los diferentes actores económicos (bancos centrales, empresas y consumidores) consolidan para maximizar su beneficio. Como ya se ha señalado, en cualquier caso las dinámicas inflacionarias y de la red de precios subyacente son muy diferentes en el caso de inflaciones (relativamente) bajas que altas. Estos resultados plantean limitaciones acerca de la plausibilidad de efectuar proyecciones sobre la inflación a plazos largos.

Los resultados de este trabajo y los desarrollos acerca de los cambios en los indicadores del sistema ante el advenimiento de un periodo de inestabilidad hacen que sea plausible utilizar estos indicadores como señales de alerta para anticipar problemas inflacionarios en un futuro. Sin embargo, es preciso remarcar algunas limitaciones del trabajo. El cambio de base en la mitad del periodo provoca que los datos no sean estrictamente comparables (al igual que tampoco son las redes que se construyen a partir de estos).

Otra limitante es la utilización de la correlación lineal para la construcción de enlaces, dado que esta no permite captar relaciones no lineales entre las dinámicas de precios. Futuras investigaciones podrían incluir la verificación de la plausibilidad de utilizar relaciones lineales entre los precios, lo que podría ser diferente dependiendo los niveles de inflación. Asimismo, para futuros trabajos se podría emplear otra métrica para construir los enlaces que hagan posible captar otro tipo de relación por fuera de la lineal. A su vez, se podría estudiar la sensibilidad de los resultados ante cambios en el valor delumbral usado para filtrarlas correlaciones (u).