SISTEMA DE VISIÓN SINÉRGICO PARA DETECCIÓN DE MOVIMIENTO

SYNERGIC VISION SYSTEM FOR MOTION DETECTION

 

MA. TERESA GARCÍA RAMÍREZ
Universidad Autónoma de Querétaro-Instituto Politécnico Nacional,CICATA-Qro, Centro Universitario, Col. Las Campanas, Querétaro, Qro. México, teregar@uaq.mx

HUGO JIMÉNEZ HERNÁNDEZ
Instituto Politécnico Nacional, CICATA-Qro, Colinas del Cimatario, Querétaro, Qro. México

JOAQUÍN SALAS RODRÍGUEZ
Instituto Politécnico Nacional, CICATA-Qro, Colinas del Cimatario, Querétaro, Qro. México

JOSÉ-JOEL GONZÁLEZ- BARBOSA
Instituto Politécnico Nacional, CICATA-Qro, Colinas del Cimatario, Querétaro, Qro. México

 

Recibido para revisar Agosto 5 de 2009, aceptado Marzo 2 de 2010, versión final Mayo 20 de 2010

 

---

RESUMEN: La detección de movimiento en sistemas de vigilancia y monitoreo se ve favorecida por la combinación sinérgica de diferentes tipos de cámaras y su óptima distribución sobre el área de interés. Se propone un modelo de optimización para un sistema de visión sinérgico basado en programación lineal entera. Los objetivos son encontrar la posición y orientación óptima de cada una de las cámaras direccionales y omnidireccionales con el fin de maximizar la cobertura del espacio de trabajo y detectar los objetos en movimiento presentes. Para detectar eficientemente el movimiento, incluso ante cambios de luminosidad globales, se utiliza un algoritmo de substracción de fondo que usa la información espacial de la textura. El método propuesto se evalúa en un conjunto representativo de escenarios reales utilizando una red de cámaras. Los resultados muestran que nuestro algoritmo es capaz de determinar el número mínimo de cámaras necesario para cubrir un área determinada.

PALABRAS CLAVE: Visión sinérgica, optimización, detección de movimiento, cámara omnidireccional, cámara direccional.

ABSTRACT: Motion detection in surveillance and monitoring systems is enhanced by the synergistic combination of different kinds of cameras and their optimal distribution over the area of interest. We developed an optimization model for a synergistic vision system based on integer lineal programming. The objectives consist in the following: on one hand computing the optimal position and orientation of all directional and omnidirectional cameras, in order to maximize the workspace coverage and on the other hand detecting the objects motion in the workspace. To detect efficiently the movement, even under global luminosity changes, is used a background subtraction algorithm, which uses spatial information of texture. The proposed method is evaluated using a representative set of real sceneries and a network of cameras. Outcomes show that our algorithm is able to determine also the minimal cameras network configuration required to cover a given area.

KEY WORDS: Synergistic vision, optimization, motion detection, omnidirectional camera, directional camera.

---

 

1. INTRODUCCIÓN

Los sistemas para monitoreo y vigilancia requieren de un conjunto de cámaras para cubrir grandes áreas de trabajo. Sin embargo, el procesamiento computacional de imágenes de los sistemas es proporcional al número de cámaras. Con el objetivo de reducir la carga computacional del sistema de monitoreo es necesario utilizar una combinación de diferentes tipos de cámaras para detectar eventos que involucran la interacción de personas, equipos, u otros objetos de manera efectiva. El tipo de cámara omnidireccional tiene como ventaja la capacidad de adquirir 360^o del ambiente de trabajo en una sola imagen, sin embargo la resolución de las imágenes es pobre. Por otro lado, las cámaras direccionales tienen como ventaja una alta resolución de las imágenes, sin embargo el ángulo de visión es reducido. El sistema sinérgico para la detección de movimiento propuesto en este artículo consta de un arreglo de cámaras omnidireccionales y direccionales. La combinación sinérgica propuesta permite monitorear grandes áreas utilizando las capacidades de las cámaras omnidireccionales del tipo catadióptrico sin necesidad de sacrificar la resolución con la que los objetos en movimiento son capturados. En este artículo, la posición y orientación de las cámaras direccionales y omnidireccionales es calculado de manera óptima.

Para analizar e inferir la actividad realizada por una persona u objeto en movimiento, usualmente, se emplean modelos de substracción de fondo, donde algunos de los trabajos más significativos son los de Stauffer y Grimson [1] donde su propuesta consiste en modelar el pixel como una variable aleatoria con una distribución normal. Toyama et al. [2] proponen un modelo capaz de descartar movimiento periódico del fondo como en el caso de olas de mar o de movimiento de escaleras eléctricas. Elgammal et al. [3] proponen modelar la intensidad anterior inmediata del pixel y Horprasert et al. [4] proponen un método de substracción del fondo que utiliza el método del residuo. Por otro lado, Wettergren y Costa proponen métodos heurísticos para detección de objetos en movimiento en una red de sensores para vigilancia [5].

Para que la detección de objetos en movimiento sea efectiva, se requiere de la posición y orientación óptima de cada una de las cámaras del sistema sinérgico de tal forma que se logre maximizar la cobertura de un espacio de trabajo, representado por una rejilla o grid de ocupación [6]. Así, las primeras publicaciones relacionadas con la colocación óptima surgieron a mediados del siglo XIX [7], y estuvieron en relación con la ubicación de lámparas y guardias. En los últimos años, el estudio de colocación óptima de dispositivos considera redes de cámaras, redes de transmisión (teléfono, LAN, WAN, Wireless) y sistemas de posicionamiento geográfico (GPS). Diversos trabajos sobre redes de sensores, como los de Wang, Chakrabarty, Höster, Meguerdichian y Murray, han propuesto algunas soluciones para el problema de colocación de sensores [8-12]. Así mismo, se han propuesto soluciones óptimas al Problema de la Galería de Arte (PGA) y sus variantes [7], para la colocación de "guardias" en un área poligonal, donde la tarea consiste en calcular un número mínimo de guardias y sus posiciones estáticas, de manera que todos los puntos de un polígono sean observados. En otro sentido, Jordan y Roy consideran el problema de colocación de sensores para localizar de manera óptima un agente, para ello utilizan el error de posición para determinar la exactitud de localización del agente [13]. En este documento, se presenta el estudio del problema de colocación óptima de cámaras direccionales y omnidireccionales en un sistema de visión sinérgico, para detectar el movimiento de objetos a través de las cámaras omnidireccionales y la posición y visualización del objeto a través de las cámaras direccionales.

El resto del documento está organizado de la siguiente manera, en la sección 2, se presenta la solución propuesta para la colocación de las cámaras del sistema de visión sinérgico, describiendo los modelos de proyección de las cámaras y el espacio de trabajo. En la sección 3, se describen los algoritmos para detección de movimiento aplicado a las imágenes omnidireccionales. En esta misma sección se presenta como un objeto en movimiento es proyectado a una posición en un mapa 2D del ambiente de trabajo. En la sección 4, se muestran los resultados del algoritmo aplicado a diferentes escenarios. Por último, en la sección 5, se concluye resumiendo la importancia de utilizar un sistema de visión sinérgico, seguido por una lista de referencias.

 

2. SISTEMA DE VISIÓN SINÉRGICO

Para lograr la detección de movimiento a través de un sistema de visión sinérgico óptimo, se describe el modelo de proyección de las cámaras direccionales y omnidireccionales, el espacio de trabajo y el modelo de optimización que resuelve el problema.

2.1. Modelo de proyección de las cámaras
En este trabajo, se asume el modelo de proyección de la cámara CCD del tipo pinhole, de tal forma que el mapeo de un punto del mundo real a un punto en el plano imagen (u,v), se realiza a través de las siguientes ecuaciones:

Donde x_c, y_c y z_c definen el punto 3D, f es la distancia focal y (u₀,v₀) son las coordenadas del punto principal.

El modelo de proyección del sistema catadióptrico, con espejo parabólico y lente telecéntrica, que permite la relación entre un punto 3D del mundo real (x_c, y_c, z_c) y un punto en el plano imagen (u,v), está definido por las ecuaciones:

Donde h es el parámetro de curvatura del espejo, a_x y a_y son los parámetros intrínsecos de la cámara.

En la Figura 1, se muestra el modelo de proyección de las cámaras direccionales y catadióptricas, que se define como el campo de visión proyectado sobre la superficie del terreno.

Figura 1. Campos de visibilidad de las cámaras proyectados en la superficie del terreno
Figure 1. Fields of view of cameras projected on the ground

2.2. Modelo de visibilidad de las cámaras
La visibilidad de una cámara está determinada por el campo de visión, la profundidad de campo y la curvatura del espejo. Así, para determinar si una celda en la rejilla está en el campo de visión de la cámara direccional, la posición x = (x, y) de la celda en la rejilla se rota y se traslada con respecto a las coordenadas de la cámara x′ = (x′, y′) esto se muestra en (3).

Mientras que para las cámaras catadióptricas la celda z = (x, y) únicamente se traslada con respecto a las coordenadas de la cámara z′ = (x′, y′) , esta transformación se define como:

Posteriormente se verifica si el punto transformado está dentro del campo de visibilidad de la cámara direccional, aplicando las restricciones mostradas en (5), donde d es la distancia de la cámara al objeto en la escena y a es el ancho de escena.

Así mismo, para la cámara catadióptrica se verifica si la distancia euclidiana d_e entre la posición z′ de la cámara y el punto transformado z es menor o igual al radio r_e de visibilidad de la cámara, esto es:

2.3. Modelo del Espacio de Trabajo
Consideramos cuatro componentes en el modelo del espacio de trabajo: el diseño del espacio de trabajo, los obstáculos, las oclusiones y la frecuencia de muestreo (f_s). El primer componente define el área que necesita ser cubierta con un mínimo número de cámaras, definido como W_s = S - M_c, donde S = {x=(x, y) | x Î (Z⁺)², 1 £ x £ m; 1 £ y £ n} y M_c Ì S. El segundo componente corresponde a los obstáculos, que son áreas en el espacio de trabajo que obstruyen la visibilidad y colocación de las cámaras, dado por M_ob = {x=(x, y) | x Î (Z⁺)²; x Î W_s }. El componente oclusiones representa el área que no puede ser vista por una cámara, en una posición y orientación específica, debido a la presencia de obstáculos en el medio ambiente (ver Figura 2).

Figura 2. Oclusión generada por el objeto en (4,4)
Figure 2. Occlusion produced by the object in (4,4)

Para determinar si un punto pen la posición i (p_i) está ocluido para una cámara ubicada en la posición x₀, se define el vector f de la posición de la cámara x₀ al punto p_i y el vector g de x₀ al obstáculo M_ob en la posición j. Posteriormente se verifica que la distancia al punto p_i proyectado en dirección al obstáculo sea mayor que ║g║ . Y que el ángulo formado entre los vectores f y g sea menor al umbral z definido por p/ang donde ang está relacionado con el área mínima de oclusión permitida para una celda de la rejilla sin que sea considerada como ocluida totalmente. Entonces, el mapa de oclusiones M_oc se define como:

Finalmente, la frecuencia de muestreo permite definir la distancia entre las celdas de la rejilla, logrando ubicaciones más precisas de las cámaras u objetos, ya que entre mayor sea la frecuencia de muestreo, la distancia entre las celdas de la rejilla se reduce dando como resultado una resolución mayor (ver Figura 6). En la Figura 3, se muestra el espacio de trabajo utilizado para el sistema de visión sinérgico, el cual incluye obstáculos producidos por los módulos de trabajo en forma de cruz con altura de 1.7 m y una frecuencia de muestreo f_s=1.0.

Figura 3. Espacio de trabajo. Las áreas grises son módulos de trabajo que se convierten en obstáculos.
Figure 3. The workspace. The gray areas are office furniture that become obstacles.

2.4. Solución del sistema de visión sinérgico
Una vez definidos los mapas de visibilidad para cada posición y orientación de las cámaras. El problema de optimización se resuelve por sus características con Programación Lineal Entera [14], formulándose como: dado un conjunto de celdas de la rejilla y dos tipos de sensores visuales con diferentes parámetros en los campos de visibilidad, encontrar el mínimo número de cámaras que garantice la cobertura de un espacio de trabajo. Esto es:

Donde {i=(x₁, y₁) | i Î W_s}. Las variables c_ib y p_i se definen como:

Las restricciones del problema están dadas por los modelos de cámaras y el espacio de trabajo. En esta sección se considera que el espacio de trabajo es cubierto por cámaras direccionales y omnidireccionales simultáneamente, logrando así un sistema sinérgico. La ecuación (11) representa el área cubierta por cámaras direccionales y omnidireccionales.

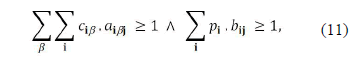
donde {i=(x₁, y₁) | i Î W_s}, {j=(x₂, y₂) | j Î W_s}. Las variables b_ij y a_ibj se definen en (12) y (13).

Para asegurar que en cada celda solo exista un tipo de cámara, es necesario añadir la siguiente restricción:

En la práctica el algoritmo puede dar como resultado fracciones de cámaras a colocar en el espacio de trabajo (ver Tabla 1), esto es que el número de posiciones obtenido es mayor que el número de cámaras óptimo (n_c), en estos casos es necesario realizar el proceso de optimización nuevamente [15], considerando únicamente las posiciones encontradas en el proceso previo, asignándoles un uno y agregando la restricción que el número de cámaras disponibles es inferior o igual a (n_c). La ecuación (15) muestra las restricciones para obtener las posiciones óptimas para un número de cámaras direccionales u omnidireccionales disponible.

donde {i=(x₁, y₁) | i Î W_s}, {j=(x₂, y₂) | j Î W_s}. Una vez definido el modelo de optimización para resolver el problema de cobertura del espacio de trabajo, se plantea el problema de detección de movimiento mediante el uso de una mezcla de cámaras direccionales y omnidireccionales.

 

3. DETECCIÓN DE MOVIMIENTO

La detección de movimiento se efectúa mediante un modelo de substracción de fondo basado en la modificación [1]. La propuesta considera la razón de cambio espacial de las intensidades de un píxel con un vecindario predeterminado. Al considerar la razón de cambio espacial, este modelo resulta útil para ambientes con gran cantidad de información en textura y con cambios de luminosidad globales.

Dada una imagen adquirida en un tiempo t (I_t), se calcula para cada una de las posiciones x_i de la imagen I_t la razón de cambio con respecto a un vecindario predeterminado y representado por V={x_j¹,x_j²,… x_j^N}. La intensidad de la imagen I_t en la posición x_i está dada por I_t (x_i), por lo que la razón de cambio con respecto al vecindario predeterminado está definido como:

W(I_t) indican las variaciones de la intensidad del vecindario. Estas relaciones se mantienen cuando no existan cambios en el píxel de referencia x_i y su vecindario correspondiente. Si las relaciones del píxel de referencia x_i con respecto a su vecindario cambian, es muy probable que el píxel o parte del vecindario esté ocluido. Las relaciones entre el píxel de referencia y cada pixel del vecindario se modelan como una variable aleatoria con una distribución normal I_t ((x_i)-I_t (x_i+d_j)) ≈ G_t (m_t(x_i) ,s _t (x_i)), tal que m _t (x_i) y s _t (x_i) son los parámetros de la Gaussiana.

Donde N corresponde al número de elementos de V.

Figura 4. Cálculo de la razón de cambio espacial de las intensidades de un píxel en la posición x_i con respecto a sus vecinos V = {x_j¹,x_j²,…}. Los píxeles vecinos son predeterminados y pueden definirse a cualquier distancia y cualquier dirección
Figure 4. Computing the intensity spatial change rate of a pixel in x_i position with respect to neighbors V = {x_j¹,x_j²,…}. The neighboring pixel are predetermined and can be defined at any distance and any direction

Los parámetros de las Gaussianas son considerados como un problema de datos incompletos, de manera que estos parámetros pueden ser estimados iterativamente mediante el algoritmo de Máxima Verosimilitud [14]. La presencia de movimiento en una posición x_i de la imagen está determinada si mantiene las relaciones previamente modeladas por su vecindario V. Esto es, para el punto x_i y el punto del vecindario x_j Î V no pertenece al modelo si .

Se asume que la observación corresponde al fondo con una perturbación. Típicamente el valor asignado a a es de 3, lo que significa que el 99.73% de los casos W(I_t(x_i)) está en este modelo. Los parámetros de la Gaussiana se adaptan con respecto al tiempo mediante la maximización de la expectativa [1], tal que

Donde 0≤ r ≤ 1 es una razón de aprendizaje.

3.1. Proyección del objeto en movimiento al mundo real
A partir de la detección de movimiento en las imágenes omnidireccionales, se determina la cámara direccional que tiene mejor visión del objeto, para esto se debe conocer la posición en el mundo real del objeto en movimiento. La ecuación (2) expresa las relaciones entre un punto 3D y un punto 2D en la imagen, tal que despejando z_c de u = f(x_c, y_c, z_c, a_x, h, u₀) y sustituyéndola en v = f(x_c, y_c, z_c, a_y, h, v₀), tenemos que:

Si consideramos que el objeto es perpendicular al piso y lo suficientemente delgado para que quede dentro de una celda de la rejilla del espacio de trabajo, x_c y y_c pueden considerarse constantes. Bajo estas restricciones podemos deducir que la ecuación anterior representa una línea recta que pasa por el centro de la imagen (ver Figura 5(a)).

Figura 5. El movimiento de una persona o de un objeto que es perpendicular al piso puede modelarse como la línea radial de mayor tamaño
Figure 5. The movement of a person or an object which is perpendicular to the floor can be modeled as the radial line largest

Por lo anterior, nuestra búsqueda del objeto se centra en el segmento radial de mayor longitud en la imagen sin fondo. Si súmanos los valores de la imagen sin fondo a lo largo de cada línea radial, la línea radial de mayor tamaño tendrá el menor valor de la suma. Para hacer esta suma se usan técnicas de tablas de consulta (lookup table), las cuales son precalculadas. La figura 5 (b) muestra la suma de los valores de la imagen sin fondo (figura 5(a)) a lo largo de cada línea radial. El valor mínimo de la Figura 5(b) en q = 94.26º indica el segmento radial de mayor longitud del objeto en movimiento. La posición del objeto en el suelo (u_x,v_x) corresponde al punto más cercano al centro de la imagen (r) en la dirección de 94.26º. Donde u_x =rcos(q) y v_x = rsin(q). Usando (2), deducimos que la posición del objeto en el mapa 2D está dado por:

donde H corresponde a la altura de la cámara catadióptrica respecto al suelo, , y .

Estas ecuaciones proyectan el objeto en movimiento a una posición en el mapa 2D que caracteriza el ambiente de trabajo. A partir de la posición 2D del objeto en movimiento se determina cual de las cámaras direccionales posee una mejor visión.

 

4. RESULTADOS

En esta sección se muestran los resultados experimentales de los algoritmos de colocación de las cámaras direccionales y catadióptricas de manera particular, para posteriormente mostrar los resultados de la mezcla de cámaras que permite la implementación del sistema de visión sinérgico. El espacio de trabajo se basa en una rejilla o mapa de ocupación. Los resultados se muestran en espacios de trabajo con y sin obstáculos. Para el modelo de visibilidad de la cámara, se consideró la oclusión de las celdas de la rejilla provocada por los obstáculos. Además, cada celda de la rejilla representa un metro en el entorno real, esto es fs=1.0. La solución fue programada en Microsoft Visual C++ versión 6.0. Para el proceso de optimización, se utilizó lpsolve versión 5.5.0.10 de acceso libre, que puede resolver problemas de programación lineal entera, basado en el método Simplex y el algoritmo de ramificación y poda [17].

El problema de optimización se resolvió utilizando un solo tipo de cámaras direccionales con formato del CCD de 1/3². Y para las cámaras omnidireccionales, se utilizó el mismo tipo de cámara direccional con un espejo parabólico de diámetro 8 cm y radio de curvatura de 3.5 cm.

La detección de movimiento se realizó en las imágenes obtenidas de las cámaras omnidireccionales, posteriormente se realizó una trasformación de coordenadas 2D (sección 3.1), para obtener la posición del objeto y con ello determinar las cámaras direccionales que cubrían al objeto en movimiento en un tiempo t.

4.1. Cámaras direccionales
En esta sección se muestran dos ejemplos de espacios de trabajo, considerando el uso de cámaras direccionales únicamente. Además se restringió la orientación de las cámaras a un cierto número de grados de libertad. Para los espacios de trabajo mostrados en la Figura 6, se consideraron dos grados de libertad en la orientación de las cámaras, partiendo de un ángulo inicial b = 90º y un incremento en el ángulo de 180º. La Figura 6 muestra los resultados para un espacio de trabajo de (3 × 6) metros y variación en la frecuencia de muestreo. La Figura 6(a) muestra el resultado para una f_s=1.0 y en la Figura 6(b) es el resultado para una f_s=2.0 donde el número de cámaras en ambos casos sigue siendo la misma ya que el área de trabajo no se modifica solo la distancia entre las celdas de la rejilla.

Figura 6. Posiciones y orientaciones óptimas de las cámaras direccionales con una f_s específica
Figure 6. Optimal positions and orientations of the directional cameras with a specific f_s

Cuando el espacio de trabajo tiene obstáculos, es necesario tener en cuenta las oclusiones generadas por el medio ambiente y los objetos. Para los espacios de trabajo de la Figura 7, se consideraron cuatro grados de libertad en la orientación de las cámaras, partiendo de un ángulo inicial b = 0º, un incremento en el ángulo de 90º y una f_s = 1.0.

Figura 7. Cobertura del espacio de trabajo para n_c=7. Observando una celda sin cubrir al 100% esto debido a que n_c se aproximó al entero inmediato inferior
Figure 7. The coverage of workspace for n_c=7. We observe a cell without 100% cover, because n_c was closed to next lower integer

Los resultados obtenidos se muestran en la Tabla 1, e indican las posiciones de las cámaras para cada orientación. El número óptimo de cámaras es n_c = 7.1, el cual no es un entero, por lo tanto este valor se aproxima al número entero inmediato superior o inferior, ya que no existen fracciones de cámara.

Tabla 1. Posiciones de cada porción de cámara, representada por los números y una subtabla para la respectiva orientación
Table 1. Positions of each portion of camera represented by numbers, and one subtable for each orientation

En la Tabla 1, se observa que los resultados obtenidos son fracciones de cámara a colocar en celdas del espacio de trabajo. Por lo tanto, se realiza nuevamente el proceso de optimización restringiendo las posiciones y el número de cámaras disponible al resultado previo (Tabla 1 y n_c = 7). En la Figura 7, se muestra el resultado obtenido después de repetir el proceso de optimización.

4.2. Cámaras omnidireccionales
En este apartado, se muestra un ejemplo de un espacio de trabajo considerando el uso de cámaras omnidireccionales únicamente. Para los cuales, se ha considerado que el radio interno es aproximadamente igual a cero, por lo tanto, sólo se utiliza el radio exterior r = 3m, que limita el rango de visibilidad de las cámaras y una frecuencia de muestreo f_s = 1.0. Para el espacio de trabajo representado en la Figura 8, se obtienen las posiciones de las cámaras que se muestran en la Tabla 2, el número óptimo de las cámaras es n_c=5.16, este valor resulta de las sumas de las fracciones de las cámaras presentado en la tabla 2.

Tabla 2. Posiciones de las cámaras omnidireccionales para el espacio de trabajo de la Figura 8, con radio r = 3.
Table 2. Positions of the omnidirectional cameras to the workspace in Figure 8, with radius r=3.

Figura 8. Se observa la cobertura total del espacio de trabajo con obstáculos
Figure 8. Shows the total coverage of the workspace with obstacles

Como se puede observar existen fracciones de cámara a colocar en el espacio de trabajo, por lo tanto es necesario realizar el proceso de optimización nuevamente, restringiendo el número de cámaras y las posiciones de las mismas, obteniéndose como resultado las posiciones mostradas en la Figura 8.

4.3. Sistema de visión sinérgico
Para el espacio de trabajo de la Figura 3, se consideraron cuatro grados de libertad en la orientación de las cámaras direccionales, partiendo de un ángulo inicial b = 0º e incremento en el ángulo de 90º. Y dos cámaras catadióptricas con radio r = 9m y f_s = 1.0. En la Figura 9, se muestra el arreglo de cámaras para el sistema de detección de movimiento a través de un sistema de visión sinérgico. Se observa que el espacio de trabajo es cubierto completamente por las cámaras direccionales y omnidireccionales. Para poder adquirir una mayor porción de las personas u objetos en movimiento, las cámaras direccionales fueron colocadas a 1.80m de altura. Mientras que las cámaras omnidireccionales se ubicaron a la altura del plafón (aproximadamente 3.5m) reduciéndose de esta manera las oclusiones generadas por los obstáculos.

Figura 9. Ubicación de cámaras direccionales ( 1 a 12) y omnidireccionales (señaladas con circulo) en un espacio de trabajo real con área 8 ´ 25 m²
Figure 9. Location of directional cameras (1 to 12) and omnidirectional (show as circule) cameras in a real workspace with an area 8 ´ 25 m²

4.4. Detección de movimiento
En la Figura 10, se muestran algunas imágenes donde se ha detectado movimiento en la cámara omnidireccional (ver Figura 11). Se observa en la Figura 10, que los contornos son detectados eficientemente, ya que el modelo utiliza la información del comportamiento de la textura.

Figura 10. Segmentación del fondo en una secuencia de imágenes de una cámara omnidireccional
Figure 10. Background segmentation in a sequence of images from an omnidirectional camera

Figura 11. Detección de movimiento de una persona en la imagen omnidireccional del espacio de trabajo mostrado en la Figura 3
Figure 11. Motion detection of a person in the omnidirectional image in the workspace shown in Figure 3

Una vez detectado el objeto u objetos en movimiento se proyecta la imagen omnidireccional a 2D, y a partir de ésta se buscan las cámaras direccionales que visualizan el objeto. Señalando el porcentaje observado del objeto por cada cámara. En la imagen de la Figura 12, se muestra el resultado de las cámaras direccionales que cubren o visualizan los objetos en movimiento detectados por la cámara omnidireccional (Figura 11) en un tiempo t.

Figura 12. Ubicación de la persona detectada en la Figura 11en un tiempo t, observada por 2 cámaras direccionales. La cámara 8 visualiza sólo un 50%, mientras que la cámara 5 observa el 100% de la persona
Figure 12. Location of the person detected in Figure 11 at time t, who is observed by 2 directional cameras. The camera 8 sees only 50%, while the camera 5 sees 100% of the person

 

5. CONCLUSIÓN

En este trabajo se ha formulado el problema de optimización para la colocación de un arreglo de cámaras direccionales y omnidireccionales para un sistema de visión sinérgico. El modelo planteado está basado en programación lineal entera y un mecanismo de optimización de una o más fases. Además, este modelo considera el manejo de oclusiones causadas por objetos dentro del espacio de trabajo. Debido a la naturaleza del modelo, la inclusión de las rejillas de ocupación permitió representar los espacios de trabajo en diferentes niveles de resolución de acuerdo al valor de la frecuencia de muestreo. Además estas rejillas permitieron describir de manera precisa los mapas de visibilidad de cada cámara. Con los resultados experimentales se verificó que el algoritmo es capaz de obtener el número óptimo de cámaras en diferentes escenarios. Sin embargo, en algunos casos, por las restricciones del escenario, la solución obtenida no es precisa y se requiere aplicar más de una fase del proceso de optimización con nuevas restricciones. Así mismo, el algoritmo propuesto para la detección de movimiento, es eficiente debido a que obtiene imágenes con poco ruido cuando se aplica a imágenes omnidireccionales. Finalmente, el uso de un sistema de visión sinérgico ha permitido la detección de movimiento de manera eficiente.

 

AGRADECIMIENTOS

Los autores agradecen el apoyo proporcionado por el Centro de Investigación en Ciencia Aplicada y Tecnología Avanzada del Instituto Politécnico Nacional unidad Querétaro, así como a la Universidad Autónoma de Querétaro, que permitieron llevar a cabo el desarrollo de este proyecto de investigación. Además este trabajo fue financiado por los proyectos SIP:20091721 y SIP:20091654, así como CONACYT: CB-2005-01-51004 y CB-2005-01-51005. Y la beca de estudios de posgrado otorgada por la Universidad Autónoma de Querétaro.

 

REFERENCIAS

[1] STAUFFER C. y GRIMSON W. "Adaptive Background Mixture Models for Real-Time Tracking.," IEEE Conference on Computer Vision and Pattern Recognition., pp. 2:252-259, 1999.         [ Links ]
[2] TOYAMA B. , KRUMM K., BRUMITT J. y MEYERS, B. "Principles and Practice of Background Maintenance.," ICCV, pp. 312-330, 1999.         [ Links ]
[3] ELGAMMAL A., HARWOOD D. y DAVIS L.S. "Non-Parametric Model for Background Substration.," Proceedings of the 6th European Conference on Computer Vision-Part II, pp. 751- 767, 2000.         [ Links ]
[4] HORPRASERT T., HARWOOD, D. y DAVIS L.S. "A Robust Background Substration and Shadow Detection," Proceedings on Asian Conference on Computer Vision, 2000.         [ Links ]
[5] WETTERGREN T. Y COSTA R. "Optimal Placement of Distributed Sensors Against Moving Targets". ACM Transactions on Sensor Networks, Vol. 5, No. 3, pp. 26:1 - 25, 2009.         [ Links ]
[6] ELFES A., "Using Occupancy Grids for Mobile Robot Perception and Navigation," Computer, Vol. 22, pp. 46 - 57, 1989.         [ Links ]
[7] URRUTIA J., "Art Gallery and Illumination Problems," in Handbook on Computational Geometry. North-Holland: Jorge Rudiger Sack and Jorge Urrutia, Elsevier Science, pp. 973-1027, 2000.         [ Links ]
[8] WANG J. y ZHONG N. "Efficient Point Coverage in Wireless Sensor Networks," Kluwer Academic Publishers, pp. 1-15, 2006.         [ Links ]
[9] CHAKRABARTY K., IYENGAR S., HAIRONG Q. y EUNGCHUN C. "Grid Coverage for Surveillance and Target Location in Distributed Sensor Networks," Computers IEEE Transactions, pp. Vol. 51, 1448-1453., 2002.         [ Links ]
[10] HÖSTER E. y LIENHART R. "Approximating Optimal Visual Sensor Placement," Multimedia and Expo, IEEE International Conference, pp. 1257-1260, 2006.         [ Links ]
[11] MEGUERDICHIAN S., KOUSHANFAR F., POTKONJAK M., y SRIVASTAVA M. "Coverage Problems in Wireless Ad-hoc Sensor Networks," Twentieth Annual Joint Conference of the IEEE Computer and Communications Societies. Proceedings. IEEE, pp. 1380-1387, 2001.         [ Links ]
[12] MURRAY A., KIM K., DAVIS J., MACHIRAJU R. y PARENT R. "Coverage Optimization to Support Security Monitoring," Computers, Environment and Urban Systems, Vol. 31(2), pp. 133-147, 2007.
[13] JOURDAN D. y ROY N. "Optimal sensor placement for agent localization". ACM Transactions on Sensor Networks, Vol 4(3), pp. 1-40, 2008.         [ Links ]
[14] LIENHART R. y HÖSTER E., "On the Optimal Placement of Multiple Visual Sensors," Augsburgo Germany , Technical Report 2006.         [ Links ]
[15] LIN S. y KERNIGHAN B. W. "An Effective Heuristic Algorithm for the Traveling-Salesman Problem," Operations Research, Vol. 21(2) pp. 498-516, 1973.         [ Links ]
[16] DEMPSTER A., LAIRD N. y RUBIN D. "Maximum Likelihood from Incomplete Data via the EM Algorithm.," Journal of the Royal Statistical Society, Vol. 39(1), pp. 1-38, 1977.         [ Links ]
[17] BERKELAAR M. (2008, August) lp_solve reference guide. [Online]. "http://lpsolve.sourceforge.net/5.5/".         [ Links ]