1. Introduction
Population growth in coastal areas due to multiple human activities, such as recreation, industrial expansion, and economic exploitation, exposes coastal inhabitants to the permanent threat of erosion, flooding, and natural disasters [1]. These events might be triggered by a significant rise in sea level due to strong winds (tropical storms), cold fronts and lower atmospheric pressure [2-4]. These latter phenomena have been grouped into and named as meteorological tides (MT) [5], whereas the regular oscillations of the sea level induced by the gravitational forces of the Earth-Moon-Sun system are denominated astronomical tides (AT) [6]. The sea level at a certain moment is calculated by adding the (AT) to the (MT) [6]. The sum of these components constitutes a crucial parameter for calculating the levels of hazard linked to coastal areas flooding, as well as in the estimation of wave crest heights for safety in port and maritime projects. Some studies have been carried out in the Caribbean Sea to estimate the trend and variability of sea level fluctuations, using tide-gauge historical records and satellite altimetry [7]. However, several locations along the Caribbean littoral lack reliable data or their spatial/temporal resolution is inadequate for such analysis; thus, difficulting the assessment of sea level rise triggered by extreme climatological events as well as the implementation of measures for coastal flood prevention and mitigation.
There have not been any studies focusing on determine the sea levels accurately and on a long-term perspective in the Colombian Caribbean. Particularly, in areas with scarce and disperse tide-gauge records. Most studies focused on assessing the partial contribution to sea level coming from both tide components. Some authors have estimated the height of flooding in coastal areas considering sea level as an important component within the flood systems [8-10].
These latter authors respectively used the same methods for the regions of the Pacific and Caribbean coasts in Colombia, using instrumental series and analyzing the astronomical and meteorological tides separately. The latter component was analyzed from residual meteorological data, the series that remains after deducting the level of the astronomical tide from the original instrumental series. These studies used the hypothesis that the residual meteorological data corresponds to variations in sea level due mostly to wind and atmospheric pressure.
Furthermore, these studies assumed that each instrumental sea level series is representative for a region within each area studied, which means that the methods do not consider whether the coastal area is an open area or is a semi-enclosed body of water, such as bays, gulfs, estuaries or mouths. Other studies identified and analyzed oceanographic parameters in the Mira River delta and the Bay of Tumaco on the Colombian Pacific coast [11,12]. These investigations used a long-wave numerical model to reconstruct series of astronomical tides, as well as the residual instrumental meteorological series from Tumaco to represent the behavior of the meteorological tide due to pressure and wind. Globally, other authors take into account sea levels to determine flood levels caused by the combination of oceanographic effects [13-17].
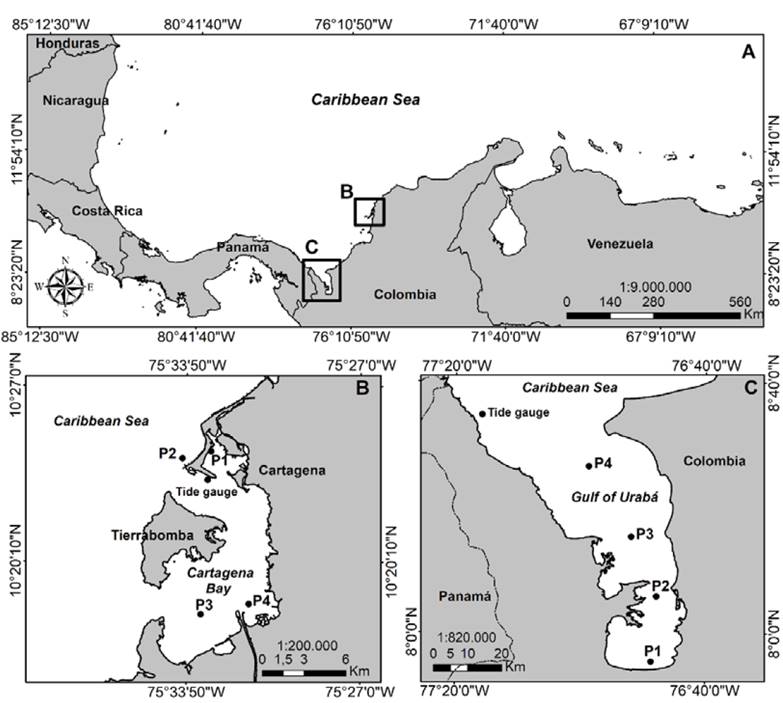
This work aims to present an alternative method for the construction of sea levels regimes in microtidal areas with low spatial coverage of tide gauges for measuring sea level, a lack of extensive time series, or non-existent data, from the numerical reconstruction of the sea level, considering the contribution of astronomical and meteorological components at the same time, as well as local effects of variations in the bottom and contours. The validation and verification of this method was performed in two areas of the Colombian Caribbean Coast: The Bay of Cartagena and the Gulf of Urabá (Fig. 1).
Source: The authors
Figure 1 A. Location of Cartagena Bay and the Gulf of Urabá in the Colombian Caribbean. B. Computational domain for Cartagena Bay. C. Computational domain for the Gulf of Urabá. In A and C, the tide gauge points indicates the place where the measured data in the field were obtained for model calibration. The other points (P1, P2, P3, P4) indicate the places where the sea level simulations were performed with a temporary extension of 20 years for the study areas.
Phenomena such as tsunamis, fluvial discharge of large rivers, and other anomalies generated by ocean-atmospheric phenomena or climatic effects such as the melting of the poles, which determine the flooding of low-lying coastal areas, were not considered in the methods proposed hereafter.
In its first stage, the method is based on the application of a hydrodynamic model comprising the equations of long waves to simultaneously model the astronomical and meteorological tides. The numerical results are calibrated using instrumental records (tide-gauges) from two areas of Colombia’s Caribbean region, the Bay of Cartagena and the Gulf of Urabá (Fig. 1A, 1B). Once the results were validated, the numerical model was able to generate the series of data used for the construction of the mean and extreme sea level regimes
2. Methods
The first step for implementing this methodology was to set the initial conditions of the hydrodynamic model H2D [18]. A computational mesh domain was defined from bathymetric data provided by the Colombian Hydrographic Service (Servicio hidrográfico Colombiano - CIOH). Data obtained from the AG95.1 Model (Grenoble) were used for calculating the astronomical tide (AT) in the boundaries of the computational mesh. This model generates astronomical tide data worldwide [19]. Atmospheric pressure and wind data from the NOAA NARR (North American Regional Reanalysis) Database, extracted from the same computational mesh domain, were employed for estimating the meteorological tide (MT).
Synthetic sea level series were simulated using in-situ measurements of sea level obtained through pressure sensors deployed in the study area (Figs. 1B and 1C) and the model boundary conditions (AT + MT). The simulated series comprise the same period in which the pressure sensors were deployed in the Cartagena Bay (May 18th to June 18th of 2011) and the Urabá Gulf (February 26th to March 27th of 2010). Several combinations of roughness, friction and drag wind coefficients parameters were used for establishing the best fit between the real and simulated series.
Once model validation was completed, sea level series over 20 years were simulated in different sites within the study area. These series were fit using different probability functions (e.g. Log Normal, Normal, Weibull, Gumbel). The Normal and Gumbel distributions exhibited the best fit for the mean and extreme regimes, respectively. This approach allows determining sea level regimes in zones where records are scarce or unreliable.
2.1. Model equations
To generate the astronomical tide and the meteorological data series in the Gulf of Urabá and the Bay of Cartagena, a hydrodynamic model was used to solve the nonlinear equations of long waves, implying that L >> h, where L is the wavelength and h the depth at which it propagates. The long-wave condition can be considered applicable from L> 20 h [20].
Under this consideration, the flow is essentially horizontal. Thus, the horizontal velocity components (u and v) are much greater than the vertical component (w). This claim is valid, except in local areas with steep slopes (> 1/5) or where outcrops (upwelling), subsidences (downwelling) or oceanic fronts occur [21].
Horizontal flow consideration simplifies the general equations of motion also known as Navier-Stokes, allowing the elimination of the vertical component (w) and establishing a hydrostatic pressure distribution where the equation ∂p ∂z =−ρg can be integrated in depths from z to 𝜂 and expressed as:
where 𝑃 (𝑛) is the atmospheric pressure, 𝑃 𝑧 the hydrostatic pressure, 𝜂 the free surface level, 𝜌 the density and g gravity.
The depth-averaged equations of continuity and momentum lead to the following expressions:
where U is the fluid velocity in direction x, V is the fluid velocity in direction y, η is the free surface, 𝐻=ℎ+𝜂 is the mean depth, 𝐶 𝑎 is the wind drag coefficient, W is the wind speed 10 meters above the sea surface, 𝜓 is the angle between the wind direction in y x, C is the friction coefficient of Chezy, 𝜀 is the coefficient of turbulent viscosity, g is the acceleration of gravity, x is the horizontal coordinate, y is the vertical coordinate, t is time, and 𝑓 𝑐 is the Coriolis acceleration.
Eq. (2) is the equation of the continuity of fluid. Eqs. (3), (4) are the quantity of movement of the fluid at x and y respectively. The left side represents local and advective acceleration control volume and the right side represents the forces that induce or restrict these accelerations. These gradient forces are the free surface, the surface tension due to wind, bottom friction, the effect of turbulence, and the effect of the rotation of the earth, respectively [20]. The way in which the model solves the Eqs. (2)-(4) is by using a finite difference algorithm that is implicit in the alternating direction of double scanning [22].
2.2. Viscosity coefficients of Eddy, friction and wind drag
The coefficients of friction of Chezy (C), eddy viscosity coefficient (ε) and wind drag coefficient (Ca), present in the eq. (2)-(4), were used for model calibration. These coefficients rely on a wide range of factors; such as, bathymetry, roughness, properties of the bottom sediments, flow conditions, wind speed, etc. These factors are in turn dependent on the site or location and will vary with time. The uncertainty of the behavior of two-dimensional flow is concentrate of these parameters [21].
The eddy viscosity coefficient (ε) is used to describe turbulence, including several terms ranging from numerical dispersion caused by the transformation of differential equations in finite-difference equations that correspond to the average of vertical flow equations. In this case, a constant value of the eddy viscosity is set for the two points of study, which is used throughout the entire grid domain of the model. This condition is close to real conditions when the depth is much less than the discretization used, since in such situation the friction at the bottom is more important than turbulence. According to [23] the value of the eddy viscosity depends on the dimensions of the cells and its value can be calculated by using the following formula:
Where the surface roughness is between 0.05−0.15 , ∆𝑥 is the cell size (m) and u is the characteristic velocity (𝑚 𝑠 −1 ). In the case of the Bay of Cartagena study, the grid has a cell size ∆𝑥=150𝑚; taking the characteristic velocity as 𝑢=1 𝑚 𝑠 −1 , the value of 𝜀 ranges between 7.5 and 22.5 𝑚 2 𝑠 −1 . For this case a value of 𝜀=10 𝑚 2 𝑠 −1 was used, which, after various tests performed in the present work, fits the results better. In the case of the Gulf of Urabá study, the grid has a cell size of ∆𝑥=200𝑚; thus taking the characteristic velocity as 𝑢=1 𝑚 𝑠 −1 , the 𝜀 value oscillates between 10 and 30 𝑚 2 𝑠 −1 .A value of 10 𝑚 2 𝑠 −1 was selected, the same as in the case of Cartagena.
The seabed friction ratio refers to the dissipation of a quantity of flow movement by friction at the contours or the seabed. The parameter used in the model to represent this effect is the Chezy coefficient which has a value between 45 and 60 𝑚 𝑠 −1 in nearshore areas. The equation used by the model to define the friction coefficient based on seabed roughness is:
where K is the roughness in meters that represents seabed roughness, due to the size of the sediment and the shape of the floor [24-28] and H is a function of depth. The K value taken for both case studies was 0.01 m based on several tests performed in this study, in which the value of this coefficient was determined with optimal results.
Wind friction is triggered by the shear stress exerted by the wind on the surface of the ocean. It is represented by the equation:
In this equation, the wind drag coefficient of 𝐶 𝑎 [29] analyzes numerous measurements, concluding that in stable atmospheric conditions 𝐶 𝑎 depends linearly on wind speed. However, does not exist a universal formulation for the drag coefficient 𝐶 𝑎 , therefore it is necessary to perform adaptations whit instrumental data bases to validate a specific zone. In this case we define the drag coefficient as 𝐶 𝑎 =0.023 for both areas tested, according to the calibration results obtained.
2.3. Initial and boundary conditions
Series of astronomical tides were generated using data obtained from an interpolation method based on the AG95.1 model developed by [19], using the Grenoble database. These series were used as boundary conditions within the long-wave model, establishing periods coinciding with measurements made using tide-gauges in the Bay of Cartagena and the Gulf of Urabá. In Cartagena Bay a database was generated from the 18th of May 2011 to the 18th of June 2011 (Fig. 1B). In the Gulf of Urabá a database was generated for the period from the 27th of February 2010 until the 26th of March 2010 (Fig. 1C).
Two independent grids were generated for the application of the numerical model. In the Bay of Cartagena with a cell size of 150 m (Fig. 1B) and in the Gulf of Urabá with cell size of 200 m (Fig. 1C). These grids were generated from available nautical bathymetry charts and detailed bathymetric surveys developed by the Caribbean Center for Oceanographic and Hydrographic Research. They were complemented with global bathymetric information obtained from ETOPO 1, a NOAA (National Geophysical Data Center) database with a resolution of one minute for the Caribbean Sea area of Colombia.
The sea level variation also depends on the contribution made by meteorological tides (wind and pressure). These parameters were included as input conditions, obtaining the respective data-sets from the global database of NOAA’s NARR, on the same date in which data from tide-gauge was obtained. Atmospheric pressure and wind are implicit in the long-wave equations of the H2D hydrodynamic model. In addition, the inclusion of the effect of the tidal regime was necessary to determine the coefficient of wind drag (Ca). Through repeated executions of the model, varying the value between 0.019 and 0.025, the coefficient of wind drag that best fitthe simulated data to real conditions was Ca = 0.023.
2.4. Adaptation and calibration of the hydrodynamic model
To calibrate the model, the synthetic sea level series were compared with data measured by tide-gauges in the areas of study. The wind drag coefficient (Ca), Chezy friction (C) and turbulent viscosity (ε) were configured in the model to find the best statistical fit between the two series and to later generate synthetic sea level series with an extension of 20 years at each of the points observed in Fig. 1B and 1C. The mean and extreme regimes were extracted from this data through cumulative probability distribution and Gumbel extreme value distribution respectively for the current study. The Nash-Sutcliffe efficiency test (NSE) was employed for estimating the accuracy of the calibration. NSE indicates how well the observed data versus simulated data fits a 1:1 line, and is computed as shown in Equation 8:
where the model simulation can be judged as satisfactory if NSE >0.5 [30]
2.5. Determination of the mean sea level regime
A hydrodynamic calibrated (astronomical tide + meteorological tide) model allows simulate periods of 20 years (1991-2010) at various points in the study areas to determine the mean sea level regime. These mean sea level regimes represent the mean sea level behavior in terms of probability. Thus, different probability functions were evaluated, including Log Normal, Normal, Weibull, and Gumbel. Finally, the Normal distribution function provided the best statistical fit to the synthetic tidal series generated in the study areas.
2.6. Determination of the extreme sea level regime
To determine the extreme sea level regime the synthetic series were fit to a probability function. In this case the function allows the calculation of return periods and probabilities of non-exceedance of a sea level height determined from a set of independent extreme values over time. Once these extreme values were determined, and they were split into annual series to subsequently fit them to a distribution function. In this case, the Gumbel maximum distribution function provides the best statistical fit.
3. Results
The following shows the comparisons between measured and simulated time series of sea level within the study areas. In the first instance the measured time series of sea level were compared with simulated series of astronomical tides. Then, the effects of wind and atmospheric pressure (meteorological tide) in the modeled data were incorporated. Through this process a best fit between the measured data and the modeled data was obtained.
3.1. Sea level calibration (AT + MT) in the bay of Cartagena and the gulf of Urabá
For both study areas, comparisons were performed between the mean sea level measured by tide-gauges (AT + MT) and the astronomical tide, considered as the only input condition for the hydrodynamic model. The modeled astronomical tide resembles the patterns exhibited by the mean sea level signal measured in both areas, the Bay of Cartagena (Fig. 2) and the Gulf of Urabá (Fig. 4).

Source: The authors.
Figure 2 Comparison of modeled astronomical tide vs. sea level recorded by the tidal gauge in the Bay of Cartagena.
NSE analyses were performed between the modeled and measured sea level time series to determine in greater detail the fit of the model outputs to the real conditions. NSE coefficients of 0.82 and 0.63 were obtained for the Bay of Cartagena (Fig. 3) and Urabá (Fig. 5), respectively.

Source: The authors
Figure 3 Linear comparison between the simulated astronomical tidal series and sea level recorded by the tide gauge in the Bay of Cartagena. The Nash-Sutcliffe efficiency test shows a good agreement between both series.

Source: The authors
Figure 4 Comparison of modeled astronomical tide vs. sea level recorded by the tide gauge in the Gulf of Urabá.

Source: The authors
Figure 5 Linear comparison between the simulated astronomical tidal series and sea level recorded by the tide gauge in the Gulf of Urabá.
After obtaining statistical significant results in modeling the astronomical tide as the only input condition of the hydrodynamic model, the variations in sea level caused by the meteorological tide (wind and pressure) was added to simulate synthetic sea level series; and thus, to improve the correlation between the measured and simulated time series.
Similarity patterns of the measured and modeled time series were improved by almost a 3%, because this approach include the effect of atmospheric pressure and wind intensity within the modeling parameters (Figs. 6, 8). The NSE coefficient estimated for the Bay of Cartagena increased to 0.85 (Fig. 7), whereas the correlation coefficient in Urabá rose to 0.66 (Fig. 9).

Source: The authors
Figure 6 Comparison of modeled sea level (AT + MT) vs. signal extracted from the gauge in the Cartagena area.

Source: The authors
Figure 7 Linear comparison between the simulated series (AT + MT) and sea level taken from the gauge in the Cartagena area.

Source: The authors
Figure 8 Comparison of modeled sea level (AT + MT) vs. signal extracted from the gauge in the region of Urabá.
3.2. Mean sea level regime (AT + MT) in Cartagena bay and the gulf of Urabá
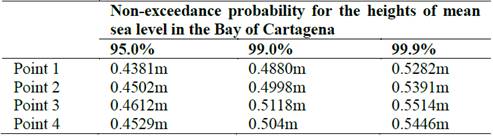
The determination of the mean regime, as indicated above, is the mean behavior of sea level over a period. In this case, for a period of 20 years (1991-2010) for each of the points located in the areas of study. In the Bay of Cartagena (Fig. 1B) four points were used for determining the mean sea level regime (i.e. two on the north side, P2 and P1, and two more inside the bay on the south side, P4 and P3). The results are shown in Fig. 10. For this area, the mean sea level regime amounts to 0.43 and 0.55 m for non-exceedance values between 95% and 99.9%, respectively, as shown in Table 1.

Source: The authors
Figure 10 Mean sea level regime for the modeling point distribution in the Bay of Cartagena, zoomed at the top of the graph to see better results.
Table 1 Values of non-exceedance probability of the heights of mean sea level in meters, for 95%, 99% and 99.9% in each of points in the Bay of Cartagena.
Source: The authors
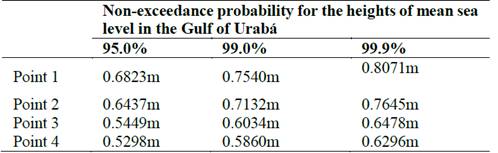
Four points were selected to estimate the mean sea level regime in the Gulf of Urabá. Two points in the south of the Gulf (P1 and P2), one in the center of the Gulf (P3), and one closer to the north of the Gulf (P4) (Fig. 1C). The mean sea level regime results in this area (Fig. 11) were 0.52 and 0.80 m for non-exceedance values between 90% and 99.9%, respectively, as shown in Table 2.

Source: The authors
Figure 11 Mean sea level regime for the modeling point distribution in the Gulf of Urabá, zoomed at the top of the graph to see better results.
Table 2 Values of non-exceedance probability of the heights of mean sea level in meters, for 95%, 99% and 99.9% in each of points in the Gulf of Urabá.
Source: The authors
The annual maximum method was used to determine the extreme sea level regime in Cartagena Bay and the Gulf of Urabá. This method divides the time series annually by selecting the maximum values of that variable over time. Thus, obtaining a continuous series of independent extreme values through time. Once these extreme values were determined, the Gumbel distribution function was applied to determine the return periods of sea level heights in the areas mentioned above. The extreme sea level regime is presented as the result of a maximum Gumbel probability, in which sea level is shown in meters and the return period in years for both study areas (Figs. 12, 13).
3.3. Extreme sea level regime in the bay of Cartagena and the gulf of Urabá
The Bay of Cartagena (Fig. 12) exhibits levels of 0.55 m for a return period of 10 years and 0.63 m levels for a return period of 100 years as extreme behavior of sea level at the selected points, whereas, for the Gulf of Urabá area (Fig. 13), the extreme sea level is to 0.66 m for a return period of 10 years and 0.88 m for a return period of 100 years.

Source: The authors
Figure 12 Return period of the heights of sea level in the Bay of Cartagena in search points P1, P2, P3 and P4.
4. Discussion
The methodology for estimating sea level patterns did not consider the effects of rivers discharging into Cartagena Bay and Urabá Gulf, due to the lack of reliable streamflow data on a high resolution time-scale, mainly for the latter. Therefore, the results of this study only represent the contribution of the astronomical and meteorological tides, ignoring fluvial effects.
The sea level in the Bay of Cartagena, according to the results of this study, varies between 0.528 m and 0.551 m (values representing the 99.9% of not exceeding -Table1), consistent with [31], which asserted that the Caribbean Sea exhibits a microtidal range (astronomical tide) ranging from 0.2 to 0.4 m, depending on the geographic location. This range lie below our estimates for the Cartagena Bay (0.528 and 0.551 m). However, these estimates include the additional rise caused by wind and atmospheric pressure (meteorological tide).
The extreme regime of the Cartagena Bay exhibited a slight increase inside the Bay (P3 and P4 points), in comparison with the extreme regimes observed in P2. The internal sector (P4) exhibits values of 0.58, 062 and 0.65 m, corresponding to 10, 25 and 50-yrs return periods, respectively. Whereas the external sector (P2) show values of 0.53, 0.56 and 0.59 m, corresponding to 10, 25 and 50-yrs return periods, respectively. Tidal gauge data located in the Bay of Cartagena referred to by [32,33] were not used for this study because there is a large quantity of gaps in the seasonal sea level records. In addition, this gauge has been located in different places within the Bay of Cartagena which resulted in a change of the reference level at each point.
The mean and extreme sea level regimes in the Urabá Gulf increase southward. At P4, located in the North of the gulf, the range of the mean regime was 0.65 m; whereas at P1, located in the southernmost part, this range rises up to 0.82 m. This pattern was also observed in the extreme regime. P4 exhibited extreme values of 0.59, 0.61 and 0.63 m for return periods of 10, 25 and 50 years, respectively; while, P1 exhibited extreme values of 0.85, 0.87 and 0.89 m for those return periods, respectively. This pattern might be linked to tide superposition, since tides can be described as overlapping waves, in which the interaction of incoming and outgoing tides increases due to reflection at the boundaries; which in turn, leads to a rise in sea level oscillations according to the gulf setting (i.e. depth and length) [34].
The improvement in the statistical adjustment caused by meteorological tide contribution is nearly 3%. Such improvement might be considered to be negligible. Nevertheless, it must be considered that in extreme conditions, atmospheric pressure and wind contributions might be significant. Therefore, this study considered both factors as key parameters when estimating sea level regimes in the Colombian Caribbean. The statistical model seems is to the underestimate the values of the sea level when comparing to instrumental records measured near Capurganá - Urabá Gulf (Fig. 1C). Such underestimation may be induced by the low spatial resolution of the bathymetric data in this zone, which impedes a proper signal representation of the tides.
In addition, the fit between the simulated and observed meteorological tide signals might be further enhanced. This is mainly because we assume a single value of wind and atmospheric pressure for each time step along the entire grid employed in the H2D model. Due to its spatial resolution (32 km) just one or two points of the NARR database of wind and atmospheric pressure coincided with the grids employed in this study. These coinciding points were used to define grids with the same spatial resolution as that of the grids employed in the Cartagena Bay and Urabá Gulf. Consequently, a larger discretization of the wind and atmospheric pressure fields, as a model input, would improve the modelling results. It was determined that at the southern end of the Gulf of Urabá, the mean sea level regime was characteristically rise relative to sea level values found in the Cartagena Bay by 67%, due to the marked effect of sea level rise produced by the configuration of the gulf. It was found that sea level values in the southern Gulf of Urabá reach 0.807 m, which differ from other known tidal ranges in Colombia’s Caribbean region, as determined in previous studies.
The results of the mean and extreme regime determined by the proposed method serve as a statistical tool for defining technical control criteria, design, construction and programming of the design and use of coastal and port protection structures. Future research should include the streamflow effects (mainly in semi-enclosed areas such as bays and gulfs) when determining the sea level regime.
It is also recommended that wind and atmospheric pressure databases (from measurements or Reanalysis) with greater spatial resolution to obtain a better simulation of the meteorological tide regime in the surveyed areas (Cartagena Bay and Urabá Gulf).
5. Summary and conclusions
A method was established for reconstructing mean and extreme sea level regimes in microtidal areas where there are no historical instrumental records of sea level. This was done through the calibration and numerical simulation of sea level data sets considering the effects of astronomical tide and meteorological tide. This method was validated in two areas of Colombia’s Caribbean coast. It was found that simulated sea level results fit better to the measured instrumental data when the initial conditions of the effect on tide levels from weather and wind pressure are included in the model. The mean sea level regime, both within and outside the Bay of Cartagena, did not vary significantly. In the south of the bay, slight changes in the values of extreme ranges were due to the appearance of compound tides, although in the results this effect was not very pronounced.
























