Evaluación y zonificación de la amenaza por movimientos en masa en suelo rural

Análisis de la amenaza por lluvia en suelo rural: la amenaza por movimientos en masa se relaciona con el grado de probabilidad de ocurrencia en una zona determinada y un periodo específico (^{Varnes, 1984}). Según ^{Erener y Düzgün (2013)}, la amenaza (H) puede ser calculada como el producto entre dos probabilidades: la probabilidad de que se supere un cierto umbral (P _t ) y la probabilidad de ocurrencia de proceso de ladera en dicha región (P _f ).

Donde la probabilidad P _f puede ser formulada como:

Donde P _s es la probabilidad espacial de un movimiento en masa y P _l |P _t es la probabilidad condicionada de tener un movimiento en masa si un evento de lluvia detonante supera un valor de un umbral para un periodo determinado. Por lo tanto, la amenaza se puede estimar para un tiempo t como la siguiente probabilidad:

A continuación, se describe el método para estimar la probabilidad espacial (P _s ) a través del análisis de susceptibilidad, y, dado el factor detonante lluvia, el método implementado para estimar la probabilidad que supere el umbral (P _t ) y la probabilidad condicionada de tener un proceso de ladera (P _l |P _t ).

Evaluación de la susceptibilidad (P _s ) previo a la implementación de los métodos de susceptibilidad, se requiere realizar un mapa de procesos morfodinámicos y la selección de variables.

Inventario histórico de eventos: puede ser realizado con base en fuentes de datos que tienen cobertura en el territorio colombiano: Sistema de Inventarios de Desastres (Desinventar) (http://www.desinventar.org) y Sistema de Información de Movimientos en Masa (SIMMA) (http://simma.sgc.gov.co). También existen bases de datos internacionales que pueden ser consultadas.

Fotointerpretación multitemporal: técnica mediante la cual se definen las condiciones geológicas y geomorfológicas, y se delimitan algunas áreas pobladas y usos del suelo. Las fotografías pueden ser tomadas de diferentes fuentes, tales como el Instituto Geográfico Agustín Codazzi (IGAC), las corporaciones autónomas regionales (CAR), el SGC, las oficinas de catastro, entre otros, a diferentes escalas coherentes con la escala de trabajo 1:25.000 y de años distintos.

Levantamiento de campo: toma de información a través de una campaña de campo de verificación del mapa fotogeológico, geomorfológico y de procesos morfodinámicos. De allí, se establece el grado de actividad de cada proceso en el momento del levantamiento (activo, latente, relicto o inactivo).

• Variables condicionantes

Hace relación a la definición de variables que directa o indirectamente influyen en el desarrollo de movimientos en masa, y son definidas como las propiedades internas e inherentes del terreno que promueve la ocurrencia de procesos de ladera (^{van Westen etal., 2008}; ^{Corominas et al., 2014}). Se utilizan, entre otras, como variables condicionantes:

Geología (GE): la geología del territorio puede inicialmente ser tomada de las planchas oficiales realizadas por el SGC a nivel regional, llevadas a la escala de trabajo a partir de estudios complementarios que se hayan realizado, bien sea por parte del mismo municipio o en estudios previos de otras entidades. También, es necesario llevar a cabo campañas de campo de verificación, validación y actualización de la información.

Coberturas vegetales (CO): puede ser realizado a partir de imágenes Rapideye, a través de un procesamiento visual y digital de las imágenes, mediante clasificaciones supervisadas y no supervisadas a una resolución espacial mínima, de acuerdo con las imágenes que se obtengan. Los resultados de este proceso pueden ser validados con mapas de coberturas vegetales del plan básico de ordenamiento territorial (PBOT) antiguos o del IGAC.

Pendiente (PE): para determinar la pendiente de la superficie del terreno, es decir, el ángulo entre esta y la horizontal, se puede emplear el algoritmo de ^{Jones (1998)}, el cual puede ser implementado en softwares de sistemas de información geográfica (GIS) y modelos de elevación digital (MED), disponibles en el IGAC, oficinas de planeación o del programa ALOS-PALSAR (https://asf.alaska.edu/data-sets/sar-data-sets/alos-palsar/), con resolución de 12,5 m.

Aspecto (AS): esta variable evidencia la dirección de la pendiente y la influencia de la luz solar en el terreno. Es calculada usando la derivada parcial de la elevación respecto a las direcciones X y Y. Es evaluada en forma circular por lo que da posición cardinal: norte, sur; este, oeste (^{Dai et al., 2001}).

Relieve relativo (RR): se expresa como la máxima diferencia entre la mayor y la menor elevación por metro.

Inclinación de la ladera (IL): se refiere a la inclinación, en términos de porcentaje, de las laderas del territorio de análisis. Puede ser determinada a partir de GIS.

Elevación relativa al cauce (EAS): se debe calcular como la elevación de cada celda de la cuadrícula en un ráster por encima de la celda de flujo más cercana.

Curvatura (CU): establece el nivel de convexidad (valores negativos) o concavidad (valores positivos) de la superficie, y define el rol de la topografía para condensar o diseminar el mayor valor registrado de eventos de lluvia en un sector específico de la ladera.

Rugosidad (RU): define la variación de la inclinación de una zona, y se relaciona con el grado de desviación del vector normal a la superficie de cada celda, expresando así la complejidad y ondulación del terreno. Cuando la rugosidad es igual a 1, se interpreta como nula; estos valores disminuyen conforme se incrementa la dispersión de los vectores.

Índice de posición topográfica (TPI): es un índice topográfico compuesto. Evalúa morfología en la posición relativa del cauce, y arroja la diferencia entre un valor de elevación de celda y la elevación promedio del vecindario alrededor de esta. Valores positivos reflejan una mayor elevación de la celda respecto a su entorno, mientras que los valores negativos significan que es más bajo.

Índice de humedad topográfico (TWI): evalúa el grado de propensión a la acumulación de agua (^{Gruber y Peckham, 2009}); relaciona la humedad edáfica y la tendencia del suelo con la generación de procesos de escorrentía.

• Análisis exploratorio de variables El grupo de variables, cuyo comportamiento incide directa o indirectamente en el desarrollo de movimientos en masa, está condicionado por la escala de análisis, sumado a las propiedades del área de interés y al tipo de movimientos en masa. Cada zona cuenta con unas propiedades en particular. Para la selección de las variables, se utiliza la correlación lineal entre variables a través del método de Spearmen, el cual permite encontrar similitudes entre las variables, y el método de análisis de frecuencia de variables (^{Lee et al., 2008}), que refleja cómo es la conducta de cada variable bajo condiciones de aparición o no de movimientos en masa. Esta comparación permite seleccionar aquellas que mejor clasifican la ocurrencia y no ocurrencia de procesos de ladera, mejorando la eficiencia, desempeño y capacidad de predicción del modelo.

Una vez es determinada la anterior información, se puede proceder con la implementación de los métodos para la evaluación de la susceptibilidad. Para el área rural, se pueden usar dos metodologías independientes. La primera, el método estadístico multivariado, denominado regresión logística (^{Atkinson et al., 1998}; ^{Gorsevski et al., 2006}), corresponde al método más ampliamente utilizado en el mundo. La segunda metodología incluye el método recomendado por el Servicio Geológico Colombiano (^{SGC, 2017}), correspondiente al peso de la evidencia, el cual, combinado con el análisis jerárquico de procesos (AHP) que asigna los valores a las variables, permite obtener un método híbrido (^{van Westen, 1993}; ^{Ayalew et al., 2004}; ^{Süzen y Doyuran, 2004}).

• Método híbrido

El método híbrido corresponde al uso del análisis multivariado para la asignación de pesos a las variables, mediante el análisis jerárquico de procesos (AHP), combinado con el método estadístico bivariado peso de la evidencia (WoE) para asignar peso a las clases. A continuación, se describe cada uno de los métodos.

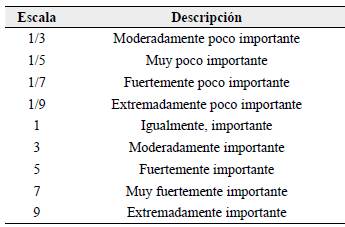
Método análisis jerárquico de procesos (AHP): método heurístico de toma de decisiones multicriterio, que permite convertir la relativa importancia de los factores condicionantes en la ocurrencia de movimientos en masa, a partir de evaluaciones subjetivas de expertos (^{Saaty, 2001}). Se utiliza una matriz de comparación entre las variables condicionantes, a partir de la escala de evaluación e importancia propuesta por Saaty (1980), con valores de 1 a 9 (Tabla 1).

Método peso de la evidencia (WoE): está fundamentado en la teoría de la probabilidad bayesiana, en la cual se examina el vínculo existente entre dos eventos, realizando la manipulación probabilística de condiciones (^{Olshausen, 2004}), que, particularmente para los movimientos en masa, concierne a la correspondencia entre las zonas perjudicadas por los movimientos en masa y la distribución espacial de los factores condicionantes de la zona (^{Regmi et al., 2010}; ^{Sujatha et al., 2014}). En este método, se requiere calcular el peso de cada una de las clases que constituyen las variables condicionantes (^{van Westen et al., 2003}). Este valor denota el grado de incidencia de la categoría como parámetro en el desarrollo de eventos de remoción en masa (Regmi et al., 2010; ^{Oh y Lee, 2011}).

Los pesos asignados pueden ser valores positivos (W+), lo cual refleja que la existencia de esta clase comoparámetro favorece el desarrollo de movimientos en masa, y su magnitud permite interpretar el grado de correlación, y negativos (W) que reflejan la inexistencia de la clase i. Cuando el valor corresponde a cero, se interpreta que no es relevante para la ocurrencia del movimiento en masa (^{Dahal y Hasegawa, 2008}; ^{Regmi et al., 2010}). Para el cálculo de estos pesos, se utilizan las siguientes expresiones:

Donde A1 es la cantidad de pixeles con movimientos en masa en la clase; A2, cantidad de pixeles con movimientos en masa que no existen en la misma clase; A3, cantidad de pixeles en la clase con ausencia de deslizamientos; y A4 es la cantidad de pixeles en la clase donde no se registran movimientos en masa y que además no están presentes en la misma clase (^{Ozdemir y Altural, 2013}).

El peso final o peso de contraste (W _f ) es la diferencia entre los dos pesos, el cual indica la medida de correlación entre el deslizamiento y la clase de la variable condicionante analizada (^{SGC, 2017}).

Con los pesos respectivos de las variables condicionantes (B _n ), obtenidos mediante el método AHP, y los pesos de cada clase (X _n ), obtenidos mediante el peso de contraste W _f , se estima la susceptibilidad (z _W ) para cada celda, utilizando la siguiente ecuación:

• Modelo de regresión logística (RL)

Se define como un método estadístico multivariado que permite establecer el vínculo entre variables dependientes (desarrollo de movimientos en masa) de valores dicotómicos que representan la no ocurrencia (valor igual a 0) o la ocurrencia (valor igual a 1) del evento, con las variables independientes, puntualmente las que se denominan predictoras o condicionantes del terreno. La RL tiene como beneficio que las variables predictoras no necesitan presentar una distribución normal, además de poder ser discretas o continuas o una mezcla de ambas (^{Atkinson et al., 1998}).

El vínculo de dependencia entre el desarrollo de movimientos en masa y las variables es calculado mediante la siguiente expresión:

Donde P(y) es la probabilidad espacial estimada del desarrollo de movimientos en masa y puede adquirir valores en un intervalo de 0 a 1. Y corresponde a una combinación lineal de las variables independientes:

Donde b₀ es el intercepto del modelo según el método de RL; los valores b _i (i=1, 2, 3.....n) son los coeficientes de la regresión logística, es decir, los pesos de las variables, y los valores x _i (i=1, 2, 3.....n) son las variables independientes.

La RL constituye uno de los métodos estadísticos multivariados más usados para calcular la susceptibilidad por movimientos en masa a escalas medias a regionales (^{Ayalew y Yamagishi, 2005}; ^{Lee y Pradhan, 2007}). Para ejecutar el método de RL se puede hacer uso del software SPSS del IBM, al cual se le ingresa un valor aproximado al 80% de los movimientos en masa del mapa de inventario compilado, y se selecciona aleatoriamente la misma cantidad de pixeles que no desarrollarán procesos de ladera. Esto, con el objetivo de reservar el 20% restante del inventario para obtener, al final, la capacidad de predicción del modelo.

Realizado lo anterior, se obtiene la información necesaria para la zonificación de la susceptibilidad.

• Mapa de susceptibilidad

En primer lugar, es necesario evaluar el desempeño y predicción de un modelo para realizar su aceptación o rechazo, debido a la presencia de diversos factores que pueden introducir incertidumbre al proceso de evaluación de la susceptibilidad y amenaza por movimientos en masa. Por lo anterior, se introduce el término de desempeño, el cual es definido por la Australian Geomechanics Society, AGC (^{Fell et al., 2008}), como la capacidad del modelo para describir el comportamiento del sistema y su sensibilidad ante cambios en los parámetros de entrada, además de la capacidad para predecir con exactitud los datos observados. Para ello, se implementan los métodos curva de éxito y curva de predicción (^{Davis et al., 1990}; ^{Chung y Fabbri, 2003}), área bajo la curva (AUC) (^{Fawcett, 2006}; ^{Carvalho et al., 2014}) y matriz de confusión (^{Chevalier et al., 2013}).

Evaluación del modelo de susceptibilidad: se debe analizar el rendimiento y ajuste del modelo con el registro de movimientos en masa utilizado, y con ello determinar si se obtiene un buen desempeño y capacidad de predicción del modelo escogido. Adicionalmente, al modelo definitivo de susceptibilidad por movimientos en masa se le debe calcular la matriz de confusión, que es un procedimiento de validación adicional que brinda la posibilidad de contrastar las observaciones elaboradas en el inventario de movimientos en masa con las predicciones del modelo.

Los aciertos del modelo, es decir, las celdas que este arroja como amenaza alta y que efectivamente en el mapa de procesos así figura, son denominados un "verdadero positivo". Los "verdaderos negativos", por su parte, corresponden a las zonas identificadas como de susceptibilidad baja o media por el modelo y que no presentan movimientos en masa en el mapa de procesos.

Entre tanto, el error del modelo se puede evaluar a través de los "falsos positivos", que son aquellas celdas donde aparecen movimientos en masa en el inventario y que en el mapa obtenido presentan susceptibilidad media o baja. Por último, los "falsos negativos" son aquellas celdas que presentan susceptibilidad media o baja y que cuentan con movimientos en masa según el inventario de procesos.

Análisis del factor detonante lluvia (P _l |P _t y P _t ): la precipitación, especialmente en zonas montañosas tropicales, es el principal factor detonante de movimientos en masa (^{Aristizábal et al., 2011}). Para estimar la probabilidad de que el evento de lluvia exceda un umbral crítico definido (P), y la probabilidad condicionada de que ocurra un movimiento en masa para el caso en que el umbral de lluvia (P _l |P _t ) sea superado, se utilizan metodologías empíricas y estadísticas propuestas por autores como ^{Glade et al. (2000)} y ^{Guo et al. (2013)}, las cuales se basan en inventarios históricos de movimientos en masa y registros históricos de precipitaciones.

Para este análisis se emplean los mismos inventarios históricos de movimientos en masa que fueron utilizados para el mapa de procesos morfodinámicos (DesInventar y SIMMA), mientras que las series de precipitación son construidas a partir de la información disponible en las estaciones meteorológicas del IDEAM presentes en el municipio y sus alrededores, que posean información de precipitación histórica; la selección de las estaciones debe ser realizada a partir de la continuidad de la información y el área de influencia de cada una, que, a su vez, es establecido con ayuda de polígonos de Thiessen.

Para la construcción de la base de datos, dado que es habitual que exista diferencia entre los periodos de actividad de las estaciones, y que, además, puede haber porcentajes altos de datos faltantes en algunas de estas, se puede crear para cada día de registro un solo dato de precipitación, resultado de promediar los valores de lluvia de otras estaciones que tienen información disponible de dicho día, asumiendo así un valor de precipitación constante en todo el municipio.

Posteriormente, se debe determinar, por regiones, el umbral mínimo de lluvia crítico, que representa el valor de precipitación por encima del cual la probabilidad de ocurrencia de un movimiento en masa aumenta significativamente, y el umbral máximo de lluvia, que consiste en las condiciones de precipitación, bajo las cuales se ha producido la mayor cantidad de eventos (^{Glade, 2000}). Para ello, se debe realizar un análisis de umbrales de lluvia acumulada (LA), es decir, el valor correspondiente a la precipitación registrada en los días inmediatamente anteriores al evento, y lluvia acumulada antecedente (LAA), que refleja el valor asociado a la lluvia acumulada en las fechas precedentes a los definidos como lluvia acumulada (LA) (^{Aristizábal et al., 2011}).

Se puede realizar la correlación de LA de 1, 3, 5, 7 días y la LAA de 15, 30, 60 y 90 días para cada uno de los días que exista información histórica; a cada uno se le asigna el respectivo número de movimientos en masa ocurridos. Finalmente, se establece una separación entre las precipitaciones que no ocasionaron movimientos en masa de aquellos que ocasionaron uno o más, estableciendo la combinación de LA y LAA que más condiciona el desarrollo de deslizamientos y el umbral de lluvia para cada rango de tiempo en el municipio.

Por último, con LA y LAA determinados, se calcula la probabilidad de ocurrencia del movimiento, dado que el umbral de lluvia crítico de LA y LAA se sobrepasa ((P _l |P _t ) x P _t ). Los umbrales son usados para construir las curvas de excedencia que permitan calcular la probabilidad de que cierta cantidad de lluvia acumulada en los días definidos por los umbrales sea alcanzada o superada (P _t ) y la probabilidad de que suceda un evento cuando dicha cantidad de lluvia acumulada sea alcanzada (P _l |P _t ).

• Verificación heurística y mapa de amenaza por movimientos en masa Ahora bien, con las probabilidades P _s , P _l |P _t y P _t determinadas, se obtiene el nivel de amenaza por movimientos en masa (H), con base en la expresión que las relaciona, la cual fue determinada según la metodología adoptada.

Para la realización del mapa de amenaza, se deben seguir las recomendaciones del Decreto 1807 de 2014; según estas, pendientes con valor inferior a 5° y sin evidencias de susceptibilidad se consideran categoría baja, mientras que las zonas con presencia de procesos activos, se considera en la categoría alta.

Posteriormente, es necesario realizar la verificación heurística, pues dicho mapa es el resultado de la implementación del modelo estadístico, el cual está en función de los datos de entrada y las incertidumbres que presentan cada una de ellas. Considerando esto, se realiza un ajuste heurístico con criterio de expertos, basados en los recorridos de campo y herramientas de sensores remotos como las fotografías aéreas y las ortofotos disponibles. Este ajuste se realiza en las zonas en las que el modelo predijo amenaza baja o media, pero que tienen las condiciones y evidencias manifiestas.

Análisis de la amenaza por sismo en suelo rural: el análisis del sismo como factor detonante de movimientos en masa es realizado a través del método de Newmark, que es un índice que permite entender cómo una pendiente podría comportarse durante un evento sísmico (^{Jibson et al., 2000}). El método requiere evaluar los siguientes parámetros:

Factor de seguridad:^{Jibson et al. (2000)} proponen un modelo de equilibrio límite de talud infinito en material friccionante y cohesivo para obtener el factor de seguridad mediante la siguiente relación:

Donde c' es la variable que representa la cohesión efectiva; Φ, el ángulo de fricción; y, el peso unitario de los materiales; θ, el ángulo asociado a la pendiente; t, el espesor del suelo normal a la pendiente; y_w, el peso unitario del agua; y m es la proporción del suelo que está saturado.

Para la obtención de los parámetros, es ideal realizar la obtención primaria de la información, no obstante, en caso de que no sea posible, se puede hacer uso de datos geotécnicos libres, como la base de datos Geotechdata. info que estima valores típicos de los parámetros basados en diversos estudios, teniendo en cuenta diferentes ensayos de laboratorio. Así, a partir del tipo de suelo generado por las unidades geológicas de la zona, según la Unified Soil Classification System (USCS, por sus siglas en inglés) (^{ASTM D2487-17}), se determinan los valores de cohesión c' (kN/m²), fricción Φ (°), peso unitario Yd (kN/m³) y permeabilidad k (m/s).

Aceleración crítica (a _c ):^{Newmark (1965)} mostró que la aceleración crítica de un bloque que potencialmente se puede deslizar depende del factor de seguridad estático y de la geometría del bloque, expresado como:

Donde α _c es la aceleración crítica en términos de g, la aceleración de la gravedad de la tierra; FS, el factor de seguridad, y θ el ángulo que forma la horizontal con el centro de masa del bloque, que generalmente se aproxima a la pendiente.

Aceleración máxima del terreno (PGA): es la amplitud de la aceleración más grande registrada en un acelerograma en un sitio durante un terremoto en particular. PGA es el parámetro de movimiento más simple a nivel de roca, por lo que no considera las posibles amplificaciones a lo largo del perfil de suelo. Finalmente, a partir de estos parámetros se calculan los desplazamientos de Newmark (Dn) a través de una regresión logarítmica estimada por ^{Jibson (2007)}:

Evaluación y zonificación de la amenaza por movimientos en masa en suelos urbanos y de expansión

La evaluación y zonificación de la amenaza en suelos urbanos y de expansión requiere de la obtención de los parámetros geotécnicos de cada uno de los sitios por analizar, los cuales describen las propiedades físicas y mecánicas del suelo, y, además, deben ser integrados como capas por medio de mapas ráster. Para ello, se caracterizan los suelos teniendo en cuenta información, tal como estudios de suelos realizados en el municipio y bibliografía; estos son clasificados y se ajustan según la geología, para acotar los parámetros geotécnicos que se utilizan en el análisis (cohesión c' (kN/m²), ángulo de fricción Φ' (°), peso unitario seco Yd (kN/m³) y coeficiente de permeabilidad k (m/s)).

Análisis de la amenaza por movimientos en masa detonados por lluvia en suelos urbanos y de expansión: para la evaluación de la amenaza en el área urbana y de expansión urbana se implementa el método determinístico y probabilístico con base física denominado r.slope.stability, desarrollado por ^{Mergili et al. (2014)} como un módulo ráster del software de código abierto GRASS GIS (^{GRASS Team, 2017}). Con este método se modelan dos escenarios de ocurrencia de movimientos en masa: i) deslizamientos superficiales, mediante un análisis determinístico utilizando el modelo de estabilidad de talud infinito, en el cual la superficie de falla se supone planar; y ii) deslizamientos profundos, mediante un análisis probabilistico, en el cual las superficies de falla son elipsoidales (^{Mergili et al., 2014}).

El modelo adopta el modelo geotécnico de ^{Hovland (1977)}, donde cada celda ráster es representada por una columna, la cual posee las características geotécnicas del suelo ingresadas por una serie de mapas ráster. El análisis hidráulico se realiza con el modelo tridimensional desarrollado por ^{King (1989)}, donde las fuerzas de infiltración trabajan en la dirección del gradiente hidráulico (análisis probabilistico), y las fuerzas de infiltración se consideran paralelas a la superficie, en el caso del análisis deterministico con el modelo de talud infinito.

El modelo probabilistico de r.slope.stability se caracteriza por considerar una serie de superficies de falla elipsoidales generadas aleatoriamente; estos elipsoides son restringidos en tamaño (longitud, ancho y profundidad) por el usuario. Cada superficie de falla elipsoidal atraviesa varias columnas (celdas ráster). En cuanto al análisis probabilístico, este utiliza distribuciones de probabilidad de densidad para cada uno de los parámetros geotécnicos (c', cp y profundidad), y determina la probabilidad de falla más alta y el factor de seguridad más bajo para cada columna, calculados con la siguiente ecuación.

Donde c' es la cohesión efectiva; A, el área de la superficie de falla; G' es el peso del suelo húmedo; β _c , la inclinación de la superficie de falla; φ', el ángulo de fricción interno; β _m , inclinación aparente de la superficie de falla en la dirección de la ladera (α); N _s y N _t son la contribución de la fuerza de infiltración normal y cortante, respectivamente (^{Mergili et al., 2014}).

Análisis de la amenaza por sismo en suelos urbanos y de expansión: para la evaluación de la amenaza por movimientos en masa detonados por sismo en áreas urbanas y de expansión, se propone el método pseudoestático. El método se fundamenta en el modelo de talud infinito, en el cual la unidad de análisis es un elemento vertical de ancho b y altura z. El factor de seguridad pseudoestático (F _ss ) se calcula teniendo en cuenta las condiciones naturales del terreno, más una fuerza lateral horizontal que actúa sobre la ladera, la cual depende del peso W del elemento vertical y del coeficiente sísmico k (^{Chowdhury et al., 2009}).

El cálculo del F _ss se realiza teniendo en cuenta una presión de poros u preevento sísmico, por lo que no se asume un exceso en la presión de poros durante el evento.

Donde:

Los valores para el coeficiente sísmico se basan en el análisis de registros históricos (Tabla 2). Para el caso de los municipios del territorio colombiano, se utiliza el k definido por la NSR-10, de acuerdo con el nivel de amenaza.

Definición de áreas con condición de riesgo y condición de amenaza

Mediante el cruce de los mapas de amenaza, obtenidos a través de las metodologías presentadas, con la cartografía del catastro municipal, es posible establecer las áreas con condición de riesgo y condición de amenaza, según los criterios mencionados en la normativa nacional.

Areas con condición de amenaza ACA: de acuerdo con el ^{Decreto 1807 de 2014}, las ACA corresponden a aquellas zonas donde no hay elementos expuestos y zonificadas en los estudios básicos de amenaza como alta y media, que se consideren como objeto de desarrollo. Es importante resaltar, como lo señala este mismo Decreto, que el desarrollo de dichas áreas dependerá de la información obtenida de los estudios detallados.

Areas con condición de riesgo ACR: de acuerdo con el Decreto 1807 de 2014, las ACR corresponden a las zonas urbanizadas u ocupadas del municipio, catalogadas con amenaza alta; se incluyen también aquellas donde se tenga presencia de infraestructura del sistema vial y de servicios públicos y equipamientos de dotación del sector salud, educación, entre otros. Asimismo, dentro de la categoría de ACR se debe incluir aquellas áreas con amenaza media, donde en la revisión o expedición del POT se proponga una variación de densidad o una modificación en los usos del suelo que pueda ocasionar o acrecentar el riesgo en el área.