Introduction
Native breeds are commonly used in sheep production systems in tropical regions of Latin America, mainly hair sheep for meat, such as Pelibuey, Black Belly, Katahdin, and Santa Inês (Chay-Canul et al., 2016). In Mexico, the most widely used maternal breed for sheep rearing is the Pelibuey (Chay-Canul et al., 2016; 2019a). These systems are characterized by minimal use of inputs, low or no application of modern technologies, and poor adoption techniques (Alexandre et al., 2021). Under these conditions, the constant evaluation of animal growth poses a major challenge for small producers, more so for measuring live weight (LW) due to the high cost of direct measurement equipment, such as livestock scales (Chay-Canul et al., 2019a; Canul-Solis et al., 2020; Sabbioni et al., 2020).
In terms of management, measurement of LW is important for designing nutrition and animal health programs (Sabbioni et al., 2020). Additionally, in meat sheep breeds LW is essential for choosing the optimal slaughter time and carcass endpoint (Bautista-Díaz et al., 2017; 2020; Sabbioni et al., 2020).
Some researchers (Chay-Canul et al., 2019b; Canul-Solis et al., 2020) have evaluated the use of biometric measurements (BMs) as a practical and inexpensive alternative method that allows small producers to estimate the LW of Pelibuey sheep. This method implies developing mathematical equations from BMs, which are taken directly from the animals, such as heart circumference or girth (HG), hip-width (HW), body length (BL), and height at the withers (WH) (Gurgel et al., 2021). Other studies (Kumar et al., 2018; Chay-Canul et al., 2019a; Sabbioni et al., 2020) have shown that HG presents the greatest correlation with LW in adult sheep. HG has certain advantages over other BMs, such as greater ease of measurement during routine handling because no special facilities are required and it entails less handling of the animal (Villiers et al., 2009). Since correlation between LW and HG varies according to body conformation and condition, age, and physiological state (Franco et al., 2017; Heinrichs et al., 2017), the method needs to be evaluated in each biotype and stage of development.
To the best of our knowledge, no study has evaluated the linear relationship between HG and LW in growing Pelibuey sheep. In this regard, we tested the hypothesis that HG can be used in simple linear equations as the only predictor of LW in such sheep. Therefore, the objectives of the present study were to develop equations to predict LW using HG in growing Pelibuey lambs and to evaluate the adequacy of those predictive models.
Materials and methods
Ethical considerations
The animals were treated in accordance with the guidelines and regulations for animal experimentation of División Académica de Ciencias Agropecuarias, Universidad Juárez Autónoma de Tabasco (approval code: UJAT-DACA-2015-IA-02). The study is reported in accordance with ARRIVE guidelines (Sert et al., 2020).
Animals, diets, and handling
The experiment was conducted at Centro de Integracion Ovina del Sureste (CIOS), located at 17° 78" N, 92° 96" W, in the town of Alvarado Santa Irene, Second Section, state of Tabasco, Mexico. The regional climate is warm-humid, with average minimum and maximum temperatures of 18.5 and 36 °C, respectively, and 2,299.5 mm annual precipitation.
To develop the model, LW and HG of 415 male Pelibuey lambs ranging from 2 months to 1 year in age were recorded. All the animals were clinically healthy, with LW = 25.96 ± 10.25 kg, and HG = 68.31 ± 10.53 cm. The LW of each animal was determined using a digital balance (EQB model, Torrey, Mexico). The HG was measured as the smallest circumference just behind the forelegs in the vertical plane using a flexible fiberglass tape measure (Truper®, San Lorenzo, Mexico) as described by Chay-Canul et al. (2019a). An independent dataset was used to evaluate the adequacy of the models comprising measurements from 84 male Pelibuey lambs with similar characteristics (LW = 20.50 ± 11.25 kg, and HG = 60.45 ± 12.60 cm). The LW and HG were recorded only once in each animal. All animals were kept in raised-slatted floor cages with group-feeding system. The experimental diet was a total mixed feed (80:20 concentrate to forage ratio) containing ground corn, soybean meal, star grass hay, vitamin and mineral premix. Crude protein of the diet was 15% (dry basis) and 12 MJ metabolizable energy.
Three mathematical models were evaluated to predict lamb weight based on HG, namely:
Eq. 1) First-degree equation (linear): LW (kg) = A + B × HG;
Eq. 2) Second-degree equation (quadratic): LW (kg) = A + B × HG + C × HG2; and
Eq. 3) Exponential model: LW (kg) = A × HGB,
where LW = live weight of the lamb (kg); HG = heart girth (cm); "A", "B" and "C" = model parameters.
Statistical analysis
Statistical analyses were performed using SAS software, version 9.0 (SAS Inst. Inc., Cary, NC; 2022). Descriptive statistics were obtained with PROC MEANS, while PROC REG was used to estimate the parameters of linear equations (Eq. 1 and Eq. 2). The modified Gauss-Newton method was used to estimate the parameters of the exponential equation (Eq. 3) employing the SAS software version 9.0, NLIN procedure (SAS Inst. Inc., Cary, NC; 2022). The maximum number of iterations was 100.
Analysis of residuals was included to identify atypical data. These were detected by plotting the studentized residuals against the values predicted by the equation and eliminated if the value of the studentized residuals was outside the range of −2.5 to 2.5. The goodness-of-fit of the regression models was evaluated using the Akaike information criterion (AIC), Bayesian information criteria (BIC), the coefficient of determination (r2), the mean square error (MSE), and the root MSE (RMSE).
Statistical analyses for model adequacy
Regression analysis was performed from the predicted and observed values (Y = β0 + β1 × X, where Y is the observed value; β0 and β1 represent the intercept and slope of the regression equation, respectively, and X is the value predicted by the equations) to evaluate the performance of the model using the methods suggested by Tedeschi (2006). The F test for the identity of the parameters (β0 = 0 and β1 = 1) of the regression of the data predicted by the observed coefficient of determination (r2), root mean square error (RMSE), standard deviation (SD), mean square error of prediction (MSEP) and root of MSEP (RMSEP) were calculated to assess the accuracy of the values predicted by the model in relation to the observed values. Mean bias (MB) was used to assess model accuracy. The bias correction factor (Cb), a component of the CCC, was used as an indicator of deviation from the identity line. Reproducibility index was calculated and designated as the CCC according to Tedeschi (2006). This was used to simultaneously evaluate the precision and accuracy of the model.
High accuracy and precision were assumed when the coefficients were >0.80, and low accuracy and precision when coefficients were <0.50. The model efficiency statistic (MEF) was used as an indicator of goodness-of-fit. A value of 1 indicates a perfect fit, while values predicted by the model are more variable than the observed values if the MEF value is less than zero. Finally, a coefficient of model determination (CD) was established where a ratio <1 suggests overestimation of the total variance observed in the model-predicted values, and a value >1 suggests underestimation of the total variance by the predicted values. All calculations were performed using the model evaluation system described by Tedeschi (2006).
Results
In the lambs used to develop the model, LW ranged from 6.08 to 49.00 kg, and HG from 43.00 to 88.00 cm. In the lambs used to evaluate the adequacy of the model, LW ranged from 4.45 to 47.75 kg, and HG from 41.50 to 87.00 cm (Table 1). The correlation coefficient between LW and HW was r=0.94. Both fitted regression equations showed high predictive capacity. In addition, all parameters of the equations were significant (Table 2).
Table 1 Descriptive analyses of LW (kg) and HG (cm) in growing male Pelibuey lambs database were used in this study.
| Variables | N | Mean ± SD | Minimum | Maximum |
|---|---|---|---|---|
| Development | ||||
| LW (kg) | 415 | 25.96 ± 10.25 | 6.08 | 49.00 |
| HG (cm) | 415 | 68.31 ± 10.53 | 43.00 | 88.00 |
| Evaluation | ||||
| LW (kg) | 84 | 20.50 ± 11.25 | 4.45 | 47.75 |
| HG (cm) | 84 | 60.45 ± 12.60 | 41.50 | 87.00 |
LW: live weight; HG: heart girt; N: number of observations; SD: standard deviation.
Table 2 Equations for predicting LW in growing male Pelibuey lambs using HG and their adjustment evaluations.
| No. | Equations | N | r2 | RMSE | AIC | BIC | p-Value |
|---|---|---|---|---|---|---|---|
| 1 | LW (kg): −37.70 (± 0.96***) + 0.93 (± 0.01***) × HG | 415 | 0.92 | 2.97 | 906.95 | 915.00 | <0.0001 |
| 2 | LW (kg): −1.74 (± 5.21*) + 0.19 (± 0.16*) × HG+ 0.008(± 0.0001***) × HG2 | 415 | 0.92 | 2.81 | 862.22 | 874.30 | <0.0001 |
| 3 | LW (kg): 0.003 (± 0.0006***) × HG2.68 (±0.04***) | 415 | 0.92 | 2.84 | 868.82 | 876.87 | <0.0001 |
LW: live weight; HG: heart girth; N: number of observations; r2: coefficient of determination; RMSE: root mean square error; AIC: Akaike information criterion; BIC: Bayesian information criterion. Values in parentheses are the standard errors (SEs) of the parameter estimates. *: p<0.05; **: p<0.01; ***: p<0.001.
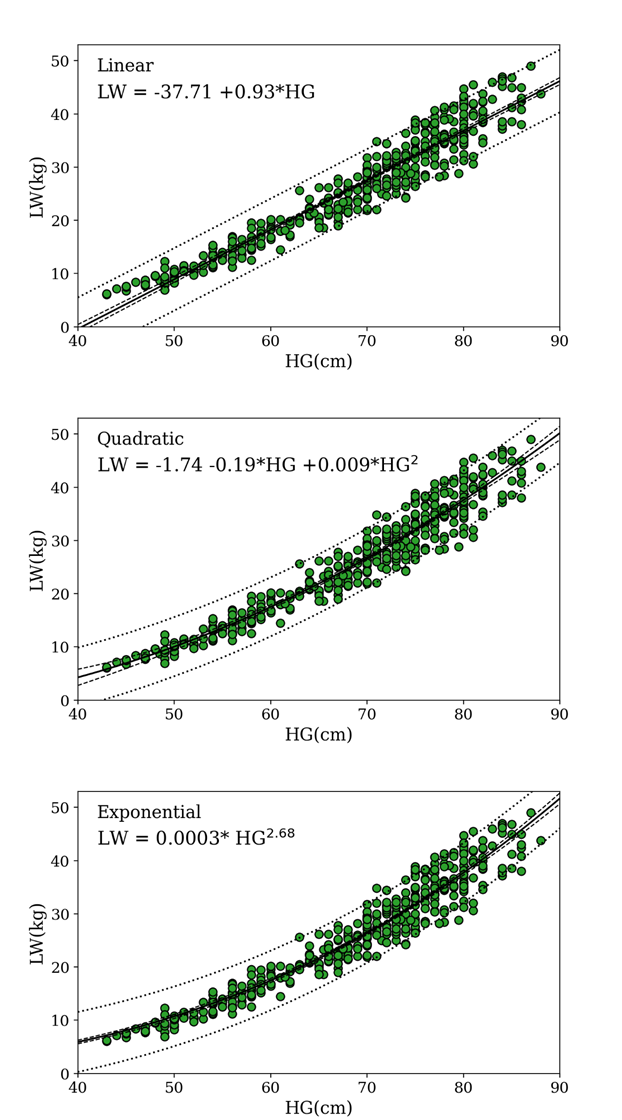
Figure 1 Relationships and fitted equations between LW and HG in growing male Pelibuey lambs: data from 415 animals belonging to the CIOS herd. The solid line represents the trend line of the data. The dotted lines delineate the confidence intervals.
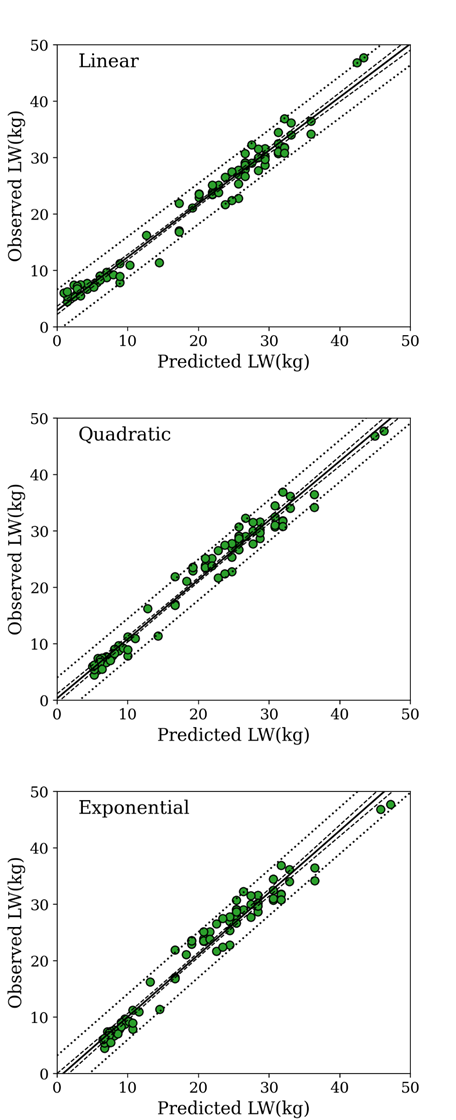
Model adequacy
All models (Eq. 1 to Eq. 3) presented high precision (r2>0.97) and high accuracy (bias correction factor ≥0.98; Table 3), confirming their reproducibility index and concordance with the observed data (CCC≥0.97). The MEF indicated high efficiency of prediction, with a high proportion of the total variance in the observed values being explained by the predicted data (MEF≥0.94: Table 3, Figure 2). The CD ranged from 0.89 to 1.23, indicating high variability of the predicted data (Table 3). In Eq. 2, the random error was the main component of the MSEP partition (89.96%), while about 9.27% was associated with MB. However, in Eqs. 1 and 3, the MSEP partition showed a considerable proportion of the error attributed to mean and systematic bias, affecting the prediction. However, the parameter identity test (intercept =0; slope =1) was accepted only for Eq. 2 (p>0.05). On the other hand, for Eqs. 1 and 3, the intercept was different from zero and the slope was different from one (p<0.05, Table 3; Figure 2).
Table 3 Mean, descriptive statistics and accuracy and precision analysis of the equations used to describe the relationship between LW and HG in growing male Pelibuey lambs.
| Variable | Obs1 | Linear | Quadratic | Exponential |
| Mean | 20.50 | 18.51 | 21.08 | 19.55 |
| SD | 11.25 | 11.71 | 11.27 | 10.08 |
| Maximum | 47.75 | 43.20 | 49.85 | 47.32 |
| Minimum | 4.45 | 0.88 | 5.88 | 6.51 |
| r2 | --- | 0.97 | 0.97 | 0.97 |
| CCC | --- | 0.97 | 0.98 | 0.97 |
| Cb | --- | 0.98 | 0.99 | 0.99 |
| MEF | 0.94 | 0.97 | 0.95 | |
| CD | 0.89 | 0.99 | 1.23 | |
| Regression analysis | ||||
| Intercept (β0) | ||||
| Estimate | --- | 2.96 | -0.26 | -0.96 |
| SE | --- | 0.37 | 0.41 | 0.48 |
| P-value (β0 = 0) | --- | 0.001 | 0.53 | 0.04 |
| Slope (β1) | ||||
| Estimate | --- | 0.94 | 0.98 | 1.09 |
| SE | --- | 0.02 | 0.01 | 0.02 |
| P-value (β1 = 1) | --- | 0.002 | 0.40 | 0.001 |
| MSEP source, % MSEP | ||||
| Mean bias | --- | 52.63 | 9.27 | 15.53 |
| Systematic bias | --- | 4.90 | 0.76 | 16.47 |
| Random error | --- | 42.46 | 89.96 | 67.98 |
| Root MSEP | ||||
| Estimate | --- | 2.74 | 1.87 | 2.41 |
| % of the mean | --- | 13.39 | 9.17 | 11.44 |
SD: standard deviation; r2; coefficient of determination; Cb: bias correction factor; CCC: concordance correlation coefficient; MEF: modeling efficiency statistic; CD: coefficient of model determination; SE: standard error; MSEP: mean square error of the prediction. Obs1: Observed values of the evaluation data set.
Discussion
The positive (r=0.94) and significant (p<0.001) linear correlation found between LW and HG in this study supports the opportunity of using this biometric parameter to predict body weight of growing Pelibuey lambs reared under field conditions, in the absence of scales. Likewise, several researchers have reported high correlation coefficients (r= ≥0.75) between LW and HG in different sheep (Afolayan et al., 2006; Mavule et al., 2013; Mahmud et al., 2014; Chay-Canul et al., 2019a; Kandoussi et al., 2021) and goat breeds (Villiers et al., 2009) kept under farm conditions. It is important to note that some of these researchers found that fit or adequacy, precision, and amount of variability explained by the fitted model (r2) improved considerably when other biometric parameters were included in the model, such as HW, BL and withers height. However, simple models can be used more easily in practice in extensive sheep rearing, as they require the measurement of fewer parameters in the herd (Sabbioni et al., 2020). This is important because while in intensive sheep farms, LW measurement is performed daily due to advanced management and availability of basic measurement equipment, this task is more complex in extensive farms, especially under free field-conditions (Sabbioni et al., 2020).
The HG has been the biometric parameter most used to predict LW of farm animals. It has been used in heifers (Oliveira et al., 2013), goats, and sheep (Conrado et al., 2015; Chay-Canul et al., 2019). Furthermore, several authors indicate that HG is highly correlated with LW for different animal species (Yilmaz et al., 2013; Chay-Canul et al., 2019a). Malková et al. (2021) estimated LW by HG in purebred Charollais, and Kent and crossbred sheep. They reported that r2 was 0.75. Moreover, Kumar et al. (2018) also reported that HG can estimate LW of Harnali sheep with high precision (r2 = 0.87). Likewise, under experimental conditions, Bautista-Díaz et al. (2017) found that HG was the best predictor of LW in Pelibuey ewes compared to other biometric parameters (r2=0.72).
In the present study, the second-degree equation (Eq .2) provided a better fit than the linear first-degree and exponential equations because of its lowest RMSE, AIC, and BIC values (Table 2). In turn, Canul-Solis et al. (2020) compared different mathematical equations to predict LW using HW in Pelibuey sheep and determined that the linear model (LW (kg) = − 19.17 + 3.46 × HW) performed the best according to the goodness-of-fit evaluation: P<0.0001, r2 = 0.96; AIC= 3,342.0; BIC= 3,355.1; Sxy= 0.94. Salazar-Cuytun et al. (2021) compared three equations (linear, quadratic and exponential) to evaluate the relationship between body volume and weight of Pelibuey lambs and ewes. They observed that the quadratic model had the best performance according to the adequacy assessment.
Model adequacy
Precision and accuracy parameters showed that the proposed equations had high precision (r2 >0.95%), accuracy (Cb >0.98), and reproducibility (CCC >0.96) for predicting LW of lambs and adult ewes. The model efficiency (MEF ≥0.93) indicated a relatively high concordance between observed and predicted values, considering that a perfect fit is equal to 1. In this case, a CD value >1 indicates underprediction and a CD value <1 indicates overprediction (perfect fit =1) (Tedeschi, 2006). In Eq. 2, a small proportion of the prediction error was associated with the slope, although most of the error was explained by the random component, which indicated small prediction bias. Based on the results of these statistical evaluations, Eq. 2 predicted the observed LW with good precision and accuracy. It accounted for over 90% of the LW variation.
The results of the present study can contribute to estimate body weight in growing Pelibuey sheep and also to the updating of data for the estimation of LW and other parameters required by current nutritional models to predict productive behavior of hair sheep (Chay-Canul et al., 2016; 2019b).
In the present study, the second-degree equation predicted live weight with high accuracy and precision. Moreover it showed the best performance according to the goodness-of-fit evaluation and external validation. Hence, this model is proposed for determining live weight of Pelibuey sheep using HG as the sole predictor variable.