Introducción
La madera obtenida de plantaciones de Eucalyptus sp. es un recurso fundamental por la serie de servicios socioeconómicos que proporciona en la fabricación de muebles, papel y generación de energía, lo cual ha estimulado su producción masiva de forma económicamente sustentable con el manejo forestal eficiente de plantaciones, lo que exige el monitoreo permanente de los volúmenes de madera producidos.
La estimación de la cantidad de madera disponible o producida en plantaciones forestales se realiza típicamente a través de ecuaciones alométricas utilizando medidas de los árboles obtenidas en campo con personal entrenado y materiales y equipamientos especializados, una labor difícil de hacer en extensas áreas, teniendo como factor condicionante la inversión monetaria y el tiempo (Maltamo et al., 2015).
El desarrollo del conocimiento humano ha conducido a la integración de tecnologías en las actividades involucradas en los sistemas de producción, elevando su competitividad en el mercado y reduciendo varias actividades que antes se realizaban de forma manual. En este sentido, las imágenes digitales obtenidas por satélite con percepción remota son tecnologías útiles para la obtención de informaciones de las coberturas terrestres, reduciendo acciones de campo que pueden llevar a errores procedimentales (Lu et al., 2016; Pitriya et al., 2018). Componentes de las imágenes como las bandas espectrales y derivadas de características texturales e índices de vegetación, pueden ser usados como variables para la modelación espacial de la dendrometría forestal (Lu et al., 2016). Los índices de vegetación maximizan la caracterización forestal y minimizan la influencia de efectos generados por el suelo, los ángulos de iluminación y las condiciones atmosféricas (Sarker y Nichol, 2011). Por su parte, la textura permite maximizar las diferencias entre el dosel de los árboles, reducir los factores de sombra inducidos por la altura entre las plantas y los efectos causados por la topografía (Pham y Brabyn, 2017).
Estimar la volumetría de bosques con información derivada de imágenes representa un trabajo complejo, no obstante métodos como las redes neurales artificiales (ANNs, su sigla en inglés) son herramientas de procesamiento de datos que permiten establecer predicciones a partir de reconocimientos de padrones entre variables (Zhu et al., 2015; Ghosh y Behera, 2018).
Existen investigaciones (Foody et al., 2001; Zhu et al., 2015; Lu et al., 2016) que utilizan la aplicación de ANN para la estimación de la biomasa en plantaciones forestales, usando bandas espectrales e índices de vegetación (sin considerar las texturas) provenientes de satélites Landsat TM y Worldview-2, y permiten concluir que las imágenes digitales tienen un alto potencial para hacer estimaciones en plantaciones forestales en escala regional a través de redes neuronales.
Igualmente se han desarrollado investigaciones que permiten estimar la cantidad de biomasa en bosques nativos y cultivados, basados en métodos de regresión linear y técnicas automatizadas de aprendizaje de máquinas (Lu et al., 2016; Ghosh y Behera, 2018). Entre los modelos de aprendizaje empleados se encuentran el algoritmo de Floresta aleatoria, Estocástico de mejoramiento de gradiente, Máquina de vector de soporte y K-vecino más próximo, desarrollados por Ghosh y Behera (2018) usando imágenes Sentinel, López-Serrano et al (2016) con Landsat 5 y por Pham y Brabyn (2017)) con SPOT 4 y 5, con los cuales se demostró que los índices de vegetación son variables más precisas para la predicción de biomasa que las texturas obtenidas con Matriz de coocurrencia de niveles de grises (GLCM), demostrando también que conjuntamente las texturas y los índices tienen una mayor precisión que cuando se utilizan de manera individual. Resultados similares se encontraron con los modelos de regresión propuestos por Sarker y Nichol (2011) y Zhang et al. (2015), respectivamente, con imágenes digitales de satélite ALOS y GaoFen-1.
Actualmente no se conocen procedimientos para mapear el volumen de madera en poblaciones forestales utilizando bandas espectrales e índice de vegetación, conjuntamente con características texturales por medio de ANN, y aun es necesario evaluar su potencial de uso (Lu et al., 2016; Ghosh y Behera, 2018). Por esta razón, la presente investigación tuvo como objetivo desarrollar un modelo de ANNs para estimar la distribución espacial del volumen de madera en plantaciones de eucalipto (Eucalyptus sp.) empleando informaciones de bandas espectrales, textura e índices de vegetación provenientes de imágenes digitales de satélite Spot 6.
Materiales y métodos
Área de estudio, datos de campo e imagen de satélite
El área de estudio consistió en una plantación de eucalipto de 9431.21 ha, localizada en el estado de Mato Grosso del Sur, en la región Centro-oeste de Brasil, con relieve plano y algunos resaltos topográficos de declividad suave.
Se utilizaron datos de volumen de madera sin cascara (m3/ha) de 210 parcelas circulares de 500 m2 cada una (Figura 1), distribuidas de forma sistemática en la plantación, que fueron determinadas con ajuste por clase de edad del modelo polinómico de quinto grado de Schopfer, basado en medidas de diámetro a la altura del pecho (1.3 m) y altura total del conjunto de plantas parceladas, además de la cubicación de algunos árboles (Favalessa et al., 2012). Esta información se adoptó como variable deseada para el aprendizaje y validación de las redes neurales.
Se utilizó una imagen digital Spot 6, que representa espacialmente el área de estudio, con bandas espectrales del azul (Banda 1), verde (Banda 2), rojo (Banda 3) e infrarrojo próximo (Banda 4), con resoluciones espaciales de 1.5 m por estar combinadas con la banda pancromática de la misma imagen. La imagen no presenta ruidos por errores instrumentales del sensor receptor y una mínima interferencia atmosférica ya que es una captura en condiciones de cielo despejado. Las bandas se redimensionaron a 8 bits y fueron corregidas por efectos atmosféricos con datos de calibración registrados por el satélite, procesos desarrollados a través del programa Qgis 2.18.5. De las bandas se derivaron las texturas e índices de vegetación, siendo estos tres componentes, además de la respectiva edad de la plantación, las variables de predicción o de entrada a las ANNs. Las informaciones de campo y de percepción remota corresponden para el mismo período de agosto de 2015.
Las 210 parcelas muestreadas con las respectivas variables de entradas y salidas deseadas asociadas, fueron distribuidas en dos grupos, uno de 126 (60%) y otro de 84 (40%) unidades, designados respectivamente para el aprendizaje y la evaluación de las redes.
Cálculo de texturas de bandas espectrales e índices de vegetación
Para cada banda espectral se determinaron de manera cuantitativa nueve tipos de texturas, consistentes en: Segundo Momento Angular (ASM), Momento inverso de diferencia (IDM), Contraste (CON), Correlación (COR), Entropía (ENT), Variancia (VAR), Media de la Suma (SA), Variancia de la Suma (SV) y Suma de la entropía (SE). Además la textura obtenida por medio GLMC, derivada de sesiones de 3 x 3 pixeles, con la cual se calculó la ocurrencia de valores vecinos para todas las direcciones (0o, 45o, 90o y 135o), relacionando los elementos p(i,j) posicionados en las i filas y j columnas de la GLCM, aplicando las ecuaciones estadísticas que aparecen en la Tabla 1 (Sarker y Nichol, 2011; Lofstedt et al., 2019).
Tabla 1 Ecuaciones para el cálculo de manera cuantitativa de los tipos de textura3.

a. Segundo Momento Angular (ASM), Momento inverso de diferencia (IDM), Contraste (CON), Correlación (COR), Entropía (ENT), Variancia (VAR), Media de la Suma (SA), Variancia de la Suma (SV) y Suma de la entropía (SE). N = número total de columnas y filas de la GLCM, definido según la variación de grises de la imagen. Los símbolos μx, μy y σx, σy corresponden a los valores medios y desviación padrón de las filas y columnas de la GLCM, respectivamente; px+y(k) es la suma de la distribución de los valores de los pixeles () con k=i+j. Estas texturas fueron calculadas usando el comando r. texture del software Grass GIS 7.0.5.
Los índices adoptados (Tabla 2) se encuentran entre los más utilizados, siendo estos: Índice de vegetación por la razón (RVI), Índice de vegetación por la diferencia (DVI), Índice de vegetación por diferencia normalizada (NDVI), Índice de vegetación por diferencia normalizada verde (GNDVI), Índice de vegetación por resistente a la atmosfera (ARVI), Índice de vegetación mejorado (EVI) y Índice de vegetación Ajustado al Suelo (savi).
Tabla 2 Índices de vegetación utilizados en el estudio.

γ = factor de autocorrección atmosférica, que normalmente se define con valor de 1 (Alba et al., 2017). L es un factor de corrección que minimiza el efecto de reflectancia del suelo, estimado como 0.25 para áreas de bosque (Ren et al., 2018). C1 y C2 son coeficientes de corrección atmosférica, definido comúnmente con valores de 7 y 6, y G es un factor establecido con valor constante de 2.5 (Situmorang et al., 2016). El procesamiento aritmético para el cálculo de los índices fue realizado en el software Qgis 2.18.5.
El índice RVI fue determinado por la división de la banda 4 (B4) entre banda 3 (B3) de la imagen digital Spot 6 (Ecuación (10)) (WANG et al., 2012). El DVI, definido por la ecuación (11), resultó de la sustracción de la banda 4 con la 3; el NDVI se obtuvo por la división entre la diferencia de la banda 4 con la 3 y la suma de las mismas, según la ecuación (12), y el GNDVI fue calculado con igual ecuación matemática que el NDVI, pero cambiando la banda 3 por la 2 (B2), como está en la ecuación (13) (Alba et al., 2017). El ARVI integra las bandas 4, 3 y 1 (B1), como se observa en la ecuación (14) (Pitriya et al., 2018). El SAVI fue calculado con las bandas 4 y 3, de acuerdo con la Ecuación (15) (Ren et al., 2018). El EVI, definido con la Ecuación (16), se construyó con los pixeles de las bandas 4, 3 y 1 (Situmorang et al., 2016).
Arquitectura, aprendizaje y validación de las ANNs
Para el diseño de las ANNs se definió una estructura neuronal de perceptron multicapa con dos capas ocultas y una de salida, flujo de alimentación hacia adelante e interconexiones totales acíclicas entre las neuronas, una configuración capaz de resolver tareas complejas (Haykin, 2009; Hagan et al., 2014). En la capa de salida fue establecida una neurona que produciría la estimación de la red. Para la primera y segunda capa oculta fueron evaluadas diferentes combinaciones posibles, considerando entre 1 y 30 neuronas, para un total posible de 900 redes estructuras, entrenadas y evaluadas.
Las ANNs fueron modeladas por medio del Algoritmo de propagación de error, típicamente utilizado por su alta eficiencia de aprendizaje, una vez definida la función sigmoide logística para el procesamiento de información en las neuronas y establecido un valor fijo de entrada junto con las variables, denominada bias, con el fin de evitar que los valores de las entradas fueran nulos entre sí (Haykin, 2009; Hagan et al., 2014).
Considerando que la eficiencia del proceso de aprendizaje de las ANNs está sujeto al número de variables introducidas y la correlación de éstas con la estimada (Hagan et al., 2014); en el estudio, específicamente de las nueve bandas, siete índices y nueve texturas, se seleccionaron para el aprendizaje aquellas de mayor correlación con el volumen de madera por parcela muestreada, utilizando el método de Spearman que permite evaluar tanto relaciones lineales como no lineales.
El proceso de construcción y aprendizaje de las ANNs se efectuó usando el comando neuralnet del software R 3.5.1, con 126 unidades ‘amuéstrales’. Las variables de entrada correspondientes al resto de muestras (86 parcelas) no empleadas en el aprendizaje fueron procesadas por las redes utilizando el comando compute de R 3.5.1 y las respuestas estimadas fueron evaluadas con el volumen correspondiente obtenido con las medidas de campo mediante la raíz de error medio cuadrático (RMSE), coeficiente de correlación de Pearson (r) y precisión de las estimaciones. La ANN resultante con mejor desempeño fue integrada al programa Qgis 2.18.5, al mismo tiempo que fueron introducidas las variables respectivas de toda la extensión de la plantación antes de ser geoprocesadas en la elaboración del mapa temático de volumen de madera por pixel.
Resultados
Variables de entrada a la ANN
Como información de entrada a las ANNs fueron seleccionadas las variables presentadas en la matriz de correlación de la Figura 2. Estas variables presentaron relaciones significativas con el volumen promedio de madera por parcelas, con valores absolutos próximos y mayores que 0.6. En la Figura 2 se observa que las bandas B1, B2 y B3 presentaron, respectivamente, coeficientes de correlación de -0.765, -0.775 y -0.751 con respecto al volumen, con relaciones exponenciales estrictamente decrecientes, o sea, en la medida que disminuyen los valores espectrales inversamente aumenta la cantidad de madera. Por otra parte, la banda B4 presentó un coeficiente de -0.128, sin una tendencia de relación definida. De la misma manera, con distribución exponencial estrictamente decreciente con referencia al volumen, las texturas SA derivada de la banda 1 (SA_B1), SA de la 2 (SA_B2), SA de la 3 (SA_B3) y SV de la 1 (SV_B1) presentaron, respectivamente, correlaciones de -0.661, -0.603, -0.591 y -0.596. Los demás tipos de texturas presentaron coeficientes con valores absolutos menores que 0.51 y no se relacionaron claramente con la volumetría. El GNDVI fue el índice que mejor se correlacionó con el volumen, con un coeficiente de 0.550, de forma exponencial creciente. Además, la edad de los árboles fue la variable de mayor correlación (0.840) con tendencia lineal directamente proporcional.
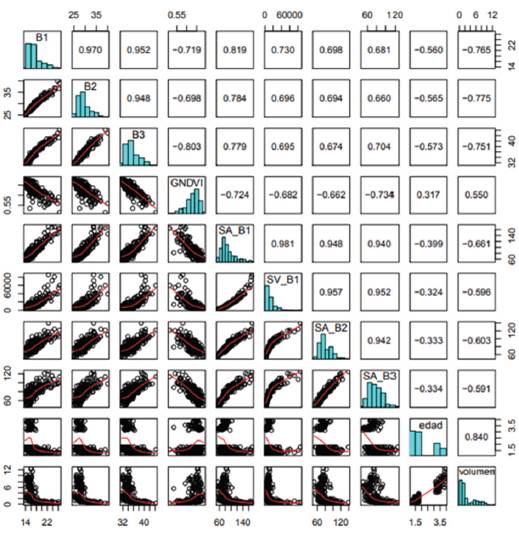
Figura 2 Correlación del volumen de madera de eucalipto con las bandas 1 (B1), 2 (B2) e 3 (B3); Índice de vegetación por diferencia normalizada verde (GNDVI); las texturas Media de la Suma derivada de la banda 1 (SA_B1), 2 (SA_B2) e 3 (SA_B3); la textura Variancia de la Suma derivada de la banda 1 (SV_B1); y la edad de la floresta.
Modelo y evaluación de la ANN
Entre las redes estructuradas, el mejor desempeño se obtuvo con la ANN formada por 11 neuronas en la primera capa oculta, 20 en la segunda y la respectiva neurona en la capa de salida (Figura 3), con RMSE de 7.85 m3/ha, que representa una inexactitud o diferencia de 16.45% (RMSE relativo) entre los valores del conjunto de volúmenes estimados respecto a los determinados con mediciones en campo.

Figura 3 Representación estructural de la mejor ANN (11-20-1). Variables de entrada (verde), neuronas ocultas (rojo), bias (azul) y neurona de salida (café).
El coeficiente de Pearson resultante fue de r = 0.988 y el coeficiente de determinación de r2 = 0.9761 con una precisión de 93.32%, lo que significa un alto grado de linealidad y concordancia de cada una de las predicciones con los volúmenes esperados (Figura 4).

Figura 4 Volumen estimado con la ANN vs. volumen de madera de eucalipto calculado por inventario con mediciones de campo.
El gráfico de dispersión de los errores residuales de las estimaciones (Figura (5a)) muestra las discrepancias porcentuales para cada parcela. Es evidente que la mayoría de los residuos se concentra entre 0 y ±20%, con varianza homogénea. En la Figura 5(b) se observa el gráfico cuantil-cuantil (Q-Q plots) de los residuos, con alineamientos aproximados de los puntos, demostrando que los residuos siguen una distribución normal. Esto permite corroborar que las variabilidades de las estimaciones presentan error con tendencia central alrededor de cero, lo que destaca a la ANN como modelo no tendencioso en la sobreestimación o subestimación del volumen de madera de eucalipto en estudio. Por tanto, la ANN tiene capacidad para realizar estimaciones del volumen forestal con valores de baja discrepancia en relación con los determinados por medidas de campo, dependiendo del error previsto de las estimaciones.

Figura 5 Gráficos de dispersión de los residuos (a) y cuantil-cuantil Q-Q (b) de volúmenes estimados de madera de eucalipto
Ghosh y Behera (2018) estimaron la cantidad de biomasa (Megagramo por hectárea (Mg/ha) en bosque tropical en la India, utilizando índices de vegetación y texturas derivados de las bandas espectrales de la imagen Sentinel, desarrollaron un modelo con algoritmo estocástico de mejoramiento de gradiente con coeficiente de determinación de 0.73 (RMSE de 121.79 Mg/ha) y otro con algoritmo de floresta aleatoria con 0.74 (RMSE de 73.49 Mg/ha). Del mismo modo, Pham y Brabyn (2017) con algoritmo de floresta aleatoria, utilizando bandas espectrales derivadas de texturas e índices de vegetación de imágenes SPOT 4 y 5, mapearon la biomasa de manglares en Vietnam, consiguiendo estimativos con coeficiente de determinación de 0.73 y precisión de 77.1%, que corresponde a RMSE de 78.2 Mg/ha. con variables similares, pero a partir de la imagen Landsat 5 y utilizando diferentes técnicas de aprendizaje (Algoritmo de Floresta aleatoria, Máquina de vector de suporte y K-vecino más próximo), López-serrano et al. (2016) desarrollaron predicciones de la cantidad de biomasa en plantaciones de pinos y robles en México, encontrando la mejor eficiencia con el algoritmo K-vecino con coeficiente de determinación de 0.66 (RMSE de 26.64 Mg/ha). Estas predicciones de parámetros de los árboles son claramente menos eficientes que las resultantes en la presente investigación con la red neuronal.
Zhang et al. (2015) en China desarrollaron modelos de regresión lineal usando bandas espectrales, índices de vegetación y texturales, a través de imágenes del satélite GaoFen-1 para medir la biomasa en bosques de Populus Euphratica, con una precisión de 91.54% y una RMSE de 25.22 Mg/ha. En Hong-Kong, Sarker y Nichol (2011) utilizando bandas espectrales del sensor AVNIR-2, índices de vegetación y textura, estimaron la biomasa del bosque subtropical con una variabilidad de datos de campo de 88% y un RMSE de 32 Mg/ha.
Zhu et al. (2015) utilizaron ANN multicapa con bandas espectrales e índices de vegetación como variables de entrada en el mapeo de la biomasa de 700 ha de manglar en la China con imagen del satélite Worldview-2, encontraron predicciones con RMSE relativo de 18.17% (24.32 Mg/ha). Foody et al. (2001) en bosques tropicales en Malasia, con imagen Landsat TM calcularon coeficiente de correlación de 0.8 entre los valores calculados por ANN y los determinados a través de ecuaciones alométricas.
Mapa de volumen de madera del bosque forestal
El modelo de la ANN aplicado para el área total de la plantación resultó en la distribución espacial del volumen de madera que aparece en el mapa temático de la figura 6.
Como se puede observar, el volumen de madera varía entre 0 - 40 m3/ha (color rojo) hasta las mayores cantidades (201 -250 m3/ha -color negro). En este mapa quedan referenciadas las zonas con altas y bajas cantidades de madera dentro de la plantación, lo que se puede usar como soporte para el manejo forestal.
En el histograma de frecuencias de la Figura 7 se observan los volúmenes de madera por pixeles que se presentan en el mapa de la Figura 6. La mayor frecuencia ocurre entre 50 a 80 m3/ha y entre 150 y 180 m3/ha.
Discusión
En la medida en que disminuyen los niveles digitales en los pixeles de las bandas correspondientes a las longitudes de onda azul, verde y rojo del espectro electromagnético (B1, B2 y B3, respectivamente) aumenta el volumen de madera. Esto es debido a que tales espectros de radiaciones son absorbidas en diferentes proporciones por la vegetación según los procesos biológicos, así, los árboles de mayor porte presentan la absorción más alta y consecuentemente las reflectancia menores registradas en los pixeles de las bandas; por el contrario, el espectro infrarrojo (B4) es muy poco absorbido por la clorofila y es reflectado con la misma intensidad por los árboles, independiente de su porte (Aquino y Oliveira, 2012; Chuvieco, 2016).
Con el uso de la ecuaciones de las texturas SA y SV fue posible identificar la variación de la volumetría de la madera, ya que los valores de los niveles digitales de cada pixel generado por éstas varían según la absorción y reflectancia de la radiación de acuerdo con el porte de los árboles; por el contrario, las demás texturas solo analizan la organización de los pixeles vecinos conforme su organización espacial (Lofstedt et al., 2019).
La ANN construida es útil para predecir el volumen de madera de la vegetación forestal sin predicciones tendenciosas, siendo adecuada en áreas de bosque donde el trabajo de campo resulta difícil de realizar.
Cuando se compara con otros métodos de aprendizaje, utilizando las mismas variables, la ANN resulta más exacta y precisa para la estimación del volumen de madera, por tanto, los modelos basados en neuronas son mecanismos más eficientes en la predicción de parámetro del bosque con informaciones remotas. Cuando se comparan con métodos de regresiones lineales, el desempeño de las ANN puede ser inferior, pero asumir una relación lineal' es una suposición que no tiene en cuenta dependencias no lineales complejas que las ANNs pueden subentender y no configurar en modelos de estimación tendenciosos (Chen et al., 2016; López-Serrano et al., 2016; Pham y Brabyn, 2017). Con respecto a otras ANNs que utilizan solamente bandas espectrales e índices de vegetación, el desempeño de la red construida fue superior, por lo que las texturas utilizadas funcionan como variables que aumentan la eficiencia de las predicciones.
Conclusiones
La ANN construida presentó un error padrón residual de 16.32% (RMSE de 7.85 m3/ha), coeficiente de determinación de 0.976 y precisión de 93.32%. Siendo éste un rendimiento aceptable, ya que los errores residuales de las estimaciones indican un adecuado ajuste, y un modelo sin suposiciones tendenciosas, por tanto, su aplicación es aceptable para mapear la distribución de volúmenes de madera en extensas áreas con las respectivas variables de entradas definidas.
La red propuesta, cuando se compara con otros métodos de aprendizaje, es más eficiente y tiene mejor precisión y exactitud; inclusive que ANNs que utilizan bandas espectrales e índices.
La red neuronal construido en este estudio es una opción para ser aplicada en otras regiones con plantaciones de Eucalyptus sp. No obstante, es necesario hacer más investigaciones para evaluar y perfeccionar su uso y eficiencia en plantaciones tanto cultivadas como naturales de diversas especies, en distintas regiones geográficas del mundo y con diferentes tipos de imágenes de satélites.

















