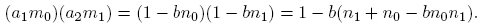1. Introducción

Denotamos por R, Z y N los conjuntos de los números reales, de los números enteros y de los números naturales, respectivamente. Además, N₀ = N∪{0}. También denotamos por P el conjunto de los números primos, y suponemos que P ⊂ N. Dados a, b ∈ Z, en donde al menos uno de ellos es diferente de cero, el símbolo〈a, b〉denota el máximo común divisor de a y b. Para cada a, b ∈ N, consideramos las progresiones aritméticas

y

Para a ∈ N y b ∈ Z, también consideramos las progresiones aritméticas

Notemos que P(a, b) = P_G (a, b) si y sólo si〈a, b〉= 1. Además, M(a) = P(a, a). En 1955 Furstenberg probó en [⁶] que la familia

es base de una topología τ_F en Z. También mostró que el espacio topológico (Z, τ_F ) es segundo numerable y T ₄, por lo que es metrizable. Más aún, hizo ver que cada básico P_F (a, b) es abierto y cerrado en (Z, τ_F ), así que este espacio es cero-dimensional y no conexo.

Tanto en 1959 como en 1962, Golomb probó en [⁷] y en [⁸] que la familia

es base de una topología τ_G en N (ver Teorema 3.2). En [¹², Ejemplos 60 y 61, p. 82], cuya primera edición fue publicada en 1970, a τ_G se lo llama la “topología del entero primo relativo”. En el presente trabajo, al igual que en los artículos [¹³], [¹⁴], [¹⁵], [¹⁶], [¹⁷] y [¹⁸] de Szczuka, a τ_G lo llamamos la topología de Golomb, y decimos que el espacio topológico (N, τ_G ) es el espacio de Golomb.

En [⁷, Teoremas 2 y 3, p. 663] y [⁸, Teoremas 2 y 3, p. 180], Golomb probó que (N, τ_G ) es segundo numerable, T ₂ y conexo (ver Teoremas 4.1, 4.11 y 4.17). Usando el hecho de que, para cada p ∈ P, el conjunto M(p) es cerrado en (N, τ_G ) (ver Teorema 4.2), Golomb probó en [⁷, Teorema 1, p. 663] y [⁸, Teorema 1, p. 180], que P es infinito (ver Teorema 4.3). Usando una fuerte herramienta de la Teoría Analítica de Números, Golomb probó en [⁷, Teoremas 6 y 7, p. 664] y [⁸, Teoremas 6 y 7, p. 181], que P es denso en (N, τ_G ) y tiene interior vacío (ver Teoremas 4.28 y 4.29).

La prueba de la conexidad de (N, τ_G ), como fue presentada por Golomb, utiliza argumentos propios de la Teoría de Números. Como se indica en [⁷, p. 663] y [⁸, p. 180] “una prueba de la conexidad de (N, τ_G ), que no utiliza argumentos de la Teoría de Números, fue presentada por Brown en abril de 1953, durante el congreso de la Sociedad Matemática Americana”, que se llevó a cabo en la ciudad de Nueva York. Brown estudió el espacio (N, τ_G ) antes que Golomb, pero no publicó sus resultados. El resumen de la plática de Brown, publicado en [², p. 367] y en donde se bosqueja la manera de demostrar la conexidad de (N, τ_G ), motivó en 2017 a Clark, Lebowitz-Lockard y Pollack, a acuñar en [³] la siguiente noción.

Definición 1.1. Un espacio de Brown es un espacio topológico X tal que para cada dos subconjuntos abiertos y no vacíos U y V de X, tenemos que cl _X (U) ∩ cl _X (V) ≠ ∅. Si X es un espacio topológico y Y ⊂ X, decimos que Y es un espacio de Brown en X si Y, como subespacio de X, es de Brown.

Sea X un espacio topológico. Para simplificar, diremos que X es de Brown, en lugar de decir que X es un espacio de Brown. Si X es no numerable y su topología es la del complemento finito o bien la del complemento numerable, entonces X es de Brown. El siguiente resultado aparece en [³, Proposición 6].

Teorema 1.2. Todo espacio de Brown X es conexo.

Demostración. Si X no es conexo, entonces existen dos subconjuntos no vacíos U y V de X, abiertos y cerrados en X, tales que X = U ∪ V y U ∩ V = ∅. Entonces cl _X (U) ∩ cl _X (V ) = U ∩ V = ∅, lo cual contradice el hecho de que X es de Brown. ☑

En el presente trabajo damos una prueba explícita del hecho de que (N, τ_G ) es de Brown (ver Teorema 4.17). También probamos que, para cada d ∈ N, la progresión aritmética P_G (1, d) es de Brown en (N, τ_G ) (ver Teorema 4.16).

En 1969 Kirch demostró en [⁹, Teorema 1, p. 169], que (N, τ_G ) no es localmente conexo. Formalmente, hizo ver que (N, τ_G ) no es localmente conexo en 1. Luego de esto definió, en el mismo artículo, una topología τ_K en N tal que τ_K ⊂ τ_G y (N, τ_K ) es conexo, T ₂ y localmente conexo. Aunque Kirch fue el primero en probar que (N, τ_G ) no es localmente conexo, presentamos este hecho de manera más general, pues, como vemos en el Teorema 4.20, para ningún d ∈ N el conjunto P_G (1, d) es conexo en pequeño o casi conexo en pequeño, en cada uno de sus puntos.

El presente trabajo está dividido en cuatro secciones. Luego de esta Introducción, en la Sección 2 presentamos una serie de nociones y resultados, propios de la Teoría de Números y de la Topología General, que serán necesarios para probar las propiedades topológicas del espacio (N, τ_G ), trabajo que se realiza en las Secciones 3 y 4. Conviene destacar que varios resultados presentados en la Sección 4 aparecen por vez primera. Incluimos en la Sección 4 una serie de preguntas abiertas.

2. Definiciones y resultados iniciales

En esta sección presentamos una serie de definiciones y resultados básicos que utilizaremos para probar los enunciados principales. La mayoría de los resultados, propios de la Teoría de Números y de la Topología General, son conocidos y se indica, en cada caso, una referencia adecuada. Un conjunto es numerable si tiene la misma cardinalidad que un subconjunto de N. Un conjunto es infinito numerable si tiene la misma cardinalidad que N.

3. La topología de Golomb

Recordemos que para cada a, b ∈ N con〈a, b〉= 1,

En el siguiente teorema, enlistamos tres propiedades de los conjuntos anteriormente definidos.

Teorema 3.1. Para cada (a, b) ∈ N × N con〈a, b〉= 1, se satisfacen las siguientes propiedades:

Demostración. Para ver 1) y 2), sea (a, b) ∈ N×N con〈a, b〉= 1. Entonces b = a(0)+b ∈ P_G (a, b), es decir, b ∈ P_G (a, b). Para probar la infinitud de P_G (a, b), sea f: N₀ → P_G (a, b) la función definida como f(m) = am+ b, para cada m ∈ N₀. Si n,m ∈ N₀ son tales que f(n) = f(m), entonces an + b = am + b, por lo que an = am y, como a ∈ N, la igualdad am = an implica que n = m. Esto prueba que f es inyectiva. Claramente f es sobreyectiva, así que f es biyectiva. Luego N₀ y P_G (a, b) tienen la misma cardinalidad, de donde P_G (a, b) es infinito numerable. Para ver que P_G (1, 1) = N, sea n ∈ N. Como n = 1(n − 1) + 1 y (n − 1) ∈ N0, se sigue que n ∈ P_G (1, 1). Luego N ⊂ P_G (1, 1). Como también P_G (1, 1) ⊂ N, concluimos que P_G (1, 1) = N. Esto prueba 1).

Para probar 2), sea c ∈ P_G (a, b). Entonces existe n ∈ N₀ tal que c = b + na. Por el Teorema 2.2,〈c, a〉=〈a, b〉= 1. Si y ∈ P_G (a, c), entonces existe n ₁ ∈ N₀ tal que y = c+n ₁ a. Luego

Esto prueba que P_G (a, c) ⊂ P_G (a, b) y 2) se cumple.

Para probar 3), sean b ∈ N y a ₁, a ₂ ∈ N tales que〈b, a ₁〉=〈b, a ₂〉= 1. Por el Teorema 2.4,〈b, a ₁ a ₂〉= 1. Si x ∈ P_G (a ₁ a ₂, b), entonces existe n ∈ N₀ tal que x = b + n(a ₁ a ₂). Por tanto, x = b + (na ₂)a ₁ ∈ P_G (a ₁, b) y x = b + (na ₁)a ₂ ∈ P_G (a ₂, b). Luego x ∈ P_G (a ₁, b) ∩ P_G (a ₂, b). Esto termina la prueba de 3). ☑

Consideremos ahora la familia

Como indicamos en la Introducción, Golomb probó en [⁷] y en [⁸] que B_G es base de la topología τ_G en N que se indica en el siguiente resultado.

Teorema 3.2. La familia

es una topología en N. Además B_G ⊂ τ_G y B_G es una base del espacio topológico (N, τ_G ).

Demostración. Vamos a probar primero que τ_G es una topología. Por definición ∅ ∈ τ_G . Para cada b ∈ N, 1 ∈ N es tal que〈1, b〉= 1 y P_G (1, b) ⊂ N. Por tanto, N ∈ τ_G . Sea {U_i : i ∈ I} una familia de elementos en τ_G . Dada b ∈ ∪ _i∈I U_i , existe i ₀ ∈ I tal que b ∈ U_{i 0} . Como U_{i 0} ∈ τ_G , existe a ∈ N tal que〈a, b〉= 1 y P_G (a, b) ⊂ U_{i 0} . En vista de que U_{i 0} ⊂∪ _i∈I U_i , deducimos que P_G (a, b) ⊂∪ _i∈I U_i . Esto prueba que ∪ _i∈I U_i ∈ τ_G .

Ahora supongamos que U, V ∈ τ_G . Si U ∩ V = ∅, entonces U ∩ V ∈ τ_G . Consideremos, por tanto, que U ∩ V ≠ ∅, y sea b ∈ U ∩ V. Como b ∈ U, existe a ₁ ∈ N tal que〈b, a ₁〉= 1 y P_G (a ₁, b) ⊂ U. Como también b ∈ V, existe a ₂ ∈ N tal que〈b, a ₂〉= 1 y P_G (a ₂, b) ⊂ V. Notemos que a ₁ a ₂ ∈ N. Además, por la propiedad 3) del Teorema 3.1,〈b, a ₁ a ₂〉= 1 y

Esto prueba que U ∩ V ∈ τ_G , por lo que τ_G es una topología en N.

Para mostrar que B_G ⊂ τ_G , sea P_G (a, b) ∈ B_G . Entonces a, b ∈ N y〈a, b〉= 1. Si c ∈ P_G (a, b), por la propiedad 2) del Teorema 3.1,〈a, c〉= 1 y P_G (a, c) ⊂ P_G (a, b). Luego P_G (a, b) ∈ τ_G . Esto prueba que B_G ⊂ τ_G .

Tomemos ahora U ∈ τ_G y b ∈ U. Entonces existe a ∈ N tal que〈a, b〉= 1 y P_G (a, b) ⊂ U. Como P_G (a, b) ∈ B_G y b ∈ P_G (a, b) ⊂ U, resulta que U es una unión de elementos de B_G . Como cada elemento de B_G es abierto en (N, τ_G ), tenemos que B_G es una base del espacio topológico (N, τ_G ). ☑

4. Propiedades del espacio (N, τ_G )

Vamos ahora a mostrar una serie de propiedades del espacio de Golomb (N, τ_G ). Los Teoremas 4.1, 4.2, 4.3, 4.11, 4.28 y 4.29 se mencionaron en la Introducción, y fueron probados por Golomb.

Teorema 4.1. (N, τ_G ) es segundo numerable. Más aún, cada subconjunto abierto y no vacío en (N, τ_G ) es infinito.

Demostración. Por el Teorema 3.2, B_G es una base del espacio topológico (N, τ_G ). Sea A = {(a, b) ∈ N × N:〈a, b〉= 1}. Como N es numerable, N × N también es numerable. Entonces A ⊂ N × N es numerable. Ahora consideremos la función g: A → B_G definida, para (a, b) ∈ A, como g(a, b) = P_G (a, b). Es claro que g es una función sobreyectiva y, como A es numerable, B_G es numerable. Por tanto (N, τ_G ) es segundo numerable.

Sean U un subconjunto abierto y no vacío en (N, τ_G ) y b ∈ U. Como B_G es una base de (N, τ_G ), existe a ∈ N tal que〈a, b〉= 1 y P_G (a, b) ⊂ U. Por la propiedad 1) del Teorema 3.1, P_G (a, b) es infinito. Luego U es infinito. ☑

Teorema 4.2. Para cada p ∈ P, M(p) es cerrado en (N, τG).

Demostración. Como p ∈ P, por el Teorema 2.5,〈p, i〉= 1 para todo i ∈ {1, 2, . . . , p−1}. Por tanto cada conjunto P_G (p, i) es abierto en (N, τ_G ). Además,

La unión ∪ ^p−1 _i=1 P_G (p, i) es un abierto en (N, τ_G ). Entonces N \ M(p) es abierto en (N, τ_G ) y, así, M(p) es cerrado en (N, τ_G ). ☑

Teorema 4.3. El conjunto P es infinito.

Demostración. Por el Teorema de Factorización Única, todo número natural distinto de 1 es múltiplo de algún número primo. Por tanto

Si P es finito, por el Teorema 4.2, ∪ _p∈P M(p) es una unión finita de subconjuntos cerrados en (N, τ_G ). Luego ∪ _p∈P M(p) es cerrado en (N, τ_G ) y, por tanto, N \ {1} es cerrado en (N, τ_G ). Entonces {1} es abierto en (N, τ_G ). Pero esto contradice el hecho de que los subconjuntos abiertos y no vacíos de (N, τ_G ) son infinitos. Por lo tanto, P es infinito. ☑

El siguiente resultado da una condición necesaria y suficiente para que dos elementos de la base B_F se intersequen.

Teorema 4.4. Sean a, c ∈ N y b, d ∈ Z. Entonces P_F (a, b) ∩ P_F (c, d) ≠ ∅ si y sólo si〈a, c〉| (b − d).

Demostración. Supongamos que P_F (a, b)∩P_F (c, d) ≠ ∅. Sean x, y ∈ Z tales que ax+b = cy + d. Luego b − d = cy + a(−x), por lo que b − d es una combinación lineal de a y c. Entonces, por la tercera parte del Teorema 2.3,〈a, c〉| (b − d).

Supongamos ahora que〈a, c〉| (b − d). Entonces existe z ∈ Z tal que b − d = z〈a, c〉. Por la primera parte del Teorema 2.3, existen s, t ∈ Z tales que〈a, c〉= as + ct. Luego b − d = asz + ctz, de donde d + c(tz) = b + a(−sz). Notemos que d + c(tz) ∈ P_F (c, d) y b + a(−sz) ∈ P_F (a, b). Luego P_F (a, b) ∩ P_F (c, d) ≠ ∅. ☑

En la demostración del siguiente resultado utilizamos la Propiedad Arquimediana, la cual dice que si a, b ∈ R y a > 0, entonces existe n ∈ N tal que an > b.

Teorema 4.5. Sean a, b, c, d ∈ N. Entonces P(a, b)∩P(c, d) ≠ ∅ si y sólo si〈a, c〉| (b−d).

Demostración. Supongamos que P(a, b) ∩ P(c, d) ≠ ∅. Sean x, y ∈ N tales que ax + b = cy + d. Luego b − d = cy + a(−x), por lo que b − d es una combinación lineal de a y c. Entonces, por la tercera parte del Teorema 2.3,〈a, c〉| (b − d).

Supongamos ahora que〈a, c〉| (b − d). Entonces existe z ∈ Z tal que b − d = z〈a, c〉. Por la primera parte del Teorema 2.3, existen s, t ∈ Z tales que〈a, c〉= as + ct. Luego b − d = asz + ctz, de donde d + c(tz) = b + a(−sz). Por la Propiedad Arquimediana, existen n ₁, n ₂ ∈ N tales que an ₁ > −tz y cn ₂ > sz. Sea n = máx{n ₁, n ₂}. Entonces an + tz y cn − sz son números naturales. Además

y

Luego, P(c, d) ∩ P(a, b) ≠ ∅. ☑

Corolario 4.6. Sean a, b, c ∈ N. Si〈a, c〉= 1, entonces P(a, b) ∩M(c) ≠ ∅.

Demostración. Como M(c) = P(c, c) y〈a, c〉= 1, tenemos que〈a, c〉| (b − c). Entonces, por el Teorema 4.5, P(a, b) ∩M(c) = P(a, b) ∩ P(c, c) ≠ ∅. ☑

Teorema 4.7. Sean a, b, c, d ∈ N tales que〈a, b〉=〈c, d〉= 1. Entonces P_G (a, b) ∩ P_G (c, d) ≠ ∅ si y sólo si〈a, c〉| (b − d).

Demostración. Supongamos que P_G (a, b) ∩ P_G (c, d) ≠ ∅. Entonces P(a, b) ∩ P(c, d) ≠ ∅ y, por el Teorema 4.5,〈a, c〉| (b − d). Supongamos ahora que〈a, c〉| (b − d). Entonces, por el Teorema 4.5, P(a, b)∩P(c, d) ≠ ∅.Como〈a, b〉=〈c, d〉= 1, tenemos que P(a, b) = P_G (a, b) y P(c, d) = P_G (c, d). Luego P_G (a, b) ∩ P_G (c, d) ≠ ∅. ☑

El Teorema 4.7 aparece en la parte 2. de [¹², Ejemplos 60 y 61, p. 82], y da una condición necesaria y suficiente para que dos elementos de la base B_G se intersequen. Sean a, b, c, d ∈ N tales que〈a, b〉=〈c, d〉= 1. Si〈a, c〉≠ 1 entonces, por el Teorema 4.7,

Teorema 4.8. Sean a, b, c, d, e, f ∈ N. Si〈a, c〉=〈a, e〉=〈c, e〉= 1, entonces P(a, b) ∩ P(c, d) ∩ P(e, f) ≠ ∅.

Demostración. Supongamos que a = 1. Entonces P(a, b) = {b+n: n ∈ N₀} es el conjunto de números naturales mayores o iguales a b. Sean y s, t ∈ Z tales que 1 =〈c, e〉= cs+et. Luego d−f = (cs+et)z = csz+etz, de donde f +e(tz) = d+c(−sz). Por la Propiedad Arquimediana, existen n ₁, n ₂, n ₃ ∈ N tales que cn ₁ > −tz, en ₂ > sz y cn ₃ > −tz+g. Sea n = máx{n ₁, n ₂, n ₃}. Entonces cn ≧ cn ₁ > −tz, por lo que cn+tz ∈ N. También en ≧ en ₂ > sz, de donde en − sz ∈ N. Además cn ≧ cn ₃ > −tz + g, por lo que , luego e(tz + cn) > b − f, de donde f + e(tz + cn) > b. Así, f + e(tz + cn) ∈ P(a, b). Como f + e(tz) + ecn = d + c(−sz) + ecn, tenemos que

y

Luego f + e(tz) + ecn ∈ P(a, b) ∩ P(c, d) ∩ P(e, f), probando así que P(a, b) ∩ P(c, d) ∩ P(e, f) ≠ ∅. Si c = 1 o bien e = 1, procediendo de manera similar se prueba que P(a, b) ∩ P(c, d) ∩ P(e, f) ≠ ∅. Supongamos, por tanto, que a ≧ 2, c ≧ 2 y e ≧ 2. Consideremos el sistema de congruencias lineales

Como〈a, c〉=〈a, e〉=〈c, e〉= 1, por el Teorema Chino del Residuo (Teorema 2.11), existe un único entero k tal que x ≡ k (mód ace). Sean l ₁, l ₂, l ₃, l ₄ ∈ Z tales que x = acel ₁+k, x = al ₂+b, x = cl ₃+d y x = el ₄+f. Luego acel ₁+k = al ₂+b, acel ₁+k = cl ₃+d y acel ₁+k = el ₄+f, de donde k = a(l ₂−cel ₁)+b, k = c(l ₃−ael ₁)+d y k = e(l ₄−acl ₁)+f. Por tanto, k ≡ b (mód a), k ≡ d (mód c) y k ≡ f (mód e).

Por la Propiedad Arquimediana, existen n ₁, n ₂, n ₃ ∈ N tales que cen ₁ > cel ₁−l ₂, aen ₂ > ael ₁ −l ₃ y acn ₃ > acl ₁ −l ₄. Entonces n = máx{n ₁, n ₂, n ₃} es un número natural tal que cen + l ₂ − cel ₁, aen + l ₃ − ael ₁ y acn + l ₄ − acl ₁ son números naturales. Luego

y

Así, k + acen ∈ P(a, b) ∩ P(c, d) ∩ P(e, f), de donde P(a, b) ∩ P(c, d) ∩ P(e, f) ≠ ∅. ☑

Como una aplicación del Teorema 4.5 tenemos el siguiente resultado, el cual aparece en [¹³, Lema 4.1, p. 904].

Teorema 4.9. Sean a, b, c, d ∈ N con b < a. Si P(a, b) ∩ P(c, d) ≠ ∅ y a | c, entonces P(c, d) ⊂ P(a, b).

Demostración. Como P(a, b) ∩ P(c, d) ≠ ∅, por el Teorema 4.5〈a, c〉| (b−d). Sea n ∈ N tal que c = an. Entonces ha, ci = ha, ani = ah1, ni = a. Luego a | (b − d) y, como a > b ≧ 1, tenemos que b ≡ d (mód a). Notemos que a ≧ 2 y c = an implican que c ≧ 2. Sea y ∈ P(c, d). Entonces y ∈ N, c | (y − d) y, como a | c, resulta que a | (y − d). Luego y ≡ d (mód a). Ahora bien, como b ≡ d (mód a) y y ≡ d (mód a), se tiene que y ≡ b (mód a). Luego y ∈ PF (a, b) ∩ N y, por el Teorema 2.8, y ∈ P(a, b). ☑

Como una aplicación del Teorema 4.7, tenemos el siguiente resultado.

Teorema 4.10. Sean a, x, y ∈ N tales que x ≠ y, máx{x, y} < a, 〈a, x〉=〈a, y〉= 1. Entonces P_G (a, x) y P_G (a, y) son abiertos en (N, τ_G ) tales que x ∈ P_G (a, x), y ∈ P_G (a, y) y P_G (a, x) ∩ P_G (a, y) = ∅. Además y ∉ cl_N(P_G (a, x)) .

Demostración. Sean c = máx{x, y} y d = mín{x, y}. Notemos que〈a, a〉= a y que 1 ≦ d < c < a. Como〈a, x〉=〈a, y〉= 1, P_G (a, x) y P_G (a, y) son abiertos en (N, τ_G ) tales que x ∈ P_G (a, x) y y ∈ P_G (a, y). Supongamos que P_G (a, x)∩P_G (a, y) ≠ ∅. Entonces, por el Teorema 4.7, a | (x−y). Esto implica que a | (c−d). Ahora bien, al ser a y c−d enteros positivos, de a | (c − d) se sigue que a ≦ c − d < c. Luego a < c, lo cual contradice la desigualdad c < a. Esto prueba que P_G (a, x)∩P_G (a, y) = ∅ y que y ∉ cl_N(P_G (a, x)) . ☑

El siguiente resultado es consecuencia del Teorema 4.10.

Teorema 4.11. (N, τ_G ) es T ₂.

Demostración. Sean x, y ∈ N con x ≠ y, Como P es infinito, existe p ∈ P tal que máx{x, y} < p. Por el Teorema 2.5,〈p, x〉=〈p, y〉= 1. Luego, por el Teorema 4.10, P_G (p, x) y P_G (p, y) son abiertos en (N, τ_G ) tales que x ∈ P_G (p, x), y ∈ P_G (p, y) y P_G (p, x) ∩ P_G (p, y) = ∅. Por tanto, (N, τ_G ) es T ₂. ☑

Sean a, x ∈ N. En [¹⁵] Szczuka presenta algunos resultados que involucran al conjunto cl_N(P(a, x)) . Por ejemplo, en [¹⁵, Lema 3.3, p. 16] se muestra que si x ₁ ≡ x (mód a), x ₁ ≦ a y〈a, x〉= 1, entonces P_G (a, x ₁) ⊂ cl_N(P_G (a, x)) . En [15, Lema 3.5, p. 16] se prueba que si a y x son impares y〈a, x〉= 1, entonces cl_N(P_G (a, x)) = cl_N(P_G (2a, x)) . En el Teorema 4.10 indicamos condiciones bajo las cuales P_G (a, x) no es denso en (N, τ_G ). Como consecuencia del siguiente resultado, los múltiplos de a se encuentran en cl_N(P_G (a, x)) .

Teorema 4.12. Sean a, x ∈ N tales que〈a, x〉= 1. Entonces, para cada n ∈ N, M(a) ⊂ cl_N(PG(aⁿ, x)) .

Demostración. Sea n ∈ N. Como〈a, x〉= 1, por el Teorema 2.4,〈aⁿ, x〉= 1. Tomemos ab ∈ M(a) y un abierto W en (N, τ_G ) de modo que ab ∈ W. Sea d ∈ N tal que〈d, ab〉= 1 y P_G (d, ab) ⊂ W. Si〈d, aⁿ 〉≠ 1, entonces existe p ∈ P tal que p | d y p | aⁿ . Por el Teorema 2.6, p | a. Entonces p | d y p | ab, de donde〈d, ab〉≠ 1, una contradicción. Luego〈d, aⁿ 〉= 1 y, por consiguiente,〈d, aⁿ 〉| (ab−x). Esto implica, por el Teorema 4.7, que P_G (d, ab) ∩ P_G (aⁿ, x) ≠ ∅. Luego W ∩ P_G (aⁿ, x) ≠ ∅ y, así, ab ∈ cl_N(P_G (aⁿ, x)) . ☑

Corolario 4.13. Para cada d ∈ N, P_G (1, d) es denso en (N, τ_G ).

Demostración. Sean d ∈ N y a = 1. Entonces〈a, d〉= 1, M(a) = N y, por el Teorema 4.12, N = M(a) ⊂ cl_N(P_G (a, d)) , así que P_G (a, d) = P_G (1, d) es denso en (N, τ_G ). ☑

Por el Teorema 4.10 y el Corolario 4.13, entre los miembros BG algunos son densos en (N, τG), y otros no. Es un problema abierto el caracterizar los elementos de BG y los de la forma P(a, b), que son densos en (N, τG).

Teorema 4.14. Si a, b ∈ N, entonces P_F (a, b) ∩ N ⊂ cl_N(P(a, b)) .

Demostración. Notemos que si b ≦ a, entonces por el Teorema 2.8, P_F (a, b) ∩ N = P(a, b) ⊂ cl_N(P(a, b)) . Sea x ∈ P_F (a, b) ∩ N. Entonces existe z ∈ Z tal que x = az + b. Sean U un abierto en (N, τ_G ) y c ∈ N tales que x ∈ U,〈c, x〉= 1 y P_G (c, x) ⊂ U. Como〈c, a〉| a, sucede que〈c, a〉| az. Luego〈c, a〉| (x − b) y, por el Teorema 4.5, P_G (c, x) ∩ P(a, b) = P(c, x) ∩ P(a, b) ≠ ∅. Esto prueba que x ∈ cl_N(P(a, b)) . ☑

Sean a, b ∈ N. Notemos que

En otras palabras, P_F (a, b) ∩ N se consigue uniéndole a P(a, b), aquellos elementos de la progresión aritmética {b − a, b − 2a, b − 3a, . . .} que sean mayores o iguales a uno.

El siguiente resultado aparece en la parte 10. de [¹², Ejemplos 60 y 61, p. 83]. La prueba que presentamos difiere de la dada en [¹²].

Teorema 4.15. Sean c ∈ N y p ∈ P tales que〈p, c〉= 1. Entonces, para cada n ∈ N, cl_N(PG(pⁿ, c)) = M(p) ∪ [P_F (pⁿ, c) ∩ N].

Demostración. Tomemos n ∈ N. Como〈p, c〉= 1, por el Teorema 2.4,〈pⁿ, c〉= 1. Por el Teorema 4.14, P_F (pⁿ, c) ∩ N ⊂ cl_N(P_G (pⁿ, c)) , y por el Teorema 4.12, M(p) ⊂ cl_N(P_G (pⁿ, c)) . Por tanto M(p) ∪ [P_F (pⁿ, c) ∩ N] ⊂ cl_N(P_G (pⁿ, c)) . Para probar la otra contención, sea x ∈ cl_N(P_G (pⁿ, c)) . Entonces x ∈ N y todo abierto básico en (N, τ_G ) que tiene a x, interseca a P_G (pⁿ, c). Luego,

Si p | x, entonces x ∈ M(p). Consideremos, por tanto, que p ∤ x. Sea t = pⁿ . Notemos que〈pⁿ, pⁿ 〉= pⁿ . Supongamos que〈t, x〉=〈pⁿ, x〉≠ 1. Entonces existe q ∈ P tal que q | pⁿ y q | x. Por el Teorema 2.6, q | p. Esto implica que q = p, por lo que p | x, un absurdo. Luego〈t, x〉=〈pⁿ, x〉= 1 y, por (4), P_G (pⁿ, x) ∩ P_G (pⁿ, c) ≠ ∅. Aplicando el Teorema 4.7, deducimos que pn | (x−c), de donde x ∈ P_F (pⁿ, c)∩N. Con esto probamos que cl_N(P_G (pⁿ, c)) ⊂ M(p) ∪ [P_F (pⁿ, c) ∩ N]. ☑

Sean c ∈ N y p ∈ P tales que〈p, c〉= 1. Entonces, para cada n ∈ N tal que c < pⁿ , por los Teoremas 2.8 y 4.15 tenemos que

Sean a, x ∈ N tales que〈a, x〉= 1. Es un problema abierto el describir el conjunto cl_N(P_G (a, x)) . Por el Teorema 4.12, M(a) ∪ P_G (a, x) ⊂ cl_N(P_G (a, x)) . Sin embargo, describir a cl_N(P_G (a, x)) \ (M(a) ∪ P_G (a, x)) parece un problema difícil. Hasta donde se ha investigado, solo se conocen los resultados de Szczuka que hemos mencionado, los Teoremas 4.10, 4.12, 4.15 y el Corolario 4.13.

Teorema 4.16. Para cada d ∈ N, P_G (1, d) es de Brown en (N, τ_G ). En particular, P_G (1, d) es conexo.

Demostración. Sean U y V dos abiertos no vacíos en P_G (1, d). Como P_G (1, d) es abierto en (N, τ_G ), U y V son abiertos en (N, τ_G ). Sean x ∈ U y y ∈ V. Tomemos a, b ∈ N tales que〈a, x〉=〈b, y〉= 1, P_G (a, x) ⊂ U y P_G (b, y) ⊂ V. Si a = 1, entonces P_G (a, x) = {x+n: n ∈ N₀}. Como P_G (b, y) es infinito, existe n ₀ ∈ N₀ tal que y+bn ₀ ≧ x, y entonces

Por tanto, cl _PG (1,d)(U) ∩ cl _PG (1,d)(V ) ≠ ∅. De manera similar, si b = 1 tenemos que cl _PG (1,d)(U)∩clP_G (1,d)(V ) ≠ ∅. Ahora supongamos que a ≧ 2 y b ≧ 2. Por el Teorema 4.12, M(a) ⊂ cl_N(P_G (a, x)) y M(b) ⊂ cl_N(P_G (b, y)) . En particular, abd ∈ cl_N(P_G (a, x)) ∩ cl_N(P_G (b, y)) . Como a ≧ 2 y b ≧ 2, tenemos que d < abd, así que abd ∈ P_G (1, d). Luego

Por tanto, cl _PG (1,d)(U) ∩ cl _PG (1,d)(V ) ≠ ∅ y, así, P_G (1, d) es de Brown en (N, τ_G ). Como los espacios de Brown son conexos, P_G (1, d) es conexo. ☑

A continuación presentamos una prueba explícita de lo que M. Brown afirmó en el resumen de la plática que impartió en abril de 1953, y que comentamos en la Introducción.

Teorema 4.17. (N, τ_G ) es de Brown. En particular, (N, τ_G ) es conexo y no es T _2½.

Demostración. Como P_G (1, 1) = N, el resultado se sigue del Teorema 4.16 y del hecho de que los espacios de Brown son conexos y no T _2½. ☑

Sería interesante caracterizar los subconjuntos de (N, τ_G ) que son de Brown. En particular, caracterizar los conjuntos de la forma P_G (a, b) y/o P(a, b) que son de Brown en (N, τ_G ). Como vimos en el Teorema 4.16, hay elementos de B_G que son de Brown. En el Teorema 4.18 mostramos que también hay elementos de B_G que no son de Brown.

Hemos demostrado que la conexidad del espacio (N, τ_G ) es consecuencia del hecho de que es de Brown. Existen otras propiedades que implican la conexidad. Por ejemplo, un espacio topológico X es hiperconexo si todo subconjunto abierto y no vacío de X, es denso en X. Decimos que X es ultraconexo si para cada x, y ∈ X con x ≠ y, se cumple que cl _X ({x}) ∩ cl _X ({y}) ≠ ∅. Si X es hiperconexo, entonces X no contiene dos subconjuntos abiertos, ajenos y no vacíos. Por otro lado, si X es ultraconexo, entonces X no es T ₁ y, en consecuencia, tampoco T ₂. Por lo tanto, todo espacio hiperconexo o ultraconexo es conexo pero no T ₂. No es complicado ver que todo espacio hiperconexo o ultraconexo es de Brown. El recíproco de esta afirmación no es cierto, pues como hemos visto, (N, τ_G ) es de Brown y T ₂, por lo que dicho espacio no es hiperconexo ni ultraconexo.

Por [⁴, Teoremas 3.1.9 y 3.3.1], los espacios compactos y T ₂, así como los espacios localmente compactos y T ₂, son T ₄ y por tanto T _2½. Entonces (N, τ_G ) no es compacto ni localmente compacto. Estas observaciones también fueron hechas por Golomb en [⁷, Teorema 5] y [⁸, Teorema 5], aunque con demostraciones distintas a las que hemos presentado. Sería interesante determinar si (N, τ_G ) posee alguna propiedad de compacidad.

El siguiente resultado muestra que una buena cantidad de elementos de la forma P_G (p, c), donde p ∈ P, no son conexos en (N, τ_G ). Hasta donde hemos investigado, el siguiente resultado aparece en la literatura por primera vez.

Teorema 4.18. Sean c ∈ N y p ∈ P con〈p, c〉= 1. Tomemos a, b ∈ P_G (p, c) tales que a < b y n,m ∈ N₀, de modo que a = pm+ c, b = pn + c y 0 ≦ m < n. Entonces

son abiertos en (N, τ_G ) y tales que a ∈ U, b ∈ V, U ∩ V = ∅ y P_G (p, c) = U ∪ V. En particular, P_G (p, c) no es conexo ni de Brown.

Demostración. Tomemos c, p, a, b, n y m como se indica en el teorema. Como p ∈ P y〈p, c〉= 1, el Teorema 2.7 garantiza que〈p^{n +1}, pi + c〉= 1, para cada i ∈ N₀. Entonces podemos considerar los conjuntos U y V que se indican en (5), y estos son abiertos en (N, τ_G ). La propiedad 1) del Teorema 3.1 asegura que U y V son conjuntos infinitos. Como 0 ≦ m < n < 2 ⁿ ≦ pⁿ , tenemos que m+ 1 ≦ n ≦ pⁿ − 1. Por tanto,

y

Es decir, a ∈ U y b ∈ V. Para verificar que U y V son ajenos, supongamos, por el contrario, que existe z ∈ U ∩ V. Sean i ∈ {0, 1, . . . ,m} y j ∈ {m+ 1,m+ 2, . . . , pⁿ − 1} tales que z ∈ PG(p^{n +1}, pi + c) y z ∈ PG(p^{n +1}, pj + c). Como p^{n +1} > 1, pues p es un número primo, tenemos que

La transitividad de la congruencia y los incisos 1) y 3) del Teorema 2.10 implican que pi + c ≡ pj + c (mód p^{n +1}), de donde pi ≡ pj (mód p^{n +1}). Luego i ≡ j (mód pn). Sin embargo, como el conjunto A = {0, 1, . . . ,m,m+1, . . . , pⁿ −1} es un sistema completo de residuos módulo pⁿ , ningún par de elementos distintos de A son congruentes módulo pⁿ . En particular, como i ≦ m < m+1 ≦ j, resulta que i ≢ j (mód pⁿ ). De esta contradicción se infiere que U ∩ V = ∅.

Vamos a probar ahora que U ∪ V = P_G (p, c). Si z ∈ U, entonces existe i ∈ {0, 1, . . . ,m} tal que z ∈ P_G (p^{n +1}, pi + c). Tomemos z ₀ ∈ N₀ de modo que z = p^{n +1} z ₀ + pi + c. Entonces z = p(pⁿz ₀ + i) + c ∈ P_G (p, c). De manera similar, si z ∈ V, existe j ∈ {m+ 1,m+ 2, . . . , pn − 1} tal que z ∈ P_G (p^{n +1}, pj + c). Al tomar z ₁ ∈ N₀ de modo que z = p^{n +1} z ₁ + pj + c, deducimos que z = p(pⁿz ₁ + j) + c ∈ P_G (p, c). Esto prueba que U ∪ V ⊂ P_G (p, c).

Para probar la otra contención, sea z ∈ P_G (p, c). Entonces existe k ∈ N₀ para el cual z = pk + c. Por el Algoritmo de la División (Teorema 2.1) aplicado a k y pⁿ , existen s, t ∈ N₀ de manera que k = pⁿs + t y 0 ≦ t < pⁿ . Así obtenemos

Como 0 ≦ t < pⁿ y 0 ≦ m < pⁿ , se sigue que

Luego, de (6),

Esto prueba que P_G (p, c) ⊂ U ∪V y, como la otra contención también es cierta, U ∪V = P_G (p, c). Así probamos la primera parte del teorema. Ahora bien, como el conjunto P_G (p, c) ha sido escrito como la unión de dos conjuntos abiertos en (N, τ_G ), que además son ajenos y no vacíos, P_G (p, c) no es conexo. Como los espacios de Brown son conexos, P_G (p, c) no es de Brown. ☑

Sean c ∈ N y p ∈ P tales que〈p, c〉= 1. Tomemos a, b ∈ P_G (p, c) de modo que b < a. Usando las mismas ideas que mostramos en la prueba del Teorema 4.18, se sigue que existen abiertos U y V en (N, τ_G ) tales que a ∈ U, b ∈ V, U ∩ V = ∅ y P_G (p, c) = U ∪ V. Tenemos, por tanto, el siguiente resultado.

Teorema 4.19. Sean c ∈ N y p ∈ P tales que〈p, c〉= 1. Tomemos a, b ∈ P_G (p, c) de modo que a ≠ b. Entonces existen abiertos U y V en (N, τ_G ) tales que a ∈ U, b ∈ V, U ∩ V = ∅ y P_G (p, c) = U ∪ V. En otras palabras, P_G (p, c) está totalmente separado.

Como los espacios totalmente separados son hereditariamente disconexos, para cada c ∈ N y p ∈ P con〈p, c〉= 1 el conjunto PG(p, c) es hereditariamente disconexo. Utilizando esto, presentamos algunas consecuencias del Teorema 4.19. Como mencionamos en la Introducción, en 1969 Kirch probó que (N, τG) no es localmente conexo en 1. En el siguiente teorema generalizamos este resultado.

Teorema 4.20. Para ningún d ∈ N, P_G (1, d) es conexo en pequeño, o bien casi conexo en pequeño en todos sus puntos.

Demostración. Sea d ∈ N y supongamos, por el contrario, que P_G (1, d) es conexo en pequeño, o bien casi conexo en pequeño en algún punto c ∈ P_G (1, d). Definimos un conjunto P_G (p, c) como sigue: si c es impar, sea p = 2. Si c es par, tomamos p ∈ P tal que c < p. En cualquier caso, p ∈ P,〈p, c〉= 1 y P_G (p, c) es un subconjunto abierto de P_G (1, d) tal que c ∈ P_G (p, c). Como P_G (1, d) es conexo en pequeño o bien casi conexo en pequeño en c, existe un subconjunto conexo C de P_G (1, d) tal que int _PG(1,d)(C) ≠ ∅ y C ⊂ P_G (p, c). Al ser P_G (1, d) abierto en (N, τ_G ), tenemos que int_N(C) ≠ ∅. Como los subconjuntos abiertos y no vacíos de (N, τ_G ) son infinitos, el conjunto C es infinito. Esto contradice el hecho de que P_G (p, c) es hereditariamente disconexo. Por tanto, P_G (1, d) no es conexo en pequeño ni casi conexo en pequeño en c. ☑

Corolario 4.21. (N, τ_G ) no es conexo en pequeño ni casi conexo en pequeño en ninguno de sus puntos. En particular (N, τ_G ) no es localmente conexo.

Demostración. Como P_G (1, 1) = N, la primera parte se sigue del Teorema 4.20. Si (N, τ_G ) es localmente conexo, entonces (N, τ_G ) es conexo en pequeño en cada uno de sus puntos, lo cual contradice el Teorema 4.20. ☑

Hemos visto que la base B_G posee elementos que son conexos, y también elementos que son hereditariamente disconexos. Sería interesante poder encontrar condiciones necesarias y suficientes bajo las cuales dos elementos de B_G son homeomorfos. Incluso encontrar condiciones bajo las cuales un elemento de B_G sea una imagen continua de otro elemento de B_G .

Para a ∈ N, definimos Θ(a) = {p ∈ P: p | a}. Observemos que Θ(1) = ∅. El siguiente resultado aparece en [¹³, Teorema 3.3]. La prueba que presentamos es diferente, e incluso más corta, a la dada en el artículo [¹³], pues utilizamos el Teorema 4.19.

Teorema 4.22. Sean a, b ∈ N. Entonces P(a, b) es conexo en (N, τ_G ) si y sólo si Θ(a) ⊂ Θ(b). En particular,

Demostración. Supongamos que P(a, b) es conexo. Si Θ(a) no es un subconjunto de Θ(b), entonces a > 1 y existe p ∈ Θ(a) tal que p ∉ Θ(b). Luego p es un número primo que divide a a pero no a b. Por tanto,〈p, b〉= 1. Como p | a, tenemos que P(a, b) ⊂ PG(p, b). Del Teorema 4.19 se sigue que PG(p, b) es hereditariamente disconexo, así que P(a, b) posee solo un elemento, lo cual es una contradicción. Esto prueba que Θ(a) ⊂ Θ(b).

Ahora supongamos que Θ(a) ⊂ Θ(b). Si P(a, b) no es conexo, entonces existen dos subconjuntos no vacíos O ₁ y O ₂ de P(a, b), abiertos en el subespacio P(a, b) de (N, τ_G ) y tales que P(a, b) = O ₁ ∪ O ₂ y O ₁ ∩ O ₂ = ∅. Sean U ₁ y U ₂ abiertos en (N, τ_G ) tales que O ₁ = U ₁ ∩ P(a, b) y O ₂ = U ₂ ∩ P(a, b). Consideremos b ₁ ∈ O ₁ y b ₂ ∈ O ₂. Como b ₁ ∈ U ₁, b ₂ ∈ U ₂ y tanto U ₁ como U ₂ son abiertos en (N, τ_G ), existen a ₁, a ₂ ∈ N tales que〈a ₁, b ₁〉=〈a ₂, b ₂〉= 1, PG(a ₁, b ₁) ⊂ U ₁ y PG(a ₂, b ₂) ⊂ U ₂.

Vamos a probar que〈a, a ₁〉= 1. Para esto, supongamos que〈a, a ₁〉≠ 1. Entonces existe p ∈ P tal que p | a y p | a ₁. Luego p ∈ Θ(a) y, como Θ(a) ⊂ Θ(b), tenemos que p ∈ Θ(b). Luego p | b y p | a ₁. Ahora bien, como b ₁ ∈ O ₁ ⊂ P(a, b), existe n ₁ ∈ N tal que b ₁ = an ₁ + b. En vista de que a y b son múltiplos de p, de la igualdad b ₁ = an ₁ + b, se sigue que p | b ₁. Luego p | a ₁ y p | b ₁, de donde p |〈a ₁, b ₁〉, es decir p | 1. Esto es un absurdo, luego〈a, a ₁〉= 1. De manera similar, se prueba que〈a, a ₂〉= 1. Luego, por el Corolario 4.6,

Ahora vamos a probar que P(a, b) ∩ M(a ₁) ⊂ O ₁. Tomemos un elemento d ∈ P(a, b) ∩ M(a ₁). Como P(a, b) = O ₁ ∪ O ₂, tenemos que d ∈ O ₁ o bien d ∈ O ₂. Supongamos que d ∈ O ₂. Entonces d ∈ U ₂ y, como U ₂ es abierto en (N, τ_G ), existe c ∈ N tal que〈c, d〉= 1 y P_G (c, d) ⊂ U ₂. Si existe p ∈ P tal que p | c y p | a ₁, entonces, como d es un múltiplo de a ₁ y p | a ₁, tenemos que p | d. Luego p | c y p | d, de donde p |〈c, d〉, es decir p | 1. Esto es absurdo, así que〈c, a ₁〉= 1. Ahora supongamos que existe p ∈ P tal que p | a y p | c. Como Θ(a) ⊂ Θ(b) y p ∈ Θ(a), tenemos que p ∈ Θ(b). Luego p | b y, en vista de que d ∈ P(a, b) y tanto a como b son múltiplos de p, tenemos que p | d. Entonces p | c y p | d, de donde p |〈c, d〉. Así p | 1, lo cual es absurdo. Esto prueba que〈a, c〉= 1.

Notemos que a, c, y a ₁ son números naturales tales que〈a ₁, c〉=〈a ₁, a〉=〈c, a〉= 1. Entonces, por el Teorema 4.8, PG(a ₁, b ₁) ∩ PG(c, d) ∩ P(a, b) ≠ ∅. Esto implica que

Luego O ₁ ∩ O ₂ ≠ ∅, lo cual es una contradicción. Entonces d ∈ O ₁, probando con esto que P(a, b)∩M(a ₁) ⊂ O ₁. De manera similar se prueba que P(a, b)∩M(a ₂) ⊂ O ₂. Como〈a, a ₁〉=〈a, a ₂〉= 1, por el Teorema 2.4, ha, a ₁ a ₂ i = 1. Luego, por el Corolario 4.6, P(a, b) ∩M(a ₁ a ₂) ≠ ∅. Ahora bien, notemos que

Esto contradice el hecho de que O ₁ ∩ O ₂ = ∅. Dicha contradicción proviene de suponer que P(a, b) no es conexo. Por tanto, P(a, b) es conexo.

Para probar 1), notemos que M(a) = P(a, a) y, como Θ(a) ⊂ Θ(a), por la primera parte del teorema M(a) es conexo en (N, τ_G ).

Para probar 2) supongamos primero que〈a, b〉= 1 y que PG(a, b) es conexo. Entonces, por la primera parte del teorema, Θ(a) ⊂ Θ(b). Si a ≧ 2, entonces existe p ∈ P tal que p | a, por lo que también p | b, contradiciendo que〈a, b〉= 1. Luego a = 1. El recíproco se sigue del Teorema 4.16. ☑

A continuación presentamos un resultado que pertenece a la Teoría Analítica de Números, y es llamado el Teorema de Dirichlet.

Teorema 4.23. Sean a, b ∈ N con a > 1 y〈a, b〉= 1. Entonces existe una cantidad infinita de números primos p, para los cuales p ≡ b (mód a).

La prueba del Teorema de Dirichlet utiliza propiedades de ciertas funciones multiplicativas, y varios resultados sobre aritmética de números complejos. En vista de que es bastante dispendiosa, no suele incluirse en textos clásicos de Teoría de Números. Una prueba detallada se puede consultar en [¹, Sección 7.3, p. 148].

Sean a, b ∈ N con a > 1 y〈a, b〉= 1. Tomemos p ∈ P. Notemos que p ≡ b (mód a) si y sólo si p ∈ P_F (a, b) ∩ P. Por tanto, en términos de los elementos de la base B_F de τ_F el Teorema de Dirichlet dice que si a, b ∈ N son tales que a > 1 y〈a, b〉= 1, entonces el conjunto P_F (a, b) ∩ P es infinito. Si a = 1, entonces P_F (a, b) ∩ P es infinito, pues P_F (a, b) = P_F (1, b) = Z y, por tanto, P_F (a, b)∩P = P es infinito (Teorema 4.3). Tenemos entonces que

Utilizaremos (⋆) para probar que, en el espacio (Z, τ_F ), la cerradura del conjunto P₀ = {±p: p ∈ P} es P₀ ∪ {−1, 1}. Los elementos de P₀ se llaman enteros primos.

Teorema 4.24. cl_{(Z, τF )}(P₀) = P₀ ∪ {−1, 1}.

Demostración. Sea b ∈ Z \ {−1, 0, 1}. Hagamos a = 2|b|, donde |b| es el valor absoluto de b. Entonces |b| = b si b ≧ 0, mientras que |b| = −b si b < 0. Por esta razón, podemos decir que |b| = ±b. Ahora bien, x ∈ P_F (a, b) si y sólo si existe n ∈ Z tal que

Como b ∈ Z \ {−1, 0, 1}, el producto b(1±2n) es un entero primo si y sólo si n = 0, caso en el cual dicho número coincide con b. Por tanto,

Esto muestra que si b ∈ Z \ {−1, 0, 1} y, además, b ∉ P₀, entonces P_F (2|b|, b) es un abierto en (Z, τ_F ) que tiene a b y no interseca a P₀. Luego, b ∉ cl_{(Z, τF )}(P₀). Naturalmente P₀ ⊂ cl_{(Z, τF )}(P₀), por lo que, para determinar cl(Z,τ_F )(P₀), solo debemos verificar si contiene los enteros −1, 0 y 1. Notemos que P_F (4, 0) es un abierto en (Z, τ_F ) que tiene a 0. Como P_F (4, 0) = {4z: z ∈ Z} es el conjunto de los enteros que son múltiplos de 4, resulta que P_F (4, 0)∩P₀ = ∅. Luego 0 ∉ cl_{(Z,τF )}(P₀). Consideremos ahora un abierto U en (Z, τ_F ) tal que 1 ∈ U. Entonces existe c ∈ N tal que P_F (c, 1) ⊂ U. Como〈c, 1〉= 1, por (⋆) P_F (c, 1) ∩ P ≠ ∅. En particular U ∩ P₀ ≠ ∅. Esto prueba que 1 ∈ cl_{(Z,τF )}(P0). De manera similar se prueba que −1 ∈ cl_{(Z,τF )}(P0). Por consiguiente, cl_{(Z,τF )}(P₀) = P₀∪{−1, 1}. ☑

Corolario 4.25. cl_{(Z,τF )}(P) = P ∪ {−1, 1} y cl_{(N,(τF )N)}(P) = P ∪ {1}, donde (τ_F )_N es la topología relativa de (Z, τ_F ) a N.

Demostración. Como P ⊂ P₀, por el Teorema 4.24,

Por tanto, para determinar cl_{(Z,τF )}(P), debemos verificar si contiene los enteros −1, 1 y los de la forma −p, donde p ∈ P. Sea U un abierto en (Z, τ_F ) tal que 1 ∈ U. Entonces existe c ∈ N tal que P_F (c, 1) ⊂ U. Como〈c, 1〉= 1, por (⋆) P_F (c, 1) ∩ P ≠ ∅. En particular, U ∩ P ≠ ∅. Esto prueba que 1 ∈ cl_{(Z,τF )}(P). De manera similar se prueba que −1 ∈ cl_{(Z,τF )}(P). Supongamos ahora que p ∈ P. Notemos que x ∈ P_F (3p,−p) si y sólo si existe n ∈ Z tal que x = 3pn − p = p(3n − 1). Como p ∈ P para ningún n ∈ Z, el producto p(3n − 1) es un número primo. Por tanto, P_F (3p,−p) es un abierto en (Z, τ_F ) tal que −p ∈ P_F (3p,−p) y P_F (3p,−p)∩P = ∅. Luego, −p ∉ cl_{(Z,τF )}(P). Esto prueba que cl_{(Z,τF )}(P) = P ∪ {−1, 1}. Para probar la segunda parte, notemos que

En el Corolario 4.25 indicamos que la cerradura de P en el espacio (N, (τ_F )N) es P ∪ {1}, por lo que P no es denso en (N, (τ_F )N). Como mostramos en el Teorema 4.28, P es denso en (N, τ_G ). Para probar esto necesitamos unos resultados previos.

Teorema 4.26. Las siguientes afirmaciones son equivalentes:

Demostración. Es claro que 1) implica 2). Supongamos ahora que 2) se cumple. Sea P_G (a, b) ∈ B_G . Por 2), existe n ₁ ∈ N tal que an ₁+b ∈ P. Como a < an ₁+b y an ₁+b ∈ P, por el Teorema 2.5〈a, an ₁+b〉= 1. Entonces P_G (a, an ₁+b) ∈ B_G y, por 2), existe n ₂ ∈ N tal que an ₂+(an ₁+b) = a(n ₂+n ₁)+b ∈ P. Entonces P_G (a, b) contiene por lo menos dos números primos, a saber an ₁+b y a(n ₂+n ₁)+b. Como a < a(n ₂+n ₁)+b y a(n ₂+n ₁)+b ∈ P, por el Teorema 2.5〈a, a(n ₂ + n ₁) + b〉= 1. Por tanto, P_G (a, a(n ₂ + n ₁) + b) ∈ B_G y, por 2), existe n ₃ ∈ N tal que an ₃ + a(n ₂ + n ₁) + b = a(n ₃ + n ₂ + n ₁) + b ∈ P. Entonces P_G (a, b) contiene por lo menos tres números primos, a saber an ₁, a(n ₂+n ₁)+b y a(n ₃ + n ₂ + n ₁) + b. Continuando de esta manera, resulta que el conjunto P_G (a, b) contiene una cantidad infinita de números primos. Esto muestra que 2) implica 1). ☑

El Teorema de Dirichlet (Teorema 4.23) se puede enunciar en términos de elementos de la base B_G . Dado P_G (a, b) ∈ B_G , con a > 1, el Teorema de Dirichlet asegura que PG(a, b) contiene una cantidad infinita de números primos. Si a = 1 y b ∈ N, entonces〈a, b〉= 1 y P_G (a, b) = {b, b + 1, b + 2, . . .} contiene una cantidad infinita de números primos. Por tanto, para cada P_G (a, b) ∈ B_G se tiene que P_G (a, b) contiene una cantidad infinita de números primos. Con esta observación será más práctico probar la siguiente equivalencia.

Teorema 4.27. El Teorema de Dirichlet es equivalente a afirmar que P es denso en (N, τ_G ).

Demostración. Supongamos que el Teorema de Dirichlet es cierto. Para ver que P es denso en (N, τ_G ), sea U un abierto no vacío en (N, τ_G ). Tomemos b ∈ U y a ∈ N de modo que〈a, b〉= 1 y P_G (a, b) ⊂ U. Como el Teorema de Dirichlet es válido, P_G (a, b) contiene una cantidad infinita de números primos. En particular P_G (a, b) ∩ P ≠ ∅. Luego U ∩ P ≠ ∅. Esto prueba que P es denso en (N, τ_G ).

Ahora supongamos que P es denso en (N, τ_G ). Sean P_G (a, b) ∈ B_G y c ∈ P_G (a, b) tales que c ≠ b. Por la parte 2) del Teorema 3.1,〈a, c〉= 1 y P_G (a, c) ⊂ P_G (a, b). Como P_G (a, c) es un abierto no vacío en (N, τ_G ) y P es denso en (N, τ_G ), sucede que P_G (a, c) ∩ P ≠ ∅. Esto implica que existe n ∈ N tal que an+b ∈ P y, por el Teorema 4.26, P_G (a, b) contiene una cantidad infinita de números primos. Por tanto, el Teorema de Dirichlet se cumple. ☑

El Teorema 4.27 indica que una afirmación aritmética (el Teorema de Dirichlet, en este caso) es equivalente a una afirmación topológica (que P es denso en (N, τ_G )). Como el Teorema de Dirichlet es cierto, por el Teorema 4.27, tenemos el siguiente resultado.

Teorema 4.28. P es denso en (N, τ_G ).

Si podemos probar el Teorema 4.28, sin utilizar el Teorema de Dirichlet, posiblemente usando solamente argumentos topológicos, entonces por el Teorema 4.27 tendremos una demostración, en este caso topológica, del Teorema de Dirichlet. Como ya indicamos, la prueba que se conoce del Teorema de Dirichlet es compleja, por lo que resulta interesante saber si se pueden dar demostraciones alternativas y menos complicadas. Tanto en [⁷] como en [⁸], Golomb pregunta si es posible probar el Teorema 4.28, sin utilizar el Teorema de Dirichlet. Hasta donde sabemos, el problema permanece abierto.

El siguiente resultado asegura que P tiene interior vacío. En particular, P no es abierto en (N, τ_G ).

Teorema 4.29. No existe un abierto no vacío U en (N, τ_G ) tal que U ⊂ P.

Demostración. Supongamos que existe un abierto no vacío U en (N, τ_G ) tal que U ⊂ P. Tomemos b ∈ U y a ∈ N de manera que〈a, b〉= 1 y P_G (a, b) ⊂ U. Entonces cada miembro de P_G (a, b) es un número primo. En particular, b ≧ 2 y el elemento a(a + b + 1) + b, de P_G (a, b), es primo. Sin embargo, como a + 1 ≧ 2, a + b ≧ 3 y

así, el número a(a + b + 1) + b es compuesto. De esta contradicción deducimos que no existe un abierto no vacío U en (N, τ_G ) tal que U ⊂ P. ☑

Un espacio topológico X es homogéneo si para cada x, y ∈ X existe un homeomorfismo f: X → X tal que f(x) = y. Es un problema abierto el determinar si (N, τ_G ) es homogéneo.