Introduction
The ASTM D6236-11 (ASTM International, 2011) guide states that control of the final resistance of Soil Cement (SC) must be carried out by extracting nuclei in the field after its maturation stage, and that its results must be compared with a mixture design validated in a laboratory (Emmert et al. 2017). However, the resistance of Soil Cement (SC) is influenced by multiple factors, such as the type of cement and its quantity in the mix, the water content, the degree of compaction, the uniformity of the compacted layer, the curing conditions, and the age of maturity (Ghanizadeh, Rahrovan, and Bafghi, 2018; Linares-Unamunzaga, Pérez-Acebo, Rojo, and Gonzalo-Orden, 2019; Estarbragh and Ranjbari, 2017). That is why waiting for the mixture to reach 28 days of age is a method that delays the construction process of any infrastructure project.
In order to speed up the construction procedure, the ACI 230 Committee (2009), recommends carrying out a density control on site as soon as the compaction process is completed, either by the ASTM D2922 nuclear method (ASTM International, 2005), the ASTM D1556 sand cone method (ASTM International, 2015a) or the ASTM D2167 rubber ball method (ASTM International, 2015b). However, for any of the above, the test requires fracturing of the compacted layer to open a hole in the surface, causing the bonds that form between the cement and the ground to break during the first adjustment. This results in early microcracking.
This pathology is accompanied by the plastic behavior of the soil type, since it causes contraction and subsequent cracking during the drying process, thus increasing the surface roughness. To prolong the life cycle, it is necessary to maintain a relationship between the smoothness of the pavement and its resistance. As a road gets rougher there is a greater resistance to rolling between the pavement and the vehicle, thus affecting its durability (Akbarian et al., 2019). A bituminous layer is applied to reduce friction, but the cracks leave a scar on the surface, which reduces its useful life.
In order to avoid the extraction of nuclei and the fracturing of the layer during the control of field densities, an analysis of the SC layer as a material whose resistance is acquired through an exothermic reaction is proposed. Although hydraulic cement is known to be composed of calcium silicate phases, Alita and Belita, the former reacts relatively quickly with water and is responsible for the first resistances after a process of heat release due to multiple simultaneous chemical reactions. The second is less reactive at early ages but contributes to strength later on. In order to meet the requirements of current infrastructure works, industrialized cements have an increasingly high content of Alita, and the temperature of the mixture is increased during the adjustment process to achieve high early resistances. (Concrete Sustainability Hub, 2014; Teixeira, Santilli, and Puente, 2016).
On the other hand, it is known that, in addition to the evolution of heat due to the exothermic reaction of cement, ambient temperature has a direct impact on the evolution of mechanical resistance. Experimental tests have revealed that concrete achieves a higher resistance when exposed to high temperatures (40 °C), whereas the opposite occurs when it cures at low temperatures (5 °C). This is how Yikici and Chen (2015) recorded controlled temperature monitoring in massive concrete, where they identified that, in the places near the surface, the temperature of the mix was closer to the ambient temperature, and therefore the resistance of the nuclei extracted from the center registered higher resistances than those taken near the surface (Boubekeur, Ezziane, and Kadri, 2014).
Furthermore, the production of hydraulic cement appropriates the development of additions, also known as Supplemental Cementitious Materials (SCM), such as Nanosilica (NS), fly ash, silica fumes, among others, to improve efficiency and reduce Clinker consumption. Furthermore, since the content of nanoparticles in hydraulic cement improves the development of compression strengths, this reduces the number, degree of crystallinity, and size of portlandite crystals, causing a high pozzolane activity that accelerates the formation of Tobermorite (CHS) and the process of hydration, which results in a reduction of the heat of hydration in the mixture (Juenger et al., 2012; Sánchez Cotte, Torres Chueco, and Esquivel Ramírez, 2019; Abdolhosseini Qomi, Bauchy, and Pellenq, 2018).
Consequently, in order to guarantee environmental sustainability as a goal for 2030, hydraulic cement producers are studying the incorporation of pozzollanic materials from industrial waste to reduce emissions of CO2 (United Nations, 2015). These include masonry waste and other ceramics, since they indicated a clear variation in the thermal properties of the mixture, improving its resistance and increasing the density of the final product. (Pérez Carrión, Baeza Brotons, Garcés Terradillos, Galao Malo, and Payá Bernabeu, 2013). All this in order to promote the recycling of materials during the construction and rehabilitation of pavements. (Zhang, Han, Yu, and Wei, 2018; Silva, Izquierdo, and Delvasto, 2019; Pérez Carrión et al., 2013; Jones, Louw, and Wu, 2015; Tobón, Restrepo Baena, and Payá Bernabeu, 2007).
To summarize, a wide variety of added cements are available which, depending on their mechanical performance, register a greater or lesser release of heat during their adjustment, tracing a different temperature curve. But, while it is true that the resistant capacity of the Soil Cement layer should be measured as the amount of deformation that is recoverable or resistant to a dynamic cyclic load of vehicular traffic, and not as a point compression load, it is proposed that its resistance is correlated with a resilient module (Mr), since it is an important factor when designing thicknesses according to the empirical-mechanical pavement design guide. This becomes a measure of how the proposed pavement should react and of the tracing underlying rapidly applied loads, such as the ones related to traffic. (AASHTO, 2020) and (Reeder, Harrington, Ayers, and Adaska, 2019).
That is why it is estimated that the resilience of a SC mix is determined by the cement content and the density after compaction measured with field tests, where a low density implies a lower Mr. Therefore, the resistance modulus is a function of the development of strengths after an exothermic reaction, which is related to the Alite content, the content and type of the supplemental cement material or addition, and the ambient temperature where the layer was installed.
To evaluate this hypothesis, three commercially available hydraulic cements were chosen: general-purpose cement (UG), high early resistances (ART) and moderate heat of hydration (MCH). These are standardized by NTC 121 (Icontec International, 2014), as a modified adoption of ASTM C1157 (ASTM International, 2020). Each one presents a different development of maturity, resistance and heat of hydration, since they are materials valued for their mechanical performance and not for their chemical product.
Experimental Program
Mixture proportioning
The procedure began with the design of the mixture with each type of cement whose compressive strength is adjusted to 4,5 MPa at 7 days of age. The employed soil was a selected material (A-25), classified as coarse sand with low compressibility clay, which, for this work, constituted a constant in the investigation and abode by the ACI 230 procedure. The following dose was established for each of type of cement:
Soil Cement maturity
The term 'maturity' is understood as the relationship between the evolution of concrete strength as a function of age with the development of temperature (Sota, Avid, Moreira, and Chury, 2016). The method for defining concrete maturity is standardized by ASTM C1074-19 (ASTM International, 2019), and it is used to project and estimate hydraulic concrete strengths by recording the history of temperatures taken on site from the time the mixture is prepared to its final ripening (Lee and Hover, 2016).
In total, 54 cylinders were made for each mix design. 18 were cured in a humid room with a controlled temperature of 11 °C, 18 in a humid room at 30 °C, and the remaining 18 at 40 °C. These samples failed single compression at 1, 3, 4, 8, 16 and 32 days of age, in a series of three cylinders for each age, as described in procedure ASTM C1074-19. According to current test standards, there are two ways of determining the maturity of concrete strength, which measure how temperature affects the hydration rate. The first one assumes that the rate of hydration is a linear function of temperature, while the second, that it obeys the Arrhenius exponential equation (Icontec International, 2002).
The resistance prediction model, which assumes a linear function, is based on the temperature factor and applies the maturity index equation (Equation 1):
where M is the maturity index that can be measured in days or hours; T α is the average of the monitored temperature of the concrete in a time interval Δt; T 0, the calculated reference temperature; and Δ t is the time interval in which the temperature recording was performed.
The Arrhenius exponential equation, in turn, determines the equivalent age with the following Equation 2:
where t e is the age equivalent to the specified temperature T s in hours, Q is the activation energy divided by the gas constant in degrees Kelvin, and T α is the average temperature of the concrete in degrees Kelvin over a time interval Δ t of one hour, T s is the temperature specified in the prediction in degrees Kelvin, and Δ t is the time interval in hours.
With the results obtained from the compression test of cubes, after making the graphs of the inverse of the resistance as a function of the inverse of the temperature and the calculation of the Limit Resistance (Su) and the constant K, we proceeded to estimate the value of the constant Q from the linear curve of the logarithm of K as a function of the inverse of the temperature in degrees Kelvin.
The slope of each of the lines in Figure 1 corresponds to the activation energy value divided by the gas constant Q, so that, for the SC made with ART cement, it amounted to 3 056,2 K, 2 227 K for the SC with UG cement, and 1 711,6 K for the SC with MCH cement. These values were multiplied by the constant of Arrhenius ideal gases (8,31J/(K.mol)). The obtained activation energy of the SC-ART was 25 397; for the SC-UG, 18 511; and for the SC- MCH, 14 223 (Hernandez and Lizarazo Salamanca, 2019). For a Portland cement, this value is usually between 40 000 and 45 000 J/mol (ASTM International, 2019). Therefore, the activation energy of the samples was significantly reduced due to the influence of the soil and the low water content in the reaction.
Temperature monitoring
Temperature monitoring was carried out during the first 30 hours of mixing. The samples, compacted in paper containers, were measured so that the external temperature was transferred to their interior. The container was 10 cm in diameter and 5 cm in height, and the material was compacted into three layers, each 2 cm tall, using a metal rammer with a mass of 340 g with a flat circular surface and a 25 mm diameter (Hernández and Lizarazo Salamanca, 2019). Then, the samples were placed in three humid rooms: the first, at a temperature of 40 °C, using the water bath equipment (Figure 2); the second, in an airtight container at 11 °C in a refrigerator; and the third in a humid room at a temperature of 30 °C. Finally, the temperature sensors were installed and, with help from a Data logger indicator, the records were made during the first thirty hours of age.
The setting was defined according to norms such as the time need, from the beginning of the mechanical kneading, for the penetration of a cylindrical steel needle into cement paste of normal consistency to reach the specified values, both at the start and the end of the setting. This tends to happen in conventional concrete from 50 minutes up to 8 hours (San Juan Barbudo and Chincon Yepes, 2014). However, SC is a hybrid for which, given the activation energy, thixotropy, cohesion, and compaction, the variation of the initial and final setting temperature extends to the first 30 hours, as it approaches ambient temperature. With the records of the temperatures monitored until the first 30 hours, we proceeded to calculate the age factors and equivalent age factor of equations (1) and (2).
It is necessary to clarify that the specified temperature T s corresponds to 22 °C, since it was the temperature at which the samples failed the resilient module test, to which the correlation is to be made.
Resilience Module
However, the maturity of the resistance measured with this method corresponds to the uniaxial load applied during compression. To predict resilience, it was necessary to subject the three mixture designs to the same curing conditions. To this effect, temperature measurements were set for 28 days of age, and then the mixtures were subjected to cyclic loads using the resilient modulus test according the AASTHO T307-99 method (AASHTO, 1999). The results registered a variation in the slope between the ratio of the stress invariant equivalent to the amplitude of the load and the resilient modulus obtained after 100 load applications per cycle. This variation differs between the types of cements and the curing temperatures, as shown in Figure 3.
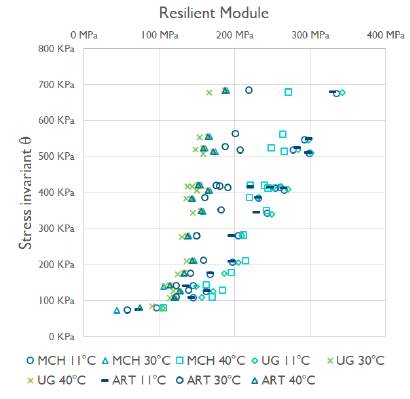
Source: Authors
Figure 3 Relationship between the resilient modulus of the SC cured at different temperatures and the invariant stress.
The way to determine an exact figure for the final resilient modulus was choosing the invariant of the stress, given that the deflection stress is produced by the pavement structure and the overload generated by the passage of the vehicle wheel (Guzman Suarez and Higuera Sandoval, 2016) and, for mixing design purposes, the load corresponds to 4,5 MPa. Thus, with each of the linear trend equations, the corresponding Mr at θ = 450 kPa was calculated for each sample.
The result was tabulated with the most relevant data from the maturity test and with the temperatures recorded during the first thirty hours (Table 2).
Table 2 List of results obtained with the Soil Cement samples cured at different temperatures
| Cement Soil | 𝑇 Ambient | Mr (450 kPa) | Δ𝑇max (30 hours) | Maximum maturity factor | Maximum age factor | Maturity factor x Δ𝑇max | Age factor x Δ𝑇max |
| MCH | 40 | 232,93 | 8,1 | 1,6569 | 41,10 | 13,42 | 332,9 |
| MCH | 30 | 235,64 | 10,1 | 1,2294 | 32,48 | 12,41 | 328,0 |
| MCH | 11 | 255,13 | 12,7 | 1,4250 | 36,63 | 18,09 | 465,2 |
| UG | 40 | 162,00 | 1,6 | 1,6098 | 31,91 | 2,57 | 51,1 |
| UG | 30 | 165,82 | 5,3 | 1,2137 | 23,81 | 6,43 | 126,2 |
| UG | 11 | 272,14 | 15,3 | 1,4250 | 28,31 | 21,80 | 433,2 |
| ART | 40 | 173,62 | 3,1 | 1,6528 | 30,19 | 5,12 | 93,6 |
| ART | 30 | 193,06 | 6,3 | 1,2362 | 32,48 | 7,78 | 204,6 |
| ART | 11 | 280,43 | 11,4 | 1,4250 | 36,63 | 16,24 | 417,5 |
Source: Authors
Prediction Model
To establish a correlation factor, the difference between the maximum and minimum internal temperature was calculated, which, for this work, will be called Temperature Increase (ΔT). And with these results, the maturity factor and the maximum and minimum age factor were recorded for each of the corresponding specimens. Likewise, the following equations were deduced:
where ΔT is the increase in temperature recorded during the first 30 hours of age, Tmax. It is the maximum temperature recorded in °C within the same time interval. t min is the minimum temperature recorded in the same period of time.
After organizing and running relative difference calculation models, it was determined that, due to the increase in temperature ΔT, the most favorable curve is the product between the maximum maturity factor obtained from the temperature measurements during the first 30 hours, for which the Resilient Module (Mr-450) is graphed as a function of the product. It was called 'setting maturity factor' for this investigation, as shown in the Figure 4. In this way, a second equation is in order, which is defined as the following expression:
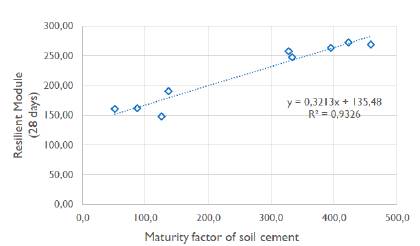
Source: Authors
Figure 4 Relationship between the Maturity Factor and the resilient module at 28 days.
where 𝐹𝑀𝐹 is the setting maturity factor, Δ𝑇 is the temperature increase in C recorded during the first 30 hours of age and calculated from Equation (3), and 𝐹𝑇max is the maximum temperature factor calculated every 0,5 hr for the same time interval using Equation (1).
In the same way, the product is related with the maximum equivalent age factor obtained during the first 30 hours and the temperature increase ΔT, which for this research is called 'setting age factor' as a function of the resilient module. To this effect, the following equation is deduced:
where FE F is the setting maturity factor, ΔT is the temperature increase in °C, and FE max is the maximum age factor calculated in 0,5-hour intervals according to the Arrhenius equation over a period of 30 hours. With the two trends, the prediction equations of the Resilient Modulus of the SC are established as a function of the maximum setting maturity factor and as a function of the maximum setting age factor, with the following equations:
where Mr is the resilient modulus with a stress invariant of 450 kPa at 28 days of age and Fm is the calculated maturity factor of Equation (4) during the first 30 hours.
where Mr is the resilient modulus with a stress invariant of 450 kPa at 28 days, and FE F is the setting age factor, calculated from Equation (5). To verify the prediction model, the line was drawn between the resilient modules calculated from Equations (6) and (7) as a function of the resilient modules measured in the laboratory, as shown in Figure 6 indicating 89,3% as the reliability of the method.
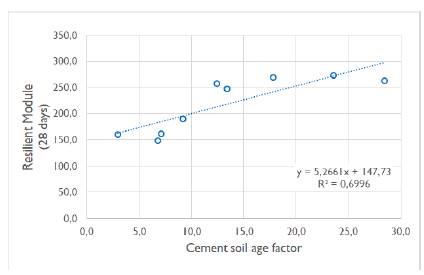
Source: Authors
Figure 5 Relationship between the Age Factor of setting and the Resilient Module at 28 days.
Conclusions
Looking at linear Equation (6), a close proportionality can be found between the increase in temperature during setting with the maturity index and the resilient modulus recorded at 28 days of age.
Comparing the two methods to calculate maturity proposed by ASTM 1079, the one with the highest reliability for predicting the resilient module is the one that uses the maturity factor with 93,26%, while the model that only uses the age factor registers 69,96%.
According to the consolidated results in Table 2, the cement with the lowest Clinker content and added with lime (MCH), registered a similar temperature increase in the three environmental curing conditions, as well as the fact that, in the resilience tests, it was the only mixture that did not register major changes in its results, despite being cured at three different temperatures. This suggests that the ambient temperature does not affect the resilience of the SC-MCH mix, while with the two cements that have the highest Clinker content, the ambient temperature was a variable that directly affected its performance.
The greater the temperature increase recorded during the setting phase of the SC, the greater the resilient modulus at 28 days of age, thus making it a directly proportional variable. In other words, thinking about increasing the temperature in the SC mixture during its construction stage mechanically could bring better results in its performance, as long as it does not reach the point of thermal contraction in the case of cohesive soils. For this reason, it would be recommended to hydrate the material with steam or, if that fails and the tools are not available, to heat the curing water that will spread over the mixture for compaction.
With this method, the possibility of performing a quality control on site through non-destructive tests is available, maintaining the development of multiple reactions and monitoring the evolution of heat through the recording of temperatures that involve the type of cement at room temperature. Consequently, with mobile devices and temperature sensors, its final resistance can be predicted as a pavement structure during the installation of the SC layer. However, this must be validated with different types of soil.

























