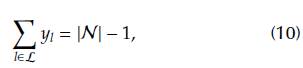Introduction
General context
Electrical distribution networks correspond to the largest part of the power system that is responsible for the commercialization and distribution of electricity services to end-users at medium voltage levels (Sanchez-Zuleta et al., 2012). The extensive longitude of these electrical networks combined with medium voltages is susceptible to high power losses in comparison with transmission networks (Anders, 1994). In the Colombian context, electrical networks typically operate between 11,4 kV and 13,8 kV, with power losses between 6 and 15% of the total energy bought in the spot market (Zuleta et al., 2017). These percentage differences are related to the practices implemented by utilities regarding distribution system operation, as well as to the geographical location of the distribution grid, given that Colombia is essentially a rural country. This implies that the distribution networks have hundreds of kilometers of extension increment power losses due to the natural configuration of the grid (Marneni et al., 2015). An additional fact that furthers power losses in the distribution stage corresponds to the radial structure of this network, which is largely adopted by utilities since it simplifies the coordination of protective devices (reclosers, sectionalizers, and fuses) and also reduces investments in infrastructure such as conductors and supports (Celli et al., 2004; Cruz et al., 2018), among others.
Optimal reconfiguration in distribution networks is a strategy to improve the operating conditions of power systems. It is a real-time operational task performed to minimize losses, improve voltage profiles, improve reliability indicators, balance the load, and minimize operating costs (Celli et al.,, 2004; Cruz et al., 2018).
Network operation and design standards have changed in recent years due to factors such as the need for new monitoring and control systems, the rational use of resources, the demand for high-quality service, and the deregulation of the electric power market (Augugliaro et al., 2004; Azghandi et al., 2021). Each of these factors represents a set of challenges that require technological advances. The aim is to improve the current scenarios and adapt to the challenges of the future energy industry by providing clean, economic, reliable, and safe electrical energy. Optimization applied to distribution networks plays a relevant role in adapting to these new challenges (Jafar-Nowdeh et al., 2020; Vargas-Robayo et al., 2021; Zhengzhong et al., 2021).
Future scenarios for distribution networks need to include strategies that allow operating under unconventional conditions such as dynamic and probabilistic loads, renewable energy sources at distribution points, small-scale generation, bidirectional power flow, among others (Haitham and Helmi, 2021; Jafar-Nowdeh et al., 2020; Raju and Sandeep, 2021). Operation scenarios can be adequately and efficiently addressed by proposing an optimal reconfigurable network (Sambaiah and Jaybarathi, 2021). Motivation
The amount of power losses of distribution networks is undoubtedly an essential issue for electrical distribution companies, since it is the most direct quality indicator in the electrical service (Celli et al., 2004). In order to minimize power losses in distribution networks, multiple strategies can be implemented, such as the optimal placement of distributed generators (Grisales-Norena et al., 2017; Grisales-Norena et al., 2018), shunt-capacitors (Elsheikh et al., 2014, batteries (Grisales-Norena et al., 2019; Montoya et al., 2020b), or the optimal reconfiguration of the network (Verma and Singh, 2018). Nevertheless, in the case of the optimal reconfiguration, most studies focus on the solution technique, glossing over the importance of an adequate mathematical formulation. This gap in the literature is the main motivation of this research. Our interest is to provide a correct mathematical formulation of the reconfiguration problem in distribution networks using a mixed-integer nonlinear programming model that can be solved with any optimization package (Montoya et al., 2020a). This is especially important since engineers need to be formed in mathematical analysis, i.e., with the capabilities of current adequate mathematical models that represent real-life problems. Moreover, they need to have the ability to solve them efficiently.
State of the art
The problem of the optimal reconfiguration of AC distribution feeders is a classical optimization problem in power systems analysis (Civanlar et al., 1988). In general terms, this problem can be described as determining the best subset of lines that generates a radial configuration network from an initial solution space conformed by connected (existing) and tie lines (opened), which allows reducing the total active power losses into the network, fulfilling the devices' capabilities (current in lines and power generation in sources) and guaranteeing power balance and voltages bounds in all the nodes. In mathematical terms, this problem can be formulated by using a mixed-integer nonlinear programming structure, i.e., an MINLP model (Lavorato et al., 2012). To solve this problem, the specialized literature has proposed multiple approaches, most of them based on metaheuristic optimization, namely genetic algorithms (Su et al., 2005; Zhang etal., 2014), ant colony optimization (Ahuja and Pahwa, 2005; Su et al., 2005), chaotic stochastic fractal search algorithms (The et al., 2020), tabu search algorithms (García-Martínez and Espinosa-Juarez, 2013), binary particle swarm optimization (Arya et al., 2011; Tandon and Saxena, 2014; Xiaozhi etal., 2010), culture search algorithms (Verma and Singh, 2018), ant lion optimizer (Shokouhi et al., 2017), and bat algorithms (Quintero-Duran et al., 2019), among others.
The main characteristic of the aforementioned metaheuristic optimization approaches is that all of them concentrate efforts on solving the reconfiguration problem in sequential steps by proposing codification and evolution strategies. This implies that they have decomposed the problem into a master-slave strategy, where the metaheuristic approach is the master layer, and the slave stage corresponds to a conventional power flow approach (Su et al.,2005). Even if these strategies are efficient to solve complex optimization problems implying binary variables (Verma and Singh, 2018), they have a recurrent problem from a theoretical perspective, since these neglect the importance of a correct mathematical representation of the problem and only focus on designing an algorithm to solve it (Grisales-Norena et al., 2018). To address the problem of reconfiguration correctly, Lavorato et al. (2012) presented a complete formulation to solve the problem regarding the optimal planning of distribution network systems that can be solved in the AMPL software. Nevertheless, the problem in that formulation is the representation of the voltage profiles, since the authors follow the classical representation that uses trigonometric functions, which clearly includes strong nonlinearities in the optimization model, thus increasing the possibilities of staying stuck in a local solution (Montoya et al., 2020; Sultana and Roy, 2015). Hence, we present an alternative mathematical formulation to address this problem, which allows representing the problem of the optimal reconfiguration in AC distribution networks without involving trigonometric functions (which is presented as a tutorial). This approach will be particularly interesting to introduce beginners to optimization problems, especially for power systems engineers (Soroudi, 2017).
Contributions and scope
The main contributions of this research can be summarized as follows:
√ The mathematical formulation of the optimal reconfiguration problem in AC distribution networks using a rectangular representation of the voltage and current variables added to the inclusion of binary variables, which allows determining the subset of conductors needed to minimize the total power losses in all the branches of the network.
√ The implementation of the proposed MINLP formulation in a specialized software known as the general algebraic modeling system (GAMS) in the form of a tutorial that allows introducing engineering students to mathematical optimization.
It is worth mentioning that the proposed MINLP model for optimal reconfiguration of AC distribution feeders has not been previously reported in the specialized literature, which corresponds to a gap that this research aims to fill. In addition, we introduce the general algebraic modeling system as a powerful optimization tool that helps solve large-scale nonlinear programming problems by focusing on the mathematical formulation and not on the solution technique. This is important since, in power systems optimization, when metaheuristic optimization is employed, the mathematical model is neglected by tackling the sequential step to solve the optimization problem. This practice is not advised when engineering students are introduced to mathematical optimization; the main focus must be the correct formulation of the problem under study and not the solution method. Therefore, this research concentrates on presenting a comprehensive formulation of the optimization reconfiguration of AC distribution feeders using an MINLP model.
Organization of the document
This paper is organized as follows: the MINLP formulation section presents the mathematical formulation of the optimal reconfiguration problem of AC distribution feeders by using a rectangular representation of the voltage and current variables, which produces a mixed-integer nonlinear programming model. The next section introduces the solution methodology based on the general algebraic modeling system that allows implementing the MINLP model in a compact structure. The numerical validation section presents numerical simulations for a classical 13-node test feeder using the GAMS software, as well as their comparisons with literature reports. The conclusions and future Work section presents the principal outcomes derived from this work, as well as some possible future developments.
MINLP formulation
The problem of the optimal reconfiguration of electrical distribution networks is indeed a complex optimization problem due to the presence of the power balance equations containing multiple products between voltage and currents (nonlinear expressions). Additionally, the nature of this optimization problem is binary, given the necessity of selecting a subset of conductors that minimizes the power losses of the distribution system for a particular load condition. The complete mathematical model of the reconfiguration problem in distribution networks is described below.
Objective function
The objective function of the optimal reconfiguration problem corresponds to the minimization of the active power losses in all the branches of the network ploss, as expressed by Equation (1).
where R l ; is the resistance value of the conductor associated to branch l, and l is the magnitude of the current that flows in said branch. Note that ℒ is the set containing all the branches (connected and non-connected).
Set of constraints
The set of constraints that defines the solution space of the optimal reconfiguration problem in AC distribution networks is defined as follows: first, the active and reactive power balance equations are presented using the real and imaginary parts of the voltage and current variables, as shown in Equations (2) and (3).
where Pk
⅋ and Pk
d are the active power generation and demands at node k, respectively; Qk
⅋ and Qk
d represent the reactive power generation and consumption at node k, respectively; Vr
k and Vi
k are the real and imaginary parts of the voltage variable at node k; and Ir
l and Ii
l correspond to the real and imaginary components of the current that flows in branch l. Note that
 is the incidence node-to-branch matrix, and its components are defined as follows:
is the incidence node-to-branch matrix, and its components are defined as follows:
√
 = +1 if the branch Z is connected at node k and the current I; leaves this node.
= +1 if the branch Z is connected at node k and the current I; leaves this node.
√
 = -1 if the branch ; is connected at node k and the current I; arrives to this node.
= -1 if the branch ; is connected at node k and the current I; arrives to this node.
√
 = 0 if the branch ; is non connected at node k.
= 0 if the branch ; is non connected at node k.
Second, the real and imaginary currents are defined as function of the voltage drops at the ends of each branch (Equations (4) and (5)).
where y; is a binary variable that determines whether the branch ; is connected to the distribution network (y l = 1) or not (y l = 0) and X; is the reactance effect in the conductor l. Note that N is the set that contains all the nodes of the network.
Third, the magnitudes of the voltages and currents are defined through Equations (6) and (7).
Fourth, the current capabilities and voltage regulation bounds are defined to ensure the useful life of the conductors and the regulatory policies regarding maximum voltage deviations (Equations (8) and (9)).
where I l max represents the maximum thermal limit of the conductor associated with branch l, and Vk min and Vk min represent the minimum and maximum voltage bounds allowed in all the nodes of the network.
Fifth, to ensure that the resulting configuration of the distribution network is radial, a constraint is imposed in the number of conductors that can be connected to the distribution (Equation (10)).
where |N| represents the cardinality of the set of nodes, i.e., the number of elements in this set.
The interpretation of the mathematical model in Equations 1) to (10) that represents the problem of the optimal reconfiguration of AC distribution networks has the following description: Equation (1) corresponds to the objective function associated with the power losses minimization in all the branches of the network. Equations (2) and (3) determine the active and reactive power balance in all the nodes of the network. These Equations are widely-known in the specialized literature as power flow constraints. Equations (4) and (5) calculate the real and imaginary components of the currents that flow at each branch. Equations (6) and (7) determine the magnitude of the network variables, i.e., voltages in all the nodes and currents in all the branches. Equations (8) and (9) allow for solutions that fulfill the thermal capabilities of the calibers associated with each branch and the voltage regulation bounds permitted in all the nodes. Finally, Equation (10) defines that the number of branches that can be connected produces aradial configuration. Nevertheless, this radial structure is ensured by the presence of the active and reactive power balance equations in the mathematical model, i.e.,Equations (2) and (3) and the number of conductors available for operation, i.e., constraint (10).
Remark 1. The mathematical formulation presented inEquations (1)to (10) is not unique, since multiple representations can be reached by representing the real and imaginary parts of the currents as a combination of magnitudes and angles, i.e., trigonometric functions. However, these trigonometric functions introduce complex nonlinearities that can make the solution to the problem difficult.
Solution methodology: GAMS software
This section presents the optimization strategy adopted to solve the problem of the optimal reconfiguration of AC networks with an MINLP model described in Equations (1) to (10). To this effect, the general algebraic modeling system is used as a solution technique. The GAMS software is a powerful tool that allows solving complex optimization models including linear and mixed-integer programming, quadratic programming and general nonlinear programming models with mixed variables (i.e., binary, integer) (Soroudi,2017).
In the specialized literature, GAMS has been employed to solve complex optimization problems such as the optimal selection of conductors in distribution networks (Montoya et al., 2018), optimal planning of transmission networks (Aguado et al., 2017), optimal location of renewable generation in distribution networks (Babu and Singh, 2016; Gil-Gonzalez et al., 2020; Montoya et al., 2020a), optimal operation of power systems with batteries (Soroudi, 2017; Montoya et al., 2020c), optimal design, and sizing of a pressure retarded osmosis power plant (Naghiloo et al., 2015), voltage stability analysis in direct current networks (Amin etal., 2019), multi-objective optimization of the stack of a thermoacoustic engine (Tartibu et al., 2015), multi-objective optimization of energy and water management in networked hubs (Pakdel et al., 2020), the optimal location of protective devices (Izadi et al., 2019; Gallego-Londono et al., 2016), and so on.
The main advantages of using the GAMS software in mathematical optimization can be summarized as follows (Montoya et al., 2020c; Soroudi, 2017; Vargas-Robayo et al., 2021):
√ It works with a compact structure, i.e., it employs sets that contain information regarding the number of variables as well as the dimension of the solution space.
√ The information related to the system is introduced by using matrices, vectors, and scalars, and these can be assigned to the set's domain.
√ It uses a symbolic representation of the variables to mathematically represent the optimization model under study, with the characteristic that the model has a pretty similar structure as presented in Equations (1) to (10).
√ It is possible to differentiate the nature of the variables that intervene in the mathematical model, i.e., discrete(integer), binary, continuous, and positive variables, among others.
√ Multiple solution techniques based on interior point and branch and bounds methods can be selected to resolve the mathematical optimization model. Some of the classical natures of problems are linear programming (LP), nonlinear programming (NLP), mixed-integer programming (MIP), and mixed-integer nonlinear programming (MINLP).
Figure 1 presents the flowchart for the implementation of optimal reconfiguration in radial distribution networks using MINLP through GAMS. To illustrate an implementation of a mathematical model using the GAMS software, let us consider a small optimization example consisting of an AC distribution network operated at 13,2 kV with 5 nodes, 4 built lines, and 3 tie lines. The electrical configuration is depicted in Figure 2. The initial power losses in this system with the configuration depicted in said Figure are 222,842 kW, and the minimum voltage profile occurs in node 5 with a value of 0,952 pu.
The load information of this test feeder is reported in Table 1, and the branch data including connected and tie lines are presented in Table 2.
It is worth mentioning that lines e, f, and g represent the subset of possible links to reconfigure the AC distribution system by always guaranteeing a radial topology. In addition, the incidence node-to-branch matrix that represents this test feeder has the following structure:
where it was assumed that the currents flow from the smallest to the highest by rearranging the columns from lines a to g and the rows from node 1 to node 5.
The implementation of the mathematical model from Equations (1) to (10) to solve the reconfiguration problem in AC networks using GAMS is presented in Algorithm 1. Note that 13,2 kV and 1 000 kVA are used to obtain a per-unit (pu) representation of the system.
The information in Algorithm 1 can interpreted as follows:
√ Lines 1 to 5 determine the sets in the optimization problems, i.e., nodes, lines, and generators, including the map that defines the location of the slack source.
√ Lines 6 to 31 define all the constant information related to the test feeder, i.e., voltage ranges, and branch and load parameters.
√ Lines 32 to 44 define the variables of the problem, i.e., voltages, currents, active and reactive power generations, and binary variables, as well as their constant bounds.
√ Lines 45 to 61 are the necessary equations to solve the problem, starting by their names and followed by their mathematical structures.
√ Lines 62 to 64 present the solution of the problem by defining its nature and selecting the minimization strategy. In addition, the variables of interest are extracted to analyze the final solution.
The solver used to reach the optimal solution of the AC reconfiguration problem in the 5-node test feeder corresponds to the DICOPT taking an average processing time of 1,40 s, which is fastest than any heuristic optimization approach. Figure 3 reports the final solution reached by GAMS, where lines d and f have been disconnected, and lines c and e are introduced in the final solution. The last power losses are 124,420 kW, which implies a reduction of about 44,17% regarding the base case.
It is important to mention that the implementation reported in Algorithm 1 can be applied to any AC distribution networks, regardless of the number of nodes and candidate lines, since it presents a compact structure for optimization, which is one of the most important and largely-known advantages of the GAMS software (Soroudi, 2017).
Numerical validation
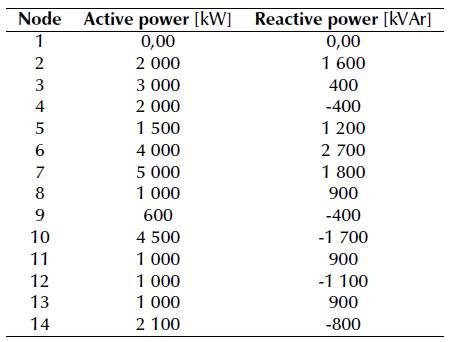
In this section, in order to demonstrate the efficiency of the proposed approach for the optimal reconfiguration of AC distribution systems, the classical medium voltage distribution network composed by 14-nodes and 16 lines reported in (Tapia-Juarez and Espinosa-Juarez, 2013) is employed (Figure 4). This system is operated at 23 kV, and the based power is assumed to be 1 000 kVA. The initial active power losses for this test feeder are 512,165 kW. The information on the connected and candidate branches is reported in Table 3, and the load information is listed in Table 4.
In this test system, we evaluate three simulation cases as follows:
√ Scenario 1 (S1): The reconfiguration of this test feeder considering that all the tie lines are initially disconnected.
√ Scenario 2 (S2): The reconfiguration of this test feeder considering the presence of a distributed generator at node 8 with a capacity of 10 MW operated with unity power factor.
√ Scenario 3 (S3): The reconfiguration of this test feeder considering the presence of a large-scale capacitor compensation at node 6 with a size of 6 MVAr.
Note that the first simulation scenario is the typical simulation case explored in the specialized literature for the optimal reconfiguration of the 14-node test feeder using metaheuristic techniques (Verma and Singh, 2018).
Table 5 presents the solution of the reconfiguration problem in the 14-node test feeder considering S1, where GA means genetic algorithm (Su et al., 2005), ACSA means ant colony search algorithm (Su et al., 2005), GAST means genetic algorithms based on spanning trees (Zhang et al., 2014), and MCA means modified culture algorithm (Verma and Singh, 2018). It is worth mentioning that Verma and Singh (2018) claim an optimal value of about 462 kW regarding power losses. However, this is not possible for this system, since, when we evaluated their solution, it turned out to be 466,47 kW.

Source: Authors
Figure 5 Voltage behavior in the nodes of the 14-node test feeder for each one of the simulation scenarios: (a) S1, (b) S2, and (c) S3
From the results in Table 5, we can note the following. i) All the comparative methodologies, as well as the proposed MINLP model, solved in GAMS reach the same optimal solution (466,467 kW), which corresponds to a reduction of about 8,89% with respect to the base case. ii) Of the methods identified in the state of the art for the comparative analysis, none recorded the total calculation time. The state of the art was reviewed according to this work's contribution, objective, and motivation. It is relevant to highlight that the methods studied in this research are not the only strategies available for the optimal reconfiguration of radial networks. Therefore, it is likely that other solution methods do include runtime analysis. In the case of the proposed approach, this takes about 11,560 s, which is a short time for solving MINLP models. This is important since the utility can make multiple simulations before making a final decision regarding investment and grid intervention. iii) The solution reached by the GAMS package is obtained by using an interior-point optimization method combined with the branch and bound strategy, which makes it efficient in terms of quality response and computational effort (Kaur et al., 2014; Montoya et al., 2020c).
In the case of S2, the initial power losses considering the operation of the distributed generator with 10 MW with the initial topology of the system presented in Figure 4 are 364,057 kW. Once the mathematical formulation is solved by the GAMS package, the final power losses are 339, 133 kW, which implies an improvement regarding power losses of about 24,924 kW. To reach this solution, the set of the disconnected lines are {4 - 5, 7 - 9, 11 - 12}, which is a solution found in approximately 15,50 s. This implies that the presence of the distributed generator does not significantly affect the complexity of the optimization problem under study in terms of the processing times.
As for S3, the initial power losses considering the initial topology depicted in Figure 4 and a capacitive compensation of 6 MVAr at node 6 are 500, 697. Once the proposed methodology for optimal reconfiguration in AC networks is solved through GAMS, the resulting power losses are 463,039 kW, which means a reduction of 7,52% with respect to the initial case. Note that the disconnected lines are {6 - 8, 7 - 9, 5 - 14}, which agrees with the optimal solution for S1. In this problem, the GAMS package takes about 6 s to find the optimal solution, which confirms its effectiveness at analyzing complexMINLP models (Soroudi, 2017).
Remark 2. Note that the punctual injection of active and reactive power in specific nodes significantly influences the power loss behavior of the network, as it can be observed in the initial cases of S2 and S3. However, the reconfiguration strategy applied to the test system considering these distributed energy resources can also help mitigate the negative effects produced by excessive injections of active and reactive power into the grid.
Figure 5 reports the voltage profiles for the 14-node test feeder in all the simulation scenarios including their base cases.
From Figure 5, we can observe that i) the reconfiguration of the AC distribution network allows improving the average voltages in all the nodes of the system, given that the reduction of power losses translates into lower voltage drops. Nevertheless, this does not imply that the worst voltage profile will improve, since the mathematical model presented in this paper is strongly nonlinear and non-convex, as seen in Figure 5b. ii) The presence of distributed generation and/or capacitor banks has a higher impact on the voltage profiles of the network (compare Figures 5b and 5c with 5a), which is expected in distribution networks since these largely modify the total power injection in the substation, whereas reconfiguration only redistributes those fluxes in a better way, regardless of the presence of shunt elements, i.e., distributed generators and/or capacitor banks. iii) The reconfiguration of the network has positive impacts since it allows for further reduction in power losses, thus making it attractive for utilities regarding power quality and regulatory benefits via billing, as is the case of Colombian companies (Sanchez-Zuleta et al.,2017).
Remark 3. The effect of current constraints (6) and (8) can be considered for optimal reconfiguration in AC distribution networks if there is information available regarding the maximum thermal capabilities of the existing and tie lines, since the proposed rectangular representation of this problem allows evaluating it easily, due to the fact that our model is defined as a function of the branch currents, which implies that the information of the current magnitudes in all the branches is always available.
In order to provide enough information to analyze the current flows in the 14-node test feeder, Table 6 presents the current magnitudes in this test system for each of the simulation scenarios.
From the results in Table 6, we can observe that each one of the reconfiguration planes provided by each simulation scenario effectively helps to redistribute the current flow in all the lines, which is directly connected to the power loss improvement. For example, in S1, if its supposed that lines 1 -6 have a current rate of 700 A, then, its loadability is about 98,95% in the initial case. Nevertheless, after the application of the reconfiguration strategy, the final loadability is about 88,03%, implying a liberation of capability of 10%, which can be used in the case of loads attended by this line that report increments in the near future. However, the discharge in this distribution line implies a loadability increment in some other lines to guarantee that the amount of power provided to the loads is satisfied. However, these increments in some lines are not a negative effect, since the global behavior of the network demonstrates that the power losses are reduced. This behavior is attributable to the nonlinear properties of the optimization problem analyzed in this research. Note that similar analyses can be made for S2 and S3 regarding their base cases.
Conclusions and future work
This paper proposes a new mathematical formulation to model the problem of the optimal reconfiguration of AC distribution feeders based on a rectangular representation of the voltage and current variables in nodes and branches, respectively. Due to the nature of the MINLP model's results, the GAMS package was selected as solution methodology since the main focus of this paper was indeed the mathematical formulation, not the solution technique. We presented the methodology in the style of a tutorial to help engineering students understand the real complexity of the reconfiguration problem in AC distribution feeders.
The numerical results in the case under study (14-node test feeder) for all the simulation scenarios demonstrated that the reconfiguration of the system (modification of the topology) has positive impacts regarding power losses minimization, regardless of the presence of distributed energy resources in the grid, i.e., distributed generators and/or capacitor banks. This implies that the proposed approach is suitable to be extended to electrical distribution networks with batteries and economic dispatch multi-period environments.
There is an alternative way to represent the reconfiguration problem in AC networks by using the magnitude of the nodal voltages and their angles. Nevertheless, that approach introduces complex characteristics in the model concerning trigonometric functions that relate voltages and currents in the power balance constraints. Said approach is less efficient than the rectangular representation proposed in this paper. It can multiply the possibilities of getting stuck in the local optimums, primarily when packages such as GAMS are used as solution methodology.
This work analyzes the problem of optimal reconfiguration in distribution networks using variables as electrical parameters, specifically power, voltage, and current. As future work, in the area of optimization for power systems, several variables can be implemented in the objective function and the constraints model. Likewise, criteria associated with social impacts can be included, thus allowing to analyze how the reconfiguration of networks, the inclusion of renewable energy sources, the implementation of storage systems, and others contribute to sustainable development.