ARTÍCULO ORIGINAL

Modelado de curvas de ruptura en la adsorción de agua sobre sílica gel y zeolita 4A

Modelling of breakthrough curve in water adsorption on silica gel and zeolite 4A

Andrés Rivera Guerrero, Pedro Bejarano Jiménez, Gerardo Rodríguez Niño^*.

Grupo de Investigación en Procesos Químicos y Bioquímicos, Departamento de Ingeniería Química y Ambiental, Universidad Nacional de Colombia - Sede Bogotá. Cra. 30 No. 45-03. Bogotá, Colombia.

^*Autor de correspondencia: teléfono:+ 57 + 1 + 3165000 ext. 14302, correo electrónico: grodriguezn@unal.edu.co (G. Rodríguez)

(Recibido el 22 de mayo de 2013. Aceptado el 31 de enero de 2014)

Resumen

Este artículo presenta el desarrollo de un modelo computacional para simular la adsorción de agua en un lecho empacado, comparando el desempeño de una zeolita 4A y una sílica gel tipo 'A'. Se usó una variación de la isoterma de Langmuir para la zeolita 4A y la isoterma de Tóth para la sílica gel; se utilizó el modelo de fuerza motriz lineal (LDF) para la velocidad de adsorción, con un coeficiente total dependiente de la temperatura. El modelo está constituido por cinco ecuaciones diferenciales parciales asociadas con las variables: fracción molar de agua, temperatura, presión, velocidad superficial y carga adsorbida de agua. Para resolver el sistema se empleó el método de líneas (MOL) con el integrador ODE15S de Matlab^®. Se evaluaron como variables de respuesta el intervalo de tiempo característico de la curva de ruptura, la asimetría, la temperatura máxima y la caída de presión, mediante un esquema factorial de dos niveles. El tipo de adsorbente es la variable que más influencia tiene en las variables de respuesta. A la zeolita corresponde la mayor velocidad de adsorción, comportamiento que puede explicarse si se observa la forma de su isoterma de adsorción, aunque presenta una menor capacidad de retención de agua y mayor resistencia a la transferencia de masa.

Palabras clave: Adsorción de agua, simulación, isoterma de adsorción, curva de ruptura, adsorbentes, lecho empacado

Abstract

This paper presents the development of a computational model to simulate the adsorption of water in a fixed bed, comparing the performance of zeolite 4A and silica gel type 'A'. A variation of the Langmuir isotherm for zeolite 4A and Tóth isotherm for the silica gel were used; Linear Driving Force (LDF) model was used for adsorption rate with an overall coefficient temperature dependent. The model is composed of five partial differentlal equatlons assoclated with mole fraction of water, temperature, pressure, superficial velocity and water loading. Method of lines (MOL) was used with the function ODE15S of Matlab^® to solve the system. As response variables the characteristic time interval of the breakthrough curve, asymmetry, maximum temperature and pressure drop, through a two-level factorial scheme were evaluated. Adsorbent was the most influential variable on the response variables. Zeolite has the highest rate of adsorption due to the shape of the adsorption isotherm, but has a lower water retention loading and increased resistance to mass transfer.

keywords:Water adsorption, simulation, adsorption isotherm, breakthrough curve, adsorbents, fixed bed

Introducción

La adsorción es una operación ampliamente empleada en procesos en los que es necesario retirar agua de algunas corrientes de interés industrial, por considerarla un componente no deseado; por ejemplo: la obtención de alcohol carburante [1], la separación de aire [2, 3] y los tratamientos de gas natural [2], gas de síntesis, gases inertes, reciclo de reformado de hidrógeno y corrientes de craqueo [4]. Cabe precisar que el adsorbente debe elegirse cuidadosamente, de acuerdo con las necesidades del proceso. Cuando el contenido final de agua no es crítico, es común emplear sílica gel; si la humedad final debe controlarse de manera estricta, con frecuencia se utilizan zeolitas; sin embargo, en algunos sistemas se combinan estos dos adsorbentes: la sílica retira la mayor cantidad de agua y la zeolita el exceso respecto al contenido final establecido [2].

Anteriores investigadores [5] realizaron estudios cinéticos y de equilibrio sobre el desempeño de diversos materiales frente a la adsorción de agua. Para el análisis emplearon un modelo isotérmico y compararon una zeolita, un carbón activado y una alúmina activa. Concluyeron que a bajas concentraciones de agua la zeolita tiene mayor capacidad de adsorción, pero cerca a la saturación la capacidad de la alúmina es mayor; no obstante, la difusividad del agua en la estructura de la zeolita es menor y, por lo tanto, presenta mayor resistencia a la transferencia de masa.

En la actualidad, los modelos computacionales son herramientas importantes para el diseño de operaciones industriales ya que minimizan el tiempo y los costos que requieren los estudios piloto. Estos modelos también son la base para la optimización que se requiere en la búsqueda de reducir costos y aumentar los márgenes de ganancia de las empresas.

El objetivo de este trabaj o es mostrar cómo un modelo computacional, basado en datos de fácil acceso, puede utilizarse como una herramienta para el diseño preliminar de un sistema de deshidratación, dado que no sólo permite evaluar de diversos adsorbentes, sino los efectos sobre el desarrollo de la operación de variables como presión, temperatura y fracción de agua alimentada.

Metodología

El análisis de las curvas de ruptura se realizó mediante simulación numérica, para lo cual se caracterizó el comportamiento de los adsorbentes con información de trabajos previos [6-9]. Se analizó la operación de deshidratación de aire (corriente inerte) en un lecho empacado, a escala laboratorio, esquema comúnmente usado para estudios de curvas de ruptura [7, 10, 11]. Se utilizó un diseño de experimentos factorial de dos niveles, en el que se evaluaron y compararon parámetros de la curva de ruptura como el intervalo de tiempo característico, la asimetría, la temperatura y la caída de presión máximas.

Ya que los ensayos corresponden a simulaciones no se requieren réplicas y se considera que la desviación estándar es cero.

Adsorbentes

Se eligieron como adsorbentes una zeolita 4A y una sílica gel tipo 'A', que son usados en operaciones de deshidratación [2, 12]. En la tabla 1 se relacionan los datos de caracterización física de los adsorbentes.

Para realizar el análisis del contenido de agua de la corriente gaseosa tratada se usó la fracción molar de agua y la humedad relativa. La humedad relativa se calculó mediante la ecuación (1):

Pw (Pa) es la presión parcial de agua, P^sw (Pa) la presión de saturación de agua a la misma temperatura de la corriente, y H la humedad relativa. Para calcular la presión de vapor del agua [13] se empleó el modelo de Antoine modificado, como se muestra en la ecuación (2):

T(K) es la temperatura de trabajo y los parámetros a^s, b^s(K) y c^s(K) son las constantes de Antoine. Los parámetros para el agua se encuentran en la tabla 2.

Para modelar la isoterma de adsorción de agua en zeolita se usó un modelo [7] basado en una modificación de la isoterma de Langmuir, para una muestra comercial de la empresa Grace Davison. El modelo y la dependencia de los parámetros con la temperatura se muestran en las ecuaciones (3) a (5).

y q⁰w (mol/kg) son parámetros característicos del par adsorbente-agua; T₀ (K) es una temperatura de referencia, q^sw (mol/ kg) la carga máxima adsorbida a la temperatura de trabajo y q^*w (mol/kg) la carga en equilibrio a la temperatura y presión parcial de trabajo. Los valores empleados se reportan en la tabla 3.

Para el caso de la sílica gel tipo 'A' se empleó el modelo de Tóth, que fue validado para una muestra de Fuji Davison [9] y se muestra en las ecuaciones (6) y (7).

b_t (Pa^-1), b_t,0 (Pa^-1) y t_T son parámetros característicos del par y R (J/mol K) es la constante universal de los gases. Los valores empleados se muestran en la tabla 4.

El modelo de fuerzamotriz lineal (LDF), ampliamente usado para operaciones de adsorción, se empleó para representar la cinética [14]. Si se considera que la principal resistencia a la transferencia de masa se presenta en el interior de las partículas, el coeficiente global se relaciona directamente con la difusividad del agua en el adsorbente. La ecuación (8) muestra la forma empleada para calcular el coeficiente de transferencia, donde sólo se considera la dependencia con la temperatura [6, 8].

(m²/s) es la difusividad intrapartícula de referencia, E_c (J/mol) la energía de activación, R_p(m) el radio de las partículas y k_LDF (s^-1) el coeficiente global de transferencia. En la tabla 5 se encuentran los valores empleados.

Las propiedades termodinámicas y de transporte, que se presentan en la tabla 6, fueron estimadas con base en las propiedades del aire estándar, a 300K y 1bar.

Modelo diferencial

Se empleó un modelo diferencial unidimensional, para el volumen de control mostrado en la figura 1 , que se considera como un lecho fijo con paredes impermeables, pero que permite un intercambio de energía con un medio refrigerante exterior.

La fase gaseosa se considera ideal y su concentración se calculó con la ecuación (9):

c (mol/m³) es la concentración molar de la fase vapor y P (Pa) la presión total. La cinética de adsorción se representa con la ecuación (10):

q_w (mol/kg) es la carga actual adsorbida. Para el balance de agua se emplea la fracción molar como variable principal y se tienen en cuenta los efectos de la difusión axial, ecuación (11).

y_w es la fracción molar de agua, (m²/s) la difusividad axial efectiva y v_s (m/s) la velocidad superficial. La difusión axial se calcula mediante la ecuación (12), correlación empleada para sistemas de adsorción [2, 11].

es el número de Reynolds y Sc es el número de Schmidt. Los efectos térmicos se tienen en cuenta con un modelo pseudohomogéneo, en el que se asume que el sólido está en equilibrio térmico con la fase gaseosa en cada punto del lecho; también se considera un término asociado con la transferencia de energía hacia un medio externo, así como la dispersión axial. El balance se presenta en la ecuación (13):

p_g(kg/m³) es la densidad de la fase vapor, U (W/ m²•K) el coeficiente global de transferencia de calor al exterior, D (m) el diámetro del lecho, que se fijó en 0,01 y T_ref (K) la temperatura del refrigerante. Para tener en cuenta los efectos de difusión térmica axial se empleó la ecuación (14) [2, 11].

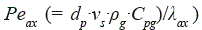es el número de Peclet axial y es el número de Prantl.

La variación de velocidad producida por el material adsorbido, los gradientes de presión y la temperatura se tienen en cuenta a partir del balance total de materia en la ecuación (15):

La caída de presión por el flujo a través de un medio poroso se consideró por medio de la ecuación de Ergun [2], en la forma de la ecuación (16):

El tiempo estequiométrico de saturación, tiempo requerido para saturar el lecho en ausencia de resistencia a la transferencia de masa, se tomó como parámetro para cada simulación y se calculó con la ecuación (17):

L (m) es la longitud total del lecho empacado, fijada en 0,5. En la tabla 7 se resumen las condiciones de frontera y en la tabla 8 las condiciones iniciales. Para la presurización se considera un perfil lineal en la entrada del lecho, desde la presión atmosférica normal hasta la de operación; esta etapa dura 9s, en todos los casos, seguida por otra de 1s a la presión de adsorción. La velocidad de alimentación de la fase vapor siempre es 0,3 m/s, por debajo del límite que da lugar a erosión excesiva del adsorbente [2].

Los subíndices ƒ i y pre se refieren a las condiciones de alimentación, iniciales y final de la presurización, respectivamente.

Diseño experimental

Ya que muchos investigadores están familiarizados con el análisis de sistemas mediante el enfoque de efectos por medio de experimentos factoriales, se empleó este esquema, con dos niveles, donde cada ensayo fue simulado en computadora. Con este procedimiento, la información contenida en el sistema de ecuaciones diferenciales se convierte en resultados visibles que se muestran más adelante en las figuras 5 a 8. Se analizaron como variables de respuesta el intervalo de tiempo característico, la asimetría, la temperatura y la caída de presión máximas.

Se exploró el efecto de cuatro variables: temperatura, presión, humedad relativa del alimento y coeficiente de transferencia de calor; este último estimado a partir trabajos de adsorción en lechos empacados, a escala laboratorio [10, 11]. Cada simulación se identificó con un código compuesto por una letra (adsorbente) y cuatro dígitos que, siguiendo el orden de las variables de la tabla 9, permiten identificar el nivel de la variable utilizado.

Por ejemplo, el experimento Z0111 corresponde al uso de la zeolita 4A con temperatura de 323K, humedad de 75%, presión de 250000Pa y coeficiente de transferencia de calor de 50W/m²K. Para realizar un análisis global se emplearon variables adimensionales. En las ecuaciones (18) y (19) se muestra la relación para obtener el tiempo y la distancia adimensionales.

t_c representa el tiempo característico de la operación; bien sea en la etapa de presurización o de adsorción. El intervalo de tiempo característico, asociado con la zona de transferencia de masa (mass transfer zone, MTZ [2]) y la asimetría se calcularon con las ecuaciones (20) y (21):

En estas ecuaciones se emplean los tiempos adimensionales necesarios para detectar una concentración de agua en el producto correspondiente al 10, 50 y 90% del contenido inicial (θ_10%,θ_50% y θ_90%).

Método numérico

El sistema, constituido por cinco ecuaciones diferenciales parciales, presenta complejidad para su integración por su alta no linealidad. Se ha mostrado [16] que el método de líneas (MOL) es útil y más eficiente que otros para resolver modelos de adsorción, razón por la cual fue elegido para el presente trabajo. Como el sistema presenta un marcado carácter hiperbólico, se empleó una discretización ''upwina'' para la primera derivada y un modelo centrado para la segunda derivada [17] y se empleó la función ODE15S, incluido en el software Matlab^®, para integrar el sistema discretizado.

Con el propósito de facilitar la integración del modelo se usó la aproximación presentada en la ecuación (22) [1]:

f(y) es la matriz de coeficientes variables y F(y) representa el operador diferencial. Así se genera un sistema con coeficientes semiconstantes con el fin de reducir el tiempo de cálculo. El modelo se ejecutó con el software MATLAB R2012a de 32bits, en una computadora personal con un procesador de 1,6GHz y 2GB de memoria RAM.

Resultados

Los resultados obtenidos en la simulación se usaron para realizar un análisis de efectos estandarizados, a fin de cuantificar y comparar la influencia de cada variable en el comportamiento de las curvas de ruptura. Los perfiles de variables como fracción molar, carga adsorbida, temperatura y velocidad se emplearon para comparar los dos adsorbentes.

La distribución del tamaño de poro tiene gran influencia en las propiedades de los adsorbentes, con respecto a su isoterma de adsorción y a la facilidad de difusión de las moléculas en su estructura. La sílica gel es un adsorbente con una amplia distribución de tamaño de poro, generalmente mayor que 20Å; en contraste, las zeolitas tienen una estructura cristalina, con una estrecha distribución de tamaños de poro (tamices moleculares). La zeolita 4A, utilizada en este trabajo, tiene la mayoría de poros con diámetro de 4Å [12]. En la figura 2 se observan las isotermas de los adsorbentes empleados. La zeolita se satura a bajas humedades, debido al llenado de los microporos [2].

Otro efecto de la distribución del tamaño de poro se observa en la figura 3. Menores diámetros de poro implican una mayor resistencia a la difusión de agua en la estructura y, por ende, un menor coeficiente global de transferencia.

En las 32 simulaciones realizadas se observó que la composición, la carga y la temperatura del lecho durante la presurización no cambian en forma apreciable. En la figura 4 se muestran los perfiles de presión y velocidad obtenidos para el ensayo Z0001, en la que se observa que el valor final de la presión se alcanza en un corto tiempo.

La mayor velocidad conseguida durante la presurización, en las simulaciones, fue de 0,05m/s, bastante inferior a la velocidad de alimentación en la adsorción (0,3 m/s). La máxima velocidad se alcanzó en los primeros instantes y en la entrada del lecho, donde el gradiente de presión es máximo.

En la figura 5 se muestra el diagrama de Pareto correspondiente a los efectos sobre el intervalo de tiempo característico. Esta variable expresa la desviación de la operación sin resistencia a la transferencia de masa, comparada con el comportamiento real [2]. A mayor resistencia se espera un mayor intervalo. Conviene aclarar que en los diagramas de Pareto presentados, el color negro indica un efecto negativo mientras que el blanco representa un efecto positivo.

La variable que más afecta el intervalo de tiempo característico (& Delta;θ) es el adsorbente, debido a la diferencia en sus isotermas [3]. Los menores intervalos característicos se encontraron en la zeolita 4A. Aunque en la zeolita se presenta mayor resistencia a la transferencia de masa, se favorece el potencial termodinámico que ocasiona la adsorción, lo que da lugar a una mayor velocidad de adsorción.

La asimetría (Ψ), cuyo diagrama de Pareto se muestra en la figura 6, para todas las simulaciones fue superior a 1; esto indica que la velocidad de adsorción disminuye al aumentar la carga adsorbida, lo que se atribuye a la reducción de la fuerza motriz a medida que el sistema se aproxima a la condición de saturación. Los frentes simétricos se presentan únicamente en casos isotérmicos con isotermas altamente no lineales y grandes efectos térmicos. El factor más influyente en la asimetría de la curva de ruptura es la liberación de calor [11] ya que, una vez comienza la adsorción, el enfriamiento del lecho es un proceso lento y el incremento de temperatura disminuye la capacidad de retención del lecho; esto respalda la consideración de que la variable dominante es el coeficiente de transferencia de calor.

La temperatura máxima es directamente proporcional al mecanismo utilizado para refrigerar el lecho, como se aprecia en la figura 7. El máximo cambio de temperatura fue de 87K, correspondiente al ensayo donde se usó la zeolita 4A con la alimentación de mayor humedad. En general, la zeolita presenta mayores cambios de temperatura, atribuibles a una mayor velocidad de adsorción, si se tiene en cuenta que el calor de adsorción es similar al de la sílica gel. Anteriores investigaciones de efectos térmicos en la adsorción de agua en zeolitas [18] encontraron que el contenido de humedad es la variable que ejerce mayor influencia sobre la temperatura máxima; se han hallado incrementos de temperatura entre 50 y 80K, valores que concuerdan con el máximo cambio encontrado en este trabajo. En el estudio mencionado solamente se analizó la adsorción en zeolita y no se realizaron cambios en las condiciones de remoción de calor, lo cual explica por qué en el presente estudio el contenido de humedad aparece en tercer lugar, después del coeficiente de transferencia y el tipo de adsorbente.

En la simulación de los 32 casos, la mayor caída de presión fue de 9,7kPa/m, con la zeolita como adsorbente. La ecuación de Ergun indica que el efecto mostrado en la figura 8 es ocasionado por la leve diferencia en las porosidades. Aunque ambos adsorbentes tienen el mismo diámetro equivalente, la distribución de tamaño de partícula puede favorecer una mayor porosidad en la sílica gel, lo que disminuye las restricciones al flujo y genera menores caídas de presión.

Es interesante notar que la presión aparece únicamente como factor importante en la caída de presión. Anteriores estudios [11], en los que se ha analizado el efecto de la presión en un intervalo más amplio (2-7atm), indican que la presión afecta la cinética cuando el mecanismo controlante es la difusión molecular en macroporos y en la capa límite de las partículas; sin embargo en este estudio el modelo cinético solo depende de la temperatura, como se espera de la difusión intrapartícula. A pesar de que existan diferentes regímenes que afecten el aspecto cinético, la forma de la isoterma es la que determina en gran medida la forma de la curva de ruptura. [3], lo cual justifica que para las cuatro variables evaluadas el adsorbente siempre fue un factor determinante.

A continuación se muestran los perfiles para el ensayo 0111, tanto para la zeolita como para la sílica gel. El perfil de composición muestra cómo se desarrolla la asimetría. La influencia del adsorbente es notable, según se corrobora al observar una menor dispersión para la zeolita, atribuida a la forma de la isoterma [2]. Datos experimentales y simulaciones [5] han mostrado que al volverse menos favorable la isoterma, las curvas de ruptura tienden a dispersarse, resultado que concuerda con el encontrado para la sílica gel cuya isoterma es menos favorable comparada con la de la zeolita. La pendiente de la curva de ruptura es proporcional a la velocidad de adsorción y es mayor cuanto más cerca se encuentren las curvas de nivel [11]. En la figura 9 se aprecia por qué la velocidad de adsorción es mayor en la zeolita.

En la figura 10 se presenta el perfil de carga adsorbida. Para la zeolita se observa la formación de dos zonas: la primera se genera por la penetración convectiva del flujo alimentado y en la segunda se percibe un frente característico de la curvas de ruptura. Para la sílica gel, debido a la dispersión del perfil, se observa una única zona. Se realizaron simulaciones ajustando el calor de adsorción a cero, para considerar una operación isotérmica y se observó el mismo comportamiento, lo que indica que este fenómeno no se debe al incremento de la temperatura, sino que es inherente al mecanismo de adsorción y a la convección.

Los efectos térmicos generan perfiles característicos de temperatura, como los mostrados en la figura 11. Las mayores temperaturas se alcanzan en los lugares donde inicialmente se desarrolla la adsorción. Las curvas de nivel de temperatura siguen un patrón semejante al de la carga adsorbida, lo que prueba la gran dependencia entre temperatura y velocidad de adsorción

Aunque el modelo incluye la variación de la velocidad superficial, los resultados indican que sólo cuando se presentan grandes gradientes de temperatura y altas humedades, la velocidad varía de forma apreciable. Para el ensayo con la máxima diferencia de temperatura, la velocidad más elevada fue un 14% mayor que la velocidad de alimentación y para el ensayo con la mayor humedad absoluta la mínima velocidad fue un 22% menor que la velocidad de alimentación. Para la velocidad de alimentación, la desviación de la velocidad mínima promedio para todos los ensayos es de 7%, mientras que la desviación de la máxima velocidad promedio es de 5%. Con esta información se verificó la aproximación de uso común en sistemas diluidos en los que se omite la variación de velocidad [3].

Conclusiones

En el presente trabajo se realizó el modelado de un lecho de adsorción incorporando efectos térmicos, dispersión axial, caída de presión y variación de velocidad para la deshidratación de una corriente de aire. Se utilizaron como adsorbentes y se compararon una zeolita 4A y una sílica gel 'A'. Los efectos de la distribución del tamaño de poro son fácilmente observables en la forma de la isoterma y en el coeficiente de transferencia de masa. A pesar de tener una menor capacidad final de adsorción de agua y un menor coeficiente de transferencia, la zeolita 4A presenta mayor velocidad de adsorción, comportamiento debido a la manera en que la isoterma favorece el potencial de adsorción. Tanto para la zeolita como para la sílica gel se pueden generar grandes cambios de temperatura en lechos adiabáticos, lo que da lugar a la disminución de la eficiencia de adsorción y el desgaste de las partículas.

Para las condiciones estudiadas, la variación promedio de velocidad no fue superior a 8%; en consecuencia, para condiciones semejantes a las evaluadas puede ser recomendable el desarrollo de un modelo que no considere la variación de velocidad, con el propósito de reducir el tiempo de cálculo.

A partir del modelo desarrollado, es posible elegir con anticipación el adsorbente, con el fin de optimizar y reducir los estudios piloto y realizar una interpretación de los resultados a partir de interacciones físicas reales.

Agradecimientos

Este trabajo fue desarrollado con el apoyo y financiamiento de Colciencias a través del proyecto: ''Síntesis y caracterización de zeolita LTA para el desarrollo y evaluación de un tamiz molecular para la deshidratación de etanol''; código 110152128366.

Referencias

1. M. Simo, C. Brown, V. Hlavacek. ''Simulation of Presure Swing Adsorption in Fuel Ethanol Production Process''. Comput. Chem. Eng. Vol. 32. 2008. pp. 1635-1649.         [ Links ]

2. D. Ruthven. Principies of Adsorption and Adsorption Processes. 1^st ed. Ed. John Wiley & Sons, Inc. New York, USA. 1984. pp. 1-433.         [ Links ]

3. D. Ruthven, S. Farooq, K. Knaebel. Pressure Swing Adsorption. 1^st ed. Ed. VCH Publishers, Inc. New York, USA. 1994. pp. 1-352.         [ Links ]

4. M. LeVan, G. Carta, C. Yon. ''Adsorption and Ion Exchange''. R. Perry, D. Green. (editors). Perry's Chemical Engineers' Handbook. 7^a ed. Ed. McGraw- Hill. New York, USA. 1997. pp. 1-66.         [ Links ]

5. A. Ribeiro, T. Sauer, C. Grande, R. Moreira, J. Loureiro, A. Rodrigues. ''Adsorption Equilibrium and Kinetics of Water Vapor on Different Adsorbents'' Ind. Eng. Chem. Res. Vol. 47. 2008. pp. 7019-7026.         [ Links ]

6. X. Wang, H. Chua. ''Two Bed Silica Gel -Water adsorption chillers: An effectual lumped parameter model''. Int. J. Refrigeration. Vol. 30. 2007. pp. 1417-1426.         [ Links ]

7. A. Gorbach, M. Stegmaier, G. Eigenberger. ''Measurement and Modeling of Water Vapor Adsorption on Zeolite 4A-Equilibria and Kinetics''. Adsorption. Vol. 10. 2004. pp. 29-46.         [ Links ]

8. M. Gholami, M. Talaie. ''Investigation of Simplifying Assumptions in Mathematical Modeling of Natural Gas Dehydration Using Adsorption Process and Introduction of a New Accurate LDF Model''. Ind. Eng. Chem. Res. Vol. 49. 2010. pp. 838-846.         [ Links ]

9. X. Wang, W. Zimmermann, K. Ng, A. Charraboty, J. Keller. ''Investigation on the isotherm of silica gel+water systems TG and volumetric methods''. J. Therm. Anal. Calorim. Vol. 76. 2004. pp. 659-669.         [ Links ]

10. I. Park, K. Knaebel. ''Adsorption breakthrough behavior: Unusual effects and possible causes''. AIChE J. Vol. 38. 1992. pp. 660-670.         [ Links ]

11. M. Simo, S. Sivashanmugam, C. Brown, V. Hlavacek. ''Adsorption/Desorption of Water and Ethanol on 3A Zeolite in Near-Adiabatic Fixed Bed''. Ind. Eng. Chem. Res. Vol. 48. 2009. pp. 9247-9260.         [ Links ]

12. R. Yang. Adsorbents: Fundamentals and applications. 1^st ed. Ed. John Wiley & Sons, Inc. New Jersey, USA. 2003. pp. 1-410.         [ Links ]

13. J. Seader, J. Siirola, S. Barnicki. ''Distillation''. R. Perry, D. Green. (editores). Perry's Chemical Engineers'Handbook. 7^a ed. Ed. McGraw-Hill. New York, USA. 1997. pp. 1-108.         [ Links ]

14. S. Sircar, J. Hufton. ''Why Does the Linear Driving Force Model for Adsorption Kinetics Work?''. Adsorption. Vol. 6. 2000. pp. 137-147.         [ Links ]

15. D. Lide. CRCH andbook of Chemistry andPhysics. 90^a ed. Ed. CRC Press/Taylor and Francis. Boca Raton, USA. 2010. Version CD-ROM.         [ Links ]

16. Y. Liu, J. Delgado, J. Ritter. ''Comparison of Finite Difference Techniques for Simulating Pressure Swing Adsorption''. Adsorption. Vol. 4. 1998. pp. 337-344.         [ Links ]

17. W. Schiesser. The numerical Method of Lines. 1^st ed. Ed. Academic Press. San Diego, USA. 1991. pp. 1-326.         [ Links ]

18. M. Gwadera, K. Kupiec, J. Rakoczy. ''Investigation of Thermal Effects of Water Vapor Adsorption on Zeolites''. Technical transactions: Mechanics. Vol. 109. 2012. pp. 87-94.         [ Links ]